候选基因关联研究的统计分析方法*

哈尔滨医科大学卫生统计学教研室(150081) 肖 纯 史晓雯 刘芸良 张 奇 刘 艳

候选基因关联研究的统计分析方法*

哈尔滨医科大学卫生统计学教研室(150081) 肖 纯 史晓雯 刘芸良 张 奇 刘 艳△

随着新一代测序技术的发展及全基因组关联研究(genome-wide association study,GWAS)策略的推广，复杂性疾病基因关联研究涉及的SNP位点逐渐增加[1]，且资料收集的逐渐完善促使描述疾病结局相关的指标增多，使样本信息多元化[2]。

所谓候选基因关联研究是根据已有的生理、生化背景知识或现有的研究结果(例如连锁分析的结果或表达产物的功能)提示某段基因序列的变异可能与表型的变异有关来确定待研究的基因，也就是候选基因[3]。假设所选基因本身就是影响表型变异的主基因，同时借助基因扩增等实验技术，采用病例对照设计方法来比较病例组与对照组候选基因的组间差异，以此来确定候选基因与表型变异是否存在关联[4]，有利于探索复杂性疾病的致病基因，样本易收集且能检出基因的主效应及微效基因的作用[5-6]。目前针对候选基因关联研究的统计分析方法主要分为疾病结局由多个指标共同描述和SNP位点数目较多这两种数据类型[7]，本文对这两种数据类型的主要分析方法进行回顾，并对其中较为高效的分析方法进行详细介绍。

多指标数据分析方法

针对多指标数据的统计分析方法主要区别在于对各指标间相关性的校正方法不同，实际数据操作中应根据研究目的、专业背景知识及数据的分布类型来选择适当的统计分析方法。

1.传统分析方法

传统分析方法通常是采用回归模型对疾病结局与相关变量进行分析，以研究对象是否患病作为应变量，以位点的基因型和需要调整的混杂因素作为自变量进行分析，并且可以估计基因之间及基因与环境之间的交互作用[8-10]。但当疾病结局并非由单一指标来描述时，模型中的应变量就不再是是否患病，而是一些彼此相关的多个指标，采用回归模型就需将多指标信息缩减为一个综合得分，在损失数据信息的同时也降低了检验功效[11-12]。

2.TATES法

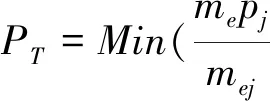
Sluis等人[13]同时指出当校正了各指标间的相关性后，在0.05检验水准下其检验效能是传统方法(即回归模型)的2.5～9.0倍，是多元方差分析的1.5～2.0倍。TATES法可通过PLINK、Mach2.dat/qtl、SNPtest和Gen/ProbABLE软件实现，同时兼具高效、人群分层校正的优势。

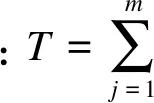
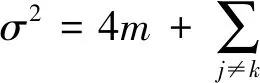
改良Fisher合并统计量可以通过R软件中fCopulae包实现，运行速度较快。Yang等通过一组模拟实验证实改良Fisher合并统计量方法对表型变量具有相关性的数据具有较高的检验效能，并有效地控制了Ⅰ类错误。Yang等同时将该方法应用于酒精滥用的遗传学研究。

此外，多元方差分析[16-17]通过基因型内与基因型间变异的协方差矩阵来计算表型变量的平均值的大小。将多个表形向量看作一个整体，从表形向量的任意线性组合中发现不同总体的最大组间差异，即基因位点对多个表型变量整体的影响。多元方差分析对于最小等位基因频率较大且指标间呈负相关的资料效能较高。另外，主成分分析可用于降低变量维度，同时可提高检验效能[18-19]。当疾病表型相关程度较高时，采用主成分分析得到的第一个主成分包含最多的表型信息(VarZ1≥VarZ2…≥VarZm)，故在基因关联研究中检验第一个主成分与SNP位点间的关系是将众多相关指标转化为较少几个成分的一种常用且有效的方法。但如何确定合适的主成分个数以及对抽象主成分的实际意义做出合理解释则成为该方法的难点[20]。

多位点数据分析方法

随着全基因组关联研究技术的发展成熟，一些疾病的基因组关联分析会产生几十个甚至是上百个的SNP位点，采用传统方法对这种多位点数据进行分析时，会受到维度的限制(即使三个基因位点也很难解释其交互作用)和单基因作用效果较弱的问题[21-23]。若每次仅分析一个或几个位点与疾病的关联，因检验效能较低常获得阴性结果，同时也带来了多重检验的校正问题[24]。

1.传统分析方法

传统的参数模型通常采用χ2检验或回归模型进行关联分析。基于χ2检验的关联分析方法原理是比较病例组与对照组某一等位基因频率是否有差异，若结果呈阳性，可提示该基因与变异相关，但基于χ2检验的关联分析并没有综合考虑到家族聚集因素和其他环境因素的共同作用[25-26]。

当前的候选基因研究中通常产生包含几十甚至上百个SNP位点的数据，采用传统的回归模型进行分析时也陷入了困境。第一，众多的位点信息导致模型中需要估计的参数增加，同时也导致了参数估计结果存在偏倚；第二，复杂性疾病是受多个基因的共同影响，每个基因的效应都较弱，采用回归模型进行筛选时，在分析交互作用之前需要存在一个主效应，复杂性疾病的各基因并不存在明显的主效应；第三，回归模型通常是在各种假定的遗传方式(显性遗传、隐形遗传、加性遗传等)下对各基因型进行了评分量化，然而这种量化具有不确定性或推测的特点[27]。

2.核心关联分析法(kernel association analysis)

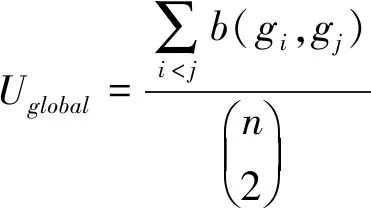
3.混合潜变量模型(latent variable modeling)

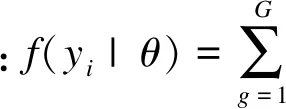
此外，机器学习方法(如多因子降维、分类回归树、随机森林等)也可以解决传统参数模型中的维度灾难问题。例如，多因子降维法(MDR)可减小因数据划分的偶然性引起的I类错误同时弥补了传统参数模型分析高阶交互作用时的缺陷，但是当测试集的病例对照比与整个数据集相近时会增加假阳性率[39]；分类回归树(CART)以二叉决策树的形式构建预测准则，容易理解、解释和使用，但当样本数据有小幅度变动时，构建的树就有较大变动，导致结果不稳定[40]。

[1]顾星博,李昂,温琪,等.Rstudio和随机丛林在高维全基因组学数据分析中的应用.中国卫生统计,2015,32(6):955-962.

[2]韩建文,张学军.全基因组关联研究现状.遗传,2011,33(1):25-35.

[3]Zondervan KT,Cardon LR.Designing candidate gene and genome-wide case-control association studies.Nat Protoc,2007,2(10):2492-2501.

[4]严卫丽.复杂疾病关联研究中的若干问题.遗传学报,2004,31(5):533-537.

[5]Tabor HK,Risch NJ,Myers RM.Candidate-gene approaches for studying complex genetic traits:practical considerations.Nat Rev Genet,2002,3(5):391-397.

[6]Johnson T.Bayesian method for gene detection and mapping,using a case and control design and DNA pooling.Biostatistics,2007,8(3):546-565.

[7]张学军.复杂疾病的遗传学研究策略.安徽医科大学学报,2007,42(3):237-240.

[8]葛锐,潘发明,夏果,等.强直性脊柱炎FcRL基因与环境暴露因素交互作用研究.中国卫生统计,2011,28(6):617-619.

[9]陈军,段炼,伍亚舟,等.直肠癌相关基因多态性及环境因素的影响因素分析.中国卫生统计,2012,29(1):31-33.

[10]张镏琢,秦平,李昂,等.不同人群的SNPs基因型数据中r2值对TagSNP数量的影响.中国卫生统计,2012,33(3):367-368.

[11]Paterson AD,Waggott D,Boright AP,et al.A genome-wide association study identifies a novel major locus for glycemic control in type 1 diabetes,as measured by both A1C and glucose.Diabetes,2010,59(2):539-549.

[12]Sung Y,Feng Z,Subedi S.A genome-wide association study of multiple longitudinal traits with related subjects.Stat(Int Stat Inst),2016,5(1):22-44.

[13]van der Sluis S,Posthuma D,Dolan CV.TATES:efficient multivariate genotype-phenotype analysis for genome-wide association studies.PLoS Genet,2013,9(1):e1003235.

[14]Li Q,Hu J,Ding J,et al.Fisher′s method of combining dependent statistics using generalizations of the gamma distribution with applications to genetic pleiotropic associations.Biostatistics,2014,15(2):284-295.

[15]Yang JJ,Li J,Williams LK,et al.An efficient genome-wide association test for multivariate phenotypes based on the Fisher combination function.BMC Bioinformatics,2016,17:19.

[16]Solovieff N,Cotsapas C,Lee PH,et al.Pleiotropy in complex traits:challenges and strategies.Nat Rev Genet,2013,14(7):483-495.

[17]王苗苗.双因素方差分析模型的构建及应用.统计与决策,2015,(18):72-75.

[18]Mei H,Chen W,Dellinger A,et al.Principal-component-based multivariate regression for genetic association studies of metabolic syndrome components.BMC Genet,2010,11:100-112.

[19]陈玉柱,方志峰,唐振柱,等.基于主成分回归分析的尿酸与相关影响因素研究.中国卫生统计,2016,33(3):382-388.

[20]Zhang F,Guo X,Wu S,et al.Genome-wide pathway association studies of multiple correlated quantitative phenotypes using principle component analyses.PLoS One,2012,7(12):e53320.

[21]Schaid DJ,McDonnell SK,Hebbring SJ,et al.Nonparametric tests of association of multiple genes with human disease.Am J Hum Genet,2005,76(5):780-793.

[22]李彪,陈润生.复杂疾病关联分析进展.中国医学科学院学报,2006,28(2):271-277.

[23]王璟涛,侯艳,李康.高维组学变量筛选方法的稳定性评价方法及应用.中国卫生统计,2016,33(3):374-378.

[24]金如锋,夏昭林.病例对照设计为基础的候选基因关联研究中交互作用的统计方法进展.复旦学报(医学版),2011,38(3):265-270.

[25]邹莉玲,赵耐青,秦国友,等.应用关联规则筛选疾病相关的SNP位点及其组合的分析方法.中国卫生统计,2009,6(3):226-233.

[26]李鹏飞,冯靖宇,严滢滢,等.胃癌易感基因筛选及多基因危险度分析.环境与职业医学,2011,28(9):531-534.

[27]陈峰,柏建岭,赵杨,等.全基因组关联研究中的统计分析方法.中华流行病学杂志,2011,32(4):400-404.

[28]Li H.U-statistics in genetic association studies.Hum Genet,2012,131(9):1395-1401.

[29]Wei Z,Li M,Rebbeck T,et al.U-statistics-based tests for multiple genes in genetic association studies.Ann Hum Genet,2008,72(6):821-833.

[30]Wu MC,Maity A,Lee S,et al.Kernel machine SNP-set testing under multiple candidate kernels.Genet Epidemiol,2013,37(3):267-275.

[31]李丽霞,郜艳晖,张敏,等.潜变量增长曲线模型及其应用.中国卫生统计,2012,29(5):713-716.

[32]武淑琴,张岩波.结构方程模型等同性检验及其在分组比较中的应用.中国卫生统计,2011,28(3):237-240.

[33]Dean N,Raftery AE.Latent Class Analysis Variable Selection.Ann Inst Stat Math,2010,62(1):11-35.

[34]Lee S,Jhun M,Lee EK,et al.Application of structural equation models to construct genetic networks using differentially expressed genes and single-nucleotide polymorphisms.BMC Proc,2007,1(Suppl 1):76.

[35]Tueller S,Lubke G.Evaluation of structural equation mixture models Parameter estimates and correct class assignment.Struct Equ Modeling,2010,17(2):165-192.

[36]Kelava A,Brandt H.A general non-linear multilevel structural equation mixture model.Front Psychol,2014,5:748.

[37]Berlin KS,Parra GR,Williams NA.An introduction to latent variable mixture modeling(part 2):longitudinal latent class growth analysis and growth mixture models.J Pediatr Psychol,2014,39(2):188-203.

[38]Tueller S,Lubke G.Evaluation of structural equation mixture models Parameter estimates and correct class assignment.Struct Equ Modeling,2010,17(2):165-192.

[39]华琳,郑卫英,刘红.基于优势比的多因子降维法在SNP交互分析中的应用.中国优生与遗传杂志,2008,16(11):938-947.

[40]梁茵.分类回归树算法的探讨.广东技术师范学院学报,2008,(6):29-32.

(责任编辑：郭海强)

国家自然科学基金(81172741;30972537)

△通信作者：刘艳，E-mail:liuyan@ems.hrbmu.edu.cn