基于Logistic回归惩罚函数的疾病诊断*
2017-03-09福建农林大学计算机与信息学院350002庄虹莉李立婷林雨婷温永仙
福建农林大学计算机与信息学院(350002) 庄虹莉 李立婷 林雨婷 温永仙
本文通过蒙特卡洛模拟方法产生模拟数据,分别得到训练集和测试集的分类精度,其中通过10折交叉验证算法选择训练集和测试集,分析比较传统的判别分析方法、SCAD-Logistic(简称SCAD-L)、Elastic net-Logistic(简称NET-L)、L2-Group MCP-Logistic(简称gMCP-L)和Group Bridge-Logistic(简称GB-L)的优劣。由于变量选择、参数估计和分类精度的结果受解释变量的类型、分组情况和样本量的影响,故本文分别设置了6组不同的模拟数据。
基于Logistic回归惩罚函数的疾病诊断*
福建农林大学计算机与信息学院(350002) 庄虹莉 李立婷 林雨婷 温永仙△
疾病诊断问题的实际是从高维的解释变量中筛选出比较重要的特征,辅助医疗人员进行疾病诊断,并且预测患者的危险状态,其本质也就是通过高维的解释变量进行分类的问题。已有大量学者将判别分析和Logistic回归应用到生物医学。比如田恒宇等[1]对胆总管结石的16种相关因素进行Logistic回归分析,建立相应的判别模型。然而随着时代的进步和高维数据的来临,传统的分类方法往往得不到预期的效果,国内大量的学者又对疾病诊断进行另一领域的研究。比如Inbarani等[2]基于粗糙集与粒子群优化相结合的方法,提出了用于疾病诊断关键特征识别的方法。梁丽军等[3]提出了结合弹性网和支持向量机算法的疾病诊断关键特征识别方法,该方法能够得到较高的分类精度。
由于大数据时代的来临,解释变量众多,变量之间复杂的关系[4],使得疾病诊断的传统方法失效。若改良后的方法能解决上述问题,则依然能够得到期望的结果。基于惩罚函数的变量选择方法能够有效的解决上述的问题,它主要有三类:单变量选择方法(SCAD等)、组变量选择方法(Group MCP等)和双层变量选择方法(Group Bridge等)。
本文比较[5]了基于Logistic模型的惩罚函数变量选择方法。利用惩罚函数实现变量选择和参数估计,通过十折交叉验证得到分类精度。通过不同类型数据的模拟,得到基于Logistic模型的Group Bridge具有优良的分类精度。
原理和方法
1.Logistic回归模型
对于普通Logistic回归模型,条件概率可表示为:
(1)
其中X=(X1,X2,…,Xn)T为设计矩阵,且Xj=(xj1,xj2,…,xjm)T,j=1,2,…,n,即X为n×m的解释变量;p=prob(y=1|X);y=(y1,y2,…,yn)T为响应变量,且yi(i=1,2,…,n)为离散二元变量,其取值为0或1;成功概率向量,p=(p1,p2,…,pn)T,pi是指取第i次观测值时因变量为1的概率;β0为截距,β=(β1,β2,…,βm)T为m维解释变量的系数向量。
在Logistic回归分析模型中,实现参数估计通常是通过最大似然法。最大似然法就是选取使得总体参数落在样本观察值邻域内概率达到最大的参数值作为其参数的估计值。Logistic回归模型的似然函数:
(2)
在似然函数的目标函数中加入各种惩罚项,就得到了各式各样基于惩罚函数的变量选择方法。
2.惩罚函数
惩罚函数的变量选择方法本质是将与解释变量不相关的解释变量所对应的系数向0压缩,主要分三类:单变量选择、组变量选择和双层变量选择。本文从中挑选了四种方法进行研究。
(1) SCAD-Logistic
SCAD是由Fan和Li[6]提出的一种在Lasso基础上发展的非凹的惩罚函数,是实现单个变量选择方法,将SCAD惩罚加载到Logistic模型中,就得到SCAD-Logistic。
(3)
其中pλ(|βj|)是SCAD的惩罚项,定义如下:
其中λ>0为罚参数,α>2为调整参数。Fan提出α=3.7时,估计效果最好。
(2)Elastic Net-Logistic

(4)
其中α为罚参数,当α=1时,上式为岭回归;当α=0时,上式为Lasso回归。所以说,Elastic Net回归结合了Lasso回归和岭回归的优点,既能消除自变量间的多重共线性,又能进行变量选择,以高预测精度选择稀疏模型,还能处理群组效应。
(3)L2-Group MCP-Logistic
当解释变量存在组结构时,我们希望对变量进行分组从而实现变量选择。L2-Group MCP是Huang和Breheny[8]提出的基于MCP的组变量选择方法,其组间的惩罚函数是MCP惩罚而组内的惩罚函数类似于岭回归,因此只能实现变量的组间选择而不能实现变量的组内选择。因此组变量的选择方法在于考虑了变量的分组情况,可以实现对同一组的变量同时保留或是同时删除。
假设已知分有J组变量,分别为A1,A2,…,AJ,每组的变量数为m1,m2,…,mJ。令βAj=(βj)j∈Aj是β相应变量构成的子向量,将Group MCP加载到Logistic模型中,就得到Group MCP-Logistic。
(5)

(4)GroupBridge-Logistic
双层变量选择方法的独特之处在于筛选变量时考虑了变量的分组结构,不仅能够实现筛选出重要分组,而且能够实现在组内筛选出重要的单个变量。Huang等[8]提出实现双层变量选择的其中一种方法是复合惩罚,即可以看成是组间惩罚和组内惩罚的一种复合函数,对第j组变量的惩罚项表示为:
其中Pouter是组间惩罚,Pinner为组内惩罚。
Breheny和Huang[9]提出,只需在组内和组间都选择单个变量选择的惩罚项,例如Lasso、SCAD、MCP惩罚等,就能实现组间和组内的变量选择。由此得到Group Bridge[10]变量选择方法,它是组间进行Bridge惩罚,组内进行Lasso惩罚。

(6)
其中,λ>0是罚参数,常数cj为βAj的调整参数,一般选择cj∝=|Aj|1-γ,γ为Bridge的指标,当0<γ<1时,可同时实现单变量和组变量的选择。
3.罚参数的选择
调整合适的罚参数对模型的求解至关重要,目标是使得模型的预测精度达到最优。本文通过10折交叉验证(10-fold Cross-Validation)实现罚参数的选择。10折交叉验证的流程详细见文献[11]。
模拟研究
本文通过蒙特卡洛模拟方法产生模拟数据,分别得到训练集和测试集的分类精度,其中通过10折交叉验证算法选择训练集和测试集,分析比较传统的判别分析方法、SCAD-Logistic(简称SCAD-L)、Elastic net-Logistic(简称NET-L)、L2-Group MCP-Logistic(简称gMCP-L)和Group Bridge-Logistic(简称GB-L)的优劣。由于变量选择、参数估计和分类精度的结果受解释变量的类型、分组情况和样本量的影响,故本文分别设置了6组不同的模拟数据。
1.模拟数据
假设数值分析的模型为:

模拟1:取Xi~N(0,1)且变量Xi和Xj之间的相关系数为Rij=0.1|i-j|,即变量之间存在弱相关关系且内部不存在组结构的数据,其中设定300个解释变量对应的参数(8个显著变量)为:
β300×1=(-2,1,1,0.5,-1,1,2,3.5,0,0,…,0)T
模拟2和模拟3仅是将解释变量之间的R0相关系数分别取值为0.5和0.8,使得解释变量之间存在相关关系和强相关关系,其他与模拟1保持相同的设置。
模拟4:在模拟1的基础上,加入了变量之间的多重共线性关系,使得:X1=2X2+4X3+2X4。
模拟5:考虑解释变量之间存在组结构、变量之间的多重共线性关系,且显著变量组内没有零系数。这里模仿Wei和Huang[12]的方法给出。将变量分成60组,此时有X=(X1,X2,…,X60),其中Xi=(X5(i-1)+1,…,X5(i-1)+5),1≤i≤60即每组有5个变量。详细的产生步骤见文献。其中每组参数的系数为(10个显著变量):β1=(0.5,1,1.5,2,2.5)T,β2=(2,2,2,2,2)T,β3=…=β60=(0,0,0,0,0)T
模拟6:与模拟5不同的是变量之间的具体分组不一样,且显著变量的组内存在零系数。数据的产生与模拟数据5类似,不同的是将解释变量分成74组,前四组大小为5,后70组大小为4(15个显著变量),即
β1=(-3,-2,-1,1,2)T,β2=(-3,-2,-1,1,0)T,β3=β4=(0,0,0,0,0)T
β5=(2,-2,1,1.5)T,β6=(-1.5,1.5,0,0)T,β7=…=β74=(0,0,0,0)T
通过计算机分别模拟这6种不同的数据类型,样本容量分别取n=1000,500,200,每种样本容量下重复500次实验。分别用传统的Fisher判别分析、SCAD-L方法、ENT-L方法、gMCP-L方法和GB-L方法对模拟数据进行变量选择和参数估计,并且得到训练集和测试集的分类精度。主要借助R语言中的glmnet包(ENT-L)、ncvreg包(SCAD-L)和grpreg包(gMCP-L和GB-L)实现变量选择和参数估计,进一步借助MATLAB得到训练集和测试集的分类精度。
2.模拟结果分析
根据数据模拟方法得到不同的数据类型,对其分别进行分析。由表1可以得出结论:

表1 解释变量之间存在各种相关且无组结构(模拟1到模拟4)的分析结果
*:表中“0”表示将全部样本y值为0的样本判断正确的精度,即对“0”的预测精度;表中“1”表示将全部样本y值为1的样本判断正确的精度,即对“1”的预测精度;表中“总体”表示将全部样本判断正确的精度,即对“总体”的预测精度;表中“多重共线性”表示解释变量之间存在多重共线性且无组结构;表中“训练集”表示将训练集中的全部样本判断正确的精度;表中“测试集”表示将测试集中的全部样本判断正确的精度;表中“变量数”表示选择的变量数量,Fisher不能实现变量的选择,因此用“-”表示。
(1)无论解释变量之间的相关程度如何,所有的判别方法都是随着样本量的减少分类精度随之变差,尤其 Fisher判别最为明显,当n (2)针对Fisher判别,当解释变量存在相关关系时,其在训练集的分类精度是最高的,但是在测试集的分类精度是最低的,而疾病诊断则是对患者进行疾病判别,因此该方法不适用;且当解释变量存在多重共线性时,无论样本量为多少,其测试集和训练集的分类精度下降为60%左右,导致方法失效。 (3)针对SCAD-L,随着解释变量之间的相关程度的加强,分类精度明显提高。在弱相关下SCAD-L的分类精度最高,但是在多重共线性下,分类精度不如其他的三种惩罚方法。 (4)针对NET-L,与SCAD-L相似,分类精度随着解释变量之间相关程度的增加而提高,甚至比SCAD-L高,主要是因为ENT-L适用于高度相关的变量选择方法。 (5)针对gMCP-L,是组变量选择,即只能实现变量的组间选择而不能实现变量的组内选择。这里是通过普通聚类的方法得到分组变量,得到的分类精度不稳定有可能是因为这里仅是通过普通的聚类方法实现变量的分组,聚类方法未使得变量准确的分组或是组变量存在零系数,从而影响分类精度。 (6)针对GB-L,是双层变量选择,即能够同时实现变量的组间选择和组内选择,因此相对于其他方法来说,均表现出优良的性质,具有最高或次高的分类精度和选择稳定且准确的变量数。 (7)综合以上的分析,无论是解释变量之间的相关程度、多重共线性,GB-L均表现出优良的性质,具有最高或次高的分类精度和选择稳定且准确的变量数。虽然在以上4种模拟中,gMCP-L在某些模拟下表现出优良的性质,但是它对解释变量聚类的准确率要求较高,稍有不慎可能使得精度骤然下降,因此在解释变量没有组结构或是不知具体分组的情况下,不建议使用gMCP-L。 当解释变量存在组结构时,由表2可以得出总体趋势与之前分析结果类似,存在差异的有以下几点: (1)当组内无零系数时,与模拟4相比,SCAD-L和NET-L分类精度明显降低,主要是因为SCAD-L是针对单个变量的选择方法,NET-L是针对高度相关的方法,并不适合解释变量存在组结构的数据类型。针对gMCP-L和GB-L,分类精度明显提高,因为此时的解释变量存在组结构,采用具有分组效果的惩罚方法优势更加明显;而gMCP-L的分类精度比GB-L高,可能是因为显著变量没有组内的零系数,这相对于组变量选择方法刚好可以完全选择出来,但对于双层变量选择的特点,极有可能将组内的显著变量中系数较小的变量剔除了,同时也可能将不显著变量组内的某些变量筛选出来。 (2)当组内存在零系数时,五种方法得到的分类精度比模拟5明显降低,因为数据更为复杂。针对组变量惩罚方法gMCP-L,仅当样本量逐渐减少的时候才出现比SCAD-L和NET-L分类精度高;与GB-L相比分类精度明显较低,而且选择的变量数较多,出现这个情况是因为gMCP-L只能进行组间变量选择不能进行组内变量选择,当组内存在零系数时,同一组中既存在显著变量又存在不显著变量,根据gMCP-L的特性会将一整组的变量选择出来,于是增加gMCP-L的误差,所选择的变量数也就增多或减少了。 3.小结 通过对6种不同数据类型模拟分析,无论是解释变量之间的相关程度、多重共线性、存在组变量或是组内是否有零系数,GB-L均表现出优良的性质,这主要是因为GB-L是双层变量选择,既能实现变量的组间选择又能实现组内选择,当变量无组结构或是组内有零系数时,并不会导致选择过多或过少的变量数,从而没有影响总体的分类精度;针对选择的变量数,GB-L较其他三种方法选择出更为准确的变量数;且在实际生活中,我们难以确认组内是否有零系数,因此我们可以考虑选择双层变量选择的方法,来保证各种数据类型的变量选择和参数估计的效果。 表2 解释变量之间存在组结构(模拟5和模拟6)的分析结果 *:表中“组结构且组内无零系数”表示解释变量存在组结构且显著变量没有组内零系数;表中“组结构且组内有零系数”表示解释变量存在组结构且显著变量有组内零系数。 本文采用了UCI 数据库中Arrhythmia 数据集进行实证分析,该数据集有452个样本,每个样本有279个属性,其中包括年龄、性别、心率、身高等。由于每个样本的第14个属性几乎都是缺失的,因此将这一属性剔除;接着查找每一个样本,只要有数据缺失就把该样本剔除。最后得到420个样本,278个属性。该数据集的属性维度较高,而每个类别的样本量又较少,有的甚至没有样本,因此将420个样本分为两类:心律失常病人和正常人,其中有183个心律失常的病人,并将此作为类别0 的数据集;237个正常人作为类别1的数据集。 1.五种方法的比较研究 表3 Arrhythmia 数据集实证分析结果 从表3可以看出,GB-L无论在训练集还是在测试集均保持最好的分类精度,其中测试集的分类精度达77.9%,针对选择的变量数:GB-L选择了12个变量。这里的gMCP-L精度低和选择的变量数多可能因为组内存在零系数。实证分析结果与模拟实验的结果大为相近,研究结果表明,GB-L方法的预测能力比其他模型高,具有有效的降维能力。 2.与其他方法的比较研究 梁丽军等[3]以UCI 中Arrhythmia 数据集为例进行测试,运用弹性网-SVM对疾病诊断进行关键特征识别,十折交叉验证得到分类精度为77.05%。而本文中的GB-L方法对疾病诊断进行关键特征识别的分类精度为77.9%,比弹性网-SVM的分类精度略好一点。由于本文也是通过十折交叉验证获取训练集和测试集,因此在相同条件下具有可比性。 1.GB-L方法具有较高的预测能力 本文从模拟和实证的角度系统地将GB-L方法与Fisher判别、Net-L、SCAD-L、弹性网-SVM进行比较。从结果上看,GB-L方法具有一定的优势,能提高分类精度,实现变量的选择。与模拟分析相比,GB-L预测精度下降了,因为实际数据比模拟数据有更加复杂的关系,而且重点影响总体预测精度的是对“0”预测,由于此时NET-L和gMCP-L对“0”具有较高的预测精度87.5%和78.3%均优于GB-L对“0”预测57.1%,但是由于从模拟分析结果中得知NET-L及其的不稳定性,因此考虑是否可以结合GB-L(对“1”的预测)和gMCP-L(对“0”的预测),从而提高总体的预测精度。 2.基于惩罚函数的变量选择方法的运用 目前,基于惩罚函数的变量选择方法在各个领域中被广泛运用。例如,方匡南等[13]提出在基于Lasso的Logistic模型上研究信用卡的违约问题;蒋士正等[14]提出Lasso和神经网络的组合模型来预测复杂路网短时交通流。因此,GB-L无论是对于疾病诊断问题,信用卡违约问题还是复杂路网短时交通流等问题都具有研究价值。GB-Logistic方法对于具有组效应的高维问题可以进行有效地处理,这对大数据时代下的高维数据处理奠定了基础。 [1]田恒宇,周汉新,鲍世韵,等.胆总管结石相关因素及指标的Logistic回归判别分析.中国普通外科杂志,2007,16(5):483-485. [2]Inbarani HH,Azar AT,Jothi G.Supervised hybrid feature selection based on PSO and rough sets for medical diagnosis.Computer methods and programs in biomedicine,2014,113(1):175-185. [3]梁丽军,刘子先,王化强.基于弹性网-SVM的疾病诊断关键特征识别.计算机应用研究,2015(5):1301-1304. [4]杨凯,侯艳,李康.条件推断森林在高维组学数据分析中的应用.中国卫生统计,2016,(2):215-218. [5]华洋静玲,洪金省,张海荣,等.三种方法构建鼻咽癌患者营养指数模型的比较分析及其截断点确定.中国卫生统计,2016,(2):194-197. [6]Fan J,Li R.Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties.Journal of the American Statistical Association,2001,96(456):1348-1360. [7]Hui Z,Trevor H.Regularization and variable selection via the elastic net.Journal of the Royal Statistical Society,2005,67(2):301-320. [8]Huang J,Breheny P,Ma S.A Selective Review of Group Selection in High-Dimensional Models.Statistical Science,2012,27(4):481-499. [9]Breheny P,Huang J.Penalized methods for bi-level variable selection.Statistics and its interface,2009,2(3):369-380. [10]Huang J,Ma S,Xie H,et al.A group bridge approach for variable selection.Biometrika,2009,96(2):339-355. [11]高少龙.几种变量选择方法的模拟研究和实证分析.山东大学,2014. [12]Wei F,Huang J.Consistent group selection in high-dimensional linear regression.Bernoulli:official journal of the Bernoulli Society for Mathematical Statistics and Probability,2010,16(4):1369-1384. [13]方匡南,章贵军,张惠颖.基于Lasso-logistic模型的个人信用风险预警方法.数量经济技术经济研究,2014(2):125-136. [14]蒋士正,许榕,陈启美.基于变量选择-神经网络模型的复杂路网短时交通流预测.上海交通大学学报,2015,49(2):281-286. (责任编辑:刘 壮) 国家自然科学基金项目(31171448);国家自然科学基金项目(31571558);福建农林大学数学建模实训室(111ZS1503) △通信作者:温永仙,E-mail:wenyx9681@fafu.edu.cn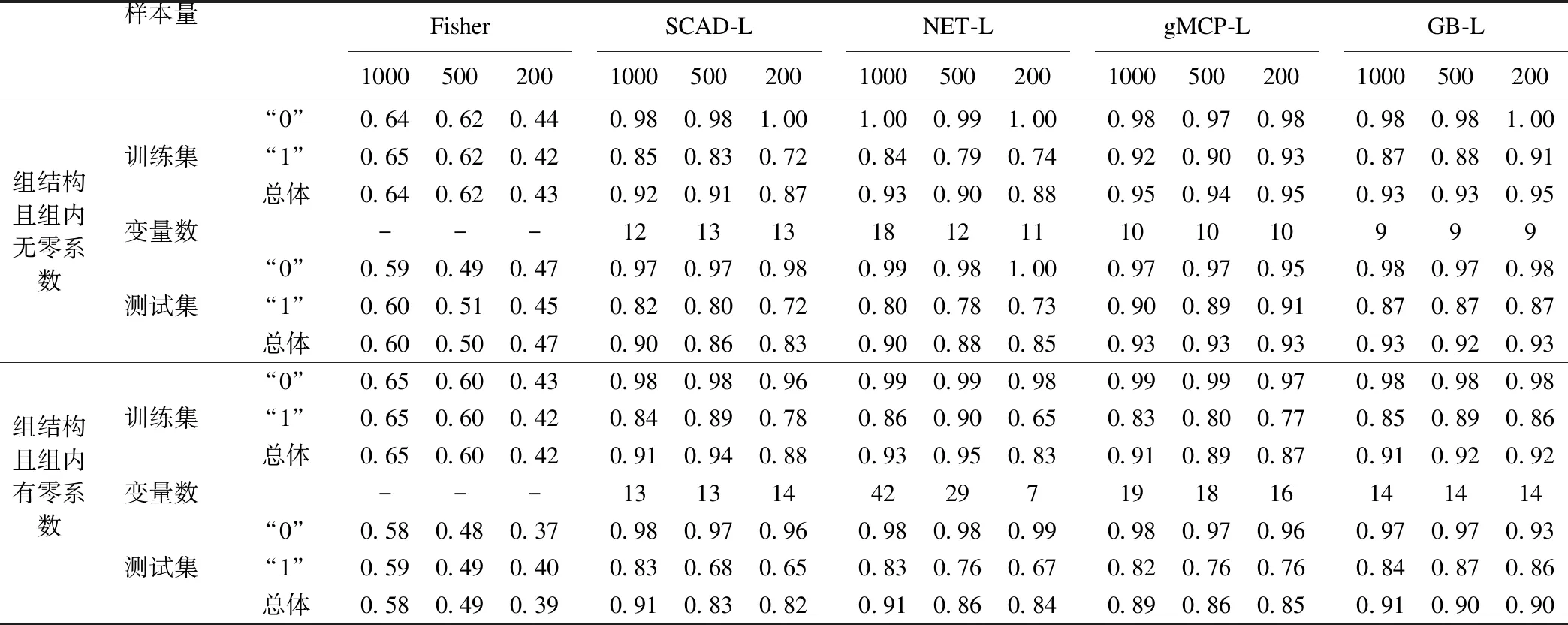
材料与对象
结果与分析
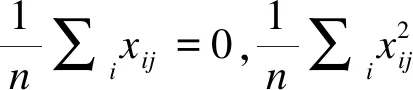

讨 论
