变式教学在高中数学教学中的应用探究

郭文娟

[摘 要] 变式教学作为一种有效的教学策略，在实践中被广泛应用并发挥着积极作用. 高中数学采取变式教学需要遵循几个基本原则，在遵循这些基本原则的基础上，其实际应用的形式应该是多样的，同时注意应用时所遇到的问题.

[关键词] 高中数学；变式教学；原则；应用；问题

所谓变式教学，主要指教师有计划地对相关命题进行转化，采取更换命题里面非本质特点、合理更换问题条件以及结论、有效转换题目内容以及形式的手段，正确引导学生了解数学对象所具有的本质属性，同时在这种变化过程中逐渐内化相关数学知识，找出数学规律.数学教师实施变式教学，可以有效提高学生自身学习主动性，引导学生站在不同角度上深入分析问题，从而增强对比不同问题的能力，强化学生自身数学思维意识. 本文在阐述高中数学教学过程中变式教学应该遵循的基本原则的基础上，结合高中数学教学中实践，总结了数学变式教学的几种课堂实施形式，希望可以为高中数学教学教师提供一定的参考.

高中数学采取变式教学需要遵循的原则

1. 暴露过程原则

教学过程中，数学教师应该使学生明晰整个数学思维过程，积极参与数学知识的发现过程，建立一种学生自己可以灵活应用的知识体系，从而增加其学习积极性并且强化其数学能力.

2. 启迪思维原则

教师需要谨慎合理地设计相关数学问题情境，熟练掌握变式教学，使其产生启发学生学习的效果，将问题当作教学出发点，指引学生快速发现问题，深入分析问题，并且正确解答问题. 教师应该对创设思维情境、合理设置一些思维阻碍或者是增加思维阶梯等手段进行充分的利用，从而将学生求知欲完全激发出来，提高学生求知欲，实现启迪学生思维这一教学目标.

3. 目标导向原则

教师应该依据教学内容以及教学大纲要求开展教学任务，变式教学实施过程中，课堂教学形式具有较高灵活性，然而教学内容必须切实可行，不仅要遵循目标导向原则合理设计课堂内容，还应该保证其实践性，对学生自身理解能力以及知识面程度进行考虑，所举教学案例或者是例题一定要符合实事求是的要求.

高中数学课堂教学中变式教学的实际应用

1. 知识概念的变式

高中生重点学习课程之一就是数学，学生想要进一步巩固数学基础，就应该准确理解并且熟练应用数学概念.数学教师一定要采取各种教学模式使教学达到课程标准，从而增强学生所具备的知识迁移能力. 对于传统教学来说，比较重视答题技巧的教育，教师在课堂上仅仅通读一下数学知识概念，再使学生采取死记硬背的方式对其进行识记，因而很多学生都没有充分了解数学知识概念，对学生课堂学习效果以及解题能力造成严重的影响. 教师对相关数学概念实施变式教学，能够引导学生深入了解概念内涵以及知识的外延，激发学生学习兴趣，改善课堂教学氛围.

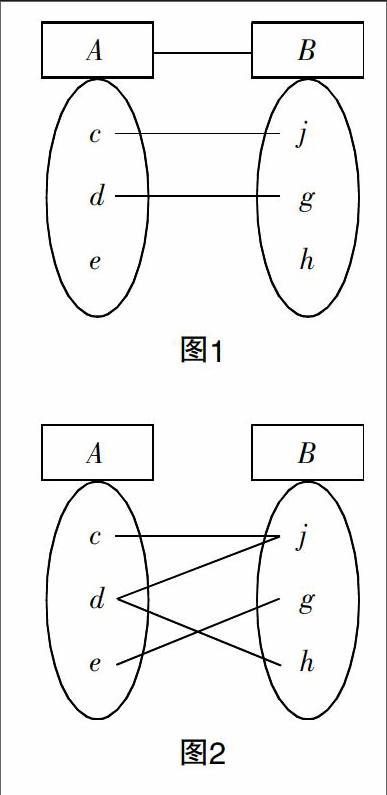
例如，教师在讲解苏教版高中数学第2章第3节“映射的概念”相关内容的时候，课本上映射概念主要指对于两个非空集合（比如A和B），依据存在法则f保证集合A里面所有元素在集合B里面均存在唯一确定元素与之相对应. 数学教师首先需要站在正面角度上通过图形对学生进行说明，再基于该初步理解的条件下，进行概念变式，有效引导学生按照图1以及图2对有没有映射进行判断.

其中图1集合A里面的元素在另一个集合B里面，没有对应元素，就是空对空的情况；而图2集合A里面的元素d在另一个集合B里面对应两个不同的元素，就是一对多的情况. 数学教师采取变换方式将映射的图形清楚表示出来，引导学生熟悉概念里面的关键词，比如“唯一确定”或者是“每个元素”，让学生知道怎样判断图1以及图2都与构成映射的相关条件不符. 该方式不仅可以让学生深入了解映射基本概念，同时还能够给解题训练做好准备，提高解题效率.

2. 习题变式

数学教师讲解理论知识的主要目的是为了让学生可以应用这些理论知识快速解答数学问题，从而提高学生的课堂学习效果. 由于高中数学课程内容具有很强逻辑性，大部分数学问题都比较抽象，所以教师教学时对相关问题进行变式，既可以让学生获取到解题方法，同时还能够循序渐进地逐步引导学生明晰解题思路，从而促进学生有效解决各种数学问题.

（1）变换题目条件或问题

数学教师通过变换题目里面的已知条件与最终答案或者是变换内容与题目形式的方式，能够让学生逐渐明晰题目的内涵，在整个变换环节掌握数学知识，同时探索题目所遵循的数学规律，以后遇到这类题目的时候能够做到快速解答问题. 例如教师在讲解苏教版高中数学选修2教材第2章《圆锥曲线与方程》里面“抛物线”相关内容的时候，对于题目：抛物线具体方程表达式为y2=4x，于该曲线上找出点M（x，y），保证其和原点之间的距离最短. 数学教师能够通过下列变式提高学生对这种问题的具体反应能力：

①抛物线具体方程表达式为y2=4x，于该曲线上找出点M（x，y），保证其与点A（a，0）之间的距离最短.

②知道抛物线具体方程表达式为y2=2px，于该曲线上找出点M（x，y），保证其和原点之间的距离最短.

再例如，教师在讲解苏教版高中数学必修1教材第2章《函数概念与基本初等函数》里面函数单调性相关内容的过程中，将“y=x2，其中x∈（0，+∞），对指定区域里面函数单调性进行判断”当作原型进行变式教学，其中也存在两种变式，分别是：

①y=x2，其中x∈（-∞，0），对这个时候函数单调性进行判断.

②教师可以把题目里面的定义域忽略，再有效引导学生完成探究过程，这时能够发现该函数已经没有单调性.

（2）变换题目具体解答方法

对于数学思维能力而言，非常关键的组成部分就包括发散思维，很多高中数学题目均融入了不同教学知识点，仅仅采用一种思维方式很难获得正确答案，所以教师通过变式教学引导学生对题目解答方法进行合理转换，从而提升学生发散思维的水平. 例如教师在讲解苏教版高中数学必修4教材第1章《三角函数》相关内容的时，有如下题目：tanx=，请问sinx以及cosx分别是多少.学生看到这一题的时候，能够想到tanx=以及sin2x+cos2x=1这两个三角函数，如果联立这两个不同的等式，然后依据题目给出的已知条件就可以发现sinx=，cosx=或sinx=-，cosx=-. 数学教师还能够引导学生依据图像对这一问题分不同情况讨论，由于tanx=，故讨论过程中能够把x置于第一象限或者是第三象限.

高中数学课堂教学中应用变式教学注意的问题

变式教学法主要指针对不同种类数学题目，利用表面形式变化手段，把其变换成另外一种学生比较熟悉的形式，让学生在这种多变换过程中体会到数学知识应用所具有的灵活性，同时也让学生感受到数学知识的魅力. 因此，高中数学教师进行课堂教学的过程中，合理有效地应用这种变式教学，既可以让学生深刻了解所获取的数学知识，同时还可以提升课堂教学氛围，使其更加活跃. 然而，若教师应用变式教学时没有合理把握变式难度和变式数量，就会让学生承受一定的心理压力，无法获得理想的教学效果.高中数学教师应该注意的问题主要有：

1. 变式难度应该适中，不宜偏难

对于高中数学教师而言，其在进行变式教学的时候，相关数学题目的变式既不可以过于简单，过于简单，达不到学习的效果；也不可以过于难，过于复杂，容易打消学生学习的积极性. 在进行变式教学的过程中，我们需要逐步提升难度.

2. 变式的数学题目不可以过多

若过多，就会让学生觉得非常广泛，从而无法准确把握住要点. 除此之外，太多数学变式解题将消耗很多课堂时间，对学生及时消化并且吸收教师传授的内容十分不利.

3. 重视与学生之间的配合

教师在课堂上讲解变式解题时，應该及时提出问题，和班上的学生进行互动，这样可以使课堂氛围更加活跃，同时也可以将学生兴趣有效激发出来，实现改善教学质量的目的.

总之，教师进行课堂教学时，有计划地合理应用变式教学，能够提升学生从不同角度分析并且解决问题的能力，进一步强化学生自身数学思维意识，并且活跃课堂教学范围，多角度发展高中学生思维，同时有效提升数学教学水平.