高考数学命题新特点审视
2017-03-09曹卫民
曹卫民

[摘 要] 高考试题一直在不断变革,在寻求创新. 从高考试题中,教师要进行研究、思考、挖掘,读懂试题背后隐藏的故事,才能有助于数学教学的开展.
[关键词] 高考;试题;本质;思想;变革;命题;编制
众所周知,高考变革牵动着数以万计的家庭,也给教师带来了教学变革的思考.从大量研究数据表明,近年来高考愈来愈走向对知识本质、能力、思想等角度的考查,这是一个新的发展方向.
从全国统考到分省命题,到2016年高考剩下仅仅七省市命题,可见高考命题也在不断发生变革. 南师大单教授,浙江大学金教授等高考命题专家都准确给出了近年来新高考发展的方向:数学知识考查必须脱离题型教学,必须脱离题海训练模式,让强化训练模式没有用武之地,让灵活教学、思维培养成为数学教学的主流.从教育部基础教育司联合清华、北大等名校对于各地高考数学试卷命题质量的调查研究报告指出,江苏、浙江等分省命题质量很好,也引导着新一轮教学改革的方向. 那么从这些优秀的高考试题中我们教师读懂了什么?给我们的教学点出了什么样的实施方向?让教师思考如何去改变自己的教学传统适应新高考?这些都是试题背后值得教师思考的方向.
读懂本质的重要性
高考中的双基问题是数学基本知识考查的第一层次,这一类问题对于学生而言相对容易,不在计算、记忆等环节出现错误则没有特别的失分现象. 但是,仅仅凭借基本知识和基本技能是无法对于学生认识能力进行区分的,这里以浙江等地的高考试题为例给出了数学基本知识考查的第二层次,即本质的深层次认知.
知识1:椭圆、双曲线、抛物线为何称之为圆锥曲线?
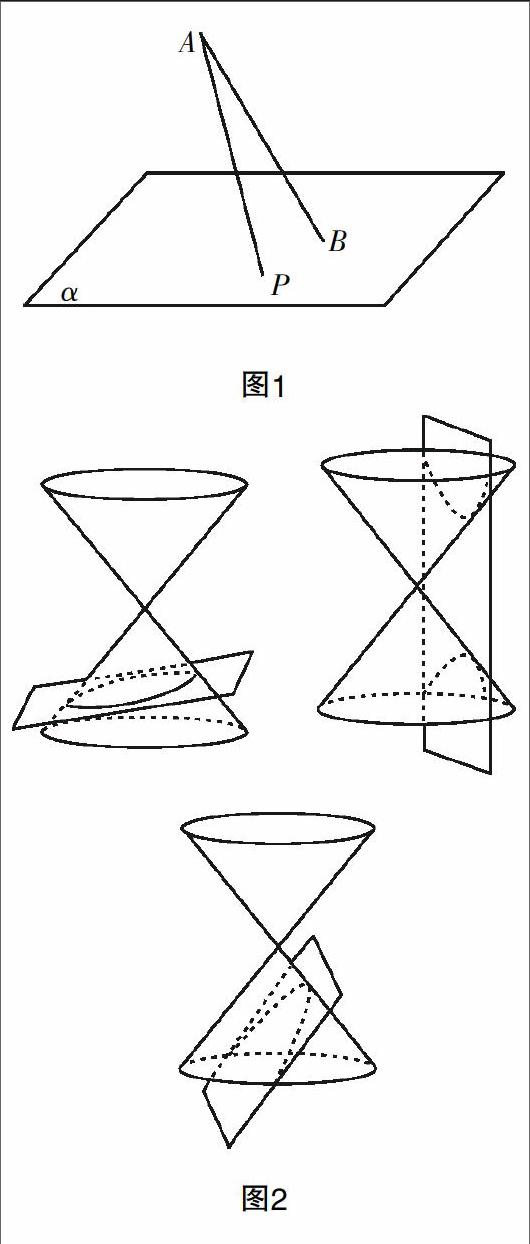
众所周知,圆锥曲线主要是研究椭圆、双曲线、抛物线,这三种曲线的概念在教材中也给出了介绍,动点到两定点距离和为定值的点的轨迹称之为椭圆(a>c),双曲线是到两定点距离差的绝对值为定值的点的轨迹(a 问题1:(2015年浙江文)如图1,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PAB=30°,则点P的轨迹是__________. (填写线段、圆、椭圆、双曲线、抛物线中的一种或多种) 分析:这是典型的圆锥曲线概念问题,但是其不同于教材中的第一定义,往往让学生极为费解.在教材章头图中有这样三幅图(图2),用与圆锥母线呈不同角度的平面去截圆锥,可以得到不同的截口曲线,这是椭圆、双曲线、抛物线,这是三者为何称之为圆锥曲线的主要原因. 显然,高考命题已经超越了教材基本的第一定义的考查,而延伸到了师生都不太关注的章头图大做文章. 上述问题也不难发现点P的轨迹是圆锥与平面α的截口曲线,考虑到一定的角度,最终是椭圆. 可以这么说,关注数学本质成为高考数学命题的重要特色,这在近些年很多经典问题中出现,给出下列问题供读者后续研究. 问题2:(2016年江苏)在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,·=4,·=-1,则·的值是_________.(答案:,向量极化恒等式) 问题3:(2015年浙江)对任意的x∈R,存在函数f(x)满足__________. (答案(3),函数概念) 说明:对于数学知识本质的深层次的思考,是新高考试题命制的一个重要方向,这种试题体现了新高考的重要导向作用,完全抛弃以训练为主导的题海模式,将训练效用降低到最低,从数学理解、知识掌握、本质感悟的角度来区分学生,这样的试题将会愈来愈多地体现在应试中,成为教师教学的优秀素材,也给师生的教与学提供了數学知识“灵魂”的认知. 理解知识的边缘性 作为教师,我们常常有这样的感受:今年的某些高考试题感觉超纲了,怎么可以这样解决?有些问题用一些边缘性的知识解决非常快速,但是好像平时用到比较少,是不是不应该考这样的问题?面对这样的问题,我们该如何选择教学?这里笔者借用单教授的一句话:只要是能用高中常规方法解决的问题,都不算是超纲的问题,至于是不是还有其他更为巧妙的方法,能不能用边缘性的知识解决?这都不是问题. 问题4:(2008年江苏)若AB=2,AC=BC,则S△ABC的最大值________. 问题5:(2013年江苏)在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4. 设圆的半径为1,圆心在l上. (1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围. 分析:上述两个问题的背景是一致的,利用了阿波罗尼斯圆,利用这一几何背景可以较为快速地建立模型、解决问题. 何为阿波罗尼斯圆?在平面上给定相异两点A,B,设P点在同一平面上且满足=λ,当λ>0,且λ≠1时,P点的轨迹是个圆,这个圆我们称作阿波罗尼斯圆. M,N分别为线段AB按定比λ分割的内分点和外分点,则MN为阿波罗尼斯圆的直径. 这一知识属于高考边缘性知识,掌握的话可以简捷运算过程,这对于优秀学生而言是一种不错的教学指导,是新高考命题呈现的特征——问题具备数学背景,多探究这样的数学背景有助于研究新一轮命题导向. 说明:经过大量研究发现,高考试题的编制往往蕴含深奥的知识背景,这些知识并不出现在中学数学教材中,但是在教学中加以一定的渗透,将有助于教师理解问题,引导我们进行合理的教学.如江苏卷极为喜欢的阿波罗尼斯圆,向量中的极化恒等式,不等式中的三角不等式等等,这些在中学数学教材中都是边缘性知识,但是却在应试中深受专家偏爱,仅仅从高考考查的角度来说,这是教师需要研究的方向,是从试题背后挖掘的重要信息. 关注思想的深刻性 数学思想是高考试题必然倚重的背景,特别对于一些具备区分学生层次的试题来说,其背后隐藏的数学思想具备着深刻性,从学生整体素养角度来说,具备数学思想并能灵活运用的学生,往往更受到顶尖大学的青睐,这也是数学思想为什么一直在高考问题命题中占据重要地位的原因.单教授在每年江苏卷评析中都会提到数学思想在中学数学教学中的缺失,正是因为这种缺失,导致学生问题的解决不能够转换角度,找到恰当的、巧妙的方式. 分析:本题的标准解答是利用参变分离结合分类讨论,笔者认为这并不是编题者真正的意图!显然,在这样的问题背后,我们更多的看到的是如何利用数形结合思想来处理零点问题,函数零点是代数中的概念,转换成几何的语言即是两个函数交点的横坐标,因此这才是思想方法在这样的问题解决中具备的足够魅力!不妨记g(x)=ax+b,h(x)= -x2,结合图4不难发现两个极端位置,因此可以轻松解决-3≤b≤9-4. 说明:思想方法一直是高考命题体现能力立意之处,也是体现学生间思维层次的重要标杆,以不同的思想方法衡量学生,这是新高考命题的重要特点,也成为教师教学需要渗透和改变的,将思想方法通过典型问题进行渗透,才能引导学生脱离训练模式,引导其通过认真的思考、潜心的感悟,去领略思想方法在解决数学问题中的巧妙性. 总之,新高考走在能力立意和思维考查的道路上,教师要领悟命题者在上述方面的转变,进而提高自身对于教学的转变和感悟,从较早的时间段入手引导学生做好数学知识本质的思考、思维的启迪、边缘性知识的开拓和思想方法的渗透,只有多方面的入手才能提高学生的数学能力.
