基于牛顿欧拉法的SCARA机器人动力学参数辨识*

张铁 梁骁翃 覃彬彬 刘晓刚

(1.华南理工大学 机械与汽车工程学院， 广东 广州 510640; 2.桂林航天工业学院 广西高校机器人与焊接重点实验室， 广西 桂林 541004)

SCARA机器人是一种具有选择性柔性的近似圆柱型工作空间的机器人.它水平面灵活度高、铅垂平面刚性好，广泛应用于分拣、装配和码垛等工作[1].工业应用中要求SCARA机器人具备高速、高精度的特性，即要求机器人具有精确的运动控制算法.运动控制算法离不开对机器人的动力学分析.为获得更精确的动力学方程，须对机器人动力学参数进行辨识[2].

国内外学者研究了不少动力学参数辨识方法，如解体实验测量法、CAD法、理论辨识法[3].Armstrong等[4]将PUMA560机器人解体后在专门设计的测量平台上进行惯性参数测量实验.解体实验测量方法的缺点在于需要专门实验装置，工作量大，且忽略了连杆关节特性的影响.王树新等[5]在不解体的情况下，采用CAD方法计算各动力学参数值，并基于动力学模型和单关节试验结果修正相应动力学参数.受限于机器人制造工艺精度，由CAD模型辨识得到的动力学参数并不能十分精确地对应机器人实际动力学模型.Chan[6]将动力学模型整理为一个上三角系数矩阵与动力学参数相乘的形式，提高了参数辨识算法效率.理论辨识法将机器人的动力方程表示为动力学参数的线性方程，虽然获得的参数多是组合值，但是参数辨识精度高[6- 10].

文中选用理论辨识法对SCARA机器人进行动力学参数辨识，辨识所得动力学参数将用于机器人动力学模型的更精确建模，并作为文中未涉及的后续机器人力控制算法研究的基础.

1 基于牛顿欧拉方程的SCARA机器人动力学建模

实验在国内某公司生产的SCARA机器人上进行.因第4轴旋转关节运动时对第3轴移动关节造成一定量同方向耦合，且考虑到第4轴运动对SCARA机器人主要的水平面定位运动不产生影响，为合理简化动力学方程，建模时将第3关节和第4关节合并，作为组合连杆3，关节类型为移动关节，并在实验时保持第4关节锁定.根据Craig方法建立SCARA机器人DH模型[11].图1为SCARA机器人的DH模型示意图.SCARA机器人连杆参数见表1.

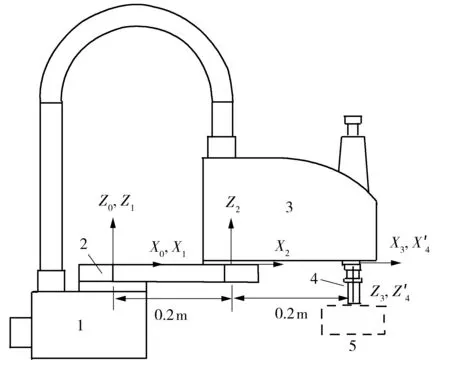
1—底座;2—连杆1;3—连杆2;4—组合连杆3;5—负载，虚线表示可装卸

iαi-1/(°)ai-1/mdiθi100.00θ1200.20θ231800.2d30

1)θ、α、a、d均为连杆参数，下标表示不同的连杆.

将表1参数代入式(1)可得相应的SCARA机器人齐次变换矩阵：

(1)

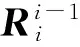
动力学分析的研究方法有很多，如牛顿欧拉方法、拉格朗日方法、旋量方法等[12- 13].牛顿欧拉方法是一种常用的机器人迭代动力学算法，它基于牛顿第二定律和欧拉方程，由两部分组成，具体计算步骤归纳如下[11].

牛顿欧拉方法的第1部分是从连杆1到连杆n向外迭代计算连杆的速度和加速度.

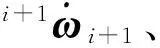
(2)

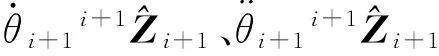
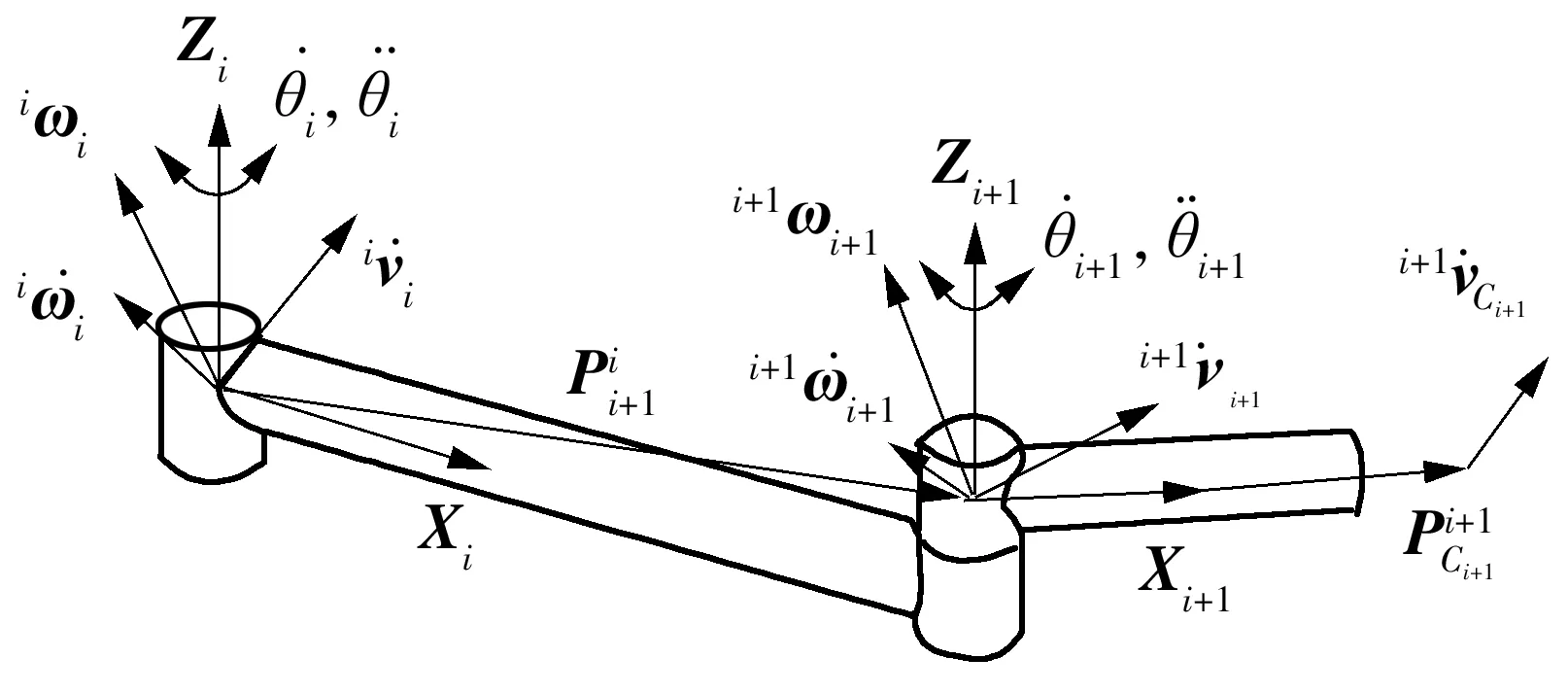
图2 旋转关节i+1的速度、加速度推导

Fig.2 Derivation of velocity and acceleration of revolute jointi+1

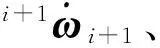
(3)

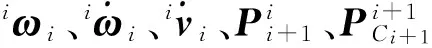
图3 移动关节i+1的速度、加速度推导

Fig.3 Derivation of velocity and acceleration of prismatic jointi+1

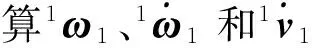
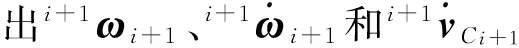
(4)

式中，Ci+1Ii+1为连杆i+1在质心坐标系{Ci+1}中的惯性张量.

重复运用式(2)-(4)，可计算出连杆1质心的惯性力1F1和力矩1N1，连杆2质心的惯性力2F2和力矩2N2，以及组合连杆3质心的惯性力3F3和力矩3N3.

牛顿欧拉方法的第2部分是从连杆n到连杆1向内迭代计算连杆间的相互作用力和力矩以及关节驱动力矩.

图4为单连杆的包括惯性力的力平衡示意图.按式(5)计算连杆j-1作用在连杆j上的力jfj和力矩jnj.

(5)

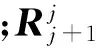
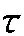
(6)

(7)

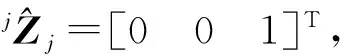
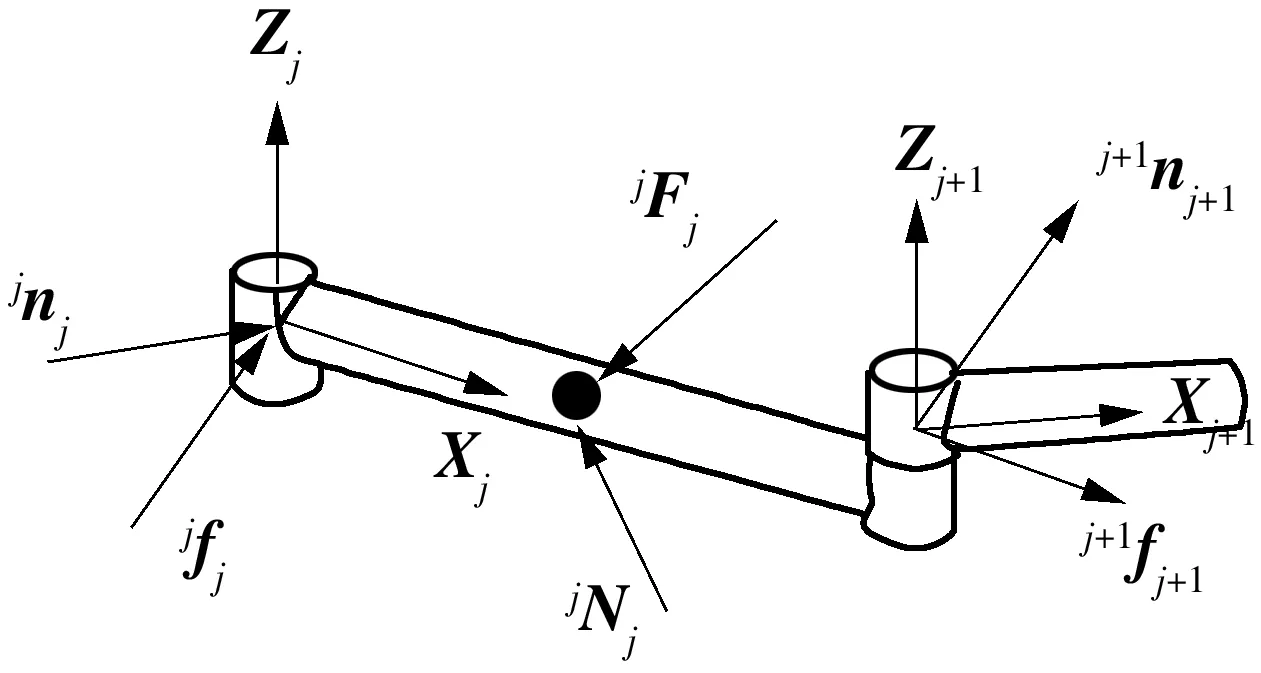
图4 单连杆的力平衡Fig.4 Force balance of a single link

关节电机提供的力矩中，除包含驱动关节运动的部分，还包含有克服摩擦力以及电机转子转动所需的附加力矩.对这部分力矩按式(8)建模[14]：

(8)

式中，Jmi为电机的转动惯量，fi1、fi2分别为库伦摩擦力系数和粘滞摩擦力系数.

结合由牛顿欧拉方程推导的关节驱动力矩和按式(8)建模的附加力矩，经合并化简，获得关节力矩关于一组动力学可辨识参数集的线性表达式.

进一步整理得末端不带负载时关节力矩表达式方程组的向量形式：

(9)

A为3×13系数矩阵.除特别说明的元素外，其余均为0.

其中：

进一步整理得末端带负载时关节力矩表达式方程组的向量形式：

(10)

PrL1=Jm1+IZZ1+0.04m2，

PrL2=IZZ2+IZZ3+IZZ4+0.04m3rx3+0.4m4rx4，

PrL3=m2rx2+m3rx3+m4rx4，

PrL4=m2ry2-m3ry3-m4ry4，PrL5=m3+m4.

其中，IZZ4为负载相对于坐标系{4′}的Z方向上的主惯性矩，可由平行移轴公式得到；rx4、ry4为负载质心在连杆坐标系{4′}下的坐标值.表达式中出现的变量的意义与前面提到的相同.通过量纲分析，可知PrL1、PrL2的单位为N·m·s2/rad，PrL3、PrL4的单位为kg·m，PrL5的单位为kg.

AL为3×13系数矩阵.除特别说明的元素外，其余均为0.

其中：

比较不带负载与带负载情况下关节力矩的符号表达式，易知可辨识参数同为13个，且两组方程式向量形式的系数矩阵相同，即A=AL;不同之处在于当末端带负载时，

PrL2=IZZ2+IZZ3+IZZ4+0.04m3rx3+0.4m4rx4，

PrL3=m2rx2+m3rx3+m4rx4，

PrL4=m2ry2-m3ry3-m4ry4，PrL5=m3+m4，

其余可辨识参数的符号表达式与不带负载时相同.

2 基于傅里叶级数的动力学参数辨识激励轨迹设计

参数q0j、aji和bji的选择决定机器人运行的激励轨迹是否能激发出动力学参数的特性，从而影响动力学参数辨识精度.通过以下步骤确定参数q0j、aji和bji.

步骤1 确定各个关节对位置、速度、加速度的约束条件.记i=0.

步骤2 在一定范围内，随机生成3个关节对应的3条激励轨迹各自的参数q0j、aji和bji.随机数生成的范围通过经验知识和试验确定.

步骤3 将参数q0j、aji和bji代入上面的傅里叶级数表达式，计算理论位置、速度、加速度是否符合步骤1中的约束条件.若符合则继续步骤4；否则返回步骤2，并令i=i+1.

步骤4 以0.001 s为间隔，按激励轨迹分别计算机器人3个关节在一个周期(由基本角频率可以计算出激励轨迹的周期为12.5 s)内各个时刻的理论位置、速度、加速度.将每一时刻的位置、速度、加速度代入前文的系数矩阵A可计算出对应该时刻的系数矩阵Ak(k=1,2,3,…,12 500).

步骤5 将所有矩阵Ak合并成一个总矩阵HA

借助Matlab计算矩阵HA的二范数条件数Condi，并记录该条件数与对应的参数q0j、aji和bji.

步骤6 令i=i+1，并返回步骤2，直至i=100.

找出计算得到的二范数条件数中最小的一个，并将对应的激励轨迹作为实验用机器人激励轨迹.

3 实验及数据处理

3.1 实验装置及实验步骤

图5为国内某公司生产的SCARA机器人，可运动轴数为4，额定负载2 kg，最大负载5 kg.第1轴和第2轴最高角速度可达600°/s，在笛卡尔坐标下第1轴和第2轴合成运动最高速度可达6.3 m/s；第3轴最高速度可达1.3 m/s；第4轴最高角速度可达1 667°/s.在笛卡尔坐标下，第1轴和第2轴合成运动时，机器人末端在水平面的重复定位精度可达±0.01 mm；第3轴运动时，机器人末端在铅锤面的重复定位精度可达±0.01 mm.在关节坐标下，第4轴旋转时机器人末端的重复定位精度可达±0.005°.该型号机器人原本配备驱控一体控制器，经协商后改为EtherCAT总线控制，采用intimes实时控制系统，控制周期可达1 ms，能采回电机编码器信号以及电机电流信号.

图5 SCARA机器人Fig.5 SCARA robot

实验步骤如下：

步骤1 SCARA机器人在不带负载条件下运行一次激励轨迹，并且在每个控制周期读取当前时刻的电机编码器值和电机电流值.

步骤2 SCARA机器人在带负载条件下运行一次激励轨迹，并且在每个控制周期读取当前时刻的电机编码器值和电机电流值.

步骤3 处理实验数据，用最小二乘法计算可辨识动力学参数集，得到关节力矩公式.

步骤4 在带负载条件下运行另一条轨迹，获取实际力矩值，并与关节力矩公式计算得到的理论值进行比较，验证动力学参数辨识方法的正确性.

3.2 数据处理

根据关节电机型号查阅说明资料，将读取到的电机编码器值及电机电流值转换为关节位置值以及关节力矩值.通过中心差分的方法由关节位置值获得关节速度和关节加速度.利用三阶低通高斯滤波方法对关节位置、速度、加速度以及关节力矩值进行滤波，将获得的滤波值用于动力学参数辨识.在此动力学参数辨识中采用最小二乘法：

X=(A′TA′)-1A′TY

(11)

表2为分别在带负载与不带负载情况下采用最小二乘法辨识得到的可辨识动力学参数集，各个参数的具体符号表达式与前文相同.

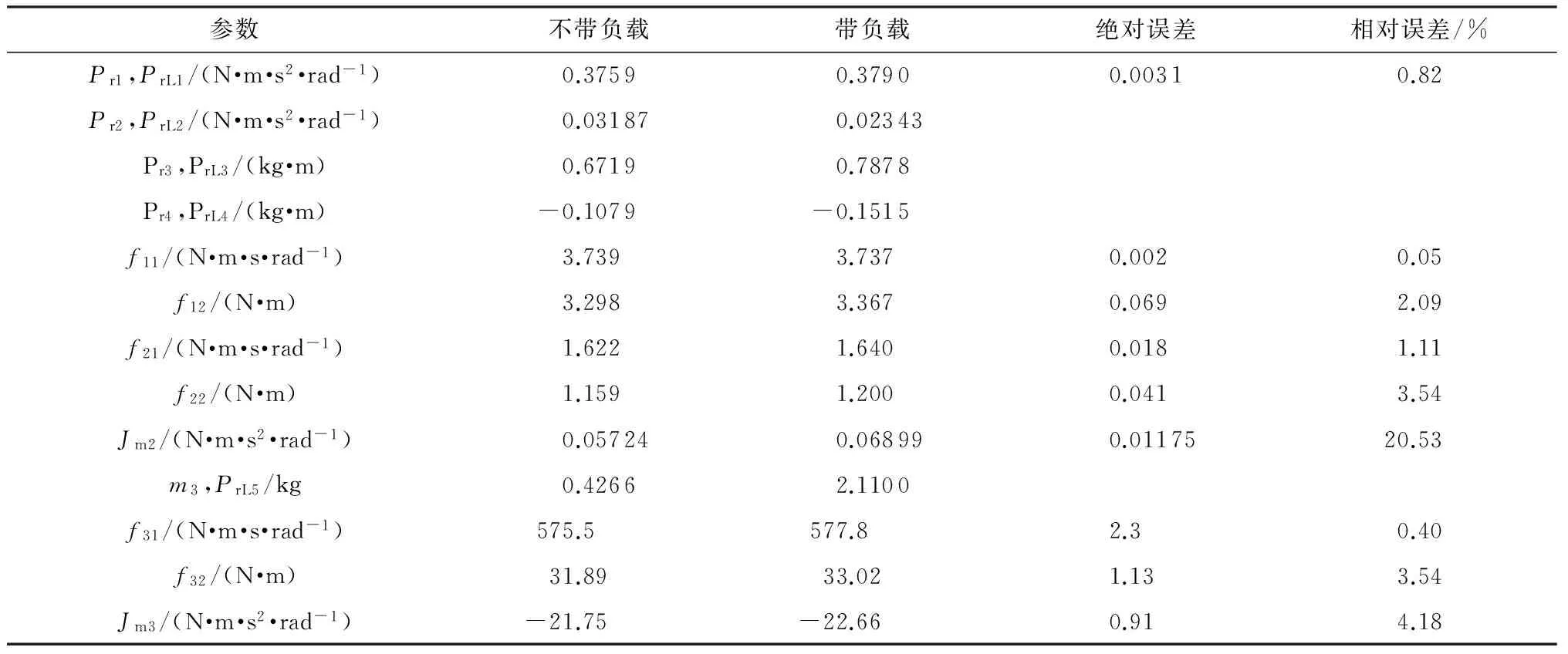
表2 动力学参数辨识结果Table 2 Result of dynamic parameter identification

从前文对可辨识参数集符号表达式的分析比较可知，带负载的可辨识参数与不带负载的可辨识参数相比，Pr1、f11、f12、f21、f22、Jm2、f31、f32、Jm3理论上不发生变化.而实际上这9个参数都发生了变化.但除Jm2的相对误差为20.53%，其余均在5%以内，而且Jm2的绝对误差并不大.经分析，误差出现的原因可能有两个方面:一是数据处理方法，由于速度与加速度是通过中心差分的方法获得，虽然经过了滤波，但是不能保证噪声已被完全过滤；二是参数辨识方法，最小二乘法获得的是使关节力矩的采样电流估计值与理论计算值的误差平方和最小的一组参数值，而且不带负载与带负载条件下获得的是两组不同的数据，即使理论上两次计算中某些参数应当相等，由最小二乘法计算得到的结果可能并不一样.

PrL2、PrL3、PrL4、PrL5这4个参数会因为附加载荷而改变.由前文得负载的变化对可辨识参数集的影响为

DFF2=PrL2-Pr2=IZZ4+0.4m4ry4，

DFF3=PrL3-Pr3=m4rx4，

DFF4=PrL4-Pr4=-m4ry4，

DFF10=PrL5-m3=m4.

由DFF10可得载荷质量，代入上表数据算得m4=1.683 7 kg；实际用电子秤测得载荷质量为1.882 9 kg，辨识结果误差较小.误差来源仍可能是前文所提两方面，即数据处理方法和最小二乘辨识方法.同理，DFF2、DFF3、DFF4的理论计算结果与上表中两次辨识得到的结果的差值也不一定能完全相等.但可看出DFF2、DFF3、DFF4、DFF10实际值的变化趋势与对应的符号表达式是一致的.

在带负载条件下让机器人运行区别于激励轨迹的另一条轨迹，通过比较实际采样电流换算的关节力矩值与公式计算的理论值是否一致，验证基于文中辨识方法所得动力学参数估计关节力矩方法的可行性.

图6(a)、图7(a)、图8(a)为各个关节实际测得的电机电流值换算得到的关节力矩，以下称原始力矩值.图6(b)、图7(b)、图8(b)中，虚线为原始关节力矩值经三阶低通高斯滤波后获得的滤波值，实线为由前文的关节力矩公式代入本节辨识所得动力学参数后计算出的力矩值，公式中用到的关节速度、加速度采用中心差分后经三阶低通高斯滤波获得.

从图6-8中可看出，由关节力矩公式计算出的力矩值与原始力矩值变化趋势相同.说明文中建立的动力学模型精度较好，所提动力学参数辨识方法是可行的.借助Matlab进一步分析各关节力矩的理论计算值和滤波值,由于实验中没有安装关节力矩传感器，文中以电机采样电流换算的关节力矩值的三阶低通高斯滤波值作为理论真值.关节1力矩理论计算值与理论真值的最大绝对误差为0.56 N·m，均方根误差为0.656 8;关节2力矩理论计算值与理论真值的最大绝对误差为0.84 N·m，均方根误差为0.368 7;关节3力矩理论计算值与理论真值的最大绝对误差为23.16 N·m，均方根误差为11.18.虽然对第3轴移动关节的关节力矩的估计不如前两轴旋转关节的精确，但是SCARA机器人的定位主要依赖于前两个旋转关节，而对前两轴旋转关节的力矩估计是比较精确的，这样的结果对应用而言可以接受.此外，通过添加关节力矩实时滤波算法，可使关节力矩估计值更精确.但滤波算法不是文中重点，在此不再赘述.

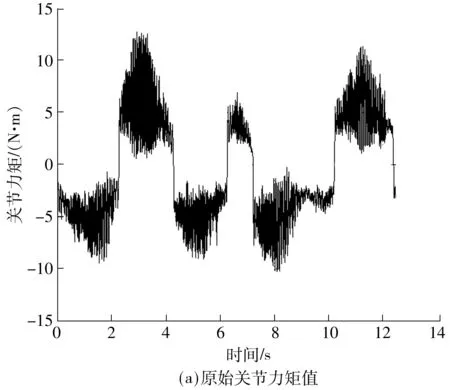
图6 第1轴关节力矩图Fig.6 Torque of joint 1

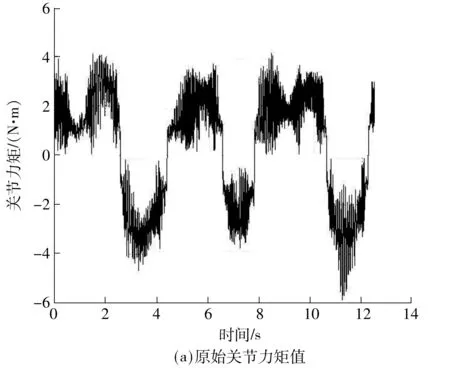
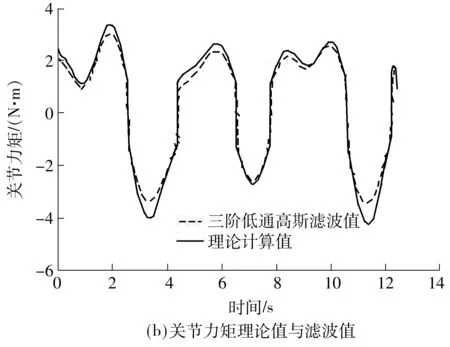
图7 第2轴关节力矩图Fig.7 Torque of joint 2

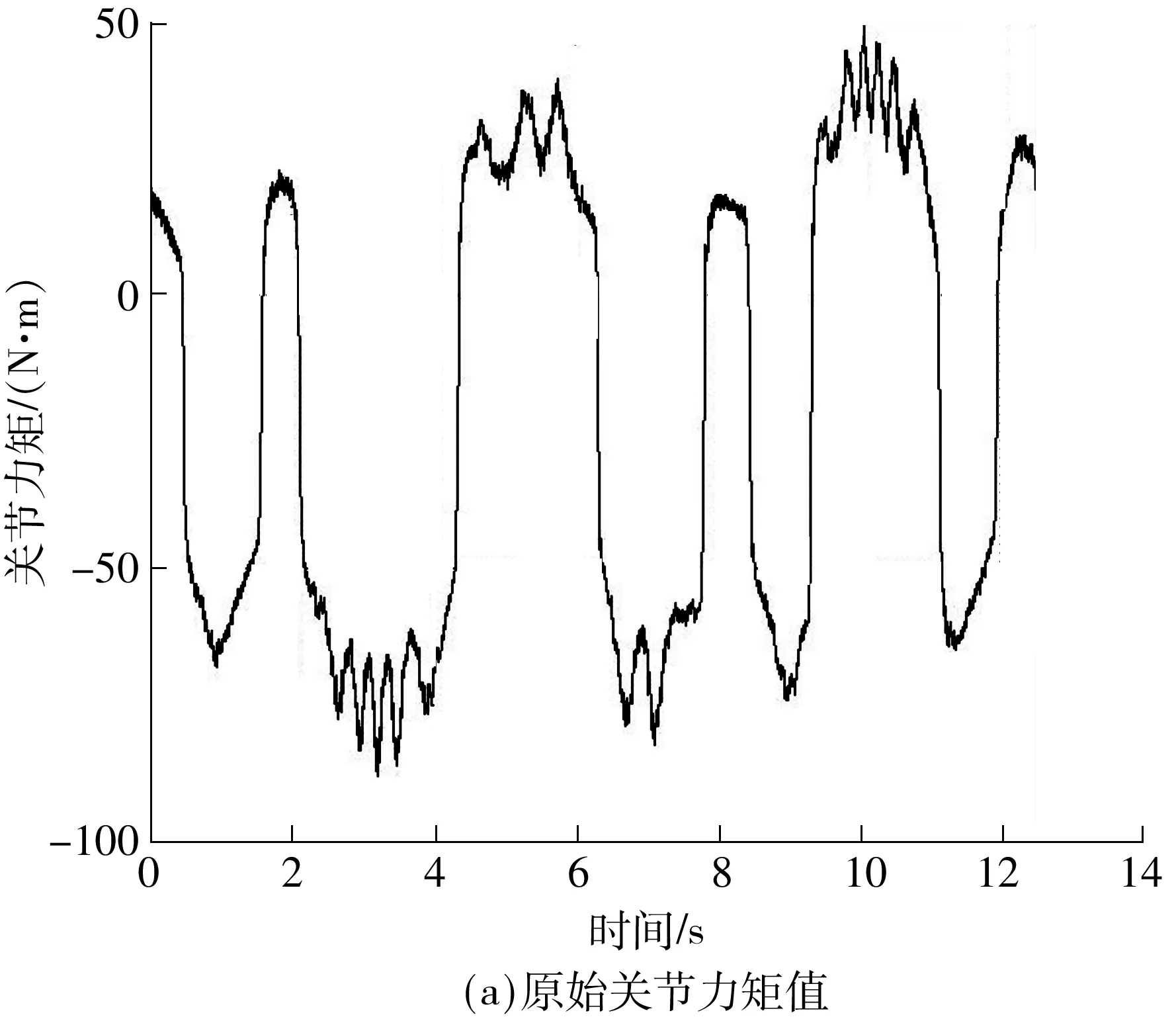
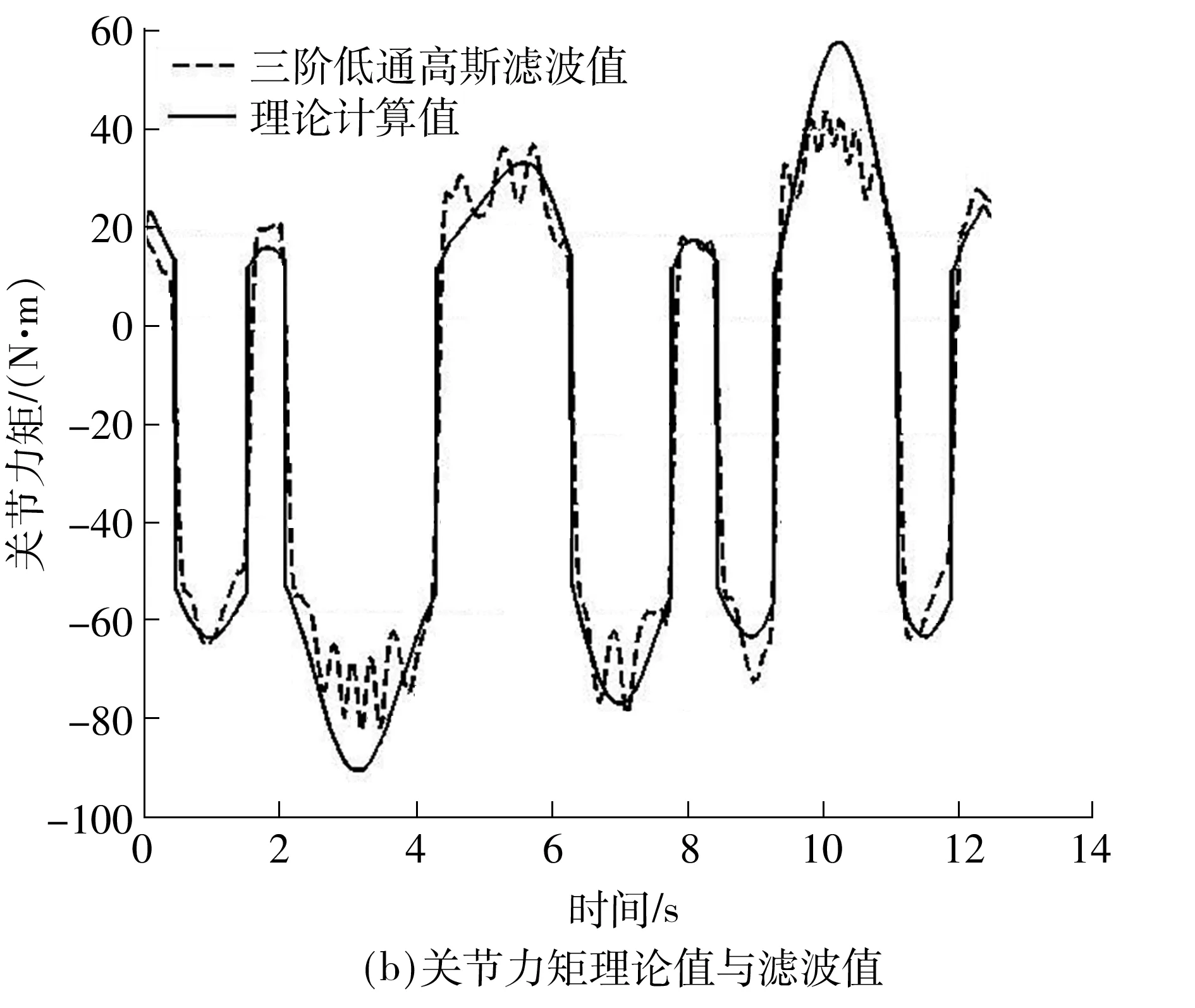
图8 第3轴关节力矩图Fig.8 Torque of joint 3

4 结论

动力学参数辨识是机器人动力学控制的基础.动力学参数精度直接影响动力学模型精度.机器人动力学模型精度越高，对运动时机器人关节力矩的估计就越精确，后续对机器人的力控制效果就越好.文中利用牛顿欧拉法对SCARA机器人进行动力学建模，同时考虑摩擦力和电机转子对关节力矩的影响，整理出了机器人关节力矩关于一组动力学可辨识参数集的线性表达式.在此基础上，结合傅里叶级数激励轨迹实验和最小二乘方法对SCARA机器人动力学可辨识参数集进行了辨识.从实验数据可以看出，使用文中的辨识方法得到的动力学参数集构造出的动力学方程能较好地估计出SCARA机器人运行时的关节力矩.后续研究中，提高参数辨识精度可从以下方面入手：一是建模时进一步分析传动机构，找出可能被忽视的动力学关系，并对其建模；二是从数据处理方式入手，提高速度、加速度求取精度及辨识方法精度.同时，考虑到参数辨识的最终目的是基于动力学建模的机器人力控制，后续工作中将结合读取到的关节力矩信号设计关节力矩实时滤波算法.

[1] WANG N,LIU J,WEI S,et al.The control system design of a SCARA robot [C]∥Proceedings of International Conference on Intelligent Robotics and Applications.Guangzhou:Springer International Publishing,2014:136- 145.

[2] 刘欢欢.基于TwinCAT平台的SCARA机器人运动控制算法研究 [D].哈尔滨：哈尔滨工业大学,2015.

[3] 刘正士,陈恩伟,干方建.机器人惯性参数辨识的若干方法及进展 [J].合肥工业大学学报(自然科学版),2005,28(9):998- 1003.

LIU Zheng-shi,CHEN En-wei,GAN Fang-jian.Review of some methods for identifying inertial parameters of robots and their development [J].Journal of Hefei University of Technology(Natural Science),2005,28(9):998- 1003.

[4] ARMSTRONG B,KHATIB O,BURDICK J.The explicit dynamic model and inertial parameters of the PUMA 560 arm [C]∥Proceedings of 1986 IEEE International Conference on Robotics and Automation.San Francisco:IEEE,1986:510- 518.

[5] 王树新,张海根,黄铁球,等.机器人动力学参数辨识方法的研究 [J].机械工程学报,1999,35(1):23- 26.

WANG Shu-xin,ZHANG Hai-gen,HUANG Tie-qiu,et al.Study on dynamic parameter identification of robot [J].Journal of Mechanical Engineering,1999,35(1):23- 26.

[6] CHAN S P.An efficient algorithm for identification of robot parameters including drive characteristics [J].Journal of Intelligent and Robotic Systems,2001,32(3):291- 305.

[7] URREA C,PASCAL J.Design,simulation,comparison and evaluation of parameter identification methods for an industrial robot [J].Computers & Electrical Engineering,2016:1- 16.

[8] JIANG Z H,SENDA H.Dynamic parameter identification of robot arms with servo-controlled electrical motors [C]∥Proceedings of SPIE-The International Society for Optical Engineering.Chongqing:SPIE,2005:604235.

[9] 丁亚东,陈柏,吴洪涛,等.一种工业机器人动力学参数的辨识方法 [J].华南理工大学学报(自然科学版),2015,43(3):49- 56.

DING Ya-dong,CHEN Bai,WU Hong-tao,et al.An identification method of industrial robot’s dynamic parameters [J].Journal of South China University of Technology (Natural Science Edition),2015,43(3):49- 56.

[10] 丁力,吴洪涛,姚裕,等.基于WLS-ABC算法的工业机器人参数辨识 [J].华南理工大学学报(自然科学版),2016,44(5):90- 95.

DING Li,WU Hong-tao,YAO Yu,et al.Parameters identification of industrial robots based on WLS-ABC algorithm [J].Journal of South China University of Technology (Natural Science Edition),2016,44(5):90- 95.

[11] CRAIG J J.Introduction to robotics:mechanics and control [M].3rded.Upper Saddle River:Pearson Prentice Hall,2005.

[12] ZOLLO L,LOPEZ E,SPEDALIERE L,et al.Identification of dynamic parameters for robots with elastic joints [J].Advances in Mechanical Engineering,2015,7(2):843186.

[13] ZHU S,CHEN Q,WANG X,et al.Dynamic modelling using screw theory and nonlinear sliding mode control of serial robot [J].International Journal of Robotics and Automation,2016,31(1):63- 75.

[14] 丁亚东.工业机器人动力学参数辨识 [D].南京：南京航空航天大学,2015.

[15] SOUSA C J S D.Dynamic model identification of robot manipulators:solving the physical feasibility problem [D].Coimbra:University of Coimbra,2014.