基于Runge-Kutta的NURBS曲线实时前瞻插补算法*
2017-03-08吴玉香王鹏
吴玉香 王鹏
(华南理工大学 自动化科学与工程学院, 广东 广州 510640)
传统数控系统只能实现直线插补、圆弧插补以及螺旋插补.大多数场合下,这些插补方法能满足基本加工需求.但是,一些复杂曲面物体在CAD/CAM系统中都是采用参数曲线、曲面来表达的,例如NURBS曲线能精确地表达各种复杂的曲面造型,因此NURBS曲线插补广泛应用于各种高端数控设备中.然而在加工领域,传统方法是将NURBS曲线划分为大量微小直线段或圆弧段,然后进行直线插补或圆弧插补[1],这将导致加工速度受到更多约束,产生剧烈波动,严重影响了加工效率和精度.
近年来,国内外学者对NURBS曲线直接插补算法进行了大量研究.文献[2]提出了恒定参数插补算法,即以恒定的参数增量计算下一个插补参数,但此方法在曲率较大位置处误差过大,若要降低误差则要降低增量,插补效率将会降低.文献[3]提出了基于一阶泰勒展开法的NURBS曲线插补算法,但存在进给速度波动过大的问题.文献[4]提出了基于二阶泰勒展开式的直接插补算法,该算法引入了二阶求导,计算量大大增加,影响实时性.由于泰勒展开法不能兼顾精度和运算复杂度,一些学者开始采用迭代逼近法来实现高精度插补.文献[5]提出了一种基于牛顿迭代法的直接插补算法;文献[6]提出了基于二分法的高精度插补算法,大大降低了进给速度的波动率,但是迭代次数过多,降低了插补实时性;文献[7]提出了一个通用的参数曲线迭代插补方法,相比牛顿迭代法和二分法该方法计算量较小,并且精度较高;文献[8]提出了一种进给速度根据弓高误差进行自适应调整的插补算法,但是该算法没有考虑机床的加减速性能;文献[9]提出了基于预处理的进给速度规划方法,在曲率较大的地方采用基于逐点比较计算的方法规划每个参数点处的速度,但该方法在实时插补过程中计算量较大,实时性不高;文献[10]采用了基于5段S曲线加减速控制方法进行速度规划,改善了进给速度的平滑性,但是对曲率频繁变化的曲线控制效果不佳.
文中在以上研究的基础上,采用四阶经典Runge-Kutta方法计算插补参数,通过对弓高误差和法向加速度的约束控制来实现进给速度自动调整.为了降低加工过程中进给速度的波动率,设计了插补参数校正公式,能快速将速度波动率调整至加工要求精度范围内.同时提出一种新的前瞻控制方法,根据预处理得到的进给速度极值点对NURBS曲线进行分段处理,依次对每一个前瞻插补区间段进行速度前瞻控制,从而避免加速度超出机床加减速能力,减小机床受到的冲击.最后在Matlab仿真平台上进行了仿真实验,对算法的有效性进行验证.
1 基于Runge-Kutta的进给速度自动调整插补算法
1.1 NURBS曲线定义
k次NURBS曲线的数学表达式如下[11- 12]:
(1)
其中:u为NURBS方程的参数;k为正整数;di为控制点,组成一个控制多边形,ωi为对应控制点的权因子;Ni,k(u)为定义在非周期节点矢量U上的k次B样条基函数,节点矢量为
(2)
通常取u0=…=uk=0,un+1=…=un+k+1=1,其余取值介于0~1且单调递增.k次基函数Ni,k(u)递推式为
(3)
其中规定0/0=0.
1.2 插补参数计算
传统NURBS曲线直接插补采用泰勒展开法计算插补参数值,阶数低时精度不够,阶数高时计算量大.为达到较高的加工精度并避免高阶求导,文中采用了经典Runge-Kutta方法求解插补参数值,计算公式如下[13]:
(4)
式中,xi为当前时刻,yi为当前时刻对应值,h为时间间隔,K1为开始时刻的斜率,K2为根据K1计算的时间段中点的斜率,K3为根据K2计算的时间段中点的斜率,K4为结束时刻的斜率.
数控系统的插补过程为:在ti时刻的插补点参数值ui,给定进给速度V(ui),需要计算出下一插补点的参数ui+1,对应时刻为ti+1,T为插补周期,T=ti+1-ti,建立以下一阶非线性微分方程求解模型:
(5)
在三维空间中,根据瞬时速度定义可知,在插补点C(ui)处进给速度V(ui)为
(6)
得
(7)
令x=Cx(u),y=Cy(u),z=Cz(u),则有
(8)
已知当前插补点参数为ui,给定进给速度为V(ui),则计算插补参数u的迭代公式为
(9)
其中,K1=f(ui),K2=f(ui+K1T/2),K3=f(ui+K2T/2),K4=f(ui+K3T).
根据式(9)所得的ui+1,通过NURBS曲线的定义式(1)可以计算出下一个插补点C(ui+1)的三维坐标,进而得到当前插补周期实际进给步长:
ΔLi=‖C(ui+1)-C(ui)‖
(10)
1.3 进给速度的自动调整
插补过程中,刀具在插补周期内做直线运动,即用弦长逼近弧长,会存在弓高误差,如图1所示.若机床以给定的指令速度Vm恒速插补,则在曲线曲率较大的地方弓高误差较大.当加工精度要求较高时相应的进给速度需要降低.此外,根据机床的动力学特性,在曲率较大的地方,进给速度会受到法向加速度的限制.为提高加工质量,进给速度规划同时需考虑弓高误差约束和法向加速度约束.
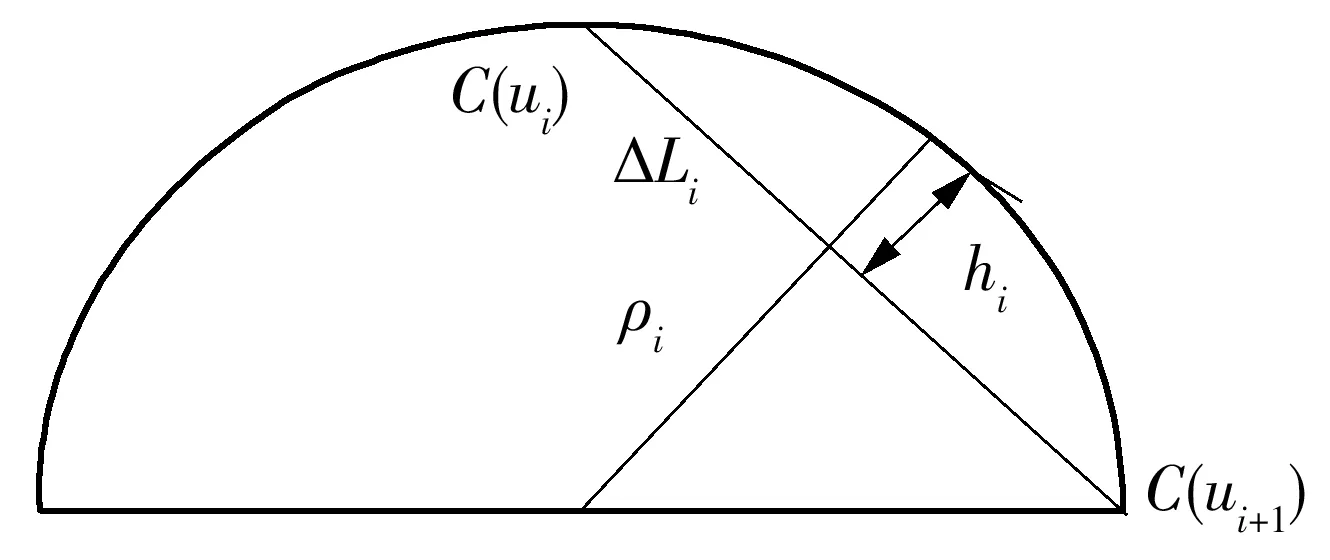
图1 弓高误差示意图Fig.1 Schematic diagram of chord error
1.3.1 弓高误差约束的进给速度
插补过程中通常进给步长很小,在一个插补周期内,将弦长ΔLi对应的NUBRS微小曲线段近似为圆弧处理,圆弧半径为插补点C(ui)处的曲率半径ρi,如图1所示.
根据几何关系,弓高误差为
(11)
曲率半径ρi的计算公式为[14]
(12)
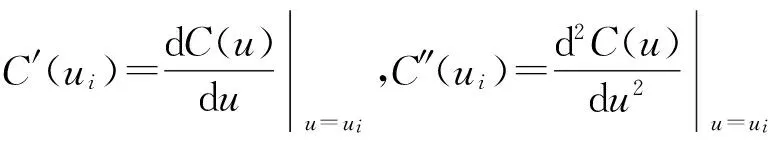
加工过程中,允许的最大弓高误差为hmax,插补点曲率越大,曲率半径越小,因此在满足加工精度的条件下允许的进给速度越小,基于弓高误差约束条件的最大进给速度为[15]
(13)
1.3.2 法向加速度约束的进给速度
刀具在高速移动过程中,为了保证加工精度,还需考虑机床的惯性,因此刀具在运动过程中有一个法向加速度的限制.如图2所示,刀具的进给速度V(ui)、法向加速度ai以及当前插补点C(ui)的曲线半径ρi之间的数学关系为[16]
(14)
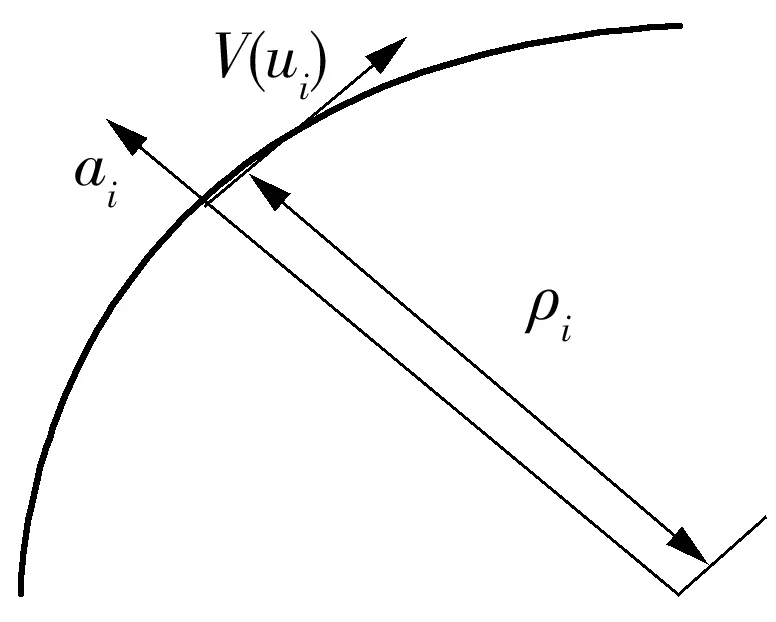
图2 进给速度与法向加速度分布Fig.2 Distribution of federate and normal acceleration
加工过程中,任意插补点的法向加速度必须满足ai≤an,max,能达到的最大进给速度为
(15)
其中,an,max为机床允许的最大法向加速度.
1.3.3 进给速度自动调整规则
刀具在插补过程中,随着曲线曲率的改变,为了保证加工精度,进给速度需要作出相应的调整.根据式(13)和(15),当加工过程中最大弓高误差hmax和最大法向加速度an,max确定之后,文中设计的进给速度调整规律如下:
V(ui)=min{Vm,Ve(ui),Vn(ui)}
(16)
对应的预估进给步长ΔLp,i为
ΔLp,i=V(ui)T
(17)
其中,Vm为机床给定最大进给速度.
1.4 插补参数校正
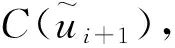
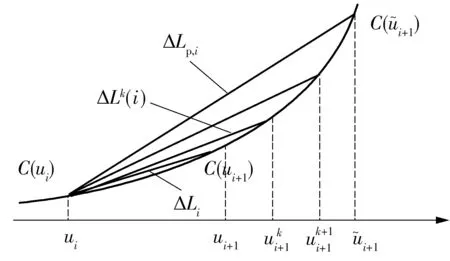
图3 进给速度波动产生的原理图Fig.3 Schematic diagram of the origin of federate fluctuation
实际进给速度为Vre(ui):
(18)
进给速度的波动大小用速度波动率δi衡量.
(19)
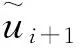
(20)
(21)
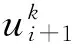
2 NURBS曲线前瞻控制算法
曲线曲率变化剧烈的地方,加速度可能超出机床允许的最大值,机床无法按照上述进给速度进行插补,需要对曲率变化剧烈区域的进给速度进行前瞻控制,才能满足加工精度要求[17].
2.1 对NURBS曲线进行前瞻分段
根据1.3节中的策略得到的进给速度曲线,通常在曲率极值点的给定进给速度为一个速度极值点.若V(ui)满足:
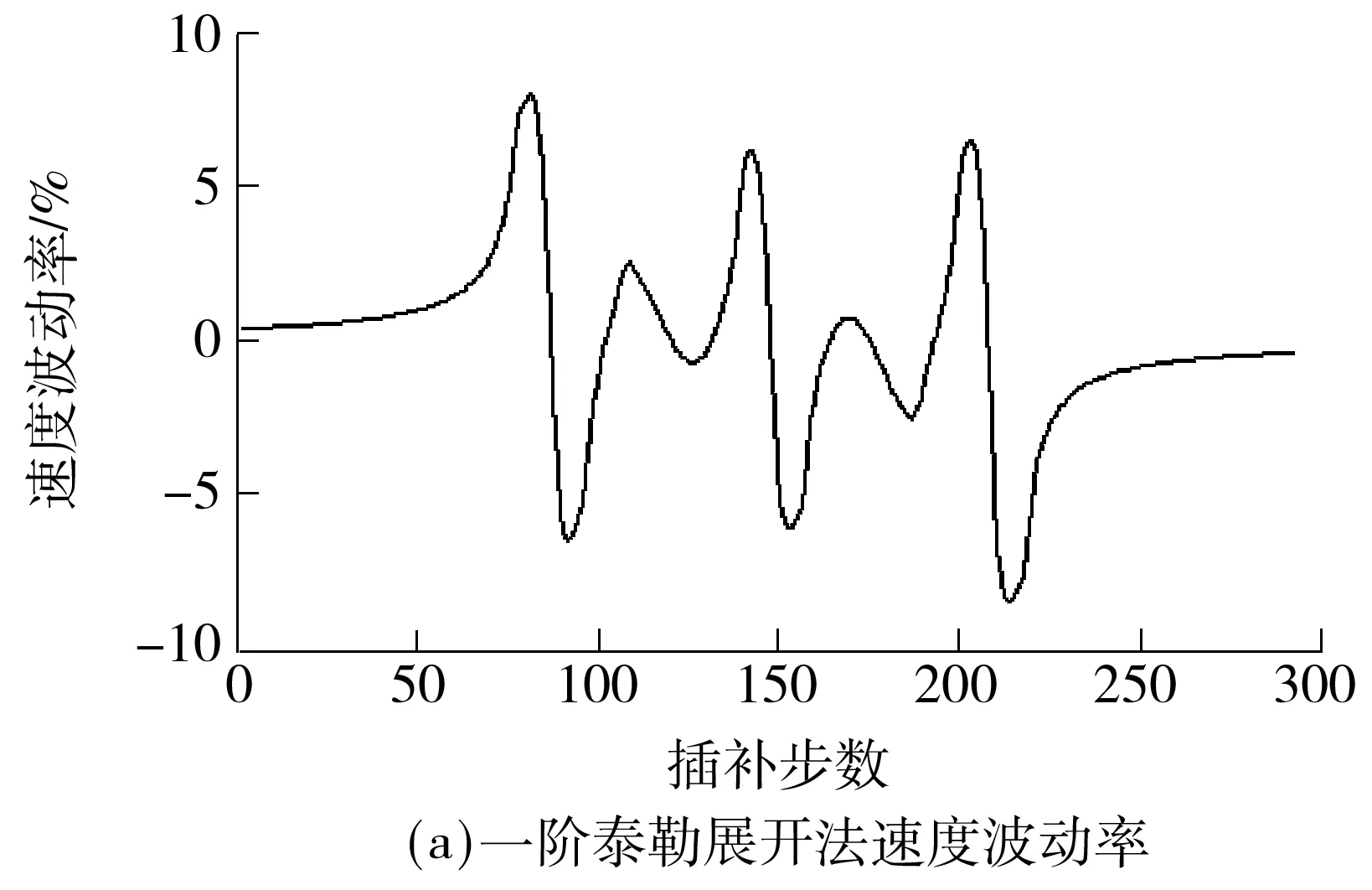
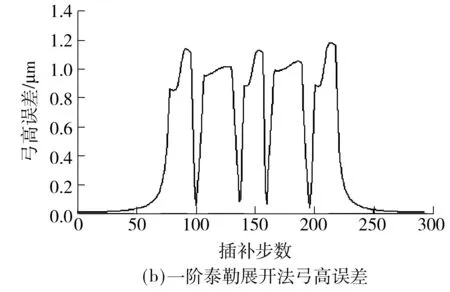
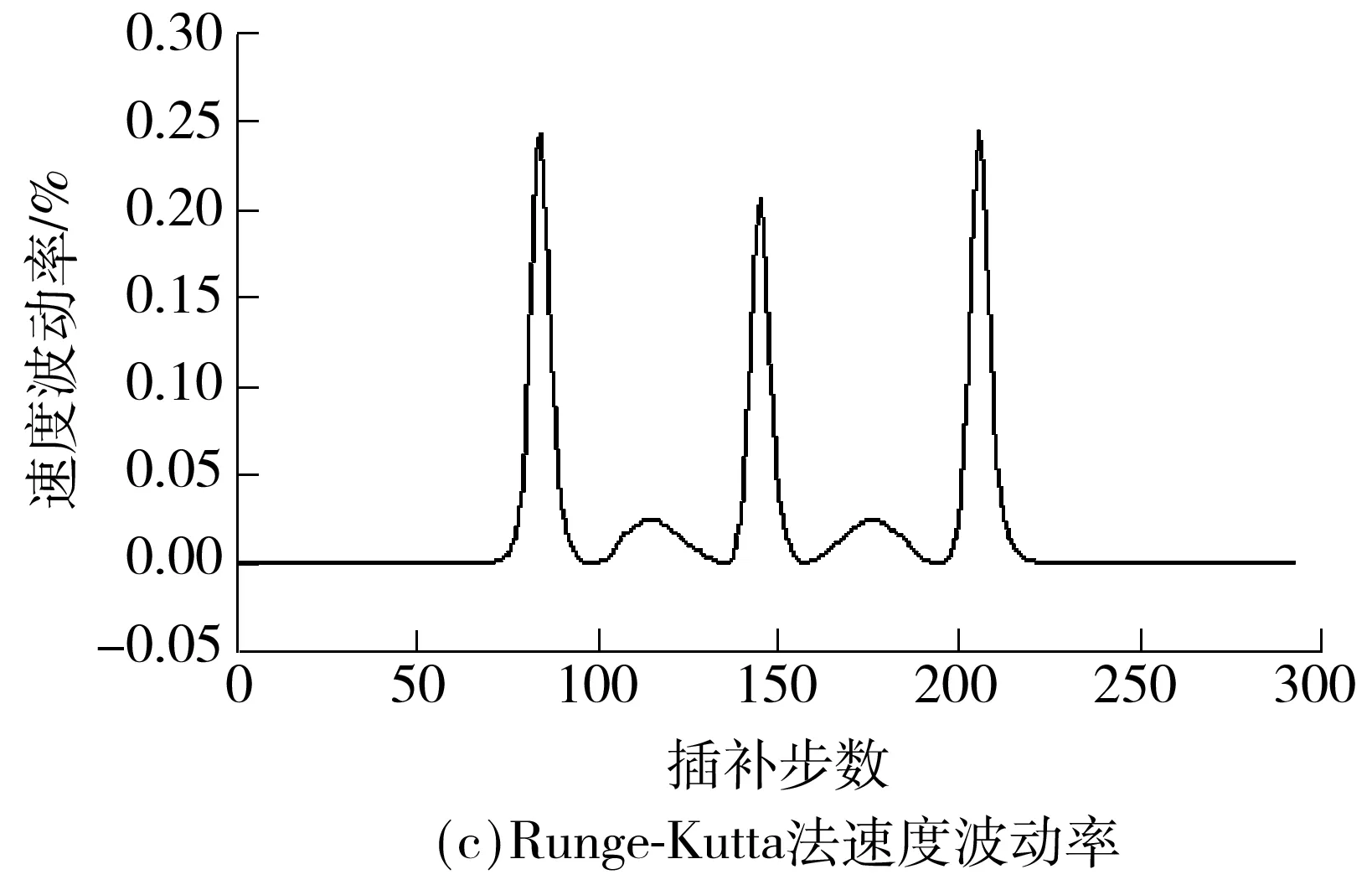
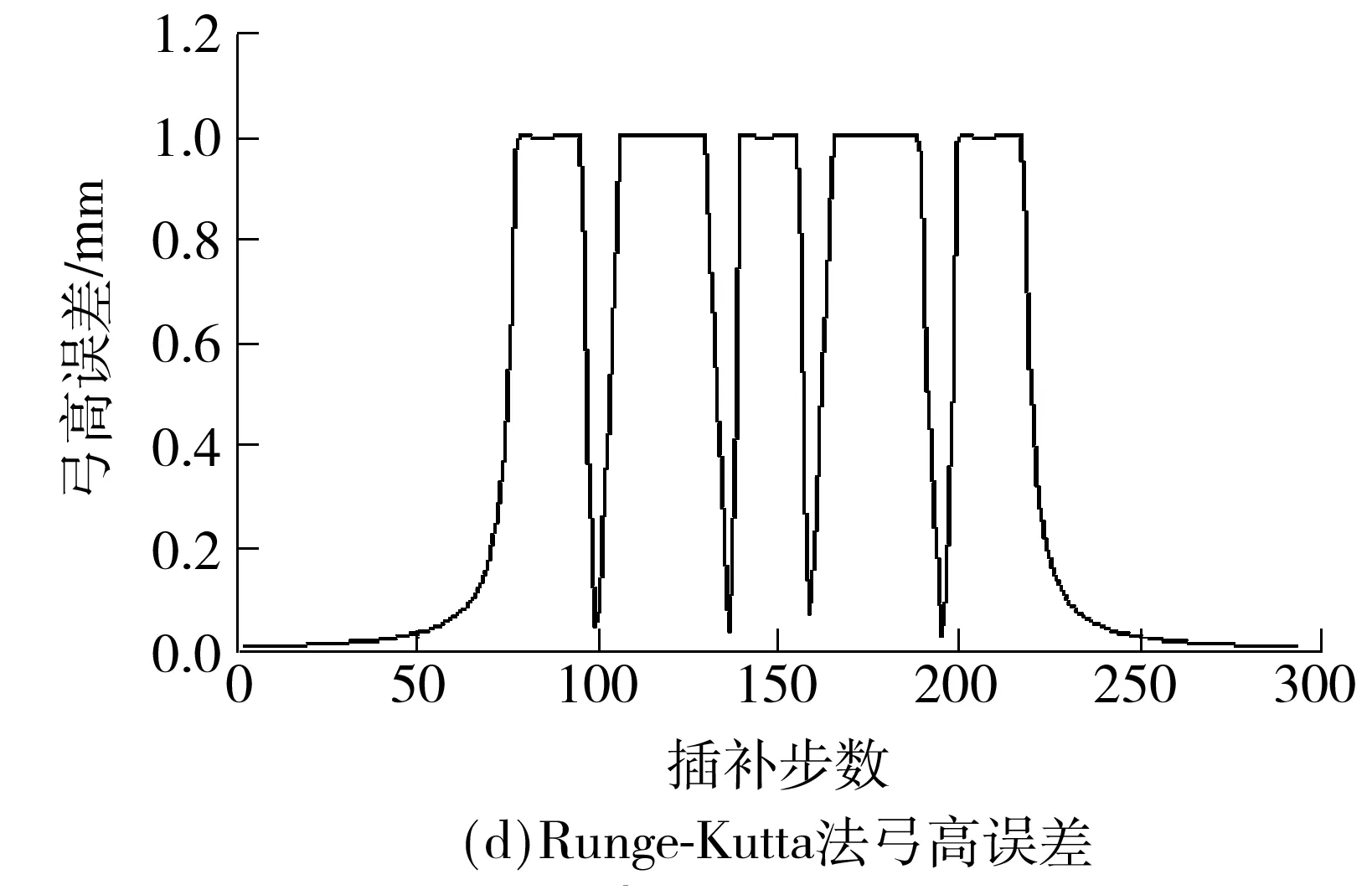
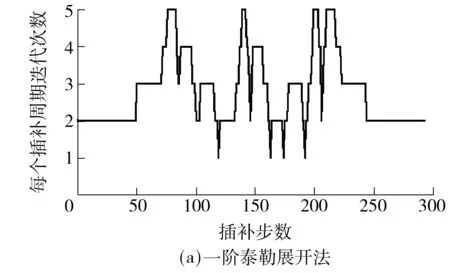
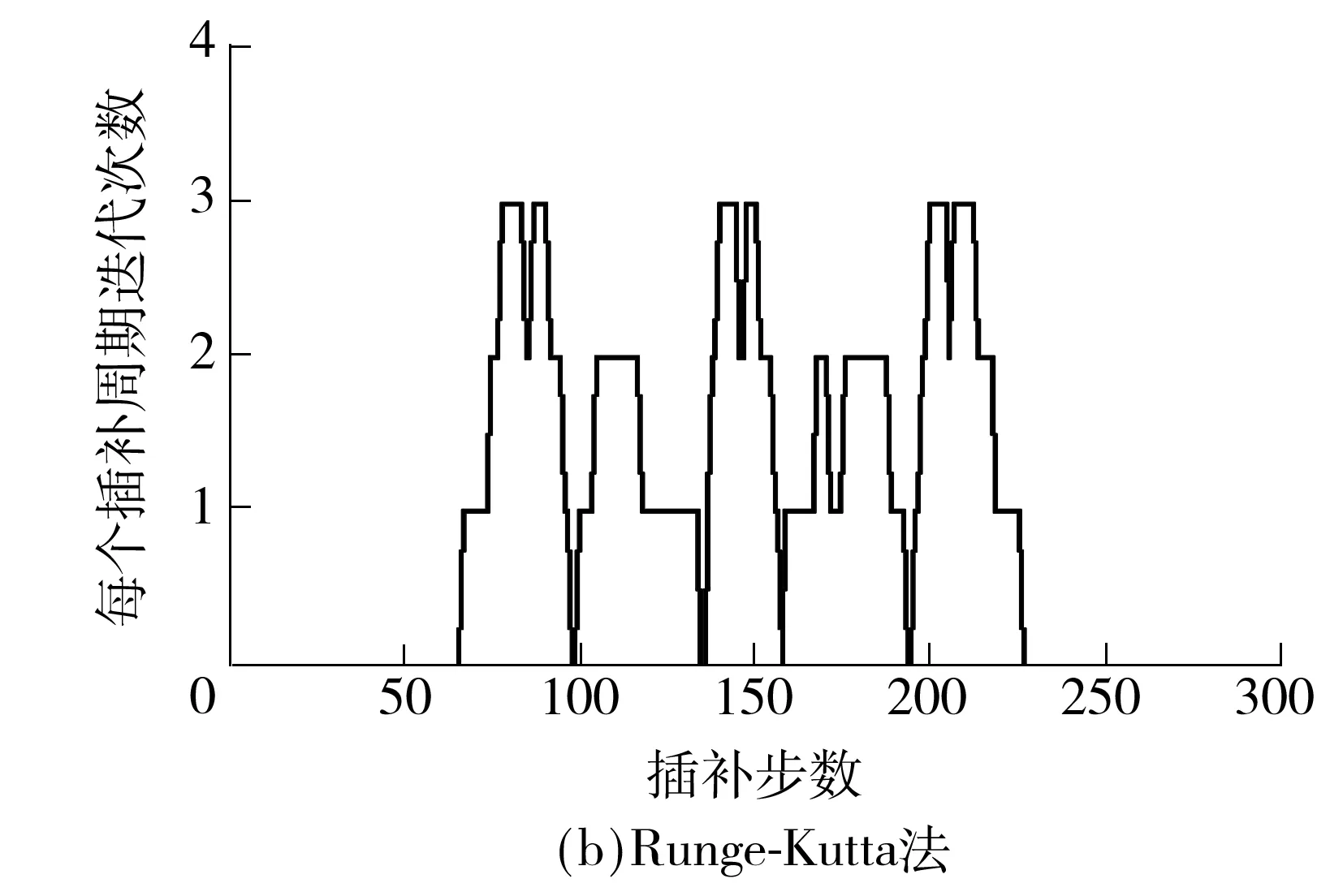
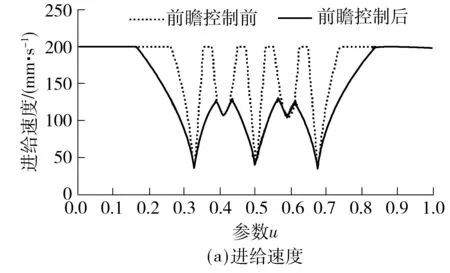
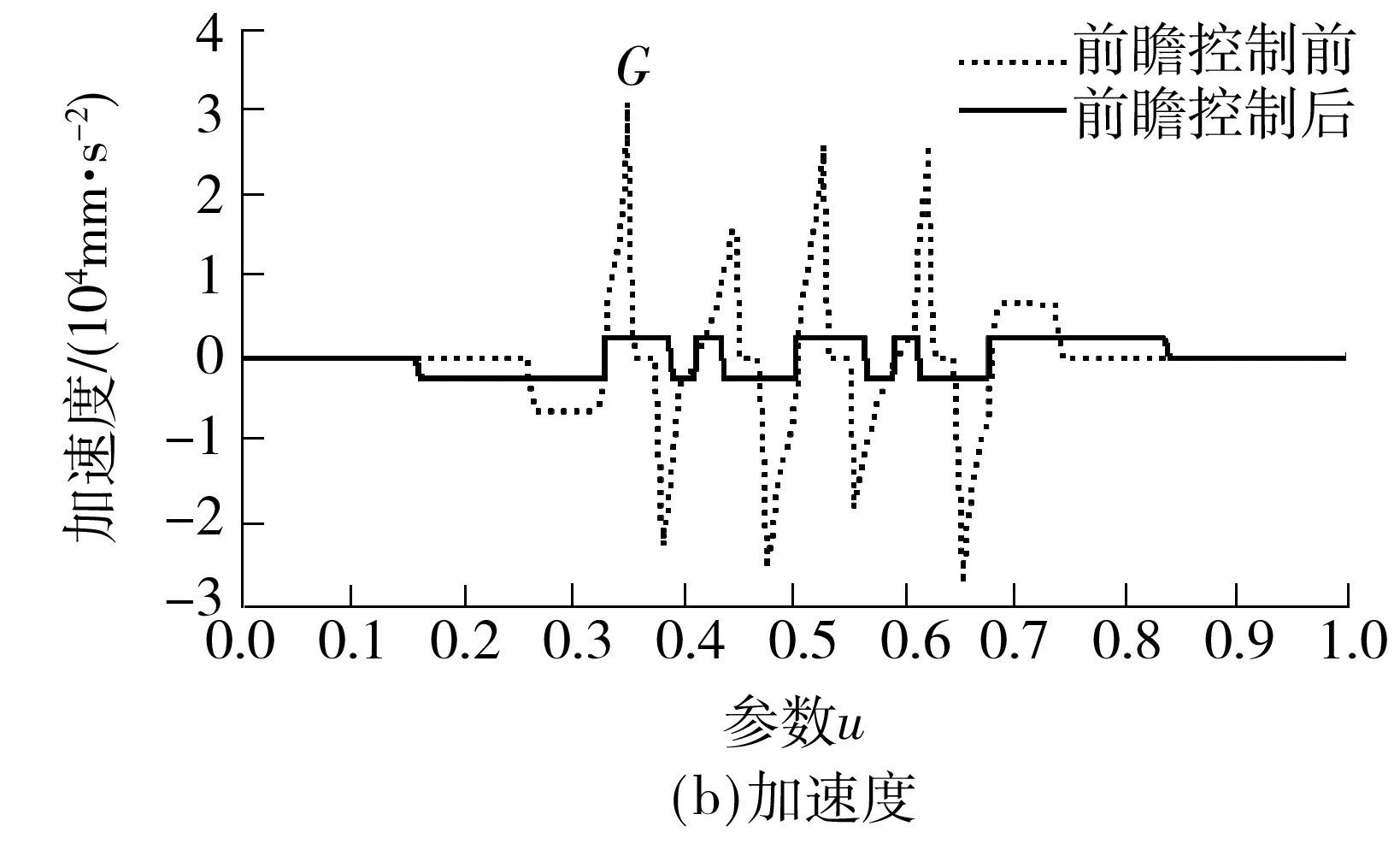
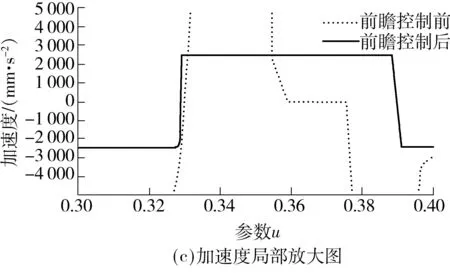
V(ui) (22) 且 V(ui) (23) 则V(ui)为一个速度极值点,记为Vs(j),j=1,2,…. 如图4所示,容易判定图中进给速度Vs(1)、Vs(2)、Vs(3)、Vs(4)、Vs(5)分别为速度极值点,将加工曲线起点、终点及以上各速度极值点任意相邻两点之间的曲线段划分为一个前瞻插补区间. 图4 粗插补过程中的速度极值点示意图 Fig.4 Schematic diagram of the federate extreme point in rough interpolation 利用粗插补得到的离线数据,分别识别并保存速度极值点的进给速度Vs(j)、速度极值点距起点的插补距离Ss(j). C(ui+1)到曲线起点的距离S(ui+1)的计算公式为 S(ui+1)=S(ui)+V(ui)T (24) 其中:i=0,1,2,…;S(u0)=0;V(ui)为插补点C(ui)处进给速度. 插补点加速度超出机床允许的最大值称为速度敏感点,其判别公式为 (25) 式中,A为机床最大加速度,则V(ui)为速度敏感点. 找到速度极值点Vs(j)左右两侧最近速度敏感点Vsl(j)和Vsr(j),距加工起点距离分别为Ssl(j)、Ssr(j).在任意前瞻插补区间,速度敏感点Vsr(j)与Vsl(j+1)之间的区间进给速度需要重新规划.在满足机床最大加速度的要求下,进给速度从Vsr(j)加(减)到Vsl(j+1)需要的最短加(减)速距离为 (26) 这两点之间的插补距离为 Ls(j)=Ssl(j+1)-Ssr(j) (27) 首先考虑加速情况,即Vsr(j) 图5 速度重新规划示意图Fig.5 Schematic diagram of the re-planning federate 对于图5(a),此时由于Ls(j) (28) 而当Ls(j)>Lmin(j)时,表明进给速度能以最大加速度从Vsr(j)增加到Vsr(j+1). 对于图5(b),若Ls(j)-Lmin(j)<(Vm2-Vsl2(j+1))/A,刀具能达到的最大进给速度为Vsm(j),则计算如下: (29) 对于图5(c),若Ls(j)-Lmin(j)≥(Vm2-Vsl2(j+1))/A,刀具能达到机床给定的进给速度Vm,当插补点C(ui)距加工起点的距离为S(ui)时,刀具开始减速. S(ui)=Ssl(j+1)-(Vm2-Vsl2(j+1))/(2A) (30) 减速情况与加速情况类似处理即可. 粗插补过程中,计算并保存进给速度二次规划过程中需要的数据,精插补过程中则可以直接调用相关数据,提高加工的实时性.具体步骤如下: (1)寻找速度极值点Vs(j)及其距加工起点的距离Ss(j),对NURBS曲线进行前瞻分段. (2)在每一个速度极值点附近分别找到左右两侧的首个速度敏感点Vsl(j)、Vsr(j),距加工起点的距离分别Ssl(j)、Ssr(j),第j个前瞻插补区间首末速度敏感点之间的距离如式(27),首个速度敏感点Vsr(j)加(减)速到末速度敏感点Vsl(j+1)需要的最小加(减)速距离如式(26),保存以上数据. (3)分析当前前瞻插补区间Ls(j)与Lmin(j)之间的关系,若Ls(j) (4)重复上述步骤,进行下一段插补,直到所有前瞻插补段插补完成为止. 为了验证文中所提算法的性能,分别采用基于一阶泰勒展开法和文中所提基于Runge-Kutta的NURBS曲线插补算法,在Matlab平台上进行了实例仿真.实例给定的初始条件:最大进给速度Vm=200 mm/s,插补周期T=1 ms,最大法向加速度an,max=4 900 mm/s2,最大切向加速度Amax=2 450 mm/s2,最大弓高误差hmax=0.001 mm.为突出文中所提算法的优良性能,选择一个曲率多变的3次NURBS曲线,其控制顶点(单位:mm)为(10,0)、(20,20)、(12,8)、(10,20)、(8,8)、(0,20)、(10,0);节点矢量为[0 0 0 0 0.25 0.5 0.75 1 1 1 1];权值为[1 1 1 1 1 1 1];次数为3.其控制的NURBS曲线如图6所示. 图6 给定参数的NURBS曲线Fig.6 NURBS curves with given parameters 为了证明文中算法在参数计算过程中精度高的特点,与一阶泰勒展开法进行了对比实验,实验结果如图7所示. 对比图7(a)和7(c)可以明显看出,一阶泰勒展开法的速度波动率最大值超过5%,绝对平均值为2.01%;而文中算法仅在曲率剧变区域达到0.2%左右,绝对平均值为0.019%.从图7(b)和7(d)可以看出,由于一阶泰勒展开法对参数计算的精度不高,从而导致曲率变化剧烈的区域弓高误差超出允许范围,而文中算法则能很好地控制在精度要求内. 当加工过程中对速度波动率要求较严格时,需要进行1.4节中的插补参数校正.图8展示了采用两种不同方法在满足给定最大速度波动率的条件下,每个插补周期内参数u的校正次数. 由图8(a)可以看出,一阶泰勒展开法大部分的插补周期内参数u的校正次数超过3,在曲率较大的地方校正次数达到5,加工图6所示的NURBS曲线迭代总数为818次(通过对每一个插补周期内迭代次数求和,计算得到迭代总数为818次).图8(b)表明文中算法在曲率变化缓慢的区域无需进行参数校正,在曲率变化最剧烈的地方校正次数仅为3,整个插补过程中迭代总次数为278.实验结果表明基于Runge-Kutta方法的参数值计算更为精确,降低了参数校正过程中的迭代次数,提高了加工效率,验证了文中所提算法的有效性. 图7 文中算法与一阶泰勒展开法对比实验结果 Fig.7 Comparison of experimented results between the proposed algorithm and the first-order Taylor expansion method 图9展示了对上述NURBS曲线采用基于Runge-Kutta方法的插补算法进行插补仿真时,实行进给速度前瞻控制前、后进给速度与加速度的变化趋势. 从图9(a)中可以看出前瞻控制之前,曲线曲率变化急剧的位置基于弓高误差和法向加速度约束自动调整的进给速度变化也很剧烈,而经过前瞻控制之后的进给速度则会提前缓慢减速以及延后缓慢加速.对比图9(b)中的加速度曲线可以看到,实行前瞻控制前,加速度变化剧烈,图9(b)中的G点处,测得加速度a=3.081 1×104mm/s2,远超过机床允许的最大加速度A=2 450 mm/s2.而前瞻控制之后,结合插补参数在区间上的局部放大图9(c)可以发现,机床在加速过程中始终以最大加速度A=2 450 mm/s2加速运行,减速过程中以最大加速度A=-2 450 mm/s2减速运行,满足机床的加减速性能,避免了加速度的剧烈变化,降低了机床受到的冲击. 图8 一阶泰勒展开法与Runge-Kutta法参数u的迭代次数 Fig.8 Iteration number ofuby Taylor expansion method and Runge-Kutta method 图9 进给速度曲线与加速度曲线Fig.9 Feedrate profile and acceleration profile 文中提出了一种基于Runge-Kutta的NURBS曲线实时前瞻插补算法,插补参数采用经典Runge-Kutta方法计算,只需NURBS曲线的一阶导数即可得到高精度的插补参数.粗插补过程中,进给速度根据弓高误差和法向加速度约束进行自动调整,从而满足加工精度;为了降低进给速度波动率,文中设计了一种插补参数校正公式,能快速将速度波动率降低到加工要求的精度范围内.实时精插补过程中对NURBS曲线进行前瞻分段,进而对每个前瞻插补区间进行速度二次规划,避免了速度的急剧变化对机床产生过大的冲击,同时也提高了加工精度. [1] CHEN You-dong,WEI Hong-xing,SUN Kai,et al.Algorithm for smooth S-curve feedrate profiling generation [J].Chinese Journal of Mechanical Engineering,2011,24(2):237- 247. [2] BEDI S,ALI I,QUAN N.Advanced interpolation techniques for CNC machines [J].ASME Journal of Engineering for Industry,1993,115(8):329- 336. [3] SHIPITALNI M,KOREN Y,LO C C.Real-time curve interpolators [J].Computer-Aided Design,1994,26(11):832- 838. [4] YANG DCH,KONG T.Parametric interpolator versus li-near interpolator for precision CNC machining [J].Computer-Aided Design,1994,26(3):225- 234. [5] 孙海洋,范大鹏,李玲.一种参数曲线实时数控插补计算新方法 [J].国防科技大学学报,2008,30(3):122- 127. SUN Hai-yang,FAN Da-peng,LI Ling.A novel method for real-time CNC curved path interpolation calculating [J].Journal of National University of Defense Technology,2008,30(3):122- 127. [6] ZHENG Z Y,YANG C,JING F S,et al.High-precision NURBS interpolation algorithm based on the bisection method [C]∥Proc 34thChinese Control Conference.Hangzhou:IEEE Press,2015:8673- 8677. [7] LIU Q,JIN X J,LONG Y H.A real-time high-precision interpolation algorithm for general-typed parametric curves in CNC [J].International Journal of Computer Integrated Manufacturing,2010,23(2):168- 176. [8] 杜道山,燕存良,李从心.一种实时前瞻的自适应NURBS插补算法 [J].上海交通大学学报,2006,40(5):843- 847. DU Dao-shan,YAN Cun-liang,LI Cong-xin.An adaptive NURBS interpolator with real-time look-ahead function [J].Journal of Shanghai Jiaotong University,2006,40(5):843- 847. [9] 王国勋,舒启林,王军,等.非均匀有理B样条曲线直接插补进给速度规划 [J].计算机集成制造系统,2013,19(6):1272- 1278. WANG Guo-xun,SHU Qi-lin,WANG Jun,et al.Interpo-lation feedrate planning of NURBS [J].Computer Inte-grated Manufacturing System,2013,19(6):1272- 1278. [10] 王允森,杨东升,刘荫忠,等.NURBS插补中的速度规划与参数计算 [J].计算机集成制造系统,2014,20(8):1896- 1912. WANG Yun-sen,YANG Dong-sheng,LIU Yin-zhong,et al.Velocity planning and parameter calculating in NURBS interpolation [J].Computer Integrated Manufac-turing System,2014,20(8):1896- 1912. [11] 施法中.计算机辅助几何设计与非均匀有理B样条 [M].北京:高等教育出版社,2001. [12] PIEGL L,TILLER W.The NURBS book [M].New York:Spinger Verlag,1997:81- 116. [13] 关治.数值分析基础 [M].北京:高等教育出版社,2010:358- 371. [14] JIN Yu-an,HE Yong,FU Jian-zhong,et al.A fine-inter-polation-based parametric interpolation method with a novel real-time look-ahead algorithm [J].Computer-Aided Design,2014,55(3):37- 48. [15] WANG Yun-sen,YANG Dong-sheng,GE Rong-li,et al.Design of trigonometric velocity scheduling algorithm based on pre-interpolation and look-ahead interpolation [J].International Journal of Machine Tools and Manufacture,2015,9(96):94- 105. [16] 刘宇,戴丽,刘杰,等.泰勒展开NURBS曲线插补算法 [J].东北大学学报(自然科学版),2009,30(1):117- 120. LIU Yu,DAI Li,LIU Jie,et al.Study on NURBS interpo-lation with taylor expansion [J].Jounal of Northeastern University(Natural Science),2009,30(1):117- 120. [17] 吴玉香,张景,王聪.基于动态模式的转子系统故障诊断 [J].控制理论与应用,2016,33(4):493- 499. WU Yu-xiang,ZHANG Jing,WANG Cong.Fault diagnosis of rotor system based on dynamical models [J].Control Theory & Applications,2016,33(4):493- 499.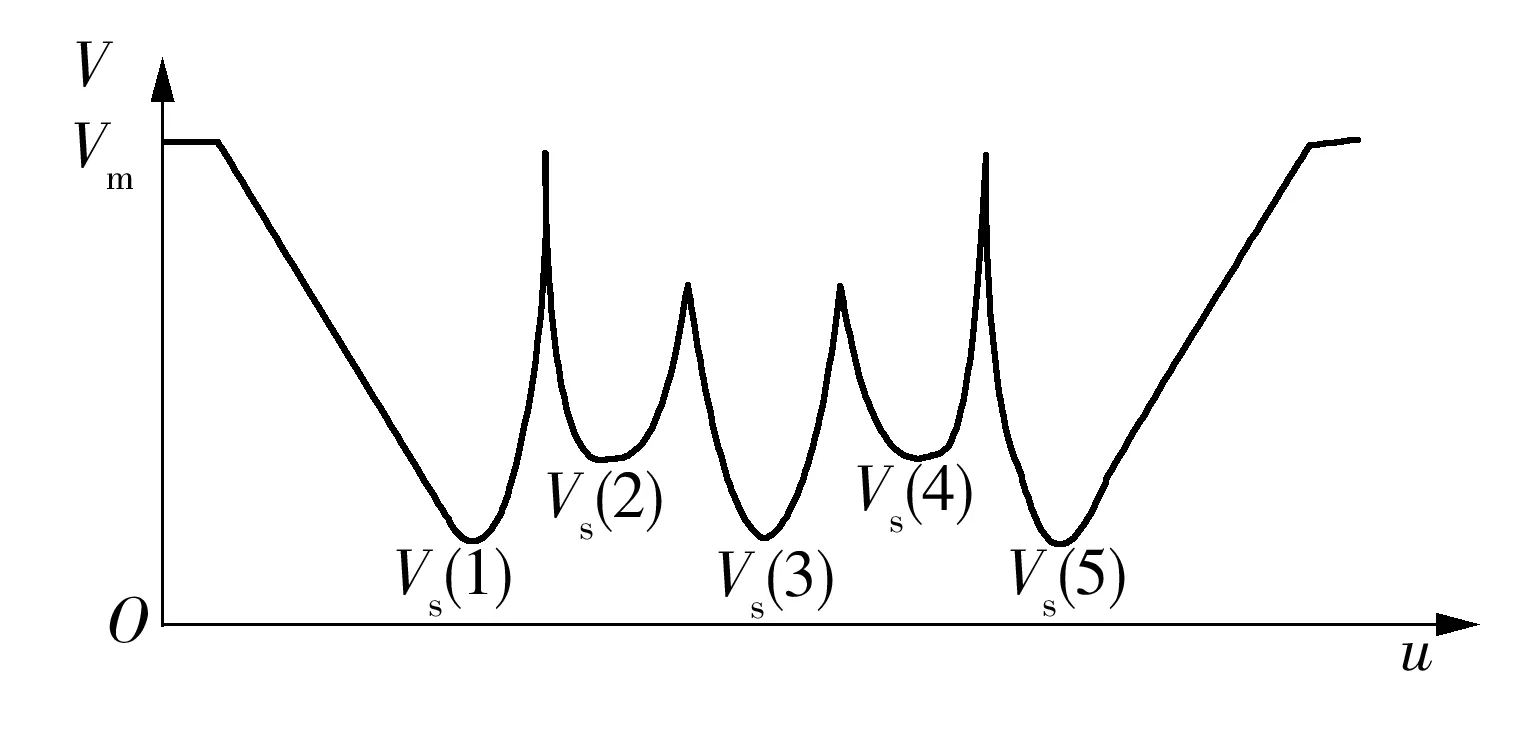
2.2 前瞻距离的确定
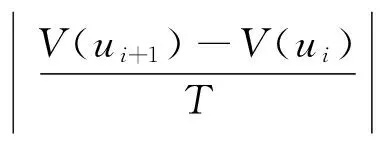
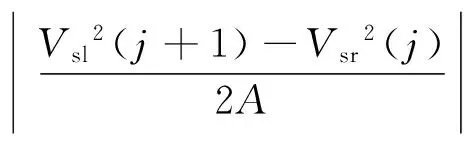
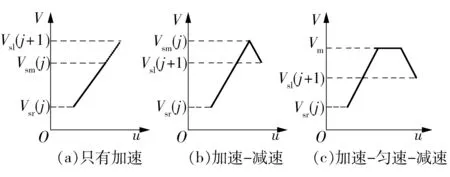
2.3 前瞻插补区间的进给速度二次规划
3 实例仿真分析
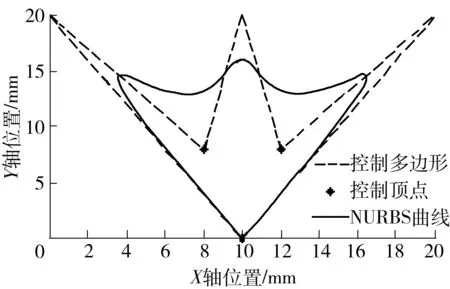
4 结论
