木塑框架结构的可靠性分析

于贵文，李丹婷，程芳超，王 革，林 晶

(哈尔滨商业大学 轻工学院，哈尔滨 150076)

木塑框架结构的可靠性分析

于贵文，李丹婷，程芳超，王 革，林 晶

(哈尔滨商业大学 轻工学院，哈尔滨 150076)

为了分析单跨双层木塑框架结构在实际应用中的可靠性，确定其塑性铰的位置和个数，利用了失效树法确定主要失效机构，根据虚位移理论确定它们的功能函数，分别计算8个主要失效机构的可靠性指标及失效概率.运用相关性分析法确定了该结构体系失效的代表机构，通过概率性网络评价技术计算其失效概率和可靠度，该单跨双层木塑框架结构的可靠度为91%.

木塑板材；框架结构；可靠性分析

木塑复合材料是以聚合物为基体生物质增强的复合材料的俗称[1-6].在实际的应用中，木塑复合材料广泛地应用在建筑业、包装业和园林业，部分地取代了木材[7-9].在室内，木塑板材可以代替木板做家具和地板；在室外，木塑板材被使用在海港铺面板、园林桥梁、园林凉亭、盆景框架等方面.在木塑家具中有许多框架结构，如书架、鞋架等；在园林设计中，也存在诸多框架结构，如园林盆景框架中存在单跨双层框架和多跨多层框架结构.在这些框架结构中，结构不但承载各种死载，还可能承受垂直方向或水平方向的各种随机载荷的作用，这些框架结构可能是多种死载和活载作用的共同体，因此研究这些结构的可靠性，并根据其承受载荷的大小设计它们的结构尺寸，对拓宽木塑复合材料的使用范围，具有十分重大的意义.已有一些学者进行了木塑复合材料的可靠性研究：2003年美国Nian-Zhong Chen等人[10-11]对塑料基复合材料船体进行了可靠性研究，并提出复合加强板材料的极限状态公式；2003年美国Dan M·Frangopola和Sebastien Recek[12]基于蒙特卡罗法分析了层合木塑板材的可靠性；2010年美国Han-Seung Yang等学者[13]对木纤维增强聚乙烯木塑复合材料的疲劳特性和可靠性进行了研究，并提出了木塑复合材料的可靠性分析方法；2000年中国台湾学者S· C· Lin[14]研究了在随机载荷作用下木塑层积材的可靠性； 2011～2012年于贵文、胡英成等[15-17]分别运用一次二阶矩法和改进一次二阶矩法分析了木塑板材的可靠性.至于木塑结构体系的可靠性研究，至今还未发现相关报道.

本研究以挤出成型的木塑复合材料为研究对象，用来制造单跨双层木塑框架结构，通过失效树法确定主要失效机构，通过相关性分析确定代表机构运用概率性网络评价技术(也称PNET法)计算木塑单跨双层框架结构的失效概率.

1 实验材料及方法

1.1 主要试验材料

试验材料为挤出成型聚乙烯基木塑结构板材，其密度为1.29 g/cm3, 木塑比分别为：木粉55% PE45%，试件的横截面尺寸为104 mm×26 mm.

1.2 实验方法

通过三点弯曲试验获得各试件的最大弯曲力、静曲强度和断裂曲线.通过简单的计算得到其最大

抗弯力矩，并设定单跨双层木塑框架结构上所承受相应载荷的大小，从而分析该结构的可靠性.

2 木塑单跨双层结构实例

木塑单跨双层框架结构，其受力情况和具体结构如图1所示，

通过静态弯曲试验获得各木塑板件的最大弯曲力、静曲强度和断裂曲线.通过简单的计算得到其最大抗弯力矩，并设定相应载荷的大小，从而分析该结构的可靠性.

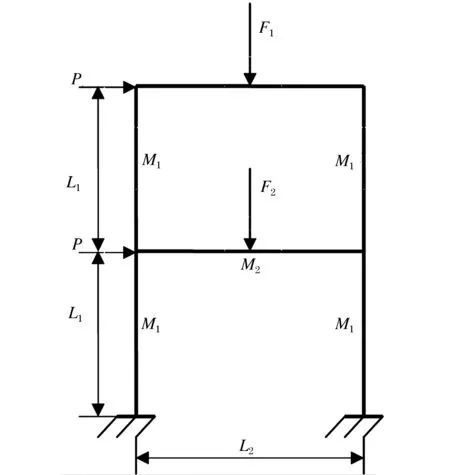
图1 木塑框架结构简图

参数F1/NF2/NP/NM1/(N·m)M2/(N·m)L1/mL2/m均值200300801201501．201．60标准差3040202030

3 可靠性分析

3.1 塑性铰分析及失效概率计算

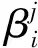
图2 塑性铰分析图

根据表2中各个主要失效机构的功能函数，计算各个主要失效机构的失效概率可根据式(1)、(2)计算，具体计算结果列于表3中.

(1)

pfk=Φ(βk)

(2)

表2 塑性铰的功能函数

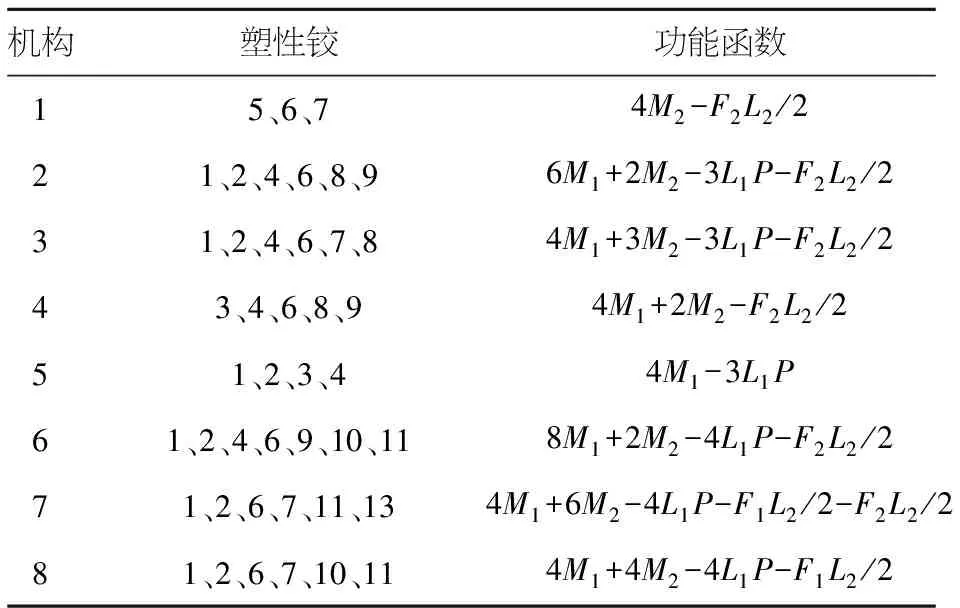
机构塑性铰功能函数15、6、74M2-F2L2/221、2、4、6、8、96M1+2M2-3L1P-F2L2/231、2、4、6、7、84M1+3M2-3L1P-F2L2/243、4、6、8、94M1+2M2-F2L2/251、2、3、44M1-3L1P61、2、4、6、9、10、118M1+2M2-4L1P-F2L2/271、2、6、7、11、134M1+6M2-4L1P-F1L2/2-F2L2/281、2、6、7、10、114M1+4M2-4L1P-F1L2/2

表3 功能函数的失效概率

机构βiPfi12．900．00595323．160．00270734．760．000004844．910．000002351．800．0789563．360．00141173．540．00758182．820．007483

3.2 主要失效机构间的相关性分析

为了选择单跨双层木塑框架结构失效的代表机构，首先应分析各机构之间的相关系数，各机构之间的相关系数可根据各个主要失效机构的功能函数通过式(3)、(4)计算，各个主要失效机构之间的相关系数列于表4中.

ρzi,zj=cov(zi,zj)σziσzj=

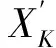
(3)

(4)

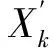
表4 主要失效结构之间的相关系数

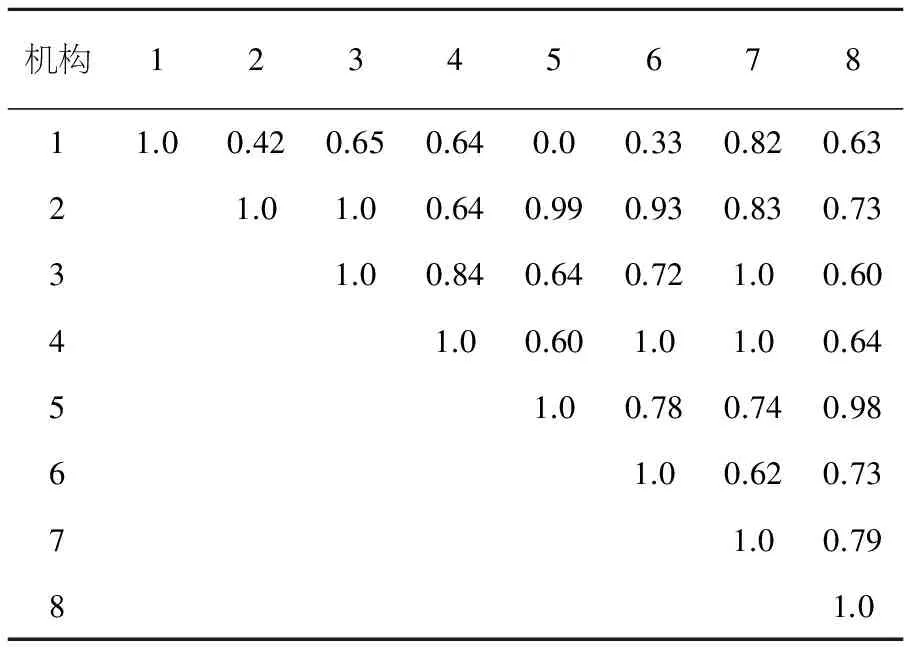
机构1234567811．00．420．650．640．00．330．820．6321．01．00．640．990．930．830．7331．00．840．640．721．00．6041．00．601．01．00．6451．00．780．740．9861．00．620．7371．00．7981．0

3.3 基于PNET法的可靠性分析

概率性网络评价技术法(也称PNET法)， PNET法计算结构体系的可靠度程序如图3所示，可通过式(5)计算该结构的失效概率：

Pf=∑mi=1Pfk(k=1,2,…,8)

(5)

其中：m是相关系数小于相关系数定限值(ρ0=0.6)的机构数，Pfk是各机构的失效概率，Pf是该结构的失效概率.

按照程序框图3的步骤，结合表3各个主要失效机构的失效概率值，当ρo=0.6时，该框架结构的主要失效机构1、2、5、6为代表机构，根据式(5)计算木塑框架结构体系的失效率：Pf=Pf1+Pf2+Pf5+Pf6=0.089，即木塑框架结构体系的可靠度为91 %.

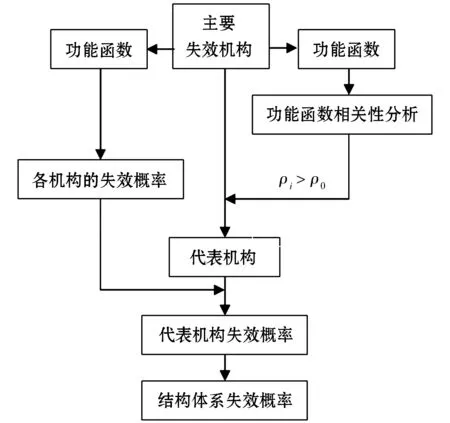
图3 PNET法程序框图

4 结 论

通过对单跨双层木塑框架结构的可靠性计算与分析得到以下结论：

1)通过对单跨双层木塑框架结构产生塑性铰进行分析，确定了8个主要失效机构.

2)经过各个主要失效机构之间的相关性分析，确定1、2、5、6为单跨双层木塑框架结构失效的代表机构，这4个代表机构决定了该结构的失效概率.

3)运用概率性网络评估技术计算该结构的失效概率，其可靠度为91%.

[1] 于春贺, 陆绍荣, 阳志有, 等. 超分散剂对SF/PP木塑复合材料结构与性能的影响[J]. 材料导报, 2011, 25(17): 405.

[2] 朱明源, 易红玲, 林 珩. 木塑复合材料的力学性能、微观结构与流变性能的研究[J]. 塑料工业, 2013, 41(2): 74-78.

[3] 王宝云, 陈 伟, 杨 柳, 等. PVC/PE基木塑复合材料性能研究[J]. 塑料工业, 2011, 39(2): 29-36.

[4] 张求慧, 张 晶, 刘 娟. 我国发泡木塑复合材料的研究现状及进展[J].材料导报, 2014, 28(3): 85.

[5] 郑景新, 庞 浩, 陈 永, 等. 木塑复合材料的研发与进展[J]. 化学建材, 2008, 24(3): 1-4.

[6] 李自强. 木塑复合材料制备及性能研究[D]. 济南: 山东大学, 2009. 1-21.

[7] 马建立, 赵由才, 任天斌, 等. 利用废旧PE/PP制备木塑复合材料的研究[J]. 塑料工业, 2007, 35(8): 57-59.

[8] DEFOIRDT N, GARDIN S, BULCKE J V,etal. Moisture dynamics of WPC and the impact on fungal esting [J]. International Biodeterioration Biodegradation, 2010, 64: 65-72.

[9] WECHSLER A, HIZIROGLU S. Some of the properties of wood plastic composites[J]. Building and Environment, 2007, 42: 2637-2644.

[10] CHEN N Z, SUN H H, SOARES C G. Reliability analysis of a ship hull in composite material [J]. Composite Structures, 2003, 62: 59-66.

[11] CHEN N Z, SOARES C G. Reliability assessment of post-buckling compressive strength of laminated composite plates and stiffened panels under axial compression[J]. International Journal of Solids and Structures, 2007, (44): 7167-7182.

[12] FRANGOPOLA D M, EBASTIEN R. Reliability of fiber -reinforced composite laminate plates [J]. Probabilistic Engineering Mechanics, 2003 (18): 119-137.

[13] YANG H S, QIAO P Z, WOLCOTT M P. Fatigue characterization and reliability analysis of wood flour filled polypropylene composites [J]. Polymer Composites, 2010, 10: 554-560.

[14] LIN S C. Reliability predictions of laminated composite plates with random system parameters [J]. Probabilistic Engineering Mechanics, 2000(15): 327-338.

[15] HU G W. Reliability analysis of wood-plastic structural planks with different density [J]. Packaging Engineering, 2011, 32(9): 9-11.

[16] 于贵文, 胡英成. 木塑结构板材的可靠性预测[J]. 复合材料学报, 2013, 30(2): 254-259.

[17] 于贵文, 李丹婷, 常 江, 等. 结构增强木塑板材的力学性能无损检测[J]. 工程塑料应用, 2011, 39 (3): 63-65.

Reliability analysis for single-span two-story wood plastic construction

YU Gui-wen, LI Dan-ting, CHENG Fang-chao, WANG Ge, LIN Jing

(School of Light Industry, Harbin University of Commerce, Harbin 150028, China)

In order to analyze the reliability of one-span two-story wood plastic frame construction in practical application, first, the position and number of plastic hinge were determined. The fault tree analysis method was used to determine 8 main failure mechanisms. The functions of them were determined according to the virtual displacement theory, and the failure probability of functions was calculated. The reliability indexes of the 8 main failure mechanism were calculated, and the represent mechanisms of the structure system were determined using the correlation analysis method. The probabilistic network evaluation technique was used to calculate the failure probability and reliability. The reliability of the single-span two-story wood-plastic frame construction was 91.1%.

wood-plastic planks; frame construction; reliability analysis

2016-05-24.

黑龙江省教育厅科技项目(12541207).

于贵文(1967-)，男，博士，教授，研究方向：木质基复合材料及其力学性能研究.

TB332

A

1672-0946(2017)01-0066-03