一线串起课堂

吕 娟

（江苏省南京市伯乐中学，江苏南京 210038）

引 言

《义务教育数学课程标准（2011年版）》指出：“学生是数学学习的主人，教师是数学学习的组织引导者。”刚接到教研员老师通知我要开设一节关于角的复习课时，我的心里很慌。角这个部分的知识点很多，一课时的复习很“拥挤”。如何安排这节课的复习，例题的选择、练习的筛选都是我要考虑的问题。在备课一稿时，我选择了最保守的思路：第一部分是自主学习，选取六道小题（选择题和填空题），题目难度较小，目的是让学生通过完成小题来复习角这一章的知识点，完成知识框图的建立；第二部分是交流展示，主要选取了三道例题。例1的设计目的是考查角的和差关系以及等式的基本性质的综合应用。例2的设计目的是考查邻补角的定义，以及根据题中给出的等量关系列出方程，灵活运用方程的方法解题。例3主要考查角平分线的性质和平角的知识。在三道例题后，我选择了一道拓展延伸题，主要考查学生对角的计算的理解和掌握。

试上了一节课后，我发现效果一般，知识点太琐碎、题量大，学生思考的时间长，影响课堂进度。

一、案例描述

在毫无头绪之时，我想到了三大终极问题：“我是谁，从哪儿来，到哪儿去。”此时，一个念头划过。对，角是怎么产生的？两条直线相交产生。整节课不就是围绕一些角、线而展开的吗?于是，我开始这样处理这节课，抛弃前面的PPT课件，改用几何画板来完成课堂教学，只为体现从一变多的过程。

师：平面内两条直线的位置关系有几种？生：（全员回答）平行与相交。师：很好，今天我们来研究直线相交的相关问题，首先我们看活动一。

活动一 ：如图1，直线AB、CD相交于点O，形成四个角，那么这四个角有何关系？

图1

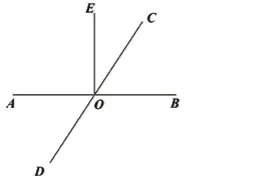
图2

图3

图4

生：（迅速回答）对顶角相等，互为补角的两个角的和是180°。师：非常好，反应很快。（在黑板上补上结构框图中的“补角、对顶角”以及对顶角相等）如果我在图上再加一条射线OE呢？（在几何画板上按下OE按钮）若∠BOE=90°,则∠BOC与∠COE有何关系？生：（不假思索）∵∠BOE=90°，∴∠BOC+∠COE=90°，∴∠BOC与∠COE互余。师：对的，这就是余角的定义。（在黑板上补上结构框图中的“余角”）若我在这个图上再加上一条射线，会发生什么？若OF⊥CD，则∠AOF与∠COE有何关系？请说明理由。生：（眼睛里满是好奇）思考……师：能不能想想这题和刚才的题有何联系？垂直能想到什么？生：（部分稀疏的声音）90°。师：对的，90°能想到哪个知识点？生：余角。师：和∠AOF、∠COE有关的有几对余角呢？生：∠AOF+∠EOF=90°，∠COE+∠EOF=90°。生：哦……∠AOF=∠COE。师：为什么呢？生：（异口同声）同角的余角相等。师：非常好！这条性质还可以继续补充，应该是……生：（全班齐答）同角（等角）的余角（补角）相等。师：正确！（在黑板上补上结构框图中的“同角[等角]的余角[补角]相等”）回到图1，添上另一条射线OP，我们来看活动二。

活动二：直线AB、CD相交于点O，若∠AOC=130°，OP平分∠BOC，求∠POC的度数。

师：怎么思考这道题？要求∠POC，只要求……生：(极少数)要求∠BOC。师：对，∠BOC也是未知的，怎么求？生：我知道。∠BOC是∠AOC的补角，等于180°减去130°，也就是50°。师：很好，在做几何题的过程中，就是要熟练地使用综合法和分析法解题。同时，要注意书写（补充板书中的结构框图“角平分线”，板书解题过程）至此，本节课的知识框图全部完成。师：图4中，我们只有一条角平分线，如果再……生：再加一条对角线（很是兴奋）。师：很聪明，已经知道老师的套路了。若OQ平分∠AOC，求∠POQ的度数。

图7

图5

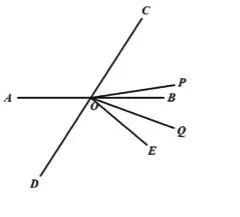
图6

图8

随后给出变式：直线AB、CD相交于点O，OP、OQ分别平分∠BOC,∠AOC，求∠POQ的度数。

活动三：直线AB、CD相交于点O，∠BOC=α，∠BOE=β(β为锐角)，OP、OQ分别平分∠COE，∠BOE,求∠POQ的度数。

拓展提升：已知∠AOB=110°，∠BOC=40°，OP、OQ分别平分∠AOB,∠BOC，求∠POQ的度数。

关于拓展提升的处理，我让学生自己完成作图，主要考查角的计算。做题时，部分学生没有分类讨论。此题是对本节课的一个提升。

二、案例反思

对两条直线相交的基本图形的变形，是这次课堂教学中较成功的一笔。就是因为这一探索过程，对于我补充的练习属中等难度的题型，班级中成绩偏下的学生也能很好地掌握。而对于拓展提升练习，对于初学几何的学生来说，难度有点大。一部分学生显露出感兴趣的神情，不少学生能很好地解答此类题。能够达到如此好的效果，完全因为摒弃了常规的独立例题，找到了一条神奇的线索，串起了整节课。

关于这节复习课，我有以下几点想法。

1.剥茧抽丝，抓住重点

复习课不像新授课那么“新鲜”，而且内容丰富，抓手太多，导致无从下手。从知识层面上说，教师应思考的问题有以下几点：初中阶段的数学知识有哪些？在这些知识中，哪些是核心概念？核心的数学思想方法是什么？中考的重点、热点、难点是什么？教师要做的就是剥茧抽丝，从中抓住重点[1]。

2.找到线索，化难为易

抓住重点后，教师还应思考如何呈现知识，如何引领学生学会整理与归纳所学知识。化重点为线索，从一个基本图形出发，讲解一个知识点，之后不断地对基本图形进行变形，全面覆盖知识点，突出重点内容。一题多变，让一节课用一条线索串联以来，使得教学的每个环节都不再是彼此独立的部分。一节课环环相扣，循序渐进，步步逼近课程教学目标。一条线索串起课堂，借助一题多变，促进学生探索能力的提高，学生的解题思路得到拓展，解题能力得到提高。一条线索串起课堂，化难为易，实现深入浅出。

3.重视综合，融会贯通

数学复习要注意基本概念、定律、公式的比较以及应用，从具体到抽象等多层次、多维度、全方面地融会贯通。对于几何复习，应弄清来龙去脉，理清相互关系，注意表达形式，使每一个知识点联系起来，达到以点成线、以线成面、以面成体的目的[2]。

[1] 中华人民共和国教育部.义务教育数学课程标准[M].北京:北京师范大学出版社, 2011.

[2] 张文镇.提高初中数学课堂分层教学效果的策略探析[J].中学生数理化(学研版),2013,(05):27.