考虑滴头堵塞位置的灌水均匀系数模型优化
2017-03-04张若婵牛文全段晓辉
张若婵,牛文全,2,,※,段晓辉,李 元
考虑滴头堵塞位置的灌水均匀系数模型优化
张若婵1,牛文全1,2,3,※,段晓辉3,李 元3
(1. 西北农林科技大学水利与建筑工程学院,杨凌 712100;2. 中国科学院水利部水土保持研究所,杨凌 712100;3. 西北农林科技大学水土保持研究所,杨凌 712100)
为准确评价堵塞对滴灌工程灌水均匀性的影响,从确定采样点布置方式入手,利用HYDRUS-2D模拟不同堵塞情况下的土壤水分状况,首先分析灌水均匀性与土壤水分分布均匀性之间的关系,然后以土壤水分分布均匀系数为依据,在考虑滴头堵塞位置的基础上对灌水均匀系数模型进行优化,最后通过温室灌溉试验进行验证。结果表明,取样点布置方式对土壤水分分布均匀系数影响显著,适宜的取样间距和深度分别为60 cm及地表下20 cm。土壤水分分布均匀系数与不同灌水均匀系数之间存在良好的线性关系,且随着堵塞滴头数量的增加,堵塞滴头位置分布情况对土壤水分分布均匀性的影响增大。小区灌溉试验结果表明,当堵塞滴头数量较多时,土壤水分分布均匀系数与考虑滴头堵塞位置的优化灌水均匀系数具有较高的相关性,优于原指标,可较好反映由堵塞滴头位置改变引起的土壤水分分布均匀性变化,故在评价滴灌系统灌水均匀性时宜使用优化均匀系数。
土壤水分;灌溉;优化;滴头堵塞;灌水均匀性;土壤水分分布均匀性;堵塞位置
0 引 言
灌水均匀性是滴灌系统设计和评价的重要控制指标,灌水均匀性一般用灌水均匀系数和流量偏差率表示。灌水均匀系数,如克里斯琴森均匀系数[1]主要反映灌水器流量的相对平均偏差;Criddle等[2-3]提出用分布均匀系数来描述水量分布均匀性,有利于保证作物获得必要的灌水量;Keller等[4]综合考虑灌水器流量偏差、制造偏差的组合效应,提出了凯勒均匀系数;随后,许多学者对凯勒均匀系数进行了改进,使其对灌水均匀性的评价更为准确[5-10]。滴灌系统的设计常以流量偏差率为参考依据。Wu等[11]最先在讨论流量偏差范围时指出,灌水器流量的均匀性可以简单地用灌水器的流量偏差来表征,并提出了灌水器流量偏差率的计算公式;Bralts等[12]考虑灌水器的水力偏差和制造偏差,通过统计学方法计算出灌水器流量偏差系数,并据此提出了统计均匀系数;Howell等[13]主要考虑水力偏差提出了流量偏差率和水力偏差率;郑耀泉[14-15]通过模拟计算建立了微灌灌水均匀系数与总的灌水器流量偏差系数、流量偏差率及灌水器水力偏差率之间的关系;张国祥[16-17]、牛文全等[18]、张林等[19-21]、朱德兰等[22-24]综合考虑了水力偏差、制造偏差和地形偏差的影响,提出了更为可靠的流量偏差率计算公式。
上述2类评价指标均以滴头流量的平均偏差为基础,仅考虑滴头流量的变化,忽略了堵塞滴头位置分布对灌水均匀性的影响。调查和试验发现,一般情况下,滴灌系统经过一段时间运行后,毛管尾段滴头极易发生集中堵塞[25]。为此,牛文全等[26]在克里斯琴森均匀系数的基础上,提出了考虑滴头堵塞位置的灌水均匀性评价指标,并假设滴头流量分布均匀性和堵塞滴头位置分布均匀性所占比例相当。
目前,灌水均匀性评价指标尚不统一,评价结果差异较大,需建立一个较为客观的标准,为灌水均匀系数设计提供依据。土壤水分分布均匀性是判定灌水是否均匀的最直接表征,故本研究在明确取样点合理布设方式的基础上着重探讨灌水均匀性与土壤水分分布均匀性之间的关系,先建立二者的回归模型,分析常用的灌水均匀系数之间的差异,再对考虑滴头堵塞位置的灌水均匀系数进行优化,为合理评价滴灌系统的灌水质量提供依据。
1 材料与方法
1.1 滴头堵塞状况设置
从滴头平均堵塞程度(堵塞滴头流量的平均减少量与设计流量之比)、堵塞滴头占比(堵塞滴头数量占滴头总数的比例)及堵塞滴头位置分布3方面考虑,采用完全组合设计,共设置了27种堵塞状况。其中,滴头平均堵塞程度设置40%、60%、80%共3个水平,堵塞滴头占比设置10%、20%、30%共3个水平,堵塞滴头位置分布设置集中(集中分布在1个区域)、较集中(集中分布在2个区域)、均匀分布共3种情况(如图1所示)。

图1 堵塞滴头在研究小区分布示意图
1.2 滴灌毛管铺设方式
模拟灌水小区内,毛管按图2所示方式铺设,长度均为60 m,毛管间距设置为50 cm,共铺设10条毛管。毛管上滴头间距为30 cm,滴头额定流量设置0.9和2.0 L/h共2个水平。
沿毛管方向从第1个滴头处、垂直毛管方向从模拟小区边界处开始设置观测点。观测点间距(毛管方向×垂直毛管方向)分别为30 cm×30 cm、60 cm×60 cm(如图2所示)、90 cm×120 cm,矩形网格布置。通常情况下,作物根系主要分布于地表以下0~30 cm的区域,该区域内土壤水分分布情况会直接影响到作物的生长[27],故每个点位分别模拟地表以下10、20、30 cm处的土壤含水量。

注:数值的单位为cm,下同。
1.3 评价指标
1.3.1 土壤水分分布均匀系数
土壤水分分布均匀性通常采用以土壤含水量为计算基础的克里斯琴森均匀系数来表示[27]。
式中C为土壤水分分布均匀系数;为平均土壤含水量,cm3/cm3;为第个取样点的土壤含水量,cm3/cm3;为观测点总数。
1.3.2 灌水均匀系数
通常采用克里斯琴森均匀系数[1]和凯勒均匀系数[4]表示灌水均匀性。
式中C为克里斯琴森均匀系数;q为第个滴头的流量,L/h;为所有滴头的平均流量,L/h;为滴头总数;E为凯勒均匀系数;25%为将滴头流量从小到大排列后占滴头总数1/4的流量低值的平均值。
以上2个常用指标仅考虑流量的影响,牛文全等[26]定义了堵塞滴头位置分布均匀系数,并在此基础上提出了考虑滴头堵塞位置的灌水均匀系数。
式中R为堵塞滴头位置分布均匀系数;r为第个计算区域的大小;为所有计算区域大小的平均值;为计算区域的个数;为考虑滴头堵塞位置的灌水均匀系数。
1.4 HYDRUS-2D模拟滴灌条件下土壤水分的方法
1.4.1 土壤水分运移基本方程
假设土壤是各向同性、均质的刚性多空介质,忽略温度、空气以及滞后效应的影响,土壤水分运动可用Richard方程来描述[28]:
式中、、分别为三维坐标,cm,规定向下为正;为时间,min;为土壤体积含水量,cm3/cm3;()为非饱和导水率。
1.4.2 模拟试验设计
本研究假设每个滴头的出流状况仅能影响其相邻滴头处的土壤水分状况,并根据观测点布置方式,模拟垂直毛管方向上(图3)3个相邻滴头在6种堵塞情况(用1表示未堵塞滴头,0表示堵塞滴头,这6种情况分别为a:111,b:110(与011相同),c:100(与001相同),d:101,e:010和f:000)下进行灌溉后的土壤水分状况,代表模拟小区内发生相同堵塞状况的滴头附近的土壤水分状况。

注:ODFE为模拟算区域;A、B、C分别为滴头所在位置;x为垂直毛管方向;z沿土壤深度方向。
1.4.3 定解条件
图3给出了土壤水分运动数值模拟区域示意图,其中(25,0),(75,0),(125,0)分别为3个滴头所在位置。
1)初始条件:
(,,)0(0, 0,0) (7)
式中0为土壤初始含水量,cm3/cm3;为模拟区域的横向最大距离,取150 cm;为模拟区域的纵向最大距离,取60 cm。
2)边界条件:
为模拟计算区域的上边界。受到灌水的影响(不考虑降雨和蒸发),滴头周围会形成1个水量饱和区域,应分段考虑。以滴头附近的区域为例,
θ=θ(0<-25<R,=0,>0) (8)
-()+()=0(R<-25
式中R为饱和区半径;θ为土壤饱和含水量。
确定饱和区半径时,可认为滴头流量等于土体增加水量与时间的比值,故先假设R为定值,再分析R与之间的关系[29]。
EF为下边界,假设地下水埋深较大,无水量补给,故设定为自由排水边界,即
OE和DF分别为左、右边界,由于滴头流量无法达到该位置,该处流量进出平衡,故左、右边界设定为零通量边界。
1.4.4 模型求解
利用软件HYDRUS-2D对数学模型进行数值求解。模拟区域为1个长(垂直毛管方向)150 cm、宽(纵向)60 cm的矩形区域(如图3所示)。采用三角形网格(3.5 cm)进行划分求解,并在滴头处适当进行网格加密。模拟总时长为72 h,其中灌水时长为10 h。经过62 h的再分布后,土壤内的水分状况已相对稳定,故不同堵塞情况下的土壤水分分布具有可比性。模拟计算采用变时间步长,初始步长为1 min,最小步长为0.01 min,最大步长为60 min。
1.4.5 模型验证方法
1)试验材料
为了验证数值模拟结果的可靠性,用土箱模拟滴灌的方法进行了验证试验。供试土壤采自陕西省咸阳市杨陵区渭河三级阶地,取土深度为0~40 cm。土样去杂质后风干碾压并过筛备用。土壤密度为1.36 g/cm3,初始含水率为0.0795。土样由不同粒径的颗粒组成,其中砂粒、粉粒和黏粒所占质量分数分别为22.6%、62.1%和15.3%。采用Van Genuchten模型对土壤水分特征曲线()和非饱和土壤导水率()进行拟合。
式中θ为土壤饱和含水量,cm3/cm3; K为土壤饱和导水率,cm/min;θ为土壤残余含水量,cm3/cm3;S为有效含水率(饱和度);为孔隙连通性参数,一般取0.5,、和为经验参数。本研究中,θ=0.406 cm3/cm3,θ= 0.0607 cm3/cm3,K=0.0186 cm/min,=0.0049,=1.6857。
2)试验装置及方法
试验装置如图4所示,由马氏瓶、滴头及试验土箱组成。用医用注射针头模拟滴头,马氏瓶供水。试验土箱由有机玻璃加工而成,其长、宽、高均为50 cm,可观测灌水过程中水分在水平和垂直方向的运移情况。
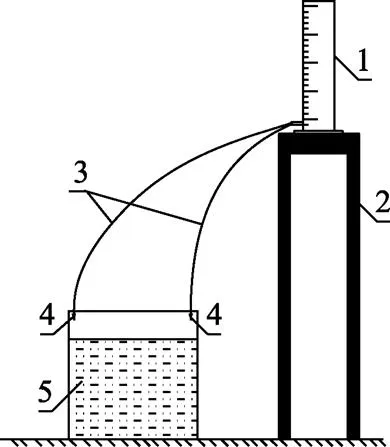
1.马氏瓶 2. 活动支架 3. 医用输液管 4. 滴头 5. 试验土箱
试验前,将风干过筛土按设定容重(1.36 g/cm3)分层装填,每层厚度5 cm,共装填8层,层间打毛。本试验采用2个滴头进行滴灌,分别布置在试验土箱同一侧的两角,滴头间距为50 cm。滴头流量为0.225 L/h,通过医用注射针头上的滚轮来调节。试验取滴灌湿润体的1/4作为研究对象,故实际滴灌流量相当于0.9 L/h[24]。试验时土箱上表面用塑料纸覆盖以防止蒸发。
在入渗过程中,用卷尺测量各时间点湿润体水平和垂直湿润距离。试验总时长为72 h,灌水时长为10 h。试验结束后,在滴头及距滴头15 cm处用土钻分层取样,用烘干法测定所取土样的含水率。
1.5 考虑滴头堵塞的灌水均匀系数模型的验证方法
1.5.1 试验田概况
为明确考虑滴头堵塞位置的灌水均匀系数在工程中的适用性,于日光温室内进行验证试验。试验温室位于108°02¢E、34°17′N,海拔高度460 m。试验地所处位置属暖温带半湿润大陆性季风气候,年平均温度约为16.1 ℃。试验土壤为壤土,土壤质地均匀,随深度没有明显变化,其中砂砾、粉粒、黏粒所占质量分数分别为25.4%、44.1%、30.5%,土壤平均初始含水率为0.137。
1.5.2 试验设计
试验考虑堵塞滴头占比(堵塞滴头数量占滴头总数的比例)及堵塞滴头位置分布2个因素。试验中堵塞滴头占比设置20%和30% 2个水平(简记为A1和A2),堵塞滴头位置分布设置“均匀分散”、“较分散”和“集中分布于毛管尾部”3个水平(如图1所示,简记为B1、B2和B3)。采用完全组合试验设计,共6个处理。试验小区尺寸为2.5 m10 m,2个小区之间留0.3 m的缓冲区,以防止小区间可能发生的水分交换。各试验小区均按图5所示方式布置,南侧毛管距小区南边界以及毛管首端距小区西边界均为50 cm,毛管间距为50 cm,共布置4条毛管,毛管上滴头间距为30 cm,每条毛管长900 cm。滴头流量通过管道首部的阀门控制,经测定正常滴头平均流量为1.51 L/h,堵塞滴头通过在滴头处涂抹强力胶来实现,其流量为0。灌水时长为10 h。

注:A1、A2分别表示堵塞滴头数量占滴头总数的比例为20%和30%;B1、B2、B3分别表示堵塞滴头均匀分散、较分散和集中分布于毛管尾部。
以灌水结束后62 h土壤水分状况为研究基础,沿毛管方向从小区西边界向内50 cm处、垂直毛管方向从小区南边界向内40 cm处开始设置采样点,纵向及横向采样间距均为60 cm。用土钻取土,取样深度为地表下15~20 cm。用烘干法测定土壤含水量。
2 结果与分析
2.1 HYDRUS-2D模型验证结果
2.1.1 滴头处水平垂直湿润距离随时间变化
图6为灌水过程中,滴头处水平和垂直湿润距离随时间的变化。在整个灌水过程中,土壤水分水平运移距离的实测值略大于模拟值,而垂直运移距离的实测值略小于模拟值,但整体而言,这2个方向上湿润距离的模拟值与实测值之间的差异均较小,平均相对误差仅为7.45%和9.31%。对这2个方向上运移距离的实测值和模拟值进行线性拟合后,2分别为0.982和0.996(<0.01),接近于1。可见,土壤水分运动的模拟值与实测值吻合较好,说明采用模拟试验能较好地描述滴灌过程中湿润距离随时间的变化情况。

图6 水分运移距离与时间的关系
2.1.2 灌水62 h后土壤含水量分布
图7为灌水结束62 h后,滴头及水平方向上距滴头15 cm处,土壤含水量随深度变化过程。滴头位置处土壤含水量模拟值随土壤深度变化趋势与实测结果几乎完全一致,距滴头15 cm处二者的偏差相对较大,但平均相对误差均保持在4%左右。对土壤含水量实测值与模拟值按照线性拟合后,2分别为0.967和0.999(<0.01),接近于1。因此模拟计算结果具有较高的精度,也能较好地描述滴灌过程中土壤水分的分布状况。

图7 土壤含水量模拟值与实测值比较
从湿润距离和土壤含水量2个方面,都可以说明该模拟结果的可靠性,故可以利用该模型模拟不同堵塞情况下土壤水分分布状况,并在此基础上分析灌水均匀性与土壤水分分布均匀性之间的关系。
2.2 考虑滴头堵塞的灌水均匀系数模型的建立
2.2.1 采样点布置方式及取样深度对土壤水分分布均匀性的影响
分别计算滴头额定流量为0.9 L/h时,各取样点布置方式下土壤水分分布均匀系数(表1)。由表1可看出,土壤水分分布均匀系数值随着取样间距增大而增大。多重比较结果表明30 cm×30 cm及60 cm×60 cm取样间距下的C之间无显著差异,但均与取样间距为90 cm×120 cm时的C差异较大。90 cm×120 cm的取样间距过大,土壤水分分布均匀系数被过高估计,不具有代表性;而30 cm×30 cm的取样间距过小,取样工作量过大,故60 cm×60 cm是适宜的取样间距。
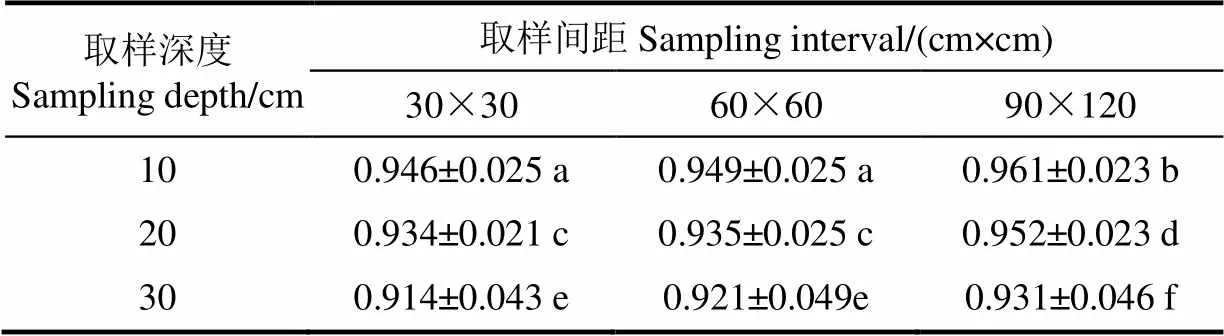
表1 各取样位置下土壤水分分布均匀系数Cuw
注:不同小写字母表示在0.05水平上处理间差异显著。
Note: Different letters indicate significant difference among treatments at 0.05 level.
从表1还可看出,不同取样深度下的C之间存在显著差异。若模拟土壤为均质、各向同性的多孔介质,在本文设定的土壤状况及流量下,水分入渗深度约为27 cm。表层至10 cm深度处土壤水分供给充足,即使部分滴头发生堵塞,灌溉水仍能以土壤为媒介,渗透至土壤表层,并发生交汇现象,在表层土壤处沿毛管形成湿润带,使得土壤水分分布均匀性被高估;而对于30 cm土层来说,由于水分入渗深度较小,该处土壤含水量均为初始含水率,故土壤水分分布均匀性存在被低估的可能,亦不具有代表性。因此在本文设定的灌水及土壤状况下,可以选用地表下20 cm处的土壤含水量计算土壤水分分布均匀系数。
2.2.2 灌水均匀系数与土壤水分分布均匀系数的关系
取样间距为60 cm×60 cm、取样深度为20 cm时,分别对2种滴头流量下各堵塞情况的土壤水分分布均匀系数与1.3.2中各灌水均匀系数进行回归分析并建立回归模型。
C=a·C+b
C=a·E+b
C=a·C+¢·R+b(14)
式中a、a、a、¢分别为各回归模型中C、E、C、R的系数;b、b、b分别为各回归模型中的常量。
决定系数2反映回归模型的拟合效果,其值越大,模型拟合效果越好。表2中多数回归模型的2基本维持在0.7以上,拟合效果良好。回归方程的显著性检验结果也表明,土壤水分分布均匀系数与灌水均匀系数具有显著的线性关系,因此利用土壤水分分布均匀系数来评判各灌水均匀系数是合理的。
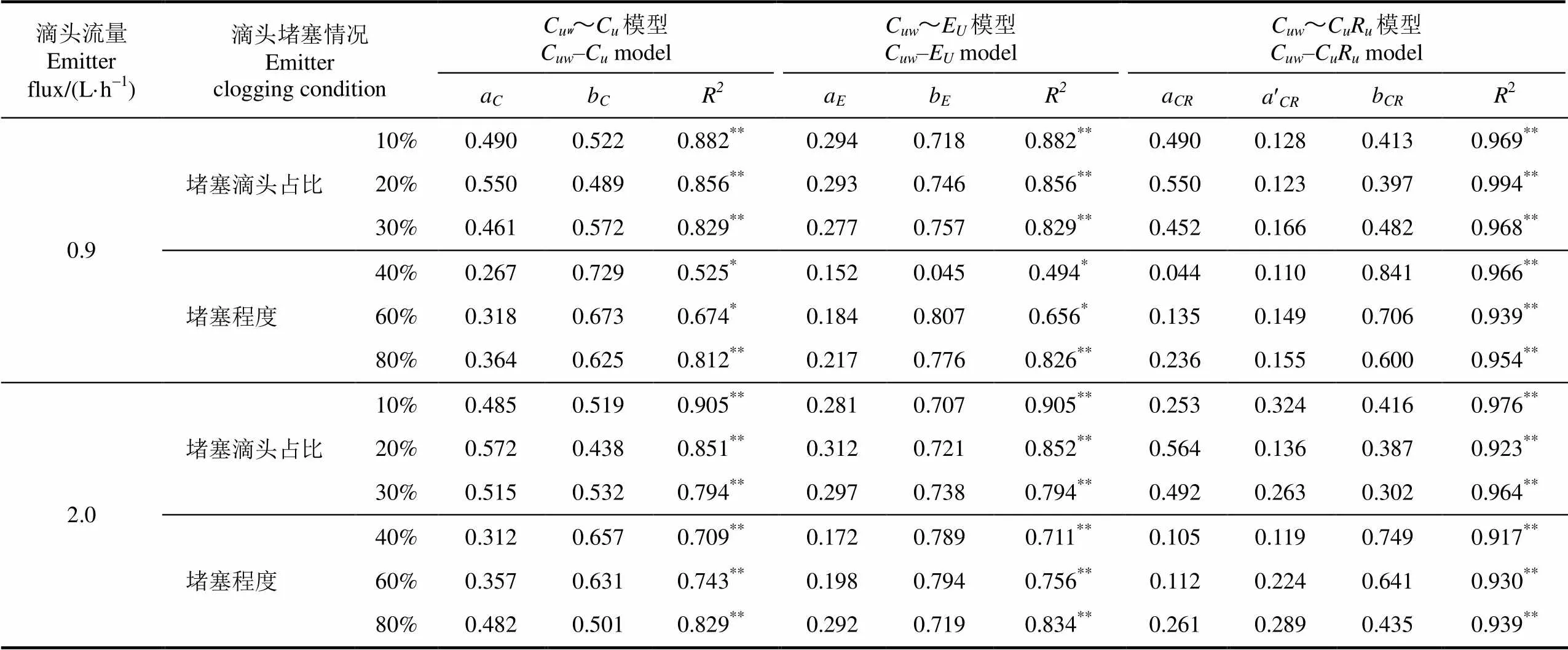
表2 土壤水分分布均匀系数Cuw与各灌水均匀系数的线性回归模型
注:“堵塞滴头占比”为堵塞滴头占滴头总数的百分比;“堵塞程度”为堵塞滴头减少的流量与设计流量之比;a、a、a、′为回归系数,b、b、b为回归模型中的常量; C为克里斯琴均匀系数、E为凯勒均匀系数、R为堵塞滴头位置分布均匀系数;**和*分别表示在0.01和0.05水平上显著;下同。
Note: Proportion of clogged emitter means percentage of clogged emitters in total; Clogging level means ratio of reduced flux in clogged emitters to designed flux;a,a,a,a′are regression coefficients,b,b,bare constants of regression models, respectively;Cis Christian uniformity coefficient,Eis Keller uniformity coefficient;Ris uniformity coefficient of clogged emitter distribution; ** and * indicate<0.01 and<0.05; Same as follow.
当滴灌系统中堵塞滴头数量较少时,C与各灌水均匀系数线性相关。例如滴头额定流量为0.9 L/h,当堵塞滴头占比约为10%时,3种回归模型的2均保持在0.88以上。当堵塞滴头占比逐渐增多至20%时,C~CR模型的2仍保持为0.994,而C~C与C~E模型的2均减小为0.856,约为C~CR模型的85%。当堵塞滴头占比进一步增加至30%时,C~CR模型的2为0.968,而C~C与C~E模型的2继续减小为0.829。这表明当堵塞滴头数量较少时,堵塞滴头位置分布对土壤水分分布均匀性影响相对较小;当堵塞滴头数量较多时,由于土壤中基质势的影响,水分会在土壤中重新分布,堵塞滴头位置分布状况对土壤水分分布均匀性的影响程度会相应增大。
随着滴头平均堵塞程度逐渐增加,C~CR模型的2保持在0.92以上,而C~C及C~E模型的R则相对较小。由此可知,在本研究设定范围内,无论滴头平均堵塞程度为多少,堵塞滴头位置分布状况均会对土壤水分分布均匀性产生影响。
综上所述,堵塞滴头数量决定了堵塞滴头位置分布对土壤水分分布均匀性的影响程度。当堵塞滴头占比维持在10%以下时,堵塞滴头位置分布对土壤水分分布均匀性影响较小,C、E等评价指标均可较为准确描述土壤水分分布状况;若占比超过10%,仅考虑滴头流量均匀性的评价指标均不能准确反映土壤水分分布状况,应考虑堵塞滴头位置的影响。
2.2.3 考虑堵塞滴头位置分布的优化灌水均匀系数
以文献[26]的研究结果为基础,采用试算法确定考虑滴头堵塞位置的灌水均匀系数中C与R的比例系数,即:
U=k1·C+k2·R(15)
式中U为考虑堵塞滴头位置的优化灌水均匀系数;1、2为U中C、R所占的比例系数,其中121。
将27种堵塞情况下的C与U进行回归分析,参数见表3。

表3 Cuw~UR回归模型的决定系数R2
注:U为考虑滴头堵塞位置分布的优化灌水均匀系数,下同;1、2为U中C、R的比例系数。
Note:Uis optimized uniformity coefficient considering location distribution of clogged emitters, the same below;1and2are monomial coefficients ofCandRinU..
从表3可以看出,当堵塞滴头占比为20%时,U中C和R的最佳比例系数为8:2;堵塞滴头占比为30%时,U中C和R的最佳比例系数为7:3。这与2.3中的结论是一致的,即堵塞滴头位置分布对土壤水分分布均匀性的影响会随堵塞滴头数量增加而增大,但相较于滴头流量而言,其影响仍然较小。
综上,当U中C和R的比例系数为8:2时,U回归模型的2均能保持在一个较高水平,此时U最能反映出滴灌条件下的土壤水分分布状况。其计算公式应为
U=0.8C+0.2R(16)
2.3 优化灌水均匀系数模型的验证
2.3.1 灌水均匀系数与土壤水分分布均匀系数对比分析
根据式(1)、式(2)、式(5)及式(16)计算土壤水分分布及各灌水均匀系数,并将、U与C进行线性拟合。
表4给出了温室验证试验中各堵塞状况下的均匀系数值。当堵塞滴头占比一定时,C不会随堵塞滴头位置的变化而发生改变,但U和C却随着堵塞滴头集中程度的增加而呈现减小的趋势,且变化趋势基本一致。例如当堵塞占比为30%、堵塞滴头较为分散时,C、C和U分别为0.400、0.798和0.434;当堵塞滴头集中分布于毛管尾部时,C仍保持为0.400,C和U却减小为0.759和0.386,这说明U可以反映出由堵塞滴头位置变化而引起的土壤水分均匀性的变化,但整体而言C高于U,即滴灌系统的灌水均匀性低于灌溉水在土壤中的分布均匀性,这与李久生等[30]的研究结果一致。

表4 不同滴头堵塞情况下的均匀系数
2.3.2 优化灌水均匀系数验证分析
通过对比U~C及~C回归模型可以看出,U与C之间的相关性略高(2=0.970)。当堵塞滴头数量较多时,即使出现堵塞滴头全部集中于毛管尾段这种极端情况,C与U之间几乎仍是一一对应关系,而与C之间的差别则较大。说明优化灌水均匀系数能够准确反映灌水小区内的土壤水分状况,故可用来评价滴灌系统灌水均匀性。
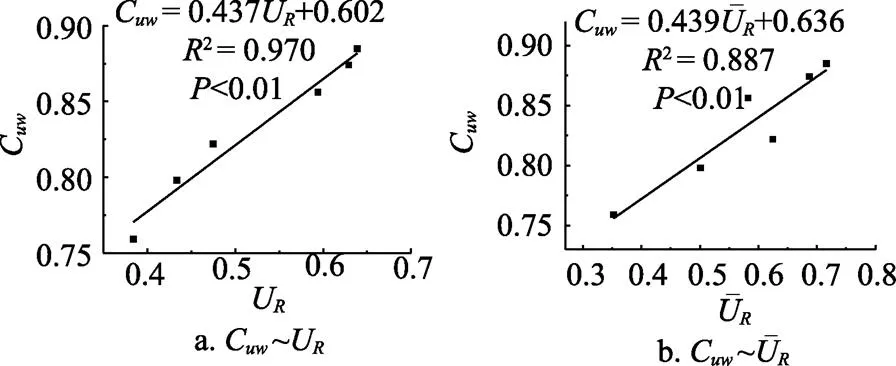
注:ŪR为考虑滴头堵塞位置分布的灌水均匀系数。
3 结论与讨论
1)取样间距和取样深度均对土壤水分分布均匀性有显著影响。适宜的取样间距为60 cm×60 cm,取样深度为20 cm。
2)土壤水分分布均匀系数与滴灌系统灌水均匀系数之间存在良好的线性关系,故可用以评价各灌水均匀系数。
3)滴头堵塞是影响灌水均匀系数的重要因素。若堵塞滴头数量较多(占比>10%),考虑滴头堵塞位置的优化灌水均匀系数能准确反映灌水小区内的土壤水分分布均匀性。
滴灌系统的灌水均匀性及土壤水分分布均匀性是众多因素共同作用的结果,本研究仅考虑了堵塞因素,对于初始土壤含水量、滴头流量等其他因素没有充分考虑。在后续的研究中还需要对其他因素进行逐一分析,明确各因素对土壤水分分布均匀性的影响,为获得适宜的田间土壤水分均匀性提供理论指导。
[1] Christiansen J E. Irrigation by Sprinkling[M]. Berkeley, CA: University of California, 1942.
[2] Criddle W D. Methods for Evaluating Irrigation System[M]. Washington DC: Soil Conservation Service, US Dept of Agriculture, 1956.
[3] Beale J G. Distribution Uniformity of Sprinkler Irrigation Systems[M]. Kensington: University of New South Wales, 1965.
[4] Keller J, Karmeli D. Trickle irrigation design parameters[J]. Transactions of the ASAE, 1974, 17(4): 678-684.
[5] Nakayama F S, Bucks D A. Assessing trickle emitter application uniformity[J]. Transactions of the ASAE, 1979, 22(4): 816-821.
[6] Solomon K. Manufacturing variation of trickle emitters[J]. Transactions of the ASAE. 1979, 22 (5): 1034-1038.
[7] Bralts V F, Wu I P, Gitlin H M. Drip irrigation uniformity considering emitter plugging[J]. Transactions of the ASAE, 1981, 24(5): 1234-1240.
[8] Bralts V F, Kesner C D. Drip irrigation field uniformity estimation[J]. Transactions of the ASAE, 1983, 22(3): 1369-1374.
[9] Keller J, Bliesner R D. Sprinkler and Trickle Irrigation[M]. New York: van Nostrand Reinhold, 1990.
[10] Barragan J, Bralts V F, Wu I P. Assessment of emission uniformity for micro-irrigation Design[J]. Biosystems Engineering, 2006, 93(1): 89-97.
[11] Wu I P, Gitlin H M. Design of Drip Irrigation Lines[D]. Honolulu: University of Hawaii, 1974.
[12] Bralts V F, Wu I P, Gitlin H M. Manufacturing variation and drip irrigation uniformity[J]. Transactions of the ASAE, 1981, 24 (1): 113-119.
[13] Howell T A, Hilter E A. Trickle irrigation lateral design[J]. Transactions of the ASAE, 1974, 17(5): 902-908.
[14] 郑耀泉,宁堆虎. 滴头制造偏差的模拟与滴灌系统随机设计方法的研究[J]. 水利学报,1991(7):1-7. Zheng Yaoquan, Ning Duihu. Simulation of emitter manufacturing deviation and development of stochastic design method for trickle irrigation system[J]. Journal of Hydraulic Engineering, 1991(7): 1-7. (in Chinese with English Abstract)
[15] 郑耀泉,陈渠昌. 微灌均匀度参数之间的关系及其应用[J]. 灌溉排水,1994,13(2): 7-10.Zheng Yaoquan, Chen Quchang. The relation among uniformity parameters of micro-irrigation and their use[J]. Irrigation and Drainage, 1994, 13(2): 7-10. (in Chinese with English Abstract)
[16] 张国祥. 考虑三偏差因素的滴灌系统流量总偏差率[J]. 农业工程学报,2006,22(11):27-29. Zhang Guoxiang. Calculating the total flow deviation rate of drip-irrigation system based on three deviation rates[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2006, 22(11): 27-29. (in Chinese with English Abstract)
[17] 张国祥. 用凯勒均匀度进行微灌系统设计的质疑[J]. 农业工程学报,2008,24(8):6-9. Zhang Guoxiang. Query about micro-irrigation system design using Keller Uniformity[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(8): 6-9. (in Chinese with English Abstract)
[18] 牛文全,吴普特,范兴科. 微灌系统综合流量偏差率的计算方法[J]. 农业工程学报,2004,20(6):85-88. Niu Wenquan, Wu Pute,Fan Xingke. Method for calculating integrated flux deviation rate of micro-irrigation system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2004, 20(6): 85-88. (in Chinese with English Abstract)
[19] 张林,范兴科,吴普特,等. 均匀坡度下考虑三偏差的滴灌系统流量偏差率的计算[J]. 农业工程报,2009,25(4):7-14. Zhang Lin, Fan Xingke,Wu Pute, et al. Calculation of flow deviation rate of drip irrigation system taking three deviation rates into account on uniform slopes[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(4): 7-14 (in Chinese with English Abstract)
[20] 张林,吴普特,牛文全,等. 均匀坡度下滴灌系统流量偏差率的计算方法[J]. 农业工程学报,2007,23(8):40-44. Zhang Lin, Wu Pute, Niu Wenquan, et al. Method for calculating flow deviation in drip irrigation system under uniform slope[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2007, 23(8): 40-44. (in Chinese with English Abstract)
[21] 张林,吴普特,朱德兰,等. 基于制造偏差的滴灌系统综合流量偏差率[J]. 农业机械学报,2013,44(12):135-139. Zhang Lin, Wu Pute, Zhu Delan, et al. Integrated flow deviation rate of drip irrigation system based on manufacturing variation [J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(12): 135-139. (in Chinese with English Abstract)
[22] 朱德兰,吴普特,张青峰,等. 微地形影响下滴灌均匀度设计指标研究[J]. 排灌机械,2006,24(1):22-26. Zhu Delan, Wu Pute, Zhang Qingfeng, et al. Study on the emission uniformity for the emitter under the condition of farmland micro-terrain action[J]. Drainage and Irrigation Machinery, 2006, 24(1): 22-26. (in Chinese with English Abstract)
[23] 朱德兰,吴普特,王剑. 滴头制造偏差对灌水均匀度及毛管造价的影响[J]. 排灌机械工程学报,2011,29(2):175-179. Zhu Delan, Wu Pute, Wang Jian. Effect of emitters manufacturing variation of micro-irrigation on uniformity and lateral cost[J]. Journal of Drainage and Irrigation Machinery Engineering, 2011, 29(2): 175-179. (in Chinese with English Abstract)
[24] Zhu D L, Wu P T, Merkley G P. Drip irrigation lateral design procedure based on emission uniformity and field microtopography[J]. Irrigation and Drainage, 2010, 59(5): 535-546.
[25] Capra A, Scicolone B. Water quality and distribution uniformity un drip/trickle irrigation systems[J]. J Agric Eng Res, 1998, 70(4): 355-365.
[26] 牛文全,张若婵,罗春艳. 考虑滴头堵塞位置分布的灌水均匀度计算方法[J]. 农业机械学报,2015,46(6):147-152,174. Niu Wenquan, Zhang Ruochan, Luo Chunyan. Drip irrigation uniformity calculation considering distribution location of clogged emitters[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(6): 147-152, 174. (in Chinese with English Abstract)
[27]宰松梅,仵峰,温季,等. 大田地下滴灌土壤水分分布均匀度评价方法[J]. 农业工程学报,2009,25(12):51-57. Zai Songmei, Wu Feng, Wen Ji, et al. Evaluation method of soil water distribution uniformity under conditions of field subsurface drip irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(12): 51-57. (in Chinese with English Abstract)
[28] 张林,吴普特,范兴科. 多点源滴灌条件下土壤水分运动的数值模拟[J]. 农业工程学报,2010,26(9):40-45. Zhang Lin, Wu Pute, Fan Xingke. Numerical simulation of soil water movement with drip irrigation of multiple point source[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(9): 40-
45. (in Chinese with English Abstract)
[29] 李久生,张建君,饶敏杰. 滴灌施肥灌溉的水氮运移数学模拟及试验验证[J]. 水利学报,2005,36(8):932-938. Li Jiusheng, Zhang Jianjun, Rao Minjie. Model verification of water and nitrate transport from a surface point source[J]. Journal of Hydraulic Engineering, 2005, 36(8): 932-938. (In Chinese with English abstract)
[30] 李久生,饶敏杰. 喷灌均匀系数对土壤水分及冬小麦产量影响的试验研究[J]. 水利学报,2000(1):9-14. Li Jiusheng, Rao Minjie. Effects of sprinkler uniformity on spatial variability of soil moisture and winter wheat yield[J]. Journal of Hydraulic Engineering, 2000(1): 9-14. (in Chinese with English Abstract)
Optimization of drip irrigation uniformity model considering location of clogged emitters
Zhang Ruochan1, Niu Wenquan1,2,3※, Duan Xiaohui3, Li Yuan3
(1.712100,;2.712100,;3.712100,)
Uniformity is one of the most important indicators for the evaluation of drip irrigation quality, and is also regarded as an important parameter for drip irrigation system design. Soil water distribution uniformity is the ultimate expression of drip irrigation uniformity, but the present drip irrigation uniformity indexes can’t reflect it directly. In this study, we used soil water distribution coefficient as the standard to evaluate the rationality and accuracy of 3 typical drip irrigation uniformity coefficients (Christiansen uniformity coefficient, Keller uniformity coefficient and the uniformity coefficients considering location of clogged emitters) and finally optimized the best one among these 3 coefficients. Three factors (clogged degree, proportion of clogged emitter, location of clogged emitters) influencing the drip irrigation uniformity were considered, and a total of 27 kinds of drip irrigation situations (clogged degree of 40%, 60% and 80%; proportion of clogged emitter of 20%, 30% and 40%; location of clogged emitters of even distribution, relative uniform and nonuniform distribution) were designed. The soil water distribution of each irrigation situation was simulated by HYDRUS-2D program and verified by an actual infiltration experiment. We matched soil water distribution coefficient and the irrigation uniformity coefficients of each irrigation situation, then compared and evaluated them by linear fitting. Soil water distribution coefficient was significantly influenced by sampling arrangement, therefore 9 kinds of sampling arrangements were set up and a desirable one was chosen through variance analysis. Results showed that under the condition of the simulation test, the desirable sampling interval and depth were 60 and 20 cm respectively for soil moisture monitoring. Based on the desirable sampling arrangement, there was a significant linear relevance between soil water distribution uniformity and irrigation uniformity. Among them, the uniformity coefficient considering location of clogged emitters could reflect the soil water distribution accurately; it had the optimal linear relationship with soil water distribution coefficient. According to this linear relationship,the uniformity coefficient considering location of clogged emitters could be optimized when the regression coefficient ratio for the content of clogged emitters’ location uniformity and the Christiansen uniformity coefficient was 2:8. A field experiment was done in a solar heated greenhouse in order to verify the accuracy of the optimized uniformity coefficient considering location of clogged emitters. The field experiment result was consistent with the simulation result, both of which showed a significant linear relationship between soil water distribution coefficient and the optimized uniformity coefficient considering location of clogged emitters. With the increase of clogged emitters, the influence of clogged emitters’ location on soil water distribution uniformity would also increase. If the clogged emitter accounted for a large proportion (>10%), the relationship between soil water distribution coefficient and the optimized uniformity coefficient considering location of clogged emitterswas closer than it between soil water distribution coefficient and the other uniformity coefficients (2=0.970,<0.01). Therefore, the optimized uniformity coefficient considering location of clogged emitters was more proper when evaluating the irrigation uniformity. Its evaluation result was consistent with the soil moisture situation and could reflect the actual irrigation quality comprehensively. But in general, soil water distribution coefficientwas higher than the optimized uniformity coefficient considering location of clogged emitters, indicating that the soil moisture was more uniform because of the soil matrix suction and the redistribution of soil water.
soil moisture; irrigation; optimization; emitter clogging; irrigation uniformity; soil water distribution uniformity; clogging location
10.11975/j.issn.1002-6819.2017.03.015
S275.4
A
1002-6819(2017)-03-0113-08
2016-08-12
2016-09-21
“十二五”国家科技支撑计划资助项目(2015BAD24B01)
张若婵,女,陕西杨凌人,主要从事节水灌溉技术研究。杨凌西北农林科技大学水利与建筑工程学院,712100。 Email:zrc1991@nwsuaf.edu.cn
牛文全,男,甘肃天水人,研究员,博士生导师,主要从事水土资源高效利用与节水灌溉技术研究。杨凌中国科学院水利部水土保持研究所,712100。Email:nwq@vip.sina.com
张若婵,牛文全,段晓辉,李 元. 考虑滴头堵塞位置的灌水均匀系数模型优化[J]. 农业工程学报,2017,33(3):113-120. doi:10.11975/j.issn.1002-6819.2017.03.015 http://www.tcsae.org
Zhang Ruochan, Niu Wenquan, Duan Xiaohui, Li Yuan. Optimization of drip irrigation uniformity model considering location of clogged emitters[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(3): 113-120. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2017.03.015 http://www.tcsae.org
