论单圈图的特征值上界
2017-03-03马志辉
马志辉
(石河子大学 理学院,新疆 石河子 832000)
论单圈图的特征值上界
马志辉
(石河子大学 理学院,新疆 石河子 832000)
以图的谱来刻划图的结构性质是图的谱理论中重要的研究问题之一.一方面图谱在量子化学、信息科学等学科中均有一系列的重要应用.另一方面图谱理论发展的同时也促进和丰富了图论和组合数学本身的研究,谱技巧已经成为图论和组合数学研究中一个重要的工具.本文证明了阶连通单圈图的第个特征值的上界
单圈图;上界;特征值
1 引言
本文所研究的单圈图是恰含一个圈的简单连通图,单圈图G的特征值就是它的邻接矩阵A(G)的特征值,A(G)的特征,多项式记为P(G,λ),如果G是一个n阶单圈图,则A (G)是一个n阶对称(0,1)矩阵,故A(G)的第n个特征值,也就是G的第n个特征值全为实数,我们可以按递降次序将它们排列为:

称λk(G)为G的第k个特征值.
在没有特别说明的情况下,本文的G均代表n阶连通的单圈图.
洪渊证明了:
1:λ1(G)≤λ1(S2n),当n≥9的时候,有,其中Sn2是连接星图Ktn-1的两个一度点而得到的图.
2.λ1(G)=λ1(S2n)GSn2其中表示同构.
邵嘉裕研究了n阶树T的特征值的上界,所得结果如下:
对全部n≠0(modk)时,上界是最好可能上界.
2.当n=0(modk),上界(1)中严格不等式成立,但是对于任意ε>0,一般不成立.
3.当n=0(modk),存在n阶树T*,使得:

本文在上述研究基础上,对n阶连通单圈图G的第个特征值的上界问题证明了:
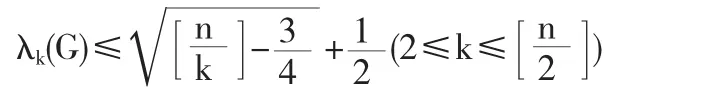
2 引理
引理1 柯西插入定理
设V是G的一个含个点的点子集,G-V表示G删除V中点以及和V中点相关联的所有边后所得的子图,则有:
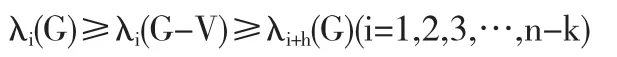
证 设θ是G的非孤立点,以θ为根长出的所有l+1个顶点的数Tl+1所得的图集,记为GT(θ,1),当Tl+1为星图Kl+1,记所的图为
引理2 对任一Gl∈GT(θ,1),Gl与不同构,有:
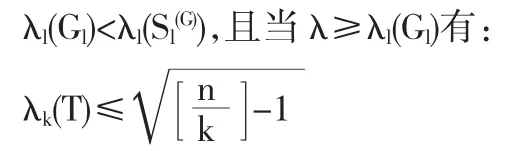
引理3 如果T为任一n阶树,那么对于任何一个正整数k,2≤k≤,存在V∈V(T),使得|V'|=k-1,且T-V全部分支阶树都不超过
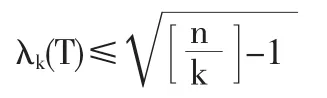

证 不妨设G是n阶树T添加一边e=[μ,θ]而形成的,即G=T+e
由引理3可知,存在V∈(V(T)=V(G),使|V'|=k-1,且T-V的所有分支的阶数不超过,令T-V的所有分支为T1,T2,…,Ti,下面就e所在位置几种情形讨论.
情形1:μ∈V或θ∈V,则,T1,T2,…,Ti,就G-V的所有分支.从而(2.1)成立.
情形2:e在某分支T1中,则T1为单圈图,[V(Ti)]≤,令T1=Ti,于是条件成立.
情形3:e作为割边连接了T的某两个分支,不妨设为T1,T2,令Ti=T1UT2U[e]则有
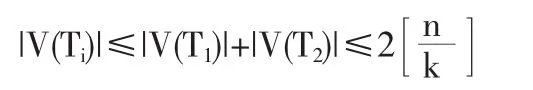
于是条件(3.3)成立,故,引理得证.
3 结果
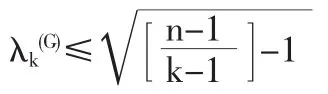
证任意圈上的某点θ,记G'=G-θ,则G为n-1阶森林.因此有:λk(G)≤λk-1(G')(引理1)
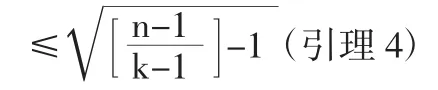
证毕.

图1 Gt
易得:P(Gt,λ)=λ2t-4(λ4-(2t-1)λ2+(t-1)2)

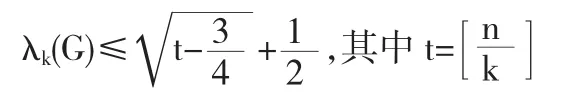
证由引理5可知,存在V⊆V(G),|V|=k-1,使G-V的所有分支T1,T2,…,Tm满足(2.1),(2.2),(2.3)之一,下面分几种情形讨论.


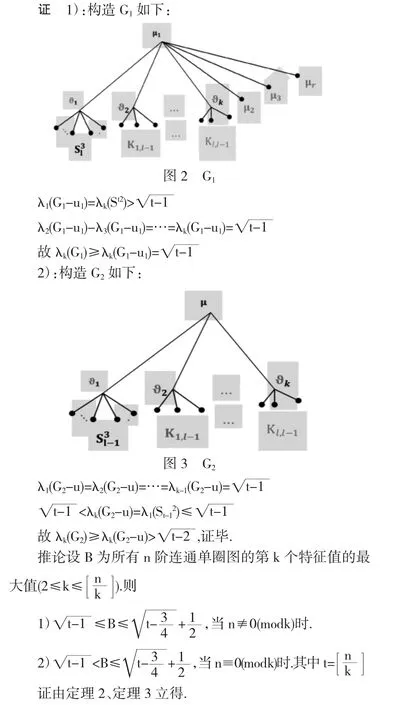
1)当n≡0(modk),且t≥1时,存在n阶单圈图G1,使λk
2)当n≡0(modk),且t≥2时,存在n阶单圈图G2,使λk
〔1〕于广龙.有关组合矩阵论中图谱与符号模式矩阵的研究[D].华东师范大学,2011.
〔2〕田路路.简单连通图的邻接谱半径的若干问题的研究[D].华侨大学,2013.
〔3〕李国君.关于图的零度和无符号拉普拉斯谱半径的研究[D].北京交通大学,2014.
〔4〕扈生彪.单圈图的最大特征值的上界的改进(英文)[J].数学研究与评论,2009(05):945-950.
O157.5
A
1673-260X(2017)01-0001-02
2016-10-10
石河子大学高层次人才科研启动资金专项(RCZX201418);石河子大学应用基础研究青年项目(2015ZRKXYQLH09)
