无感蔡氏电路混沌同步控制实验
2017-03-02闵富红彭光娅叶彪明王恩荣
闵富红, 彭光娅, 叶彪明, 王恩荣
(南京师范大学 电气与自动化工程学院, 江苏 南京 210042)
无感蔡氏电路混沌同步控制实验
闵富红, 彭光娅, 叶彪明, 王恩荣
(南京师范大学 电气与自动化工程学院, 江苏 南京 210042)
设计了综合性强的非线性电路实验,基于合适的线性反馈控制器,实现运动行为不同的2个蔡氏电路系统的混沌同步控制。利用非线性限幅函数,设计等效无感蔡氏电路的同步控制电路图,电路结构简单易操作。通过调节电位器的阻值,改变同步控制器的增益,观测实验结果,驱动系统与响应系统达到渐近同步。通过非线性电路系统的开发式实验,培养了学生的创新能力和科研能力,有利于非线性电路课程的深入学习和理解。
电路实验; 蔡氏电路; 同步控制
蔡氏电路是非线性电路中产生复杂动力学行为的最简单的混沌振荡电路之一,由美国加州大学蔡少棠教授[1-5]于1983年提出。蔡氏电路作为一种典型的非线性电路,其结构简单,易于电路实验和改建,运动行为丰富,可广泛应用于非线性科学和保密通信等领域。因而,蔡氏电路的混沌同步控制已经成为当前非线性科学中的一个热点课题。文献[6]使用Multisim仿真软件研究了电路元件参数对称和不对称情况下蔡氏电路的混沌控制与同步;文献[7]针对经典三阶蔡氏电路,提出一种利用符号函数的非线性投影同步控制方法,并完成了硬件电路实验;文献[8]基于稳定性理论,数值模拟了变形蔡氏电路的同步和错位同步的问题;文献[9]提出了一种绝对值函数反馈控制的同步法,实现了变形蔡氏电路的函数同步控制的软件仿真和硬件电路实验;文献[10]基于T-S模糊法实现了蔡氏电路的输出反馈同步;文献[11]设计了分数阶蔡氏电路同步控制的无感模块化电路图并完成了模拟实验。以上工作为蔡氏电路同步的研究奠定了良好的基础,但有些控制方法过于理论化,没有实际硬件电路实验。另外,由于传统蔡氏电路电感元件的存在,在进行硬件电路实验调试时,误差较大且设计精度很难满足要求。为此,本课题组根据蔡氏电路系统中变量的运算关系,利用运算放大器的限幅原理[12],设计了等效的无感蔡氏电路[13],通过实验演示发现其输出的周期运动、混沌吸引子与经典蔡氏电路的运动行为完全相同,且硬件电路实验易于调试。
本文提出基于模块化的等效无感蔡氏电路系统,设计简单的反馈控制器,实现运动行为不同的蔡氏电路系统混沌同步控制实验。通过改变电位器的阻值,调节同步控制器的增益,使得驱动系统与响应系统渐近同步,以加深学生对非线性电路的认知。通过对蔡氏电路同步控制的电路设计、软件模拟仿真、硬件电路调试以及观测分析实验结果,提高学生的电路设计能力和实践能力,培养了学生创新思维的能力。
1 问题描述
蔡氏电路系统已被广泛用于高校的物理学和电路课程的实验教学中。蔡氏电路无量纲的数学模型为:
(1)
为了观测具有不同运动行为的2个蔡氏电路系统同步,设式(1)系统为驱动系统,则受控的响应系统为:
(2)
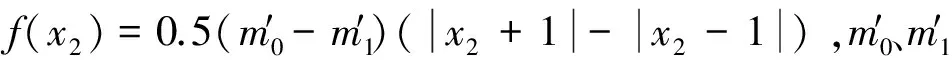
u=(u1,u2,u3)T为要设计的同步控制函数。
根据设计的不同控制器u,可使得驱动系统与响应系统的输出达到完全同步、投影同步或者函数同步等。在进行非线性电路实验过程中,学生可以自由选择不同的控制器进行电路设计,观测同步关系,从而提高学生的创新能力。由于蔡氏电路的系统状态变量z由y直接控制,因此控制了变量y以后无需对z再进行同步控制。因而提出一种基于3个状态变量添加控制环节、实现2个状态变量同步控制的方法,实现2个运动行为不同的蔡氏电路同步,设计的合适线性反馈控制器为:
(3)
其中,参数k1、k2为控制增益,p1、p2为比例系数。当p1=p2=1时,则实现2个混沌系统的完全同步,否则属于投影同步。所设计的同步控制方法简单,便于观测得到实验结果。
2 蔡氏系统同步电路的设计
在经典蔡氏电路系统中,包括1个电感、1个电阻、2个电容以及一个非线性电阻环节。其中,非线性电阻环节是系统产生混沌运动的关键。由于混沌的初始敏感性,在实际电路实验中对电感的精度要求很高,从而很难观测到稳定的混沌运动。为此,课题组利用运算放大器的限幅特性,实现非线性的不连续特性,设计了只包含电阻、电容、运算放大器及二极管等元器件的无感等效蔡氏电路,通过调节阻容元件的大小,很容易从示波器中观测不同的周期运动与混沌吸引子的时序图、李莎育图形。基于等效的无感蔡氏电路图,设计的驱动系统、响应系统及控制器的模块化同步控制电路图见图1。图1中虚框部分为同步控制器电路,是由运算放大器和电阻构成的减法电路。根据电路的基本理论以及各个元件的特征,得到驱动系统的电路状态方程如下:
(4)
非线性函数电路由电阻R1、R2、R3,以及2个导通电压约为0.65V的1N5712型二极管以及正负电源共同实现,具体表达式为:
(5)
比较式(1)与式(4)得到驱动系统各参数的表达式为:
(6)
同样道理,受控的响应系统(见式(2))的电路表达式为:
(7)

图1 同步控制系统电路图
其中,非线性环节选择元件与驱动系统部分一致,表达式为:
(8)
并且控制器部分的表达式为:
(9)
将受控的响应系统(见式(2))、控制器(见式(3))与式(7)比较,则系统参数的表达式为:
(10)
若取电阻Ra1=Ra2=Ra3=Ra4=10 kΩ,Rb1=Rb2=Rb3=Rb4=10 kΩ时,由图1可得可知控制器部分的控制增益与比例因子分别为:
(11)
比例因子p1、p2的值定为1,表示驱动系统与响应系统状态变量的达到完全同步,当然根据实际需要通过调节相关电阻,p1、p2的值也可以进行调节,以实现不同的同步控制类型。如果固定电容C1的值,只要调节电位器Ra5和Rb5的值,就可以改变同步控制器增益的大小,实现驱动系统与响应系统的同步控制。
3 硬件电路实验
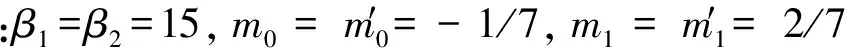
在实验过程中,使用UTD4062C型号的示波器观察整个系统的运行情况。首先调节电位器,分别观测未施加控制器之前驱动系统与响应系统的运动。当选取α1=9.5时,阻值R4=35 kΩ、R5=3.5 kΩ、R8=1 kΩ,驱动系统运动状态为多涡卷吸引子,如图3(a)所示;当选取α2=9.0时,阻值R18=38.89 kΩ、R19=3.89 kΩ,R22=1.11 kΩ,此时响应系统处于单涡卷混沌吸引子,如图3(b)所示。然后,合上控制开关,调节电位器Ra5和Rb5的阻值,当Ra5=Rb5=100 Ω,即k1=k2=100时,观测到驱动系统与响应系统达到完成同步,响应系统由单涡卷吸引子迅速转换为双涡卷混沌运动,如图4所示。可见,驱动-响应系统:x1-x2、y1-y2和z1-z2曲线拟合是斜率为1的直线,驱动系统与响应系统的全状态变量的时序图都渐近同步,充分地验证这种新型控制器的可行性。
与经典蔡氏电路系统的同步控制电路相比较,这里硬件实验中使用了等效的无感蔡氏电路,电路结构简单,易于调试,可以从示波器直接观测中3个系统状态变量的同步情况,波形稳定,实验效果好。该实验激发了学生对非线性电路的深入学习的兴趣。
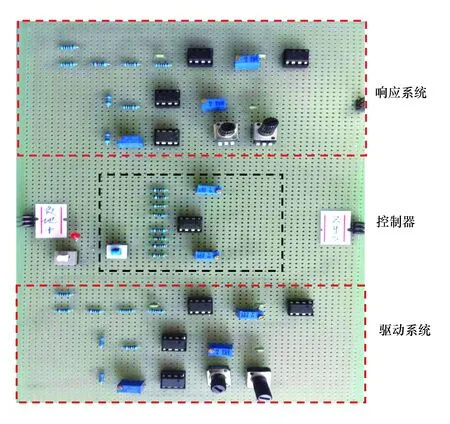
图2 同步控制系统电路实物图
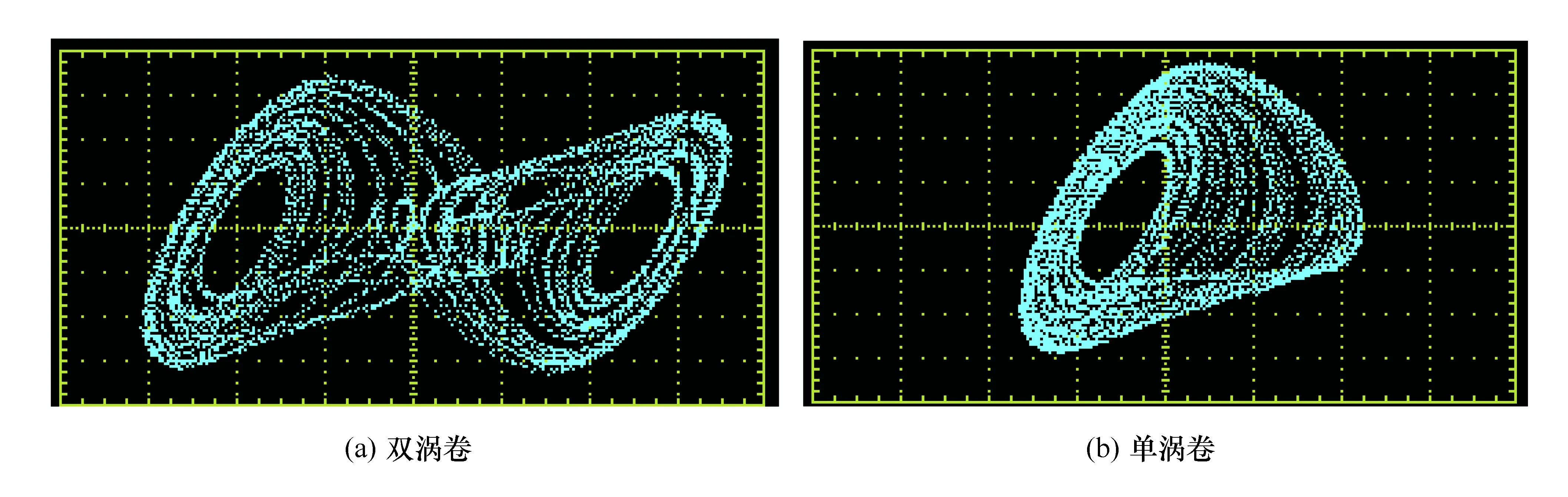
图3 未加控制前驱动系统与响应系统的x-y相图

图4 同步控制效果图
4 结论
本文以经典蔡氏电路为研究对象,基于简单的反馈控制方法实现了具有不同运动的2个混沌系统同步,设计了等效无感蔡氏电路的同步控制电路图,焊接电路板,完成了硬件实验的测试,实现了全状态变量的完全同步。实验结果符合设计要求,电路简单易懂,可操作性强。通过完成无感蔡氏电路同步的实验,调节电位器可以观测到系统的周期运动与混沌吸引子,加深了学生对非线性电路的认识,让学生熟悉了混沌同步控制。此外,学生可利用Multisim软件完成电路模拟仿真,并将仿真结果与硬件电路实验测试结果比较,进一步验证该方法的可行性与有效性。当然,学生还可以继续实现实验内容的创新,设计不同的控制器电路,完成相应的软硬件实验,观测不同实验结果,从而拓宽眼界,提高其科研创新能力。
)
[1] 禹思敏. 混沌系统与混沌电路:原理、设计及其在通信中的应用[M]. 西安:西安电子科技大学出版社,2011.
[2] 谢永兴,胡云安,林涛,等. 蔡氏混沌电路联合仿真方法研究[J]. 仪表技术,2016,45(1):11-14.
[3] 鲍林云,周尚波,虞继敏,等. 蔡氏电路的混沌仿真研究[J].山东工业技术,2015,35(1):254-256.
[4] 杜宇上,肖化. 基于Multisim的混沌电路仿真实验[J]. 实验室研究与探索,2013,32 (1):42-45.
[5] 代琼琳,吴昊,王亚苗. 非对称电压对蔡氏电路混沌现象影响的研究[J]. 实验技术与管理,2009, 26(6):39-41.
[6] 钟双英,刘崧,戚小平,等. 蔡氏电路混沌控制与同步实验研究[J]. 实验技术与管理,2012,29(11):32-34.
[7] 马美玲,闵富红,邵书义,等. 基于符号函数的注入反馈式蔡氏电路同步控制[J]. 物理学报,2014,63(3):1-7.
[8] 刘颖,王瑞琦,吴红梅,等. 变形蔡氏电路混沌系统的同步与错位同步[J].连云港职业技术学院学报,2011,24(1):1-4.
[9] 黄苗玉,闵富红,王恩荣,等. 采用绝对值反馈的混沌系统投影同步的电路实现[J]. 华侨大学学报(自然科学版),2015,36(4):437-442.
[10] 施伟丰,蒋国平. 基于T-S模糊模型的蔡氏混沌电路及其输出反馈同步[J]. 南京邮电大学学报(自然科学版),2016,36(3):121-127.
[11] 邵书义,闵富红,马美玲,等. 分数阶Chua’s系统错位同步无感模块化电路实现及应用[J]. 物理学报,2013,62(13):130514-1-130514-08.
[12] 张新国,许崇芳,王金双,等. 无电感蔡氏电路设计方法与应用[J]. 山东大学学报,2010,40(6):134-138.
[13] 闵富红,马美玲. 基于二极管的限幅蔡氏电路实验研究[J]. 电气电子教学学报,2014,36(4):48-51.
Experiment on chaotic synchronous control of Chua’s circuit without inductors
Min Fuhong, Peng Guangya, Ye Biaoming, Wang Enrong
(School of Electrical and Automation Engineering,Nanjing Normal University,Nanjing 210042,China)
A strong comprehensive nonlinear circuit experiment is designed, and based on linear feedback controller, the chaotic synchronization control for two Chua’s circuits with different motion is realized. By using the nonlinear limiting amplitude function, the synchronous control circuit diagram of Chua’s circuit without inductors is designed. Its circuit structure is simple, and its operation is easy. Through adjusting the resistance value of the potentiometer, the gain of the synchronous controller is changed. In the observation of the experimental results, the asymptotic synchronization is achieved for the drive system and response system. Through the open experiment of nonlinear circuit, the students’ innovative ability and scientific research ability are cultivated, and it is also helpful for the students to gain the deep learning and understanding of Nonlinear Circuit course.
circuit experiment; Chua’s circuit; synchronous control
10.16791/j.cnki.sjg.2017.02.012
2016-08-08 修改日期:2016-10-09
国家自然科学基金项目(51475246); 江苏省自然科学基金项目(BK20131402);江苏省研究生教育教学改革研究与实践项目(JGLX16_016); 南京师范大学研究生教育教学改革研究与实践重点课题
闵富红(1970—),女,江苏海安,博士,副教授,研究方向为非线性电路的教学与研究.
E-mail:minfuhong@njnu.edu.cn
G642.3, TM132
A
1002-4956(2017)2-0043-04
