基于线性化数据处理的位置指纹算法

丁绪星，王兵兵

(安徽师范大学 物理与电子信息学院,安徽 芜湖 241000)

基于线性化数据处理的位置指纹算法

丁绪星，王兵兵

(安徽师范大学 物理与电子信息学院,安徽 芜湖 241000)

为了进一步提高室内定位精度，提出了一种改进的位置指纹定位算法。该算法离线阶段采集采样点信号强度构建数据库，在线阶段采用线性拟合和最小二乘法相结合求出待测点的估计位置。仿真结果表明，改进的算法尤其适用于不大于10 m*10 m的小区域网络的高精度定位，与传统的位置指纹算法相比较，改进的位置指纹定位算法使得平均定位误差降低了22.2%，提高了定位精度。

位置指纹算法；线性拟合；最小二乘法；高精度

0 引言

随着移动通信和无线网络的发展，位置服务已经在大型停车场、物品查找、医疗和商场等大众公共服务领域得到越来越多的应用[1-3]，其中，定位的精度是决定位置服务质量的关键。目前，室内定位应用较多的算法是位置指纹定位算法。

位置指纹是根据接收的信号强度[4-5]矢量与定位位置存在一一对应关系，而进行的位置估计。位置指纹定位算法根据数据库信号指纹表示的不同可分为2类：① 基于概率的定位方法，该方法通过条件概率为位置指纹建立模型，采用贝叶斯方法来估计待测点的位置[6]；② 确定性定位算法，该方法常见的算法有最近邻法、KNN算法及WKNN算法等。针对传统位置指纹定位算法定位精度不够，近年来,很对学者们提出很多不同的改进算法。文献[7]提出了EKNN算法，该算法提高了定位精度，但运算量较大。文献[8]基于能效的WLAN室内定位系统模型设计与实现采用分步定位：粗定位和精定位，在一定程度上减小了计算量，提高了定位精度。文献[9]提出了指数加权KNN算法，对定位精度有一定程度的提高。文献[10]提出采用位置指纹与粒子群和克里金(Kriging)空间插值算法相结合的方法，其减小了定位误差，但算法比较复杂。针对位置指纹定位精确度有待提高，或者定位精度高但是算法复杂，提出了在位置指纹定位算法的在线阶段采用线性化拟合的方法来进行数据处理，然后改用最大似然估计算法思想对待测点进行位置估计，并与最大似然估计和加权KNN算法比较，仿真结果证明，在小区域范围定位中，改进的算法进一步提高了定位精度。

1 位置指纹定位算法

1.1 位置指纹算法

位置指纹[11-12]定位是采用RSSI信号强度，进行特征匹配的算法。其算法分为2个阶段：离线阶段和在线阶段。

离线阶段：该阶段主要确定参考点和各个采样点的信号强度与位置来构建指纹数据库。数据库如表1所示。

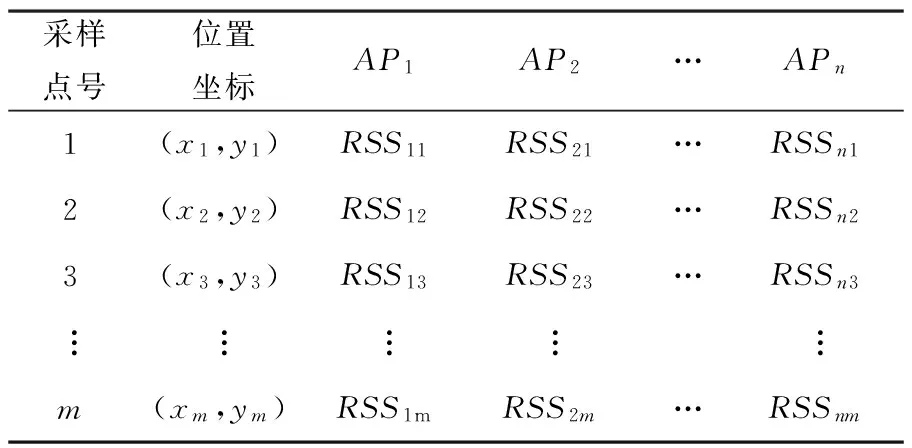
表1 位置指纹数据库

在线阶段：该阶段通过采集待测点的信号强度值，利用欧式距离匹配算法与指纹数据库中的数据进行比较、匹配，从而找到最佳相似点，最后得到待测点的位置估计。其中，待测点的信号强度为(RSS1,RSS2,…,RSSn)，则与第i个的采样点的欧氏距离如下所示：

(1)

1.2 改进算法采用的信号传播模型

在本文仿真中，选用的是室内对数损耗传播模型[13-14]，该模型综合考虑室内的复杂环境，能比较精确地反应无线信号在室内的传播损耗，公式如下：

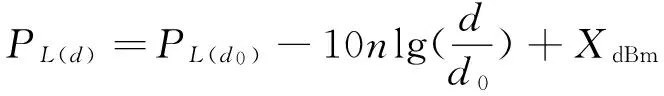
(2)

式中，PL(d)为接收信号强度，PL(d0)为d0m处接收信号强度，n为路径损耗系数，XdBm为噪声误差。

1.3 改进算法的算法过程

首先，对于距离比较近的2点，其信号强度与距离之间可以看成线性关系。对于位置指纹定位在线阶段，找到k个相似点，假定k= 2，则这2个点接收到各个AP点的信号强度分别为(RSS1i,RSS2i,…,RSSni)和(RSS1j,RSS2j,…,RSSnj)，这2个点的位置分别为(xi,yi)和(xj,yj)。待测点测得的信号强度为(RSS1,RSS2,…,RSSn)，其位置为(x,y)。因为待测点和这2个相似点的距离较近，它们的信号强度变化与距离变化近似成线性关系。可以由相似点的信号强度和到AP点的距离建立一个线性方程，之后把待测点的信号强度带入方程得到待测点到AP点的距离。例如：如果相似点到AP1的距离已知为分别为d1i和d1j，因为其接受到AP1的信号强度分别为RSS1i和RSS1j，从而得出线性方程为：

(3)

其次，将待测点对于AP1的信号强度RSS1带入式(3)中，得到该待测点到AP1的距离d1，同理可以得出待测点到其他各个AP点的距离，假定分别为d2、d3、…、dn。每一个锚节点AP的位置点已知，分别为(xAP1,yAP1)、(xAP2,yAP2)、…、(xAPn,yAPn),由此可以得出如下方程组：

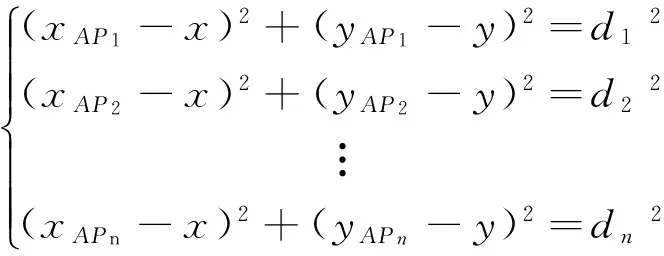
(4)

因为上面方程组为非线性方程组，不易求解。将式(4)线性化处理后，其转化求下面方程组：

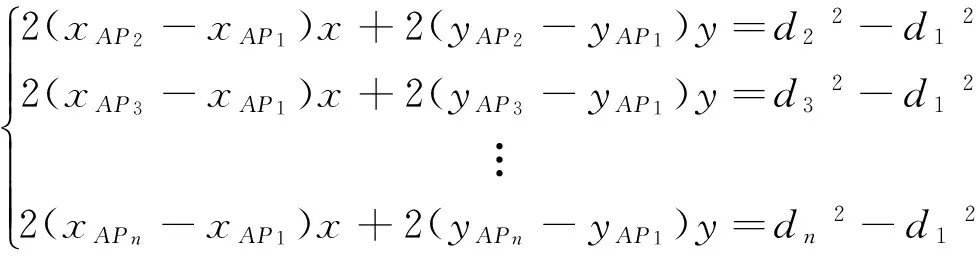
(5)

考虑到误差的存在，因为方程组不一定有解，将上面方程组的每个方程右侧加上一个误差，使得方程组有解，改后的方程如下所示：

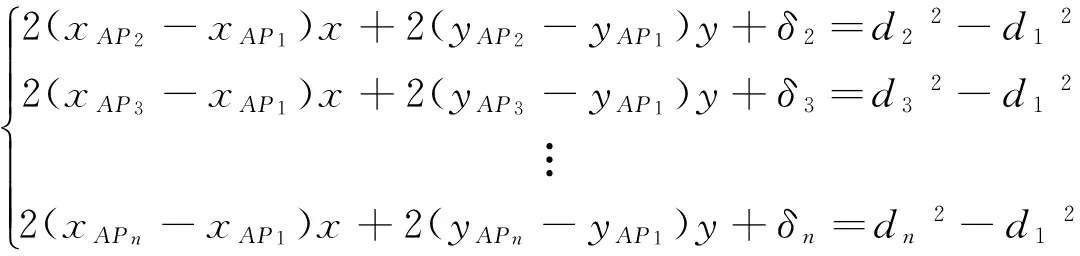
(6)

令：

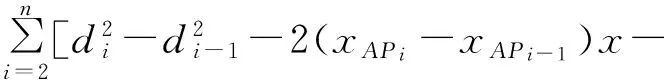
(7)

得：

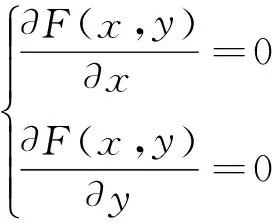
(8)

最后,最小二乘法使δ22+δ32+…+δn2的结果最小，由式(8)解出x、y的值，即可得出待测点的估计位置。

2 仿真实验

采用无线传感网络仿真平台Atos—SensorSim对本文算法进行仿真，同时与最大似然估计算法和加权KNN算法进行了仿真对比。在10m*10m环境中设置100个采样节点，节点间间隔1m，如图1所示。同时，在该区域的边缘设置4个锚节点(标号AP1、AP2、AP3和AP4)，区域内设置6个待测点(标号TP1、TP2、TP3、TP4、TP5和TP6)，分布如图2所示。

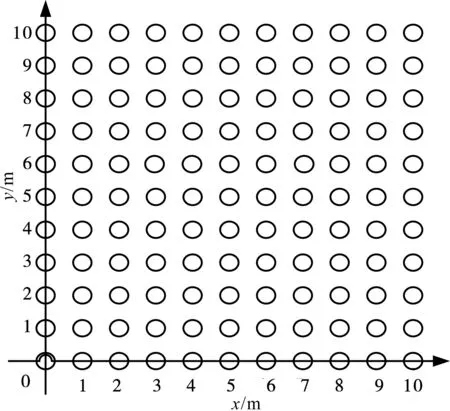
图1 离线阶段采样点位置

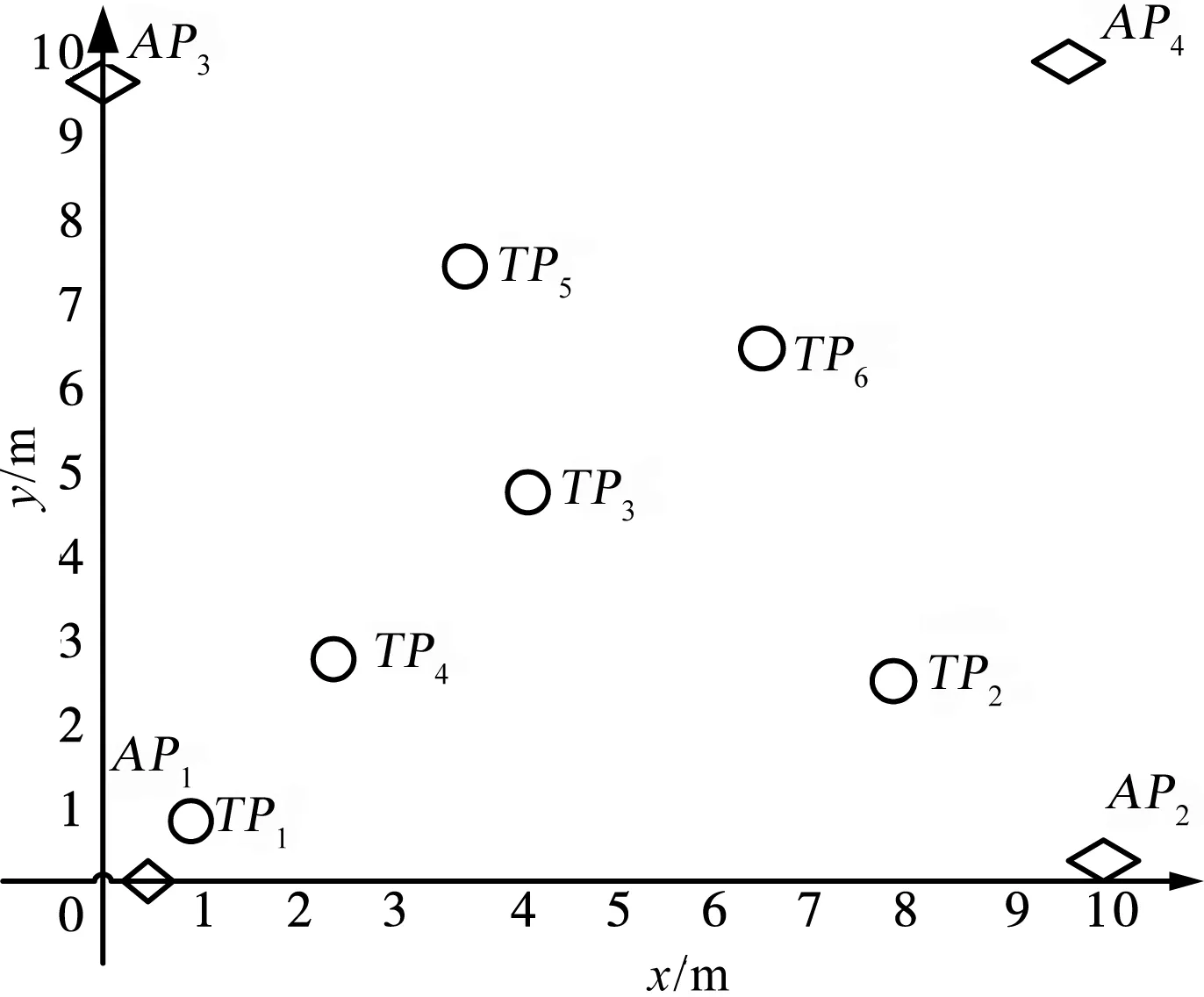
图2 在线阶段待测点位置

采用式(2)信号传播模型，各参数设置如下：

d0=1 m;PL(d0)=-62dBm;n = 2.4;

XdBm=N(0,2)。

对于改进的定位算法当k取不同值时，其定位误差如图3所示。

当k取值越小，则参考点离测试点越近，则其线性度越好，定位误差越小。如图3所示，当k=2时定位误差最大值为0.28 m，平均定位误差是0.21 m；当k= 3时，定位误差的最大值是0.68 m，平均定位误差是0.44 m；当k= 4时，定位误差的最大值是0.72 m，平均定位误差是0.48 m，理论与实际相符。综合上述，在10 m*10 m的小区域定位中，本文算法在k取2时取得最佳定位精度。以下仿真中k取值为2。

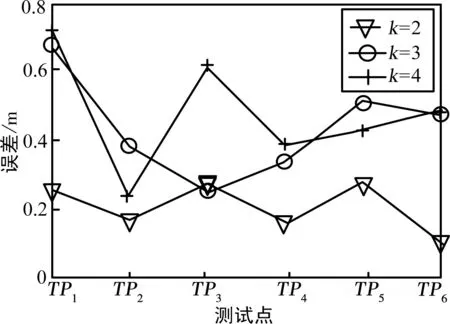
图3 改进算法在不同网络中定位误差

对于改进的算法，在不同的网络中进行仿真，其各个点的位置与网络按照同比例放大。其仿真结果如图4所示。

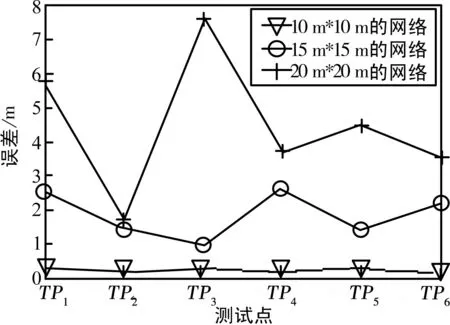
图4 不同网络定位误差

由式(2)所示，随着距离的增加，信号强度迅速减小，在10 m内，其信号强度随距离变化明显。当距离达到一定程度，距离增加，信号强度几乎不变，这就会造成其定位误差较大。

如图4所示，可以看出，随着网络规格的增大，本文算法的定位误差随之增大，在15 m*15 m大小的网络中，该算法的平均定位误差为1.86 m，在20 m*20 m的网络中，算法的平均定位误差达到了4.46 m，而在10 m*10 m大小的网络中，该算法的定位误差小于0.3 m。由上述易知，理论与实际相符，本文改进的定位算法适用于10 m*10 m的小区域定位，且具有较高的定位精度。

在10 m*10 m的网络中，分别使用最大似然估计，传统的位置指纹定位加权算法和改进的位置指纹定位算法测得待测点位置误差结果如图5所示。

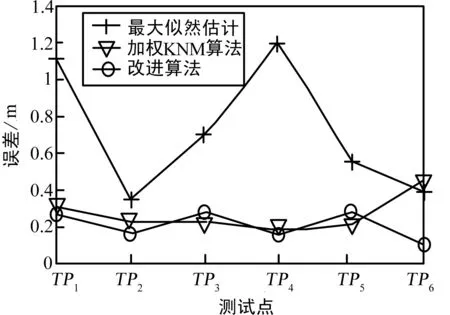
图5 不同算法测量误差

如图5所示，在k=2情况下，加权KNN算法定位误差平均值为0.35 m，而本文提出的算法定位的平均误差为0.28 m，最大似然估计算法定位的平均误差为0.7 m。相较于最大似然估计算法，本文提出的算法定位精确度提高了近60%；相较于加权KNN算法，本文提出的定位算法定位精确度提高了22.2%。综上所述，在10 m*10 m的小区域室内定位中，相较于最大似然估计和传统的位置指纹定位加权算法，本文算法降低了定位误差，提高了定位精确度。

3 结束语

本文对位置指纹定位算法在线阶段的处理数据，提出一种新算法。这种算法前期处理和传统KNN算法相同，根据欧氏距离找到与待测点最相似的k(k= 2定位误差最小)个点，之后本算法使用线性拟合的方法，算出待测点到锚节点的距离，因为锚节点坐标已知，所以列出方程组求解未知数即可得到待测点的位置，其位置定位比传统KNN算法定位精度更高。在研究过程中发现，该改进算法只适用不大于10 m*10 m的小区域网络的高精度定位，可应用于仓库管理、图书管理及物品查找等场合。当网络较大时，可以使用蜂窝技术，将大网络化为若干个小网络进行高精度定位。

[1] Rodriguez M D,Favela J,Martinez E A,et al.Location-aware Access to Hospital Information and Services[J].Information Technology in Biomedicine IEEE Transactions on,2004,8(4):448-455.

[2] Harroud H,Ahmed M,Karmouch A.Policy-driven Personalized Multimedia Services for Mobile Users[J].Mobile Computing IEEE Transactions on,2003,2(1):16-24.

[3] Krumm J,Scott J,Hazas M.Location-Aware Computing Comes of Age[J].Computer,2004,37(2):95-97.

[4] Yu F,Jiang M,Liang J,et al.An Indoor Localization of WiFi Based on Branch-bound Algorithm[C]∥ International Conference on Information Science,Electronics and Electrical Engineering.IEEE,2014:1306-1308.

[5] Serodio C,Coutinho L,Pinto H,et al.A Fuzzy Logic Approach to Indoor Location Using Fingerprinting[M].New York:Springer,2013:155-169.

[6] Seigoi I,Nobuo K.Bayesian Based Location Estimation System Using Wireless LAN[C]∥ Pervasive Computing and Communications Workshops,2005.PerCom 2005 Workshops.Third IEEE International Conference on IEEE,2005:273-278.

[7] Shin B,Lee J H,Lee T,et al.Enhanced Weighted K-nearest Neighbor Algorithm for Indoor Wi-Fi Positioning Systems[C]∥ International Conference on Computing Technology and Information Management.IEEE,2012:574-577.

[8] 刘洺辛,孙建利.基于能效的WLAN室内定位系统模型设计与实现[J].仪器仪表学报,2014,35(5):1169-1178.

[9] Abusara A,Hassan M.Enhanced Fingerprinting in WLAN-based Indoor Positioning Using Hybrid Search Techniques[C]∥ Communications,Signal Processing,and their Applications (ICCSPA),2015 International Conference on IEEE,2015:1-6.

[10]Manirabona A,Fourati L C.A Kriged Fingerprinting for Wireless Body Area Network Indoor Localization[J].Wireless Personal Communications,2014,80(4):1501-1515.

[11]高 鹏,石为人,周 伟,等.基于图论模糊聚类的室内自适应RSSI定位算法[J].仪器仪表学报,2013,34(9):1998-2004.

[12]Widyawan K M,Pesch D.Influence of Predicted and Measured Fingerprint on the Accuracy of RSSI-based Indoor Location Systems[C]∥ in Positioning,Navigation and Communication,2007.WPNC ’07.4th Workshop on 2007:145-151.

[13]Wang X,Qiu J,Ye S,et al.An Advanced Fingerprint-based Indoor Localization Scheme for WSNs[C]∥ Industrial Electronics and Applications (ICIEA),2014 IEEE 9th Conference on IEEE,2014:2164-2169.

[14]Wang B,Zhou S,Liu W,et al.Indoor Localization Based on Curve Fitting and Location Search Using Received Signal Strength[J].IEEE Transactions on Industrial Electronics,2015,62(1):572-582.

Location Fingerprint Algorithm Based on Linear Data Processing

DING Xu-xing,WANG Bing-bing

(School of Physics and Electronic Engineering,Anhui Normal University,Wuhu Anhui 241000,China)

In order to further improve the indoor positioning accuracy,the paper presents an improved location fingerprint positioning algorithm.In the offline stage,the signal strength of the sampling points is collected to build up the database.In the online stage,the linear fitting and the least square method are combined to calculate the estimated location of the test points.The result shows that the improved algorithm is especially suitable for the high-accuracy positioning of small-area networks not more than 10 m10 m.As compared with conventional fingerprinting algorithms,the average positioning error of the improved algorithm is reduced by 22.2%,and the positioning accuracy is improved.

location fingerprint algorithm;linear fitting;least square method;high-accuracy

10.3969/j.issn.1003-3114.2017.02.05

丁绪星,王兵兵.基于线性化数据处理的位置指纹算法[J].无线电通信技术,2017,43(2):21-24.

2016-10-10

国家自然科学基金项目(61401004)；安徽师范大学创新基金项目(2015cxsj121)

丁绪星(1971—)，男，博士，教授,硕士生导师，主要研究方向:物联网技术、汽车电子、数字信号处理。王兵兵(1988—)，男，硕士研究生，主要研究方向：物联网技术。

TP393

A

1003-3114(2017)02-21-4