一种新的PSWF调制信号PAPR抑制方法

毛忠阳，陆发平，刘传辉 ，康家方 ，刘 晓

(1.海军航空工程学院 电子信息工程系，山东 烟台 264001；2.山东省信号与信息处理重点实验室，山东 烟台 264001；3.装备发展部第六十一研究所，北京 100141)

一种新的PSWF调制信号PAPR抑制方法

毛忠阳1,2,3，陆发平1,2，刘传辉1,2，康家方1,2，刘 晓1,2

(1.海军航空工程学院 电子信息工程系，山东 烟台 264001；2.山东省信号与信息处理重点实验室，山东 烟台 264001；3.装备发展部第六十一研究所，北京 100141)

针对椭圆球面波(Prolate Spheroidal Wave Function,PSWF)时域正交调制信号峰均功率比(Peak-to-Average Power Ratio,PAPR)过高，易受功率放大器非线性特性影响，造成PSWF脉冲间良好正交性下降，导致系统解调性能下降的问题，引入A律压缩，提出了一种基于A律压缩的PSWF调制信号PAPR抑制方法。该方法能够有效抑制PSWF调制信号PAPR，改善经过功放后调制信号的功率谱和系统误码性能。

椭圆球面波；峰均比；压扩算法；自适应

0 引言

椭圆球面波函数是Bell实验室D.Slepian等人于1961年定义的一类特殊函数的集合[1]，在通信[2-3]、流体动力学[4]及滤波[5-6]等领域得到广泛应用。在无线电通信领域，2008年专利“非正弦时域正交调制方法”公布了一种基于PSWF的非正弦时域正交调制方法[7]，采用时域波形叠加、频域频谱交叠的方式，有效提高了频带利用率。但PSWF调制信号峰均功率比(Peak-to-Average Power Ratio,PAPR)较高，应用于卫星通信系统时，易受PA非线性特性影响，造成信号非线性失真，从而降低系统性能。

针对此问题，舒根春等[8]从调制符号角度出发，提出了一种基于调制符号选择的PSWF调制信号PAPR抑制方法，陈昭男等[9]从正交PSWF脉冲集的特征向量加权表示入手，提出了一种基于Givens旋转的PAPR抑制方法，但存在对调制信号的PAPR抑制能力有限、算法复杂度较高的问题。文献[10]引入μ律压缩，给出了一种自适应PAPR抑制方法，但由于该方法是一种非线性变换，存在对PSWF脉冲间良好正交性影响较大的问题。

1 基于A律压缩的PAPR抑制方法

目前，功放模型主要分为无记忆PA模型和有记忆PA模型2大类，暂不考虑PA的记忆效应，选用广泛应用于卫星通信系统中的Saleh模型[11]。Saleh模型是根据对行波管功率放大器TWTA的输入、输出数据进行统计分析后得到的，其AM-AM和AM-PM特性分别为：

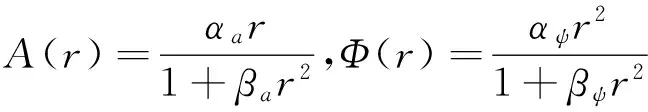
(1)

式中，r为输入信号的幅度，αa、βa、αψ、βψ为功放模型参数。由式(1)可知，随着输入信号幅值的增大，信号非线性失真越来越严重。

PAPR是衡量调制信号进入功放饱和区时，受PA影响非线性失真程度的重要指标，离散信号的PAPR定义为一个码元时间内信号的峰值功率与其平均功率的比值[12-13]。功放输入回退(InputBackOff,IBO)[14]是衡量功放效率的重要指标，IBO越小，功放效率越高，当功放达到饱和且输入信号功率一定时，随着输入信号平均功率的增大，IBO不断降低，功放效率越来越高，但由式可知，功放对调制信号的非线性影响也越来越大。

A律压缩是由ITU-TCCITTG.712定义的关于脉冲编码的一种压缩算法[15]，对于幅值归一化的信号而言，其表达式为：

y(n)=

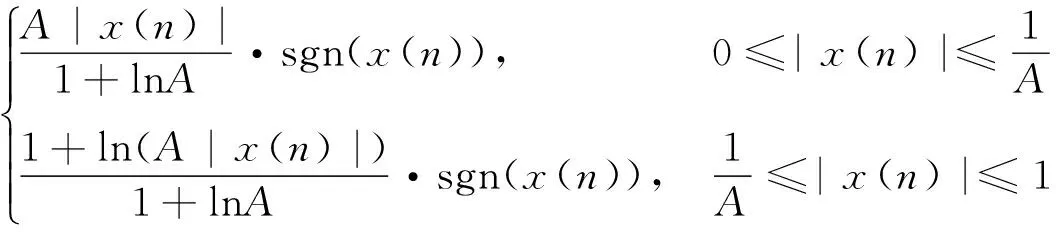
(2)

式中，sgn(·)为符号函数，x(n)和y(n)分别为输入电压和输出电压，A为压缩参数。

由式(1)可知，功放对调制信号的非线性影响，与调制信号的峰值、平均功率及峰均功率比密切相关，且峰值和平均功率直接决定信号PAPR。因此，有必要对A律压缩对PSWF调制信号峰值和平均功率的影响机理进行研究。

基于上述分析，首先，分析A律压缩参数对信号峰值和平均功率的影响机理，分析A律压缩对PSWF调制信号PAPR的抑制能力；其次，设计可调增益K(μ,s)、K(μ,s)根据输入信号自适应调节，保证压缩前后调制信号平均功率不变，在此基础上，提出基于A律压缩的PSWF调制信号PAPR抑制算法，并构建算法实现模型。

1.1 压缩参数对信号峰值的影响

由式(2)可知，当0≤|x(n)|≤1/A时：

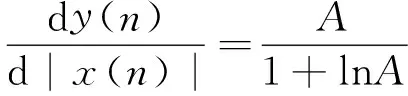
(3)

且A≥1，因此，

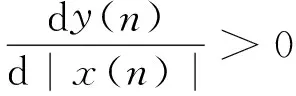
(4)

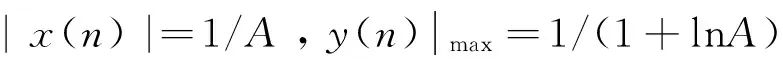
1.2 压缩参数对信号平均功率的影响

定义A律压缩前后，PSWF调制信号平均功率的差值为：

ΔP=Paf-Pbf，

(5)

式中，Paf为压缩后信号平均功率，Pbf为压缩前信号平均功率。结合式(2)，式(5)可以表示为：

(6)

结合A律压缩对调制信号分段压缩的特点，为便于理论分析，分2部分对ΔP进行分析。对于第1部分，令：

(7)

求导得：

(8)

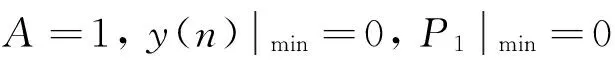
对于第2部分，令：

(9)

求导得：

(10)

同时，对于幅值归一化的PSWF调制信号，|x(n)|max=1，因此，dP2/dA>0。这表明A律压缩后，信号幅值在1/A≤|x(n)|≤1的信号分量的平均功率增加，随着参数A的增大不断增大。

通过上述分析可知，经过A律压缩，PSWF调制信号的峰值不变，信号的平均功率随着参数A的增大不断增大。同时，A律压缩能够有效降低调制信号PAPR，提高功放效率。但A律压缩后，对于幅值归一化的PSWF调制信号，信号中大幅值分量所占比例增加，由式(1)可知，此时，调制信号受功放非线性影响的幅值分量增加，加剧调制信号的非线性失真程度。这表明A律压缩降低信号PAPR、提高功放效率，是以增加信号中大幅值分量所占比例，增加调制信号非线性失真程度为代价的。同时，要有效抑制调制信号PAPR，需要较大的A值，但当参数A取值较大时，压缩后调制信号的平均功率较大、IBO较小，存在调制信号非线性失真程度增加的问题。

1.3 基于A律压缩的PAPR抑制算法

针对上述问题，考虑到对调制信号进行线性增益前后调制信号PAPR不变，因此，对压缩后调制信号进行线性增益，适当进行功率回退，保证有效抑制调制信号PAPR，压缩前后信号平均功率不变的前提下，降低压缩后信号中大幅值分量的比例；同时，由式(2)可知，压缩后信号平均功率随着压缩参数A、调制信号的变化而不断变化，因此，增益需要根据压缩参数、输入信号的变化而变化。基于上述分析，在式(2)的基础上添加可调增益K(μ,x)，令K2(u,x)等于压缩前后调制信号平均功率的比值，即：

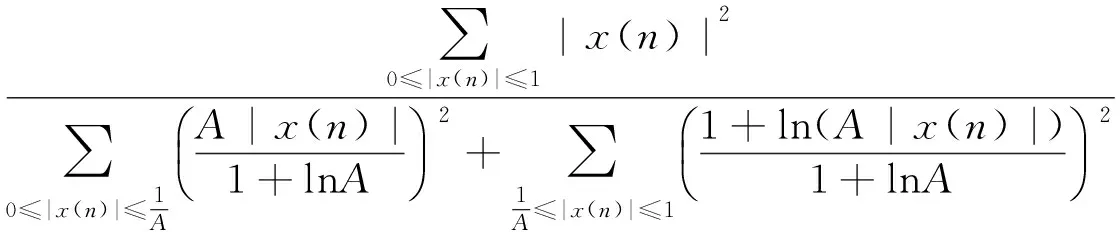
(11)

按照式(11)，K(u,x)根据压缩参数、输入信号自适应调节，在保证压缩前后信号平均功率不变的墙体下，降低压缩后信号中大幅值分量的比例。同时，由1.1节和1.2节可知，添加可调增益K(u,x)后，随着压缩参数A的增加，压缩后调制信号的峰值不断降低。

基于上述分析，对A律压缩进行改进，提出了一种基于A律压缩的自适应PSWF调制信号PAPR抑制算法，简称自适应压扩算法，其表达式为：

y(n)=

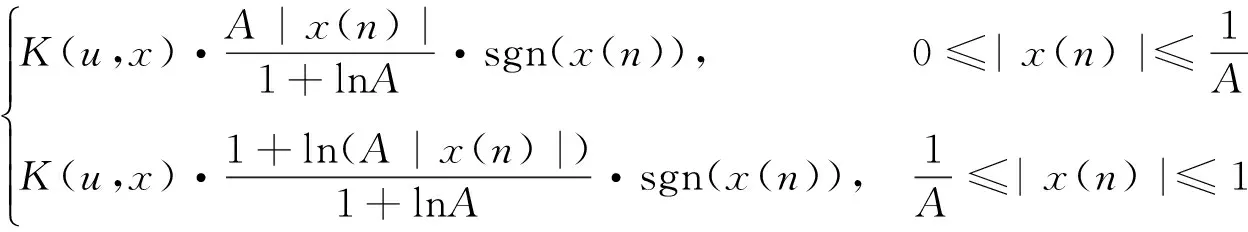
(12)

由式(12)可知，对接收信号进行解压时，需要分段处理，且功放的非线性特性、噪声的随机性均会对给调制信号带来干扰，对接收信号进行解压，存在归属区域不易区分的问题，导致PSWF脉冲间良好的正交性进一步遭到破坏，严重降低系统的解调性能。因此，若能够在接收端直接对压缩PSWF调制信号进行解调，即可避免信号进行解压对脉冲组间正交性的进一步破坏，这给式中压缩参数A的取值带来了较高的要求。那么压缩参数A对PSWF脉冲间正交性有何影响？其取值应遵循怎样的规则？

2 PAPR抑制方法系统模型构建

在第1节的基础上，针对接收信号进行解压时，归属区域不易区分的问题，在分析所提方法对PSWF调制信号PAPR、PSWF脉冲组正交性影响的基础上，构建PAPR抑制方法系统模型。该模型在接收端直接对调制信号进行检测，有效解决了对接收信号进行解压，存在归属区域不易区分的问题。

2.1 PAPR抑制方法对信号PAPR影响

由于对调制信号进行线性增益前后，调制信号PAPR不变，故本文所提PAPR抑制方法对信号PAPR的抑制能力与原A律压缩相同。定义PSWF调制信号压缩前后PAPR的比值为α，即：

(13)

同时，由于A律压缩前后信号的峰值不发生变化，结合式(5)，式(13)可以化简为：

(14)

由式(14)可知，对于PSWF调制信号x(n)，其功率Paf为定值，α的数值与ΔP密切相关，且由式(8)和式(10)可知，ΔP随着参数A的增大不断增大，因此，α随着参数A的增大不断增大。这表明本文所提PAPR抑制方法对信号PAPR的抑制能力，随着参数A的增大不断增强。

2.2 PAPR抑制方法对脉冲组正交性影响

目前，对PSWF调制信号的解调主要采用相干解调，PSWF脉冲组间良好的正交性是调制信号正确解调的关键，而自适应压扩算法是一种非线性运算，因此会对PSWF脉冲间良好的正交性造成一定的破坏，影响系统解调性能。那么自适应压扩算法对PSWF脉冲间正交性呈现出怎样的影响？

假设x(n),n=1,2…,N为压缩前调制信号，压缩后调制信号为y(n),n=1,2…,N，其表达式为式(12)，PSWF脉冲组正交性与参数A存在如下关系：

当0≤|x(n)|≤1/A时：

(15)

这表明信号幅值在0≤|x(n)|≤1/A的分量，压缩前后信号称线性关系，不会对PSWF脉冲组正交性造成任何影响。

当1/A≤|x(n)|≤1时：

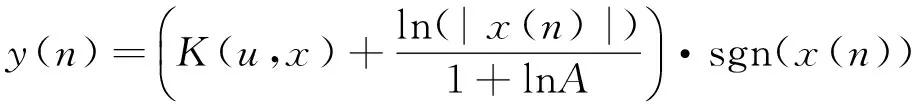
(16)

这表明信号幅值在1/A≤|x(n)|≤1的分量，压缩前后信号称非线性关系，会导致PSWF脉冲组良好正交性下降。

通过上述分析可知，自适应压扩算法对信号中大幅值分量非线性影响较大，随着参数A的增加，影响程度不断增加，相应的对PSWF脉冲组良好正交性破坏程度不断加剧。因此，要在接收端对压缩后的调制信号直接解调，需要用较小的A值。

2.3 构建算法系统实现模型

PAPR抑制方法系统模型如图1所示，主要由A律压缩函数模块、参数A设置模块、K(μ,x)计算模块和乘法模块4个模块构成。主要模块构建思路和功能如下：

A律压缩函数模块：对信号进行压缩处理。根据式(12)对调制信号进行压缩处理，计算信号y1(n)，降低调制信号PAPR。

参数A设置模块：设置参数A的取值。根据实际应用条件，设置参数A，保证压缩后PSWF脉冲组间仍具有良好的正交性。

K(u,x)计算模块：获取参数K(u,x)的取值。根据式(11)计算可调增益K(u,x)，根据输入信号和压缩参数自适应调节K(u,x)，保证压缩前后信号平均功率不变。

乘法模块：对PSWF调制信号进行功率回退。将A律压缩函数模块获得的信号y1(n)，与K(u,x)计算模块获得的K(u,x)相乘，计算自适应压扩算法的输出信号y(n)。

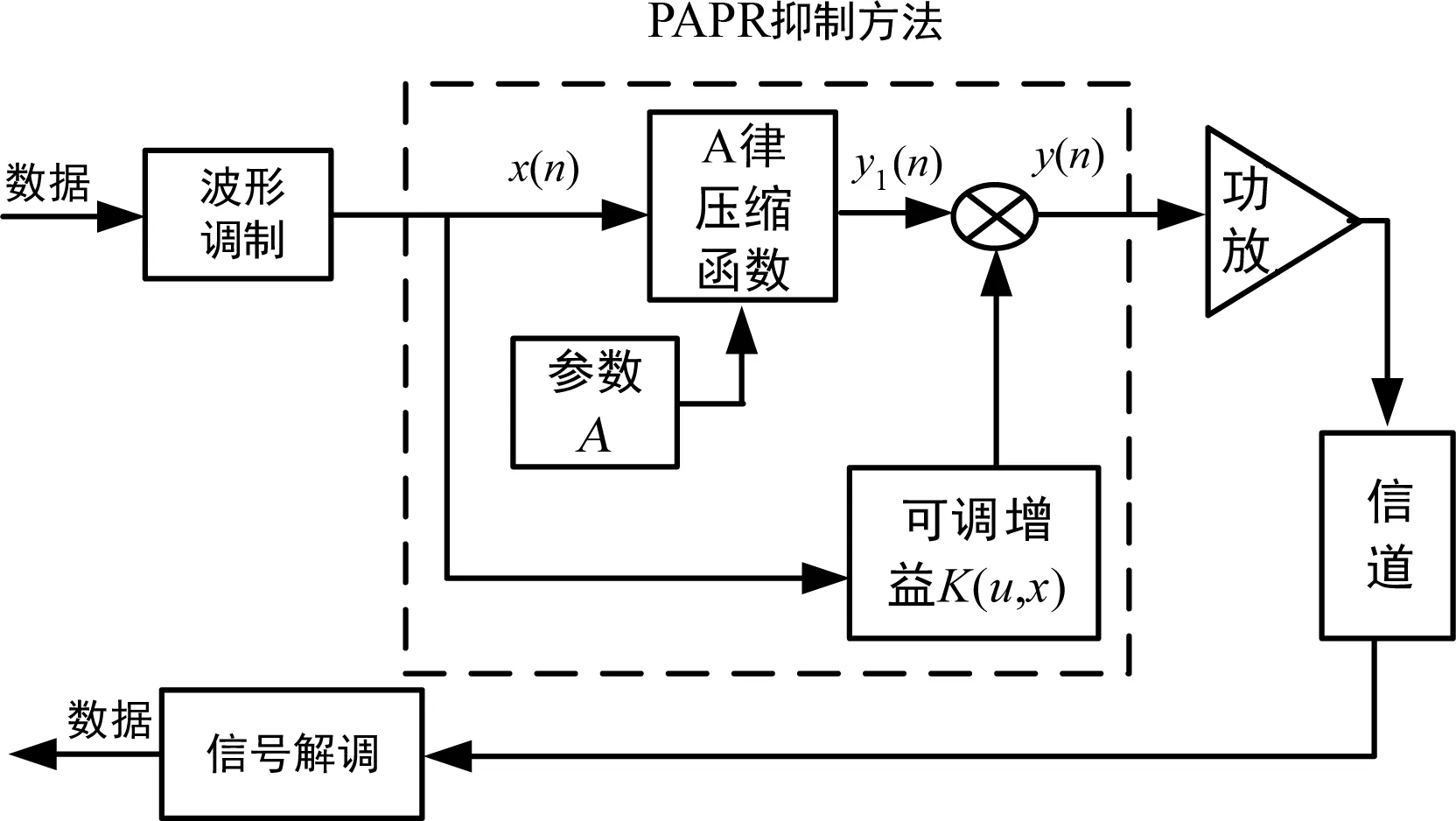
图1 自适应压扩算法实现模型

3 仿真分析

在Matlab仿真环境下，对自适应压扩算法对PSWF调制信号峰值和平均功率、脉冲间正交性的影响以及PAPR抑制能力进行仿真分析，验证理论分析的准确性。同时，仿真分析PA自适应压扩算法对PSWF调制信号的功率谱以及系统误码性能的影响，说明自适应压扩算法降低PA对调制信号非线性影响的有效性。为更好地分析算法对PSWF调制信号正交性和功率谱的影响，说明所给PAPR抑制方法在降低PA对信号非线性影响的有效性，仿真时将频带划分为多个子波带，选用无记忆PA模型Saleh模型。

3.1 仿真条件

① 调制信号：频带1～1.1MHz，划分为4个子波带，频谱交叠度为50%，时间带宽积c=4 Hz·s，每个子波带按能量聚集性由高到低，取前2阶PSWF脉冲，叠加生成非正弦时域正交调制信号，并对调制信号幅值进行归一化处理；

② 功率放大器：选用Saleh模型，其AM-AM和AM-PM特性分别如式(1)所示，式中，参数取经典值αa=2、βa=1、αψ=π、βψ=1[11]。

3.2 仿真结果与分析

图2为前2个子波带，每个子波带按能量聚集性由高到低，取前2阶PSWF脉冲，叠加生成非正弦时域正交调制信号，压缩前后信号峰值和平均功率随参数A变化曲线。

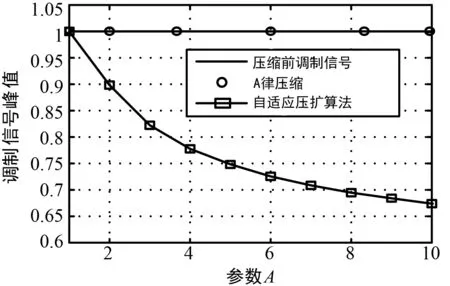
(a) 信号峰值随参数A变化曲线

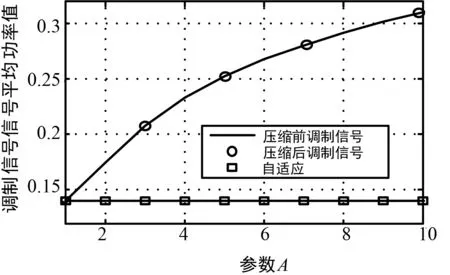
(b) 信号平均功率随参数A变化曲线图2 压缩前后信号峰值和平均功率随参数A变化曲线

其中，图2(a)为压缩前后峰值随参数A的变化曲线，由仿真结果可知，自适应压扩算法能够有效压缩调制信号峰值，且随着参数A值的增加，对调制信号峰值的抑制能力越来越大，有效降低压缩后调制信号中大幅值分量的比例，与理论分析一致。这表明提出的自适应压扩算法，能够有效解决A律压缩降低信号PAPR、提高功放效率，从而增加信号中大幅值分量所占比例，增加调制信号非线性失真程度为代价的问题。图2(b)为PSWF调制信号压缩前后平均功率随参数A的变化曲线，由仿真结果可知，调制信号经过自适应压扩算法压缩前后信号平均功率相同，保证压缩前后功放IBO不变，保证PA有较高的功放效率，能够实现预期的目标，与理论分析一致。

3.2.1 调制信号功率谱

与图2仿真结果相同，图3为PSWF调制信号归一化功率谱，从图3(a)中可知，当A>1时，自适应压扩算法使信号频谱发生了扩展。当A=2时，带外失真达到了约20dB，且随着参数A的增加，失真越来越严重。同时，从图3(b)中可知，当A>1时，调制信号压缩后通过PA，较直接经过PA的功放失真信号，功率谱得到一定程度的改善。当A=2时，带外失真降低了约0.5dB，且随着参数A的增加，改善程度不断提高。这表明由于自适应压扩算法是一种非线性算法，导致调制信号有一定程度的失真；但算法能够有效抑制调制信号PAPR，在一定程度上抑制PA对信号的非线性影响，改善调制信号频谱。

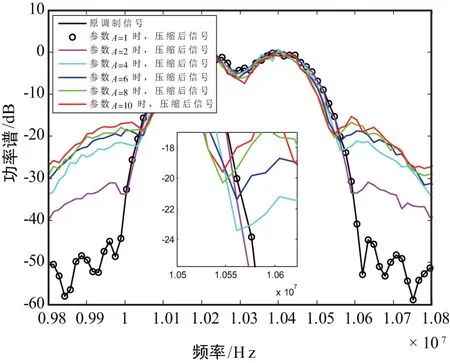
(a) 压缩后调制信号功率谱

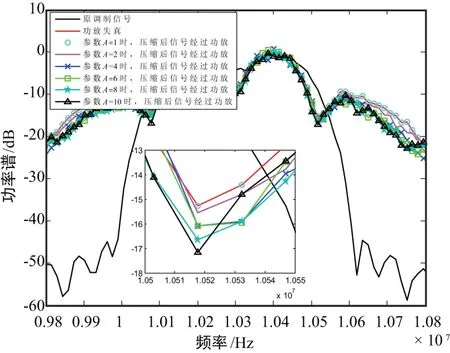
(b) 调制信号经过PA后功率谱图3 调制信号功率谱

3.2.2 不同参数μ的PAPR抑制特性

互补累计分布函数[16](ComplementaryCumulativeDistributionFunction，CCDF)定义为信号PAPR超过某一门限的概率，用来衡量调制信号PAPR统计特性。与图2仿真结果相同，图4是自适应压扩算法在不同参数A时，压缩前后调制信号CCDF曲线，由仿真结果可知，提出的自适应压扩算法能够有效抑制调制信号PAPR，当A=2，CCDF=10-4时，经过自适应压扩算法压缩前后，PSWF调制信号PAPR分别为8.6 dB和7.7 dB，与原调制信号相比，压缩后调制信号PAPR降低约0.9 dB；同时，随着参数A的增加，抑制PAPR的能力越来越强，这表明提出的自适应压扩算法能够有效抑制PSWF调制信号PAPR，与理论分析一致。

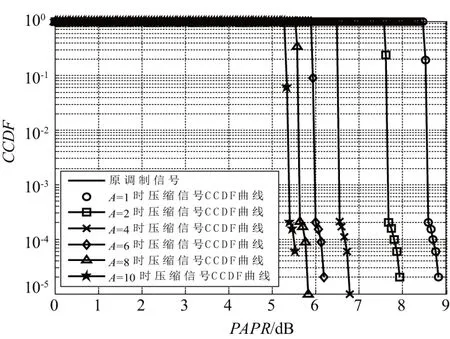
图4 算法PAPR抑制特性曲线

3.2.3 系统误码性能

图5是解调方式采用相关解调的条件下，采用自适应压扩算法前后，不同参数A、并行脉冲路数时，系统误比特率性能仿真曲线。由仿真结果可知，提出的算法能够一定程度上降低PA造成的信号带内失真，提高系统误码性能。

由图5(a)可知，当参数A=2、误比特率BER=3×10-3时，较直接经过PA的功放失真信号相比，采用自适应压扩算法系统性能提高约4 dB；相对于未经放大器失真的调制信号，当误比特率为10-5时，所需Eb/N0仅增加约0.3 dB。但随着参数A的增加，由于自适应压扩算法给PSWF脉冲间良好正交性带来的破坏程度，超过PA带来的破坏程度，算法对系统误码性能的改善能力不断降低。

同时，由图5(b)可知，在不同PSWF脉冲并行路数条件下，自适应压扩算法对系统误码性能的改善程度不同，当参数A=2时，随着并行脉冲路数的增加，所提算法对系统误码性能的改善能力不断降低。这表明由于所提算法是一种非线性运算，会导致调制信号有一定程度的失真，且补偿带外失真的能力相对较弱，随着子波带的增加，相邻子波带之间的干扰增大，降低系统误码性能。

通过上述分析可知，本文所给自适应压扩算法能够在保证压缩前后信号平均功率不变的前提下，有效降低压缩后调制信号中大幅值分量的比例，抑制调制信号PAPR，降低PA对调制信号的非线性影响，在一定程度上改善调制信号功率谱，提高系统误码性能。

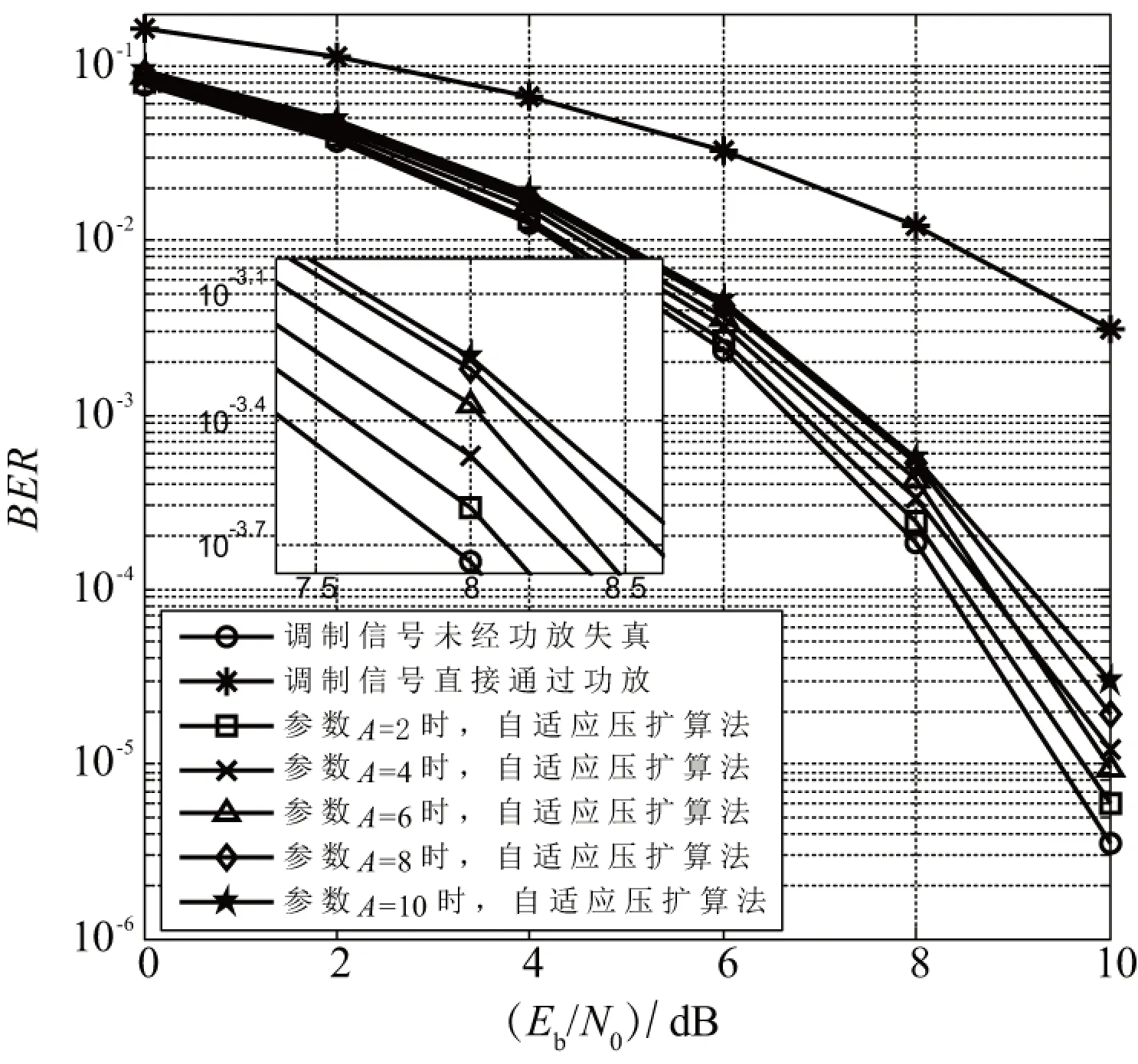
(a) 并行路数为4时,不同参数A

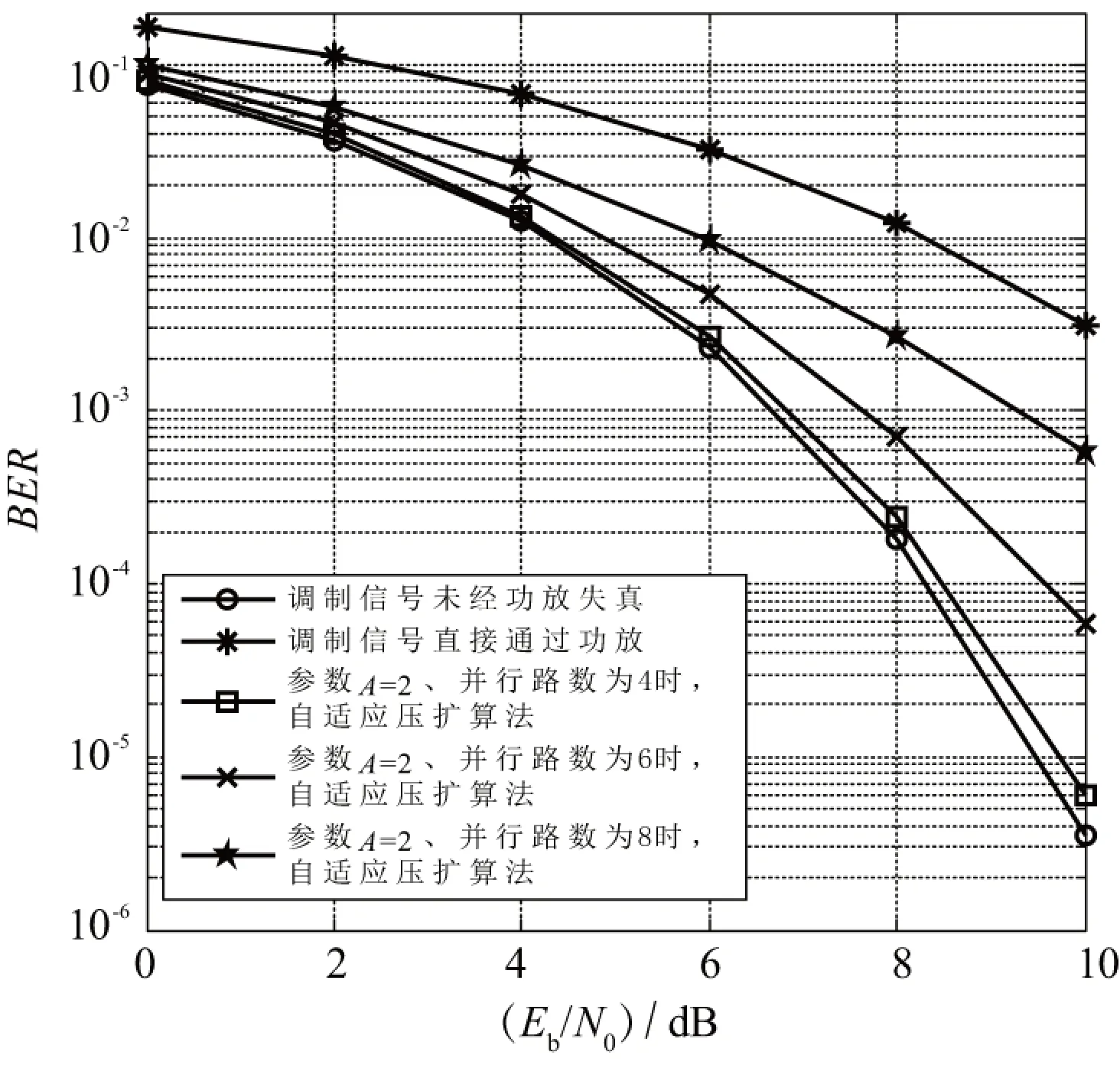
(b) 参数A=2时,不同并行路数图5 系统误码率性能比较

4 结束语

针对PSWF调制信号PAPR较高，易受PA非线性影响的问题，结合A律压缩，在分析参数A对调制信号峰值和平均功率影响机理的基础上，提出了一种基于A律压缩的PSWF调制信号PAPR抑制方法，并构建了系统实现模型，为基于A律压缩的峰均比抑制方法适用性提升、参数优化提供了理论指导。需要特别说明的是，在本文3.1节仿真条件下，A=2时，系统具有较好的误码性能，如果应用场景发生变化，参数A的取值也会相应发生变化。同时，由于所提算法是一种非线性运算，会导致调制信号有一定程度的失真，且补偿带外失真的能力相对较弱。随着子波带的增加，相邻子波带之间的干扰不断增大，降低系统误码性能。如何抑制压缩后信号带外失真，降低相邻子波带之间的干扰，提高系统误码性能，将是我们后续工作的关注重点。

[1] Flammer C.Spheroidal Wave Functions[M].California：Stanford University Press,1956：16-19.

[2] 赵志勇,王红星,刘锡国,等.正交椭圆球面波函数脉冲调制方法[J].电子与信息学报,2012,34(10)：2331-2335.

[3] 陈昭男,王红星,赵志勇,等.基于正交PSWF的DS-BPSK多址调制方法[J].无线电工程,2010,40(4)：19-21.[4] Osipove A,Rokhlin V.On the Evaluation of Prolate Spheroidal Wave Functions and Associated Quadrature Rules[J].Appliedand Computational Harmonic Analysis,2013,36(1)：108-142.

[5] Neves L C,Araujo G M,Costa J C D,et al.Design of a PSWF Impulse Response Filter for UWB Systems[C]∥2012 IEEE International Symposium on Circuits & Systems(ISCAS),2012：1935-1938.

[6] 刘 晓,王红星,刘传辉,等.基于椭圆球面波函数的数字带通滤波器设计[J].电讯技术,2016,56(2)：176-182.

[7] 王红星,赵志勇,刘锡国,等.非正弦时域正交调制方法[P].中国,ZL200810159238.3,2011-02-02.

[8] 舒根春,王红星.降低基于PSWF的非正弦调制信号PAR方法[J].信息传输与接入技术,2011,37(1)：22-24.

[9] 陈昭男,王红星,钟佩琳,等.基于Givens旋转变换的PSWF调制信号PAPR抑制方法[J].电子与信息学报,2013,35(6)：1406-1412.

[10] 王红星，陆发平,刘传辉,等.一种椭圆球面波调制信号自适应峰均比抑制方法[J].电子与信息学报,2017，39(1)：75-81.

[11] Saleh A A M.Frequency-independent and Frequency-dependent Nonlinear Models of TWT Amplifiers[J].IEEE Trans Communications,1981,29(11)：1715-1720.

[12] 杨 超,王 勇,葛建华.联合迭代滤波与压扩参数优化的OFDM 信号峰平比抑制[J].通信学报,2015,36(4)：2515-2520.

[13] 车 轩,胡铁森,张 敏.一种OFDM系统PAPR抑制技术联合算法研究[J].无线电通信技术,2015,41(2)：29-31.

[14] JIANG T，WU Y Y.An Overview：Peak-to-Average Power Ratio Reduction Techniques for OFDM Signals [J].IEEE Transactions on Broadcasting,2011,54(2)：257-268.

[15] 扈 鹏.OFDM系统中降低峰均功率比算法的研究[J].无线电工程,2012,42(7)：55-58.

[16] 吕晓凯,胡铁森,万仁峰,等.MIMO-OFDM系统峰均比抑制技术的研究[J].无线电通信技术,2013,39(1)：49-51.

A New PAPR Reduction Method for PSWF Orthogonal Modulation Signal

MAO Zhong-yang1,2,3,LU Fa-ping1,2,LIU Chuan-hui1,2,KANG Jia-fang1,2,LIU Xiao1,2

(1.Department of Electrical and Information Engineering,Naval Aeronautical and Astronautical University,Yantai Shandong 264001,China;2.Key Laboratory on Signal & Information Processing of Shandong Province,Yantai Shandong 264001,China;3.China Electronic System Corp.,Beijing 100141,China)

A new companding transform based on A-law companding schemes is proposed for the reduction of Peak-to-Average Power Ratio(PAPR) of Prolate Spheroidal Wave Function(PSWF) orthogonal modulation signal,which causes serious degradation in performance when a nonlinear power amplifier(PA) is used.Both the mathematical deduction and simulation result show that the proposed method can effectively reduce PAPR of PSWF orthogonal modulation signal,improve the power spectrum of the signal,and effectively improve the bit error rate performance of system.

prolate spheroidal wave function;peak-to-average power ratio;companding transform;adaptive

10.3969/j.issn.1003-3114.2017.02.02

毛忠阳,陆发平,刘传辉,等.一种新的PSWF调制信号PAPR抑制方法[J].无线电通信技术,2017,43(2)：06-11,20.

2016-11-15

山东省“泰山学者”建设工程专项经费基金资助项目(ts20081130)；中国博士后科学基金特别资助项目(2016T91018)

毛忠阳(1979—)，男，副教授，主要研究方向：现代通信系统、非正弦波通信、无线光通信等。陆发平(1991—)，男，博士研究生，主要研究方向：现代通信系统、非正弦波通信。

TN911.7

A

1003-3114(2017)02-06-6