双钟摆主被动悬架式大型喷雾机喷杆动力学仿真与试验
2017-03-02崔龙飞薛新宇丁素明乐飞翔
崔龙飞 薛新宇 丁素明 顾 伟 陈 晨 乐飞翔
(1.农业部南京农业机械化研究所, 南京 210014; 2.江苏大学现代农业装备与技术教育部重点实验室, 镇江 212013)
双钟摆主被动悬架式大型喷雾机喷杆动力学仿真与试验
崔龙飞1,2薛新宇1丁素明1顾 伟1陈 晨1乐飞翔1
(1.农业部南京农业机械化研究所, 南京 210014; 2.江苏大学现代农业装备与技术教育部重点实验室, 镇江 212013)
大型喷杆式喷雾机在田间作业时,喷杆运动严重影响了喷雾分布,悬架系统是控制喷杆动力学行为的关键装置,既要隔离来自车体的高频扰动,又要使喷杆跟踪低频的地面坡度变化,时刻保持与地面(或作物冠层)平行。为了研究双钟摆主、被动悬架机构的动力学特性,综合考虑车体运动耦合作用、地形坡度变化、摩擦等因素,使用第二类拉格朗日动力学方法建立描述喷杆动力学行为的数学模型。首先进行被动悬架动态特性研究,分析阻尼、摩擦、摆钟长度等因素对响应特性的影响;然后建立基于液压比例控制的主动悬架Matlab/Simulink仿真模型,揭示控制系统增益系数、时间常数、悬架结构参数等对喷杆响应特性、跟踪误差的影响规律。利用Stewart六自由度运动模拟平台及动态测试系统,对28 m大型喷杆悬架系统进行瞬态响应测试和频响测试,频响试验值与数学模型预测值均方根误差为0.087,表明模型可用于预测喷杆动态响应特性,指导悬架参数科学配置。
喷杆式喷雾机; 悬架; 动力学分析; 仿真; 试验
引言
喷杆式喷雾机雾化效果好、喷幅宽、作业效率高,是一种高效的大田植保机械[1],随着我国土地流转和农业机械化的推进,喷杆喷雾机逐渐大型化,由于喷杆臂展长、柔性大,在各种田间作业时,受到地面不平整、车速变化、药液晃动等随机因素的影响,易产生倾斜和振动[2],造成喷头与作物高度发生变化,致使施药质量下降、喷杆易于损坏的问题日益突出[3-5],主要原因是喷杆悬架设计理论与减振技术不完善,因此研究喷杆-悬架系统的动力学行为,为悬架设计及参数合理匹配提供理论依据,对提高喷杆喷雾均匀性有重要意义。
被动悬架主要用于衰减来自车体的运动干扰[6],不能实现地形跟踪,当扰动激励与悬架固有频率接近时易产生共振,但相关研究[7-9]很少关注悬架机构的固有频率及频响特性;喷杆主动悬架的研究[10-15]多采用距离传感器检测喷杆与作物冠层之间倾斜角度作为反馈,调整液压缸的流量和方向实现喷杆位姿的控制[16-18],但没有考虑车体运动耦合干扰(即车体姿态没有作为控制的反馈),田间车体晃动较大时喷杆地形跟踪精度较低。
综合被动、主动悬架的优点及相关研究成果[19-20],本文提出一种双钟摆主-被动悬架(被动部分隔离来自车体的高频扰动,主动部分使喷杆跟踪低频的地面坡度变化),将车体、悬架、喷杆作为一个动力学系统,考虑车体耦合运动以及摩擦的影响,使用第二类拉格朗日法建立描述喷杆动力学行为的高阶微分方程组,首先进行被动悬架动态特性分析与优化,然后根据系统动力学模型进行比例位置伺服控制理论和仿真研究,阐明控制系统增益系数、时间常量、悬架结构参数等对响应特性的影响规律。并利用Stewart六自由度运动模拟平台,对数学模型进行试验验证。
1 双钟摆主、被动悬架
喷雾机及双钟摆主、被动悬架系统如图1所示。利用物理单摆原理,根据喷杆的重心位置变化进行自动平衡,通常由两级钟摆(摆杆P1P2和摆杆P2R2)组成,R2为喷杆质心,第1级钟摆与机架铰接于P1,弹簧阻尼器2连接单摆P1P2和机身,组成被动悬架,衰减车体的扰动;第2级钟摆与第1级单摆铰接于P2,液压缸4铰接在第1级钟摆和第2级钟摆之间,液压缸的伸缩可以连续改变P1P2和P2R2的夹角,采用2个超声波传感器5检测喷杆6两端与地面7(冠层)之间的高度差,来获得喷杆相对于地面(冠层)的倾斜角度,通过伺服阀调整液压缸的流量和方向来实现喷杆位姿的控制,从而使喷杆实时与地面(冠层)保持平行,提高喷雾的均匀性。

图1 喷雾机与钟摆悬架系统Fig.1 Sprayer and pendulum suspension system1.车体 2.弹簧阻尼器 3.摆杆 4.液压缸 5.距离传感器 6.喷杆 7.地面
图2为喷杆喷雾机原理图,图中L表示液压缸的长度,L1表示第1级钟摆P1P2的长度,L2表示第2级钟摆P2R2的长度,L3表示车体质心到地面的距离,L4表示转轴P1到地面的距离,L5表示车体质心到一侧车轮的垂直距离,L6表示转轴P2到液压缸铰接点的长度。α表示喷雾机与水平线的夹角,β为喷杆与水平线的夹角,γ为地面与水平线的夹角。φ为第1级钟摆P1P2与竖直线的夹角,θ为第2级钟摆P2R2与第1级钟摆P1P2夹角。
底盘悬架和轮胎使用弹簧和阻尼器来表示,地平面用线G1G2表示,可以绕点O沿垂直纸面方向转动。车的重心为R1,喷杆的重心为R2,大量的研究表明导致喷杆不规律运动的主要原因是:车辆在通过起伏不平的路面时发生侧倾运动。因此,喷雾机底盘的运动可简化为绕瞬时中心O的转动。由于主要关心的是喷雾机作业时喷杆的翻滚(侧倾)运动,因此假设喷杆在垂直于车身纵轴的平面内运动。地面的起伏激励通过轮胎传递给车架,喷杆通过铰链连接的连杆、P2R2悬置于车架上。

图2 系统等效建模示意图Fig.2 Schematic diagram of sprayer and suspension
喷杆的质心在R2,如果θ角固定不变,该悬架是被动悬架,悬架只能绕P1点旋转。而主动液压缸连接于摆杆P1P2和P2R2之间,如果液压缸的伸缩量连续可控,θ角连续可控,当喷雾机通过起伏地面时,喷杆就能够始终与倾斜的地面平行。
2 悬架数学模型
2.1 被动悬架建模
设车体质量为M1,沿O轴的转动惯量为I1;轮胎及悬架刚度为K1,阻尼系数为C1,喷杆质量为M2,转动惯量为I2,被动悬架的阻尼系数为C2,绕轴P1的摩擦力矩为F2。
在被动模式下,喷杆悬架的行为用频响应函数H(φ/α)描述,喷杆运动的关系式可以用广义坐标φ下的第二类含耗散函数的拉格朗日方程表示,表示形式为
(1)
系统总动能TL包括喷杆转动的动能和喷杆平动的动能,即
(2)
系统的势能VL为
VL=[L4cosα-(L1+L2)cosφ]M2g
(3)
系统瑞利耗散函数DL为
(4)
在坐标φ下的广义力Qφ=0。将式(2)~(4)代入式(1)并进行拉氏变换,由于角度α和φ比较小,喷杆与水平面夹角β=φ,sinα≈α,cosα≈1,可得动力学系统传递函数
(5)
被动悬架系统属于二阶系统,系统的阻尼比ζ为
(6)
系统固有频率ωn为
(7)
系统的阻尼频率为
(8)
2.2 主动悬架建模
研究主动悬架喷杆动态特性,需要考虑喷雾机在起伏路面行驶时的翻滚运动,故将底盘、悬架、喷杆作为一个整体系统进行动力学分析,系统竖直面内有3个自由度,仅用一个液压缸驱动,属多输入单输出、欠驱动系统,喷杆的运动可以用广义坐标系(α,φ,β)下的拉格朗日方程描述,即
(9)
(10)
(11)
底盘、喷杆系统的总动能TL为
(12)
式中前两项是底盘平动和转动的动能,第3项是喷杆转动动能,第4项和第5项是喷杆平动动能。
系统的势能
(13)
系统瑞利耗散函数
(14)
系统的广义力矩:Qα=0、Qφ=-F和Qβ=F。
将系统动能、势能、瑞利耗散函数等分别代入公式(9)~(11)中,F为执行器产生的力矩,假设α、β、φ、γ都非常小,忽略二阶项,可以得到描述喷杆运动的方程组为
(15)
(16)
(17)
从图2悬架几何关系可以得出油缸的伸缩量
(18)
通过方程(15)~(18)描述在车体扰动、地形坡度变化、油缸伸缩等输入下的喷杆动力学特性;也可以在车体倾角、地形坡度、喷杆倾角测得的情况下,通过方程组进行动力学逆解,解算出液压缸动作的位移和推力,为下一步进行喷杆位置伺服控制理论和仿真研究奠定基础。
3 被动悬架动态特性仿真分析
建立钟摆式被动悬架和主动悬架的数学模型后,将通过模型分析系统参数对喷杆动力学行为的影响机理,指导悬架的设计。喷杆悬架动力学模型中的参量按照12 m喷雾机近似选取,设运载底盘及车体的质量M1=4 800 kg,沿O轴的转动惯量I1=5 000 kg·m2,轮胎刚度K1=3.2×105N/m,阻尼系数C1=2 800 N·s/m,钟摆悬架各连杆长度L3=0.9 m,L4=1.4 m,L5=1.0 m,喷杆质量M2=200 kg,转动惯量I2=1 200 kg·m2。
3.1 阶跃响应分析
喷雾机在田间作业过程中,经常会遇到一侧轮胎碾过地面凸起,车体突然侧倾,相当于给悬架系统一个瞬时激励,使用0.1 rad阶跃信号来模拟,钟摆总长度L1+L2=0.45 m,改变悬架阻尼系数C2进行3组仿真,喷杆的阶跃响应曲线如图3所示,由于喷杆悬架装有粘滞阻尼器,作用在旋转轴P1的固有阻尼力占主导地位,在仿真过程中忽略了转轴处摩擦力。
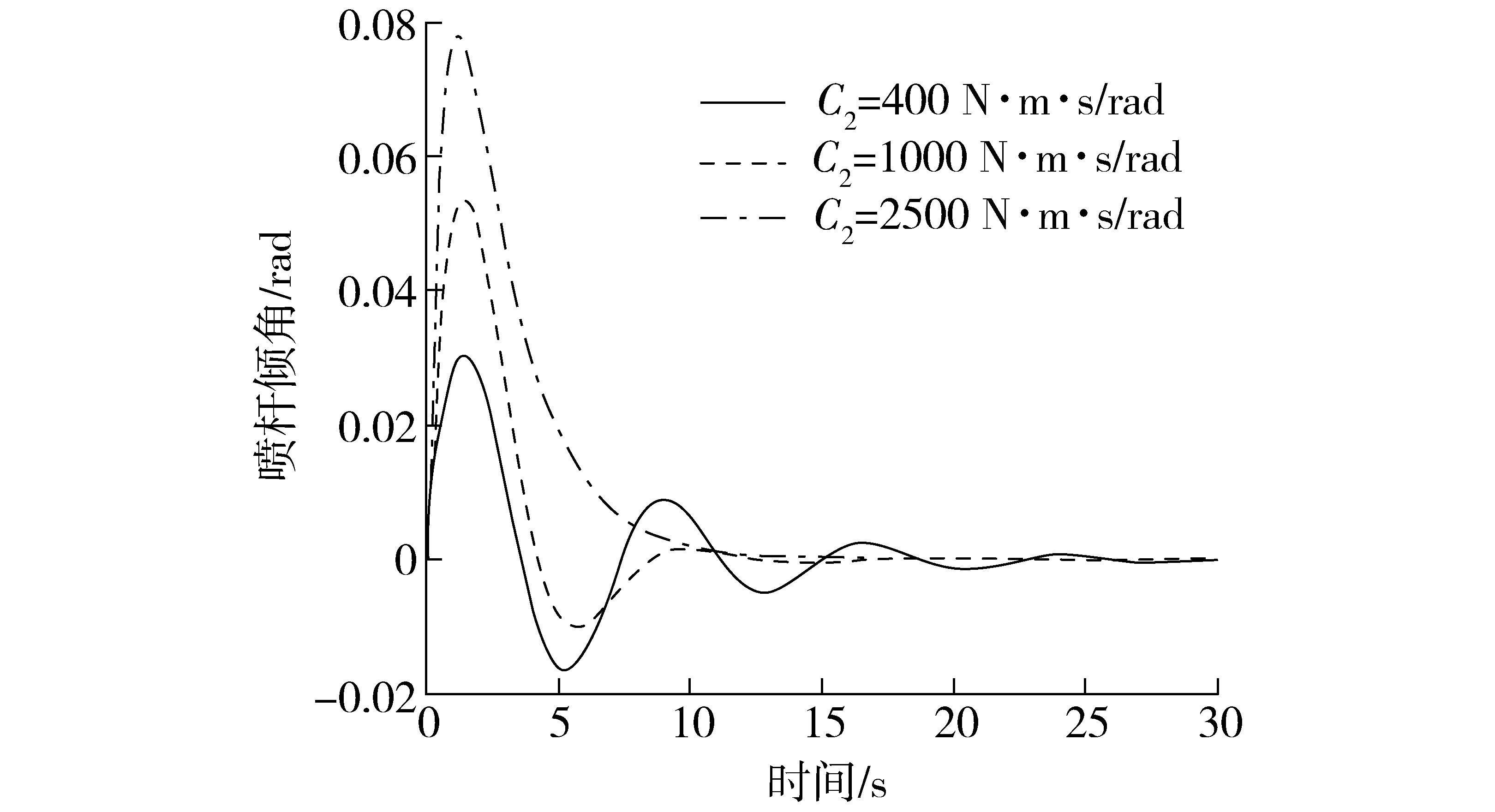
图3 不同阻尼系数被动悬架的阶跃响应Fig.3 Step response of passive suspension for different damping coefficients
3.2 钟摆转轴摩擦力影响分析
钟摆悬架受到的回复力矩近似等于Mg(L1+L2)sinφ,对于恒定的固有摩擦力矩F2,当L1+L2减小时,平衡摩擦力矩时,钟摆摆杆所处位置与重力方向的夹角φ变大。在φ变化范围±F2/[M2g(L1+L2)]内,回复力矩小于等于摩擦力矩时,喷杆可能回不到水平位置。库伦摩擦应尽量避免,悬架需要的阻尼应通过使用合适的粘滞阻尼器提供。如果两个摆长之和L1+L2太小,摩擦力F2的作用会阻止喷杆到达水平位置。如果L1+L2>0,转轴P1的摩擦F2为零时,喷杆平衡位置是水平位置,故无法适应地形变化,需要手动或者由自动控制系统控制喷杆跟踪地面坡度变化。
3.3 被动悬架频响特性优化

图4 被动悬架频率特性Fig.4 Frequency response functions of passive suspension
被动悬架的性能可以通过改变连杆长度L1、L2和阻尼系数C2来调整,通过被动悬架传递函数分析系统频率特性,图4为在不同阻尼系数下幅频特性曲线和相频特性曲线,从图中可以看出幅值比先增大后减小,钟摆悬架无法使喷杆完全隔离喷雾机扰动激励,当激励的频率超过悬架ωn,由式(5)被动悬架传递函数可得,喷杆倾角与车体倾角的幅值比趋向于式(19)的极限值。因此被动悬架的优化设计目标之一是幅值比最小化。
(19)
O’SULLIVAN[19]认为被动悬架应在6 s内将喷杆瞬态响应幅值衰减到初始值的10%以内;幅频特性曲线中,频率大于5 rad/s时,喷杆翻滚角与车体翻滚角的幅值比应小于0.2(-14 dB)。以上述两点为约束条件,以式(19)中频率响应的幅值比绝对值最小化为目标,在Simulink Response Optimization响应优化模块中,使用梯度下降法对钟摆总长度L1+L2和阻尼系数C2进行优化。优化后被动悬架阻尼系数C2=1 120.36 N·m·s/rad,摆长L1+L2=0.468 m,优化后系统的阶跃特性和频响特性如图5所示。

图5 优化后的阶跃响应和频响特性Fig.5 Optimization of step response and frequency response characteristics

图6 被动悬架有阻尼固有频率Fig.6 Damped natural frequency of passive suspension
3.4 含阻尼固有频率影响因素分析
通过数学模型分析摆长、阻尼及喷杆转动惯量对悬架有阻尼固有频率的影响规律,根据式(8)可知悬架的无阻尼固有频率与喷杆的质量、转动惯量及摆长有关,阻尼固有频率还与系统阻尼系数有关。绘制有阻尼固有频率响应曲面如图6所示,当悬架阻尼系数、喷杆转动惯量增大时,系统有阻尼固有频率随之减小;当摆长增大时,系统有阻尼固有频率随之增大。
4 基于比例控制的主动悬架动态响应分析
4.1 主动悬架比例控制
主动悬架由动力源、液压执行器、超声波距离传感器、信号处理、反馈和放大元件、悬架机构等组成。两个距离传感器时刻监测喷杆末梢与地面的高度,由高度差换算得到喷杆相对地面的倾角。通过模数转换、滤波处理后,由控制器发出控制信号,比例换向阀控制液压缸的流量和方向,液压缸以给定的速度动作,从而实现喷杆角度实时跟踪地形变化。大多数喷杆使用电液比例控制,四通阀控液压缸作为动力控制元件,假设不考虑油液的压缩性,驱动功率足够大可以保证油缸正常运动,这种情况下,液压缸位移xP与阀位移xV的传递函数可以简化为
(20)
式中KP——液压缸位移对阀位移的增益
控制器输出xV(阀位移)与超声波传感器检测到的偏差信号(γ-β)之间的关系,即控制器的传递函数为
(21)
四通阀通电后,由于液压系统的惯性,液压缸输出要滞后一段时间才接近所要求的输出值,所以控制律采用关系环节表示,T为时间常数,KV为阀的增益系数,从式(20)、(21)可以得出油缸伸缩量ΔP与偏差信号(γ-β)之间的传递函数为
(22)
基于比例控制的主、被动悬架Simulink仿真模型如图7所示,控制器即式(22)描述的数学关系,将式(15)~(18)描述的系统动力学方程组建立子系统(图中悬架动力学模型),系统有3个输入、1个输出,在已知α、φ、γ的情况下,通过Runge-Kutta算法求出喷杆倾角β的数值解。
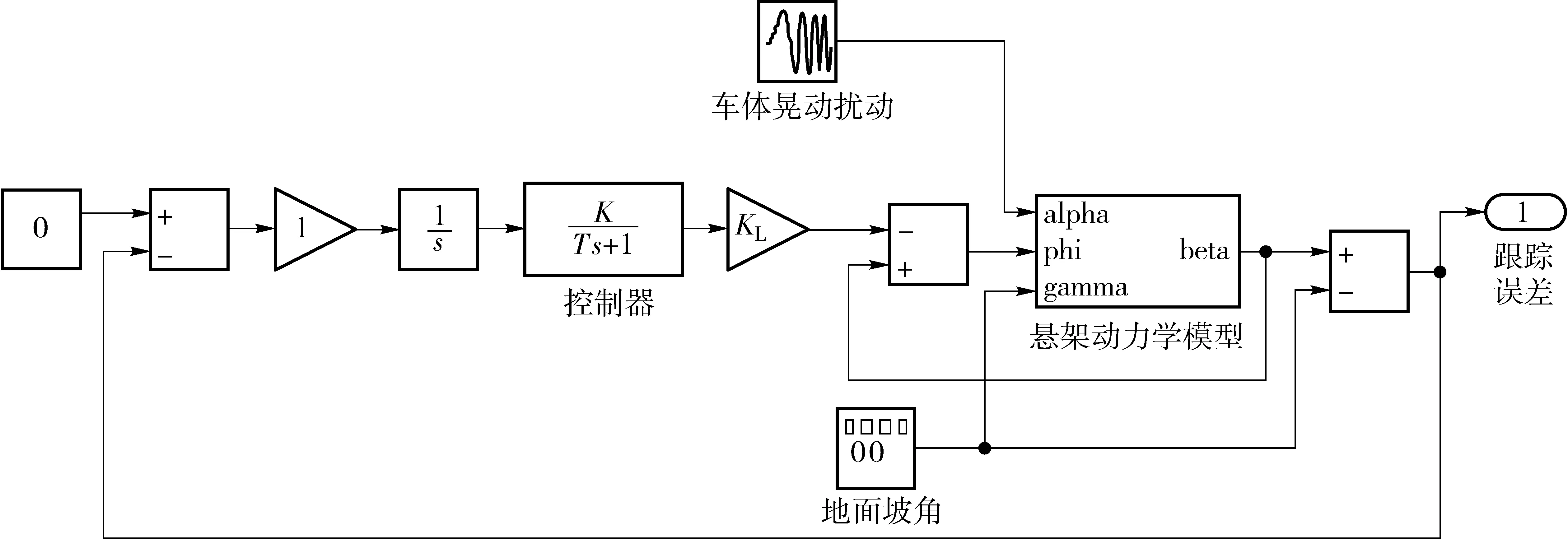
图7 基于比例控制的主动悬架仿真模型Fig.7 Simulation model of active suspension based on proportional control
喷杆悬架系统的理想频响特性:在小于指定频率(例如0.6 rad/s)时,幅值比应等于1(0 dB),即喷杆倾角β跟踪地面坡度γ变化,保持与地面平行,高于这个频率时幅值比应迅速降至0(-∞ dB)[19]。以地面坡度γ为输入,喷杆水平倾角β为输出,在Simulink中进行频率响应特性分析,如图8中实线所示。在较低的激励频率段,主动悬架幅值比在0 dB附近。随着激励频率逐渐增加,在0.29 rad/s处幅值最小为-1.306 dB,频率增大到0.738 rad/s时,幅值增大到最大5.27 dB,相当于对输入激励放大1.83倍,频率大于0.738 rad/s以后幅值迅速减小。可见比例控制器只能部分实现理想频响特性。若以车体侧倾角α为输入,以喷杆水平倾角β为输出,可得悬架被动部分的频响特性如图8中虚线所示,可知被动悬架不能跟踪低频的地面起伏波动,只能对底盘高频的运动干扰起到衰减作用。

图8 主动悬架、被动悬架频响特性Fig.8 Frequency response functions for active suspension and passive suspension
4.2 控制系统参数对响应特性的影响分析
从主动悬架数学模型可知决定主动悬架性能的参数是增益系数K、时间常数T、钟摆机构杆长L1、L2、L6以及喷杆质量M2和转动惯量I2。
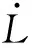

图9 控制器频响特性(K=0.22 m/(s·rad),T=0.4 s)Fig.9 Frequency response function of controller
当第1级钟摆摆长L1=0.35 m,第2级钟摆摆长L2=0.1 m,控制系统时间常数T=0.4 s,阻尼率ζ=0.5,不同增益K时系统的喷杆倾角β与地面坡度角γ频响特性如图10所示,系统跟踪误差β-γ与地面坡度角γ频响特性如图11所示。K从0增大到0.5,低频段的跟踪误差逐渐减小。随着频率增加,β-γ与γ幅值在共振频率处达到最大,K=0.5 m/(s·rad)系统的幅值比最大,频率大于共振频率后,幅值比都迅速衰减到零,无法对目标信号进行跟踪。

图10 不同增益K时主动悬架的频响特性Fig.10 Frequency response characteristics of active suspension with different gain K

图11 不同增益K时跟踪误差的频响特性Fig.11 Frequency response characteristics of tracking error of different gain K

图12 不同增益K时主动悬架阶跃响应Fig.12 Step response of active suspension with different gain K
改变比例增益系数K,系统输入量(地面坡度角γ)为阶跃信号时,喷杆倾角β的响应如图12所示,系统参数L1=0.35 m,L2=0.1 m,T=0.4 s,ζ=0.5,为了排除车辆翻滚运动的影响,凸显主动悬架作用下喷杆的响应,假设喷雾机翻滚角α=0。当增益值K大于0.5时,系统变得不稳定。
当L1=0.35 m,L2=0.1 m,T=0.4 s,ζ=0.5,K=0.22,α=0,改变控制系统的时间常数T,结果如图13所示,时间常数T从0.4 s减小到0.1 s时,悬架的性能没有显著提升,但是当时间常数增加到1 s时,跟踪误差被放大3.2倍,控制系统明显失控。
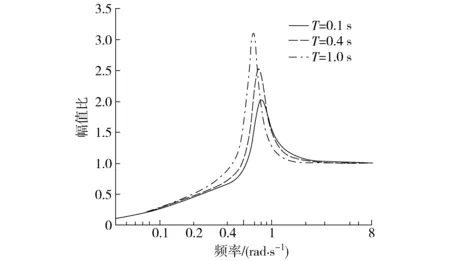
图13 不同时间常数T 时跟踪误差幅频特性Fig.13 Amplitude frequency characteristics of tracking error for different T
4.3 悬架结构参数对响应特性的影响分析


图14 不同摆长比L1/L2时主动悬架幅频特性Fig.14 Amplitude frequency characteristics of active suspension with different rod length ratios
当T=0.4 s,K=0.22 m/(s·rad),ζ=0.5,由式(7)可知,改变摆长L1+L2时,悬架系统的固有频率ωn随之改变,系统频响特性如图15。摆长之和变化时L2/L1保持恒定,使喷杆倾角产生相同变化量需要执行器伸缩量一致。随着L1+L2增加,共振频率处的幅值比增加,发生于低频段(0.83 rad/s以下)的幅值比却稍有降低。当激励频率大于0.83 rad/s时,L1+L2=0.6 m时的幅值比几乎是L1+L2=0.3 m的3倍,摆长越大,共振频率处的增益越大。频率大于共振频率时,被动悬架起主导作用,系统幅值比都迅速衰减,主动悬架的作用基本可以忽略。
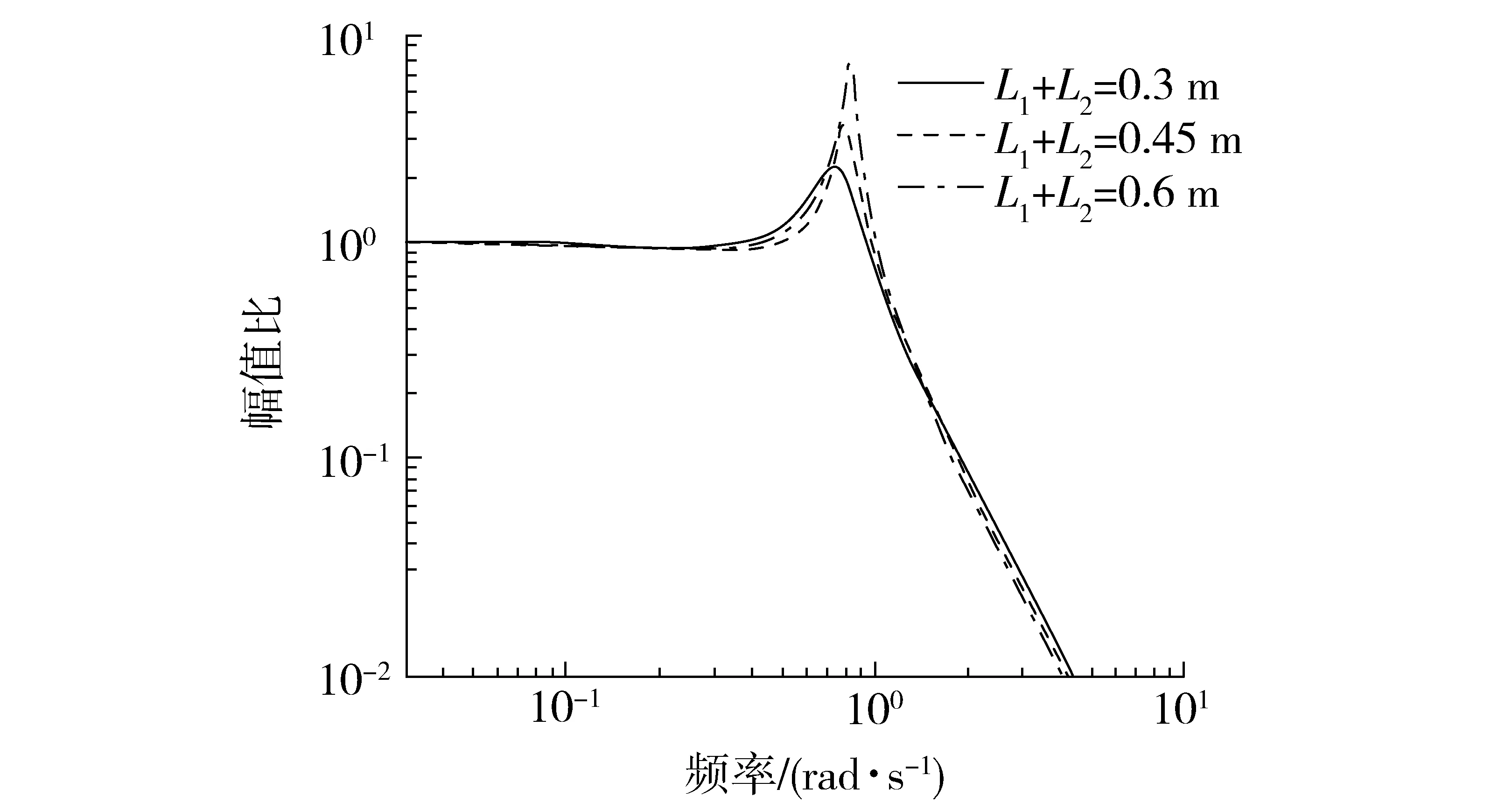
图15 不同摆长L1+L2时系统幅频特性Fig.15 Amplitude frequency characteristics for different length L1+L2
图16 阶跃响应γ=0.2 rad时液压缸作动功率变化曲线Fig.16 Changing curve of hydraulic cylinder power under step response γ=0.2 rad
5 试验
为了验证数学模型,以图17所示的28 m大型喷杆及其钟摆悬架为试验对象,进行动态响应测试,悬架钟摆总长度0.98 m。阻尼器选用分体式液压阻尼器,无复位弹簧,通过机电式万能试验机测试阻尼缸伸缩速度与力的关系,然后折算到转轴的阻尼系数为12 461 N·m·s/rad。喷杆浮动部分的质量通过起重行车上的电子秤测得922.6 kg。利用SolidWorks三维模型,测得喷杆绕质心Y轴方向惯量I2=32 700 kg·m2。
通过Stewart六自由度运动模拟平台进行喷杆运动试验,六自由度平台侧倾角运动范围±15°,频率0.01~35 Hz,以动平台的侧倾运动模拟喷雾机通过不平路面时车体的扰动α,喷杆及悬架安装于动平台上,喷杆的水平倾角β通过高精度IMU惯性测试单元(LORD Micro Strain 3DM-GX4-45)及东华测试DH5902动态采集系统测得。

图17 喷杆悬架系统动态特性试验平台Fig.17 Dynamic characteristic test platform of spray suspension1.控制台 2.运动模拟平台 3.喷杆及钟摆悬架 4.传感器与测试系统
通过六自由度运动平台产生绕Y轴的0.1 rad瞬态激励,喷杆倾角β响应如图18所示,试验曲线比模型预测稍有滞后,主要是由于转动副存在摩擦造成。
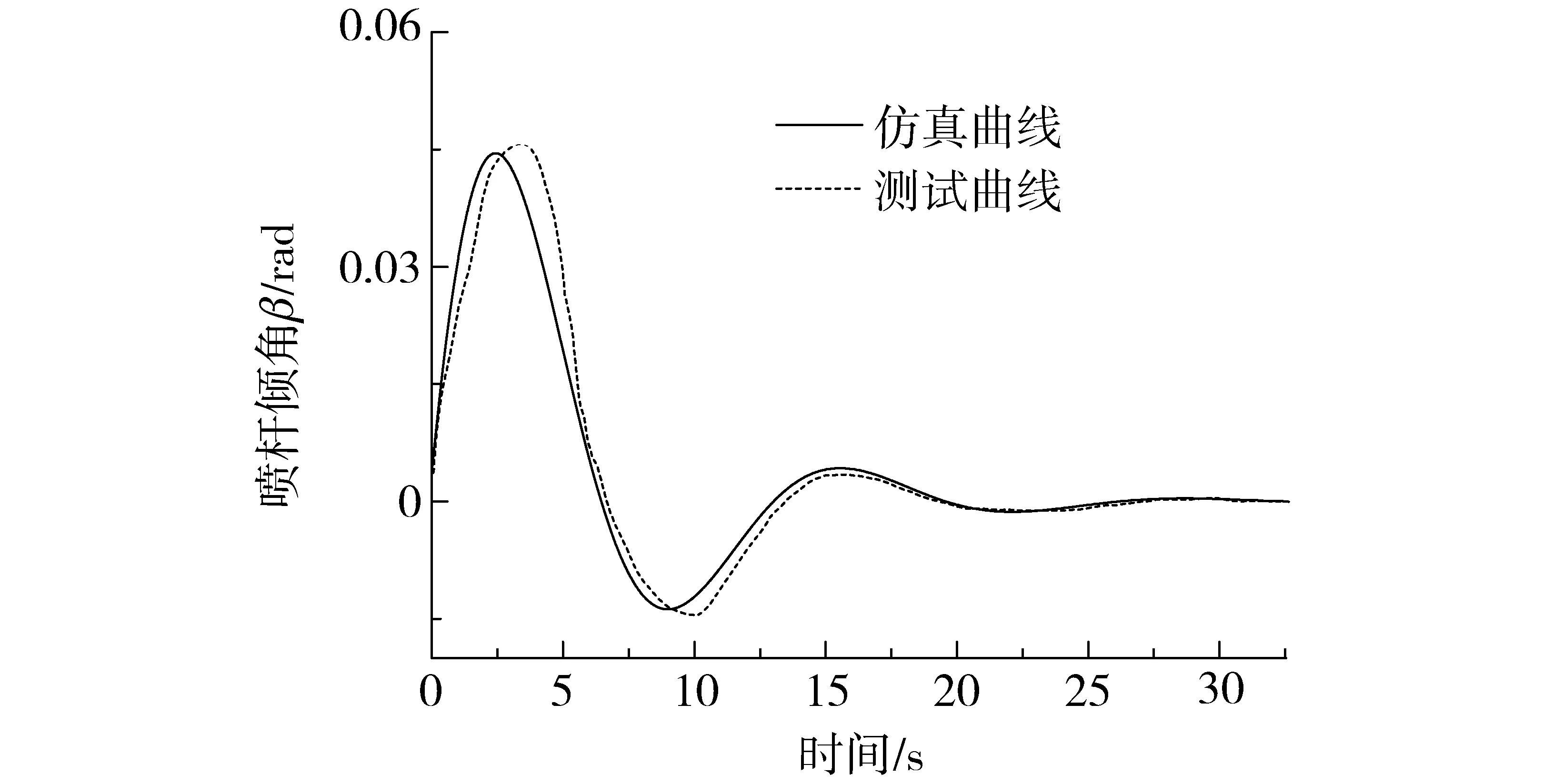
图18 被动悬架瞬态响应Fig.18 Step response of passive suspension
利用六自由度平台进行频响分析,使动平台输出绕Y轴转角正弦激励(幅值0.1 rad),激励频率在0.1~40 rad/s内取20个频率点,依次进行试验,记录喷杆达到稳态后的倾角幅值,频率响应曲线如图19所示。其中试验值与对应预测值的均方根误差为0.087,结果表明模型预测与试验数据吻合较好,数学模型可以用于喷杆动力特性的预测。
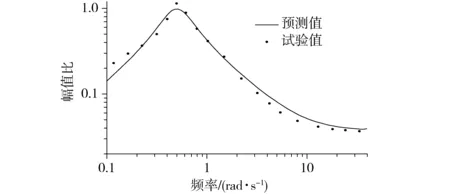
图19 钟摆悬架频率响应曲线Fig.19 Pendulum suspension frequency response curve
6 结论
(1)通过数学模型预测了喷杆的动力学特性,揭示了各悬架结构参数、控制参数对喷杆响应特性的影响机理,可指导参数科学配置。首先对被动悬架性能进行了分析,被动悬架能够衰减高于固有频率的激励,但不能使喷杆跟踪倾斜的地面,增设执行器可使喷杆跟踪地面坡度变化,提升被动悬架的性能。悬架有阻尼固有频率取决于摆长,较小程度上,取决于阻尼元件。
(2)基于建立的车体-悬架-喷杆系统动力学模型进行比例控制仿真研究,揭示了比例系数和时间常量对控制系统响应特性的影响规律,以及如何选择合适的比例系数和时间常量、摆长比等,使喷杆跟踪低频地面坡度起伏,削弱车体高频振动的影响。
(3)利用喷杆悬架系统动态特性试验平台,对某28 m喷杆及其被动悬架进行了瞬态响应测试和频响测试,试验点与数学模型预测值的均方根误差为0.087,下一步研究将根据模型分析结果,试制主动悬架的电液比例控制系统,对主动悬架数学模型预测的各种响应特性进行验证。
1 贾卫东,张磊江,燕明德,等.喷杆喷雾机研究现状及发展趋势[J].中国农机化学报,2013,34(4):19-22. JIA Weidong,ZHANG Leijiang,YAN Mingde,et al.Current situation and development trend of boom sprayer[J].Journal of Agricultural Mechanization Research,2013,34(4):19-22.(in Chinese)
2 邱白晶,何耀杰,盛云辉,等.喷雾机喷杆有限元模态分析与结构优化[J/OL].农业机械学报,2014,45(8):112-116,105. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20140818&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2014.08.018. QIU Baijing, HE Yaojie, SHENG Yunhui, et al. Finite element modal analysis and structure optimization of spray boom[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2014,45(8):112-116,105. (in Chinese)
3 RAMON H, MISSOTTEN B, DEBAERDEMAEKER J. Spray boom motions and spray distribution, partⅡ: experimental validation of the mathematical relation and simulation results [J]. Journal of Agricultural Engineering Research, 1997, 66(1): 31-39.
6 KENNES P, RAMON H, BAERDEMAEKER J D. Modelling the effect of passive vertical suspensions on the dynamic behavior of sprayer booms[J]. Journal of Agricultural Engineering Research, 1999, 72(3):217-229.
7 吴吉麟,苗玉彬. 不同激励源下宽幅喷雾机喷杆的动态特性分析[J]. 农业工程学报,2012,28(4):39-44. WU Jilin , MIAO Yubin. Dynamic characteristic analysis of boom for wide sprayer with different exciting sources[J]. Transactions of the CSAE,2012,28(4):39-44. (in Chinese)
8 陈达,陈志,周丽萍,等. 喷杆喷雾机等腰梯形悬架改进与验证[J]. 农机化研究,2014,36(4):171-174,178. CHEN Da,CHEN Zhi,ZHOU Liping, et al.Optimization design on boom suspension boom[J].Journal of Agricultural Mechanization Research,2014,36(4):171-174,178.(in Chinese)
9 陈树人,韩红阳,陈刚,等.喷杆喷雾机机架动态特性分析与减振设计[J/OL].农业机械学报,2013,44(4):50-53,20. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20130409&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2013.04.009. CHEN Shuren, HAN Hongyang, CHEN Gang, et al. Dynamic characteristic analysis and vibration reduction design for sprayer frame[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2013,44(4):50-53,20. (in Chinese)
10 FROST A R, O'SULLIVAN J A. Verification and use of a mathematical model of an active twin link boom suspension [J]. Journal of Agricultural Engineering Research, 1988, 40(4):259-274.
11 MARCHANT J A, FROST A R. Simulation of the performance of state feedback controllers for an active spray boom suspension[J]. Journal of Agricultural Engineering Research, 1989, 43(43):77-91.
12 DEPREZ K, ANTHONIS J, RAMON H, et al. Development of a Slow active suspension for stabilizing the roll of spray booms, part 1: hybrid modelling [J]. Biosystems Engineering, 2002, 81(2): 185-191.
13 DEPREZ K, ANTHONIS J, RAMON H, et al. PM-Power and machinery: development of a slow active suspension for stabilizing the roll of spray booms, part 2: controller design[J]. Biosystems Engineering, 2002, 81(3):273-279.
14 TAHMASEBI M, RAHMAN R A, MAILAH M, et al. Roll movement control of a spray boom structure using active force control with artificial neural network strategy[J]. Journal of Low Frequency Noise, Vibration & Active Control, 2013, 32(3):189-202.
15 TAHMASEBI M, RAHMAN R A, MAILAH M, et al. Active force control applied to spray boom structure[J]. Applied Mechanics & Materials, 2013, 315:616-620.
16 王松林,赵春江,王秀. 喷杆高度调节系统设计与试验[J].农机化研究,2014(8): 161-164. WANG Songlin,ZHAO Chunjiang,WANG Xiu. Design and experiments on boom height adjusting system[J].Journal of Agricultural Mechanization Research,2014(8): 161-164.(in Chinese)
17 陈文坊, 邱白晶, 杨宁,等. 基于超声波传感器的喷杆位姿控制系统[J]. 农机化研究, 2013,35(3):84-87. CHEN Wenfang,QIU Baijing,YANG Ning,et al.Spray boom position control system based on ultrasonic sensors[J].Journal of Agricultural Mechanization Research,2013,35(3):84-87.(in Chinese)
18 魏新华,邵菁,缪丹丹,等.喷杆式喷雾机喷杆高度及平衡在线调控系统[J/OL].农业机械学报,2015,46(8):66-71. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150811&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2015.08.011. WEI Xinhua, SHAO Jing, MIAO Dandan, et al. Online control system of spray boom height and balance[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2015,46(8):66-71. (in Chinese)
19 O’SULLIVAN J A. Verification of passive and active versions of a mathematical model of a pendulum spray boom suspension [J]. Journal of Agricultural Engineering Research, 1988, 40(2):89-101.
20 ANTHONIS J, AUDENAERT J, RAMON H. Design optimization for the vertical suspension of a crop sprayer boom [J]. Biosystems Engineering, 2005, 90(2): 153-160.
Modeling and Simulation of Dynamic Behavior of Large Spray Boom with Active and Passive Pendulum Suspension
CUI Longfei1,2XUE Xinyu1DING Suming1GU Wei1CHEN Chen1LE Feixiang1
(1.NanjingResearchInstituteforAgriculturalMechanization,MinistryofAgriculture,Nanjing210014,China2.KeyLaboratoryofModernAgriculturalEquipmentandTechnology,MinistryofEducation,JiangsuUniversity,Zhenjiang212013,China)
When sprayer works in the field, boom movement seriously affected the spray distribution, suspension system is the key device to control the dynamic behavior of boom. The response of a boom suspension should be such that it isolates the boom from high frequency roll of vehicle as it travels over bumpy ground, while transmitting low frequency roll so that the boom can follow undulating and sloping ground. In order to solve the dynamics and control problems of double pendulum active and passive suspension mechanism, considering the coupling effect of vehicle body motion, change of terrain slope, friction of moving pair, etc., a higher order differential equation group was established to describe the dynamic behavior of boom by using the second kinds of Lagrange dynamics equation. Based on this, the dynamic characteristics of the passive suspension were studied, and the effects of these factors, such as damping, friction and pendulum length on the response characteristics were analyzed. A Matlab/Simulink simulation model of active suspension based on hydraulic proportional control was established, and then the influence of gain coefficient, time constant and suspension structure parameters on the boom response and tracking error was revealed. By using Stewart six degree of freedom motion simulation platform and dynamic testing system, step response test and frequency response test were conducted on a spray boom with pendulum suspension, the root mean square error between frequency response test value and the mathematical model predictive value was 0.087. It was demonstrated that the model could be used in the design of a suspension to give a specified response to the rolling motion of the spray vehicle,and the results showed that the model can be used to predict the dynamic response characteristics of the boom, and guide the design of large boom suspension.
boom sprayer; suspension; dynamic analysis; simulation; experiment
10.6041/j.issn.1000-1298.2017.02.011
2016-05-19
2016-07-28
国家自然科学基金项目(51605236)、国家重点研发计划项目(2016YFD0200700)和江苏省农业科技自主创新资金项目 (CX(16)1043)
崔龙飞(1989—),男,助理研究员,江苏大学博士生,主要从事机械系统动力学研究,E-mail: cuilong.fei@163.com
薛新宇(1969—),女,研究员,博士生导师,主要从事植保机械技术研究,E-mail: 735178312@qq.com
S49
A
1000-1298(2017)02-0082-09
