基于PPCA消噪和谱峭度的滚动轴承故障诊断方法

朱德程，向家伟

(温州大学机电工程学院，浙江温州 325035)

基于PPCA消噪和谱峭度的滚动轴承故障诊断方法

朱德程，向家伟†

(温州大学机电工程学院，浙江温州 325035)

基于概率主成分分析（Probabilistic Principal Component Analysis，PPCA）和谱峭度方法，提出一种轴承故障诊断新方法．用主元模型对原始信号进行消噪，可完整地保留信号的有用成分，并能大幅度提高信噪比，解决故障信号易受噪声干扰的问题．对消噪后的信号进行基于谱峭度的最优带通滤波和包络谱分析，由包络频谱诊断轴承故障．通过数值仿真和实验验证了所给方法的正确性和有效性．所给方法可用于滚动轴承的故障诊断．

概率主元分析；谱峭度；滚动轴承；故障诊断

当轴承发生故障时，处于不同周向分布角的滚动体经过故障位置处就会产生周期性冲击载荷，其振动信号在轴承固有频率附近会出现均匀的调制边频带，然而，直接采用频谱分析无法识别出这种由故障信号调制的高频载波非等周期冲击信号，目前采用的最有效方法是包络分析法，而包络分析法的效果取决于对振动信号进行预处理和去噪处理法的优劣．文献[1]用AR模型对原始信号进行滤波，滤除稳定成分以增强故障冲击成分，但对于冲击持续时间很短的短数据，由AR参数得出的谱估计的分辨率会很差，并且Morlet小波波形参数是常数，小波与冲击成分的匹配性差，影响包络结果．文献[2]通过求理想故障信号相对于实测带噪信号的后验概率密度的期望的方式，给出原始信号的最小均方差估计，进行消噪．该方法虽然考虑了有、无故障冲击的概率，但当采样数据不够长、先验信息不准时，不能保证噪声估计结果的正定性．文献[3]使用经验模式分解（EMD）将原始信号分解为不同尺度的本征模式分量（IMF），通过选取峭度值大于3的IMF重构信号，达到降噪目的．EMD消噪法突出了信号的高频共振成分，能提高峭度值，但存在模态混叠问题，无法将高频噪声分离出去，得到的高频分量通常被当作噪声直接去除，这样就有可能舍掉了有用的信号成分．谱峭度的包络分析方法[4]主要用于轴承早期故障微弱信号的诊断，其对瞬态冲击信号敏感，并能明确指出确定瞬态成分所在频带，但易受噪声干扰，不适合强噪声环境下的状态检测．本文提出了一种基于 PPCA消噪和谱峭度的滚动轴承故障诊断方法，并运用Hilbert包络计算，由包络频谱诊断轴承的故障特征．实验表明，所给方法能较为完整地保留有用信号成分，有效抑制噪声，提高故障诊断的准确性．

1 概率主元（PPCA）消噪与谱峭度法

1.1 概率主元模型

概率主元模型[5-8]是在因子分析法隐含变量模型的基础上，假设高斯噪声的方差各向同性，由因子向量（主元向量）叠加噪声产生的生成模型，数学形式为：

其中，X为原始变量，是m× n阶经归一化处理的采样数据，m为采样数，n为原始变量个数；P为待求的m×k阶负荷向量，k为主元个数，且k＜m；t为主元变量；e( t)为高斯噪声．

确定概率模型后，分别计算主元变量、原始变量在给定主元变量、主元变量在给定原始变量下的分布，获得PPCA模型．

原始变量在给定主元变量下的条件分布为：

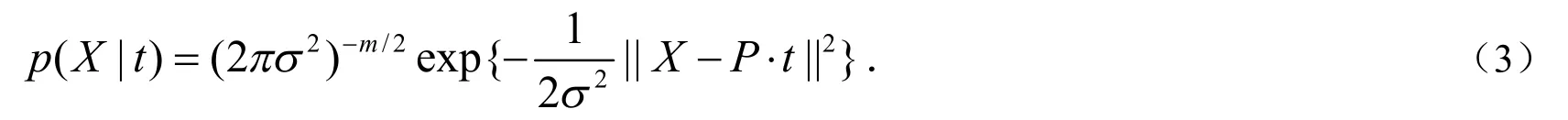
原始变量的分布为：

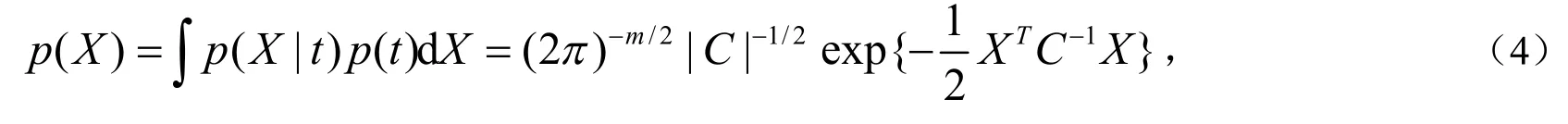
1.2 概率主元消噪方法

根据 1.1得到的负荷向量P，将归一化处理的原始数据X分解为P的外积之和，得到原始数据的主元模型，其数学表示为：

1.3 谱峭度法与带通滤波频率

峭度对冲击信号敏感，常用来检测含噪信号中的瞬态成分，但由于峭度值易受噪声干扰，为此提出了谱峭度方法，该方法既能检测瞬态冲击成分，又能确定频率的峭度值．定义信号X( t)的的系统激励响应Y( t)的谱形式为：

其中，E{·}表示求期望，|·|表示求模．

由式（13）可知，SK值由信号的系统响应传递函数决定，所以与滤波器的中心频率和带宽的选择有关．当带宽趋于无限小，则SK值为0，当带宽很宽时，受噪声影响，SK将无法检测到窄带瞬态信号．因此，对于非平稳信号，SK值是中心频率和带宽的函数．所以，快速峭度图[12]的基本思想是：给定一组关于中心频率和带宽的数组，将每组参数作为带通滤波器参数对信号滤波，然后计算滤波后信号的包络，最后计算每一时域包络信号的峭度，与最大SK值对应的参数就是最优中心频率和带宽．

2 基于PPCA消噪和谱峭度的滚动轴承故障诊断方法

轴承早期的故障特征频率信号很微弱，进行采样包络分析时，截取的采样信号一般位于轴承共振频率附近，因为轴承的共振频率很高，如果不对采样信号作消噪处理，进行频率谱峭度计算时得到的中心频率就会和轴承共振频率相差很大，截取的信号有可能不能有效地包含轴承的故障特征成分．另外，噪声干扰强度过大，也会使频谱分析的分辨率变差。基于此，本文提出一种滚动轴承混合诊断方法，其诊断流程如图1所示．

首先采用PPCA对原始振动信号进行预处理，这样既能有效制止高斯噪声又不损失主要信息；然后由快速谱峭度图确定最优带通滤波器的中心频率和带宽，利用所得参数对消噪后信号作带通滤波，通过Hilbert法计算其包络，并作降采样处理；最后对比包络频谱和轴承故障频率诊断出轴承故障．

3 仿真与实验

3.1 仿真实验分析

为验证本文提出方法的正确性，以振动衰减信号、低频干扰信号和白噪声的组合作数字仿真，其表达式为：

式（14）中，用以描述轴承固有频率为4 000 Hz的振动衰减号为：

转频干扰信号为：

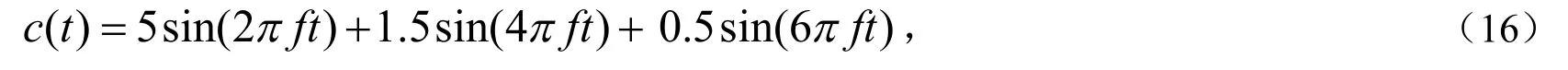
其中，f为安装轴承的轴转频，若取转速n=1 480r/min ，则f=n/60Hz．

设轴承故障冲击周期T = 0.01，即故障频率为100 Hz的周期性冲击振动，采样频率fs= 40 960 Hz，采样点数为4 096点．仿真信号的时域图及频谱图分别如图2、图3所示．

从仿真信号时域图（图2）看，信号中含有周期性冲击成分，但因为噪声干扰，很难确定冲击周期，频谱图（图3）中虽然能看到的故障轴承的中心频率在4 000 Hz附近，但由于噪声的混叠，无法准确定位，故障频率的调频带也不明显．为了抑制噪声，对原始信号作PPCA消噪处理，处理后的时域图和频谱图分别如图4、图5所示．比较图3和图5可知，消噪后谱图相（图5）对于未消噪的图3信号明显增强，并且在中心频率4 000 Hz附近出现均匀的调制频率为100 Hz的边频带，正好为轴承的故障特征频率．

对PPCA消噪信号计算SK，得到快速峭度图如图6所示，最大SK对应的中心频率为4 196 Hz，和共振频率4 000 Hz非常接近．带宽为640 Hz，最大峭度为6.4．

利用快速峭度图得到最优中心频率和带宽，对 PPCA消噪的信号进行带通滤波，结果如图7所示．由图7可见，时域图中振动冲击成分清楚地凸显出来，在0.1s中包含10个冲击．

对带通滤波后信号进行Hilbert包络计算．为提高频谱分析的分辨率，对包络计算结果作降采样处理，降采样率D = 50，得到包络频谱如图8所示．从图8能清晰地看到故障频率100 Hz及其倍频成分，和仿真的故障冲击频率完全吻合．

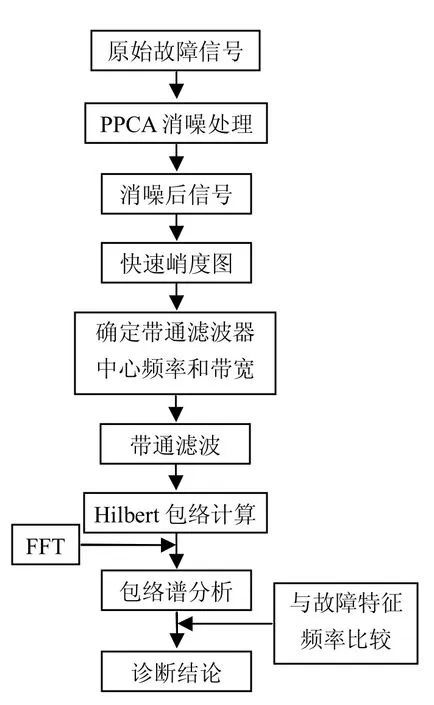
图1 故障诊断流程图

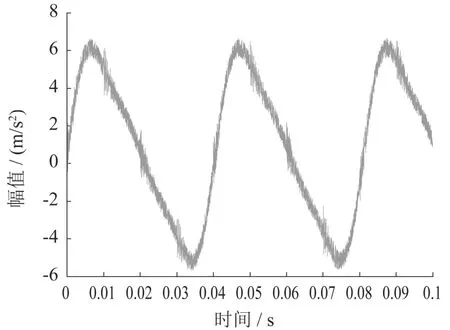
图2 仿真信号时域图

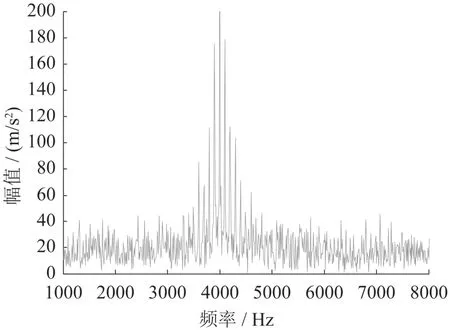
图3 仿真信号频谱图

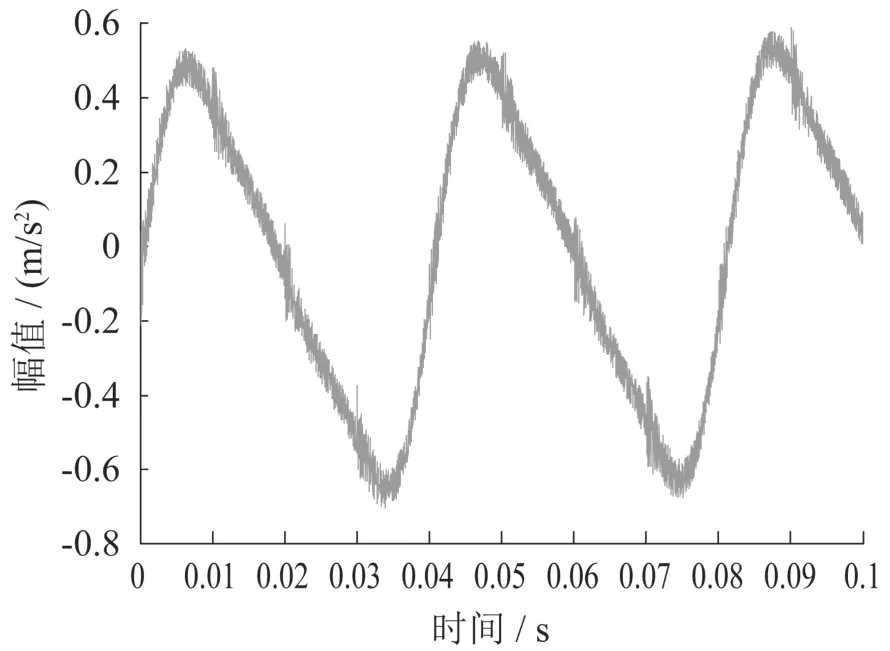
图4 PPCA消噪后时域图

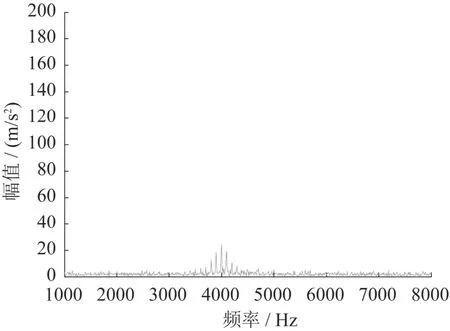
图5 PPCA消噪后频谱图

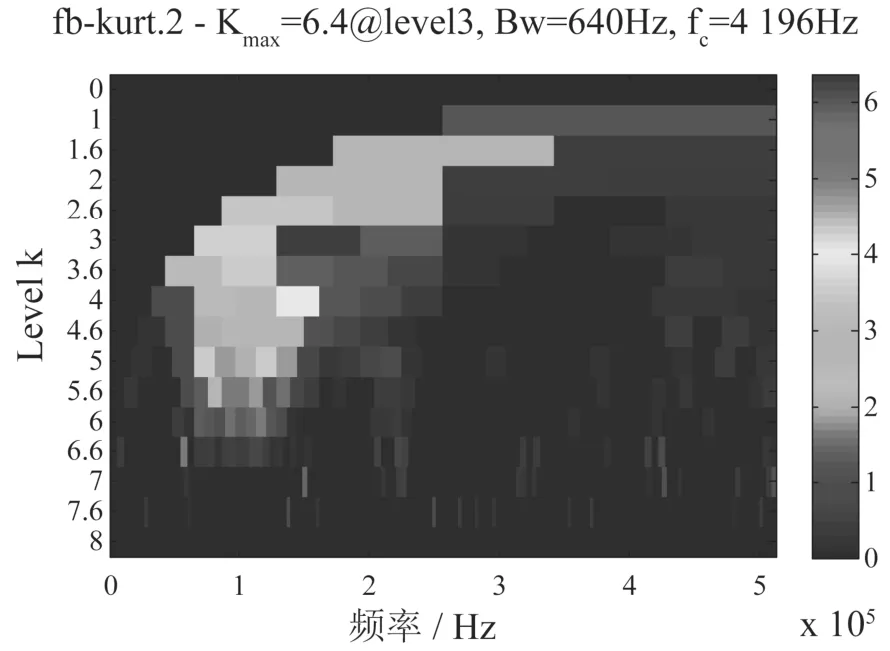
图6 PPCA消噪信号的快速峭度图

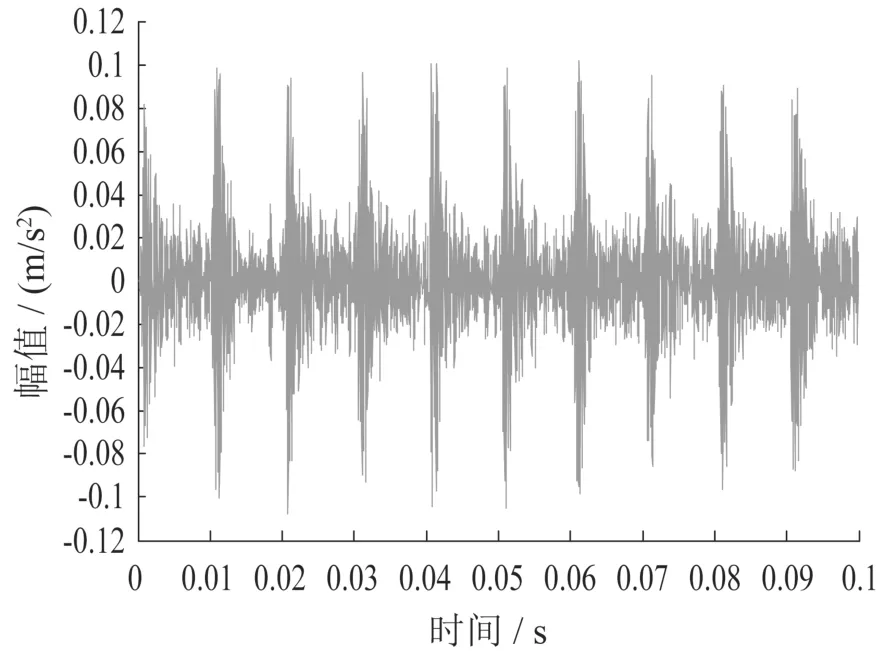
图7 PPCA消噪信号带通滤波后波形图

为验证PPCA消噪效果，直接对原始信号进行Hilbert包络分析，结果如图9所示．从图9可以看出，由于噪声信号的干扰使得故障频率及其倍频完全淹没在噪声中，无法解调出来．

以上对比分析表明，PPCA消噪能有效抑制噪声，凸显轴承中心频率及其周围的故障边频带，为快速峭度图准确选择最优滤波参数提供条件，从而准确地诊断出轴承的故障特征．

3.2 实验验证

以外圈故障轴承的故障诊断为例，对本文方法的可行性进行验证．实验测试平台采用美国Spectraquest公司生产的“机械故障综合模拟实验台（MFS-MG）”，如图10所示，主要结构包括转速显示器、手动调速器、位移传感器、测速传感器、电机、主轴等．

图8 包络频谱图

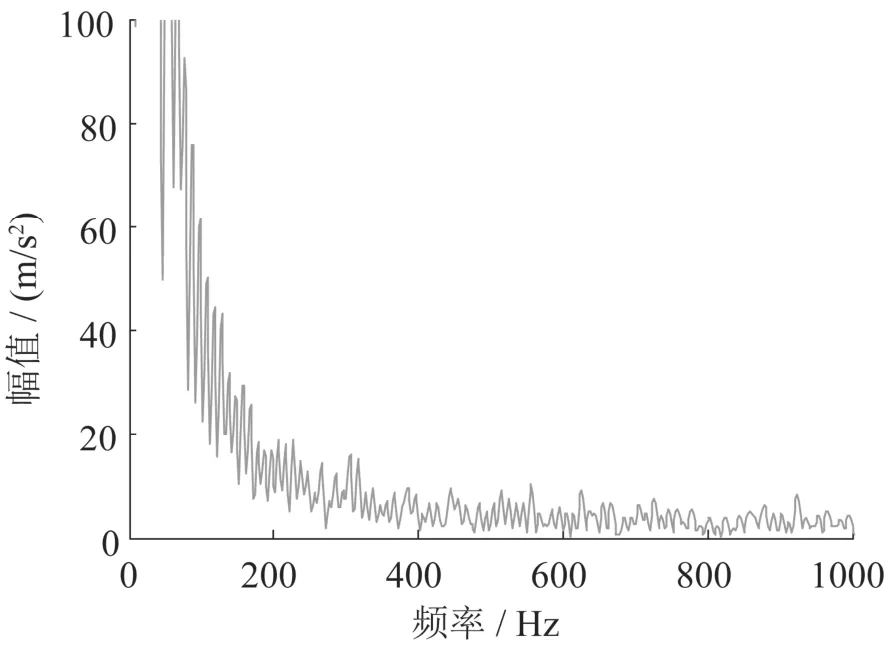
图9 原始信号直接包络解调频谱图

图10 MFS-MG机械故障综合模拟实验台

实验轴承型号为ER-12K，其参数：滚动体的个数为8，滚动体直径为7.937 5 mm，轴承的节圆直径为33.477 2 mm．

实验轴承空载运行，转速2 990 rpm，采样频率25.6 kHz，采样点数327 680，以靠近电机左端轴承座位置的传感器获取其振动信号，由传感器经数据采集卡后连接到计算机上运用VQ软件完成数据采集．由滚动轴承故障特征频率理论公式得到外圈故障特征频率为152.1 Hz．

原始数据的时域图如图 11所示，图中显示的冲击特性不明显．为提高信噪比，采用 PPCA去噪处理，结果如图12所示．

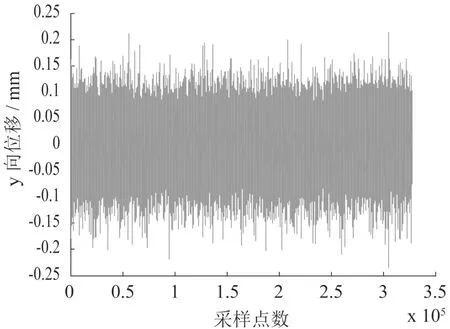
图11 原始信号波形图

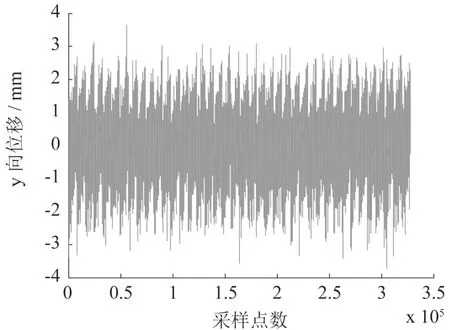
图12 PPCA消噪后信号波形图

对比图11和图12可知，抑制噪声后，冲击特性初步显现出来了（见图12）．对消噪信号，采用快速峭度图计算SK值（结果如图13所示），得到使信噪比最高的频带参数：中心频率为9 800 Hz，带宽为400 Hz，最大峭度值5.1，处于第5分解层，其它频带的信噪比都比较低．

对带通滤波信号进行Hilbert包络计算，并作降采样处理，降采样率D = 50，得到包络频谱图如图14所示．对不消噪信号直接进行包络计算得到的频谱图如图15所示．对比图14和图15可见，外圈的故障特征频率152 Hz能从PPCA消噪包络频谱图中清晰地解调出来，其与滚动轴承故障特征频率理论计算结果 152.1 Hz非常吻合，从而可诊断出轴承的外圈发生了故障．如果信号不作消噪预处理，则故障频率会被噪声完全湮没，无法提取特征频谱．

图14 PPCA消噪信号包络频谱图

图13 PPCA消噪信号快速峭度图

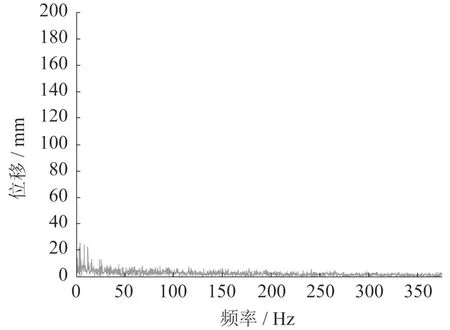
图15 不消噪信号包络频谱图

4 结 论

本文提出了基于PPCA消噪和谱峭度的滚动轴承故障诊断方法．利用PPCA消噪充分抑制了噪声和低频干扰，增强了中心频率及其周围的调制边频带，提高了信噪比，利用快速峭度图确定了带通滤波器的最优中心频率和带宽，最后对带通滤波后的信号进行Hilbert包络计算，根据轴承故障频率得出诊断结果．数值仿真和实验研究表明，PPCA消噪能有效地提高信噪比，抑制噪声，使轴承共振频率附近的故障频率调制现象凸显出来，是一种较好的诊断滚动轴承故障的方法．

[1] 郭瑜，郑华文，高艳等. 基于谱峭度的滚动轴承包络分析[J]. 振动、测试与诊断，2011，31（4）：517-521.

[2] 周智，朱永生，张优云，等. 基于MMSE和谱峭度的滚动轴承故障诊断方法[J]. 振动与冲击，2013，32（6）：73-77．

[3] 苏文胜，王奉涛，张志新，等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击，2010，29（3）：18-21．

[4] Sawalhi N,Randall R B,Endo H. The enhancement of fault detection and diagnosis in rolling element bearings usingminimum entropy deconvolution combined with spectral kurtosis [J]. Mechanical System and Signal Processing,2007,21: 2616-2633.

[5] Tipping M E,Bishop C M. Probabilistic principal component analysis [J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology),1999,61(3): 611-622.

[6] 杨沛武. 概率PCA多元统计方法在过程监控中的应用研究[D]. 无锡：江南大学自动化研究所，2008：16-20.

[7] 岳春柳. 缺失数据的概率主成分分析[D]. 长春：东北师范大学数学与统计学院，2010：9-14.

[8] 王井东. 线性与核高斯模型及其混合模型的研究[D]. 北京：清华大学电子工程系，2004：14-18.

[9] Dempster A P,Laird N M,Rubin D B. Maximum likelihood from incomplete data via the EM algorithm [J]. Journal of the Royal Statistical Society,B,1977,39(1): 1-38.

[10] Jordan M I,Jacobs R A. Hierarchical mixtures of experts and the EM algorithm [J]. Neural Computation,1994,6(2): 181-214.

[11] Ghahramani Z,Beal M J. Varitional inference for Bayesian mixtures of factor analyzers [J]. Proc NIPS,1999,12: 449-455.

[12] Antonia J,Randall R B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines [J]. Mechanical Systems and Signal Processing,2006,20(2): 308-331.

The Method of Rolling Bearing Fault Diagnosis Based on PPCA Noise Elimination and Spectral Kurtosis

ZHU Decheng,XIANG Jiawei
(College of Mechanic and Electronic Engineering,Wenzhou University,Wenzhou,China 325035)

Based on the method of probabilistic principal component analysis (PPCA) and spectral kurtosis method,a new fault diagnosis approach is proposed. The useful component of the signals is completely retained and the signal- to-noise ratio (SNR) is greatly improved by using the principal component models to de-noise original signal. The problem of the fault signals is susceptible to noise interference is solved effectively. The optimal band-pass filter using spectral kurtosis and envelope spectrum are employed to analyze the de-noised signal. Then the bearing faults are detected though the frequency information of envelop spectrum. Numerical simulation and experimental investigation verify that the present approach is corrective and effective and can be applied to the fault diagnosis of rolling bearings.

PPCA; Apectral Kurtosis; Rolling Bearing; Fault Diagnosis

TH133.33

：A

：1674-3563(2017)01-0047-08

10.3875/j.issn.1674-3563.2017.01.006 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2015-06-29

国家自然科学基金(51175097)；浙江自然科学杰出青年基金资助项目(LR13E050002)

朱德程(1990- )，男，山东齐河人，硕士研究生，研究方向：机械故障诊断．† 通讯作者，jwxiang@ wzu.edu.cn