基于ECM算法的混合改进威布尔分布的参数估计

刘小宁

(温州大学数学与信息科学学院，浙江温州 325035)

基于ECM算法的混合改进威布尔分布的参数估计

刘小宁

(温州大学数学与信息科学学院，浙江温州 325035)

混合改进威布尔分布是寿命数据分析中重要的统计模型，但是利用矩估计、极大似然估计等传统的统计方法来估计模型的参数比较困难．应用结合牛顿迭代法的 ECM 算法研究了混合改进威布尔分布在正常工作条件下的完全数据场合、截尾数据场合的参数估计问题，并得出了相应数据场合下各参数的极大似然估计．

混合改进威布尔分布；ECM算法；牛顿迭代法；完全数据；截尾数据

寿命数据分析已经成为工业、生命科学等多个领域研究的热点问题．在寿命可靠性分析中，经常会用到威布尔分布，一般形式为二参数威布尔分布，因其简单易解且具有优良的统计性质而被广泛使用．然而对于具有以损耗失效为特征的某些机械零部件，与二参数威布尔分布相比，采用三参数威布尔分布进行拟合和参数估计，可以得到更高的精度，更能反映产品可靠性的实际情况，也更具合理性．改进威布尔分布[1]（the New Modified Weibull Distribution）是一项有浴缸形故障率函数的新的寿命分布，被认为是另一有用的三参数威布尔分布的一般形式．对于单个总体寿命数据的分析，其统计方法已经非常成熟，但是在实际应用时经常会遇到混合分布的情况．大量事实表明，混合改进威布尔分布作为具有一个以上失效模式的单元的寿命分布模型是合适的，但是由于缺少混合改进威布尔分布的统计分析方法，这种模型没有得到广泛应用．目前国内外研究多是对三参数威布尔分布进行参数估计，往往是单个总体，如严晓东等[2]选择常用的5种三参数威布尔分布参数估计法进行比较研究，汤银才等[3]给出了三参数威布尔分布参数的贝叶斯估计．对于混合威布尔分布的参数估计研究，多数讨论的是混合二参数威布尔分布，如蒋卉等[4]利用ECM（Expectation Constraint Maximization）算法对混合二参数威布尔分布进行参数估计，取得了较好的成果．对于混合三参数威布尔分布的参数估计研究较少，张锡清[5]采用混合三参数威布尔分布来描述齿轮的可靠性，用极大似然法估计分布参数，并通过最优化方法求极大似然值，取得了正确结果．

基于ECM算法在多参数估计方面的优越性和混合改进威布尔分布的实用性，本文构造混合改进威布尔分布，利用ECM算法，在完全数据场合和截尾数据场合下，对参数进行估计．为了研究方便，本文仅考虑两个改进威布尔分布混合的情形．下面记NMWD（the New Modified Weibull Distribution）为新改进的威布尔分布．

1 ECM算法和牛顿迭代法

1.1 ECM算法

EM（Expectation Maximization）算法是近几年发展很快且应用很广的一种估计参数的方法，它是一种迭代方法，由Dempster等[6]提出，这种方法简化了极大似然估计的计算．当极大化无显式表示时，给出了广义EM算法，即GEM（General Expectation Maximization）算法．Meng等[7]提出了一种特殊的GEM算法，称之为ECM算法，该算法保留了EM算法的简单性和稳定性．

EM算法主要用来解决不完全数据情况下对未知参数进行极大似然估计的问题．假设Y是观测数据，Z是潜在数据，θ是未知参数，以表示θ的基于观测数据Y的后验分布密度函数．表示添加数据Z后得到的关于θ的后验分布密度函数，表示在给定θ和观测数据Y下潜在数据Z的条件分布密度函数．我们计算的目的是观测后验分布的众数．于是，EM算法可以如下进行，记θ（m）为第m+1次迭代开始时后验众数的估计值，则第m+1次迭代的两步为：

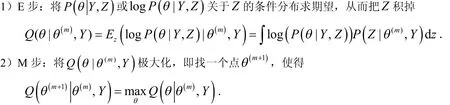
1.2 牛顿迭代法

牛顿迭代法又称为牛顿-拉夫逊方法，它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的算法．我们知道大量非线性方程不存在显示解，求精确根非常困难，甚至不可能，而牛顿迭代法是解非线性方程最著名和最有效的方法之一．所谓牛顿迭代法，其基本思想是将非线性方程转化为线性方程来求解．

设f（x）为一个连续可微的分布函数，f（x）在点x0的某领域内展开成泰勒级数．的情况下，取其线性部分，并令其等于0，即，以此作为非线性方程的近似方程．若，则其解为，这样，得到牛顿迭代法的一个迭代关系式

2 完全数据场合的参数估计

混合分布的参数估计用常规方法很难得到其极大似然估计，而用ECM算法可以很好地解决这一难题．下面我们用ECM算法来求混合改进威布尔分布在完全数据场合的参数估计．

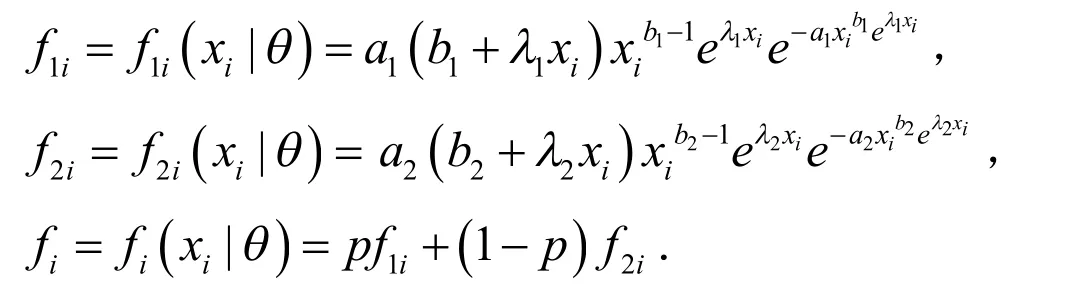
由于我们不知道Xi是来自 f1i还是来自 f2i的改进威布尔总体，因而Ii是不能被观测到的随机变量．Xi和Ii的联合分布为

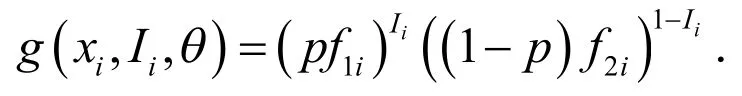
从而在Xi给定下，Ii的条件分布为：

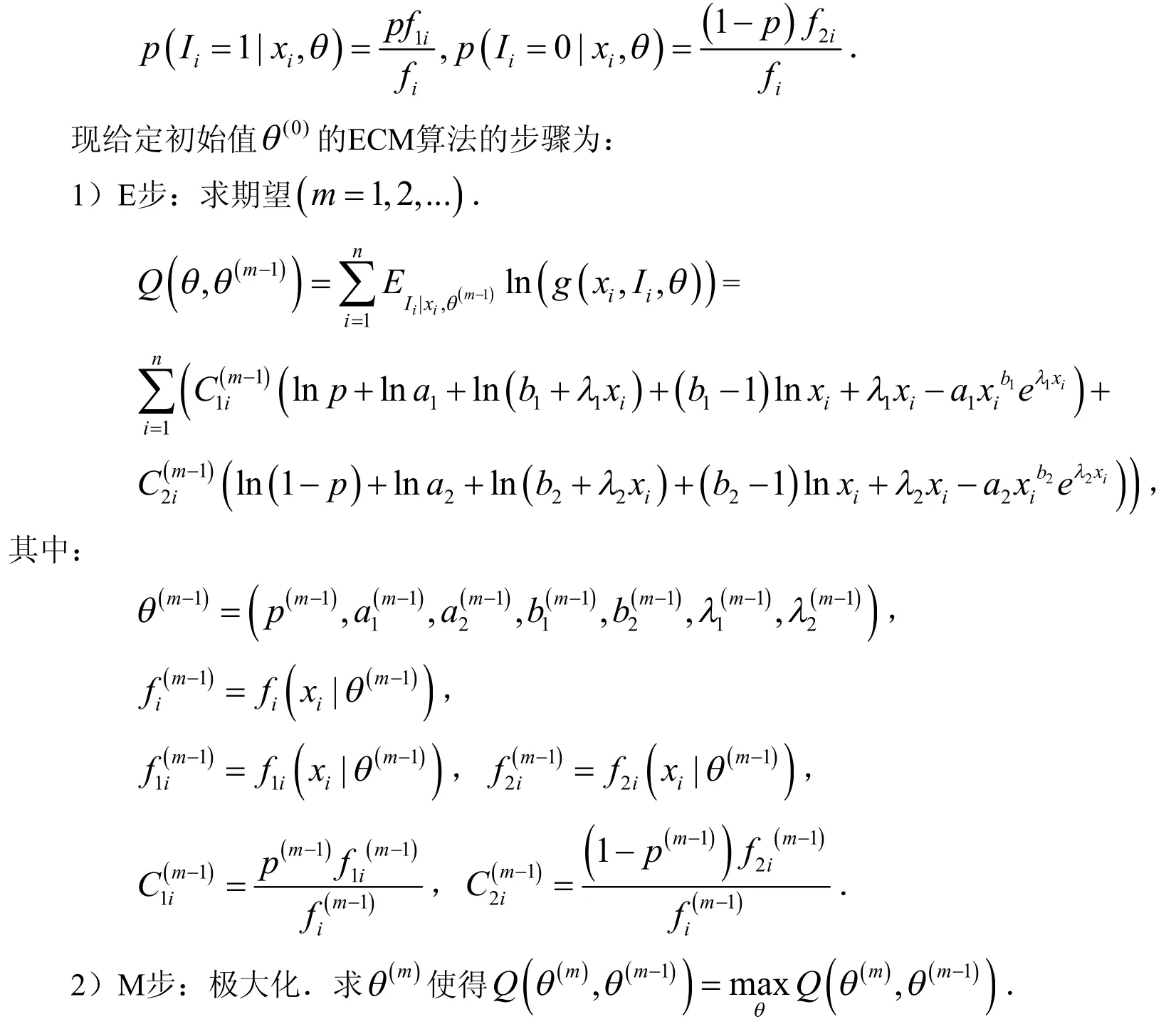
文中k=7，每一步条件极大化可按下面的方法求得．

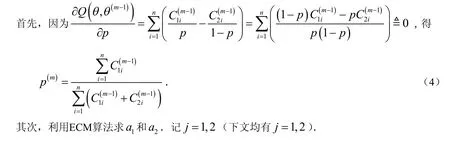
3 截尾数据场合的参数估计

3.1 定数截尾情形

如果观测到有r个产品失效则停止试验，观测时间为xr，则有(n-r)个产品未失效．记：

其中Sj ,j=1,2表示(n-r)个未失效产品的生存函数．对于没有截尾的样品， Xi和的联合分布为．在给定条件下，Ii的条件分布：

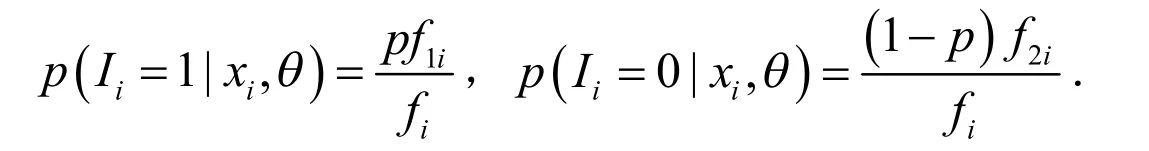
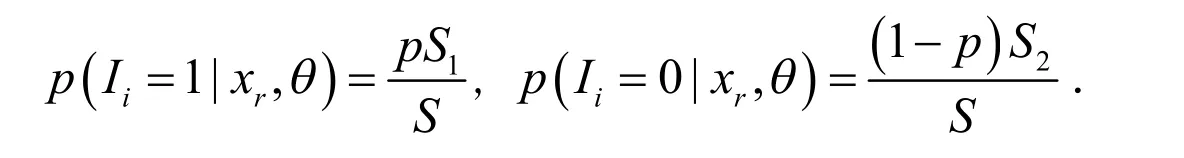
1）E步：求期望(m=1,2,...)．

3.2 定时截尾情形

如果寿命试验进行到时刻τ为止，有r个产品失效，则有(n-r)个产品未失效．记：

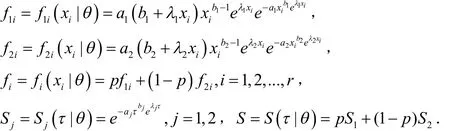
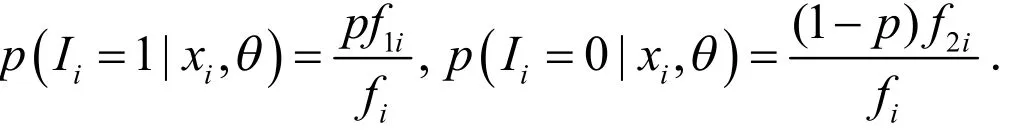
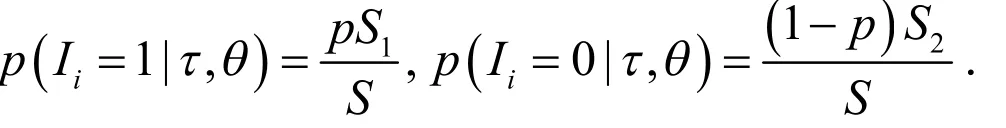
给定初始值(0)θ 的ECM算法的步骤为：

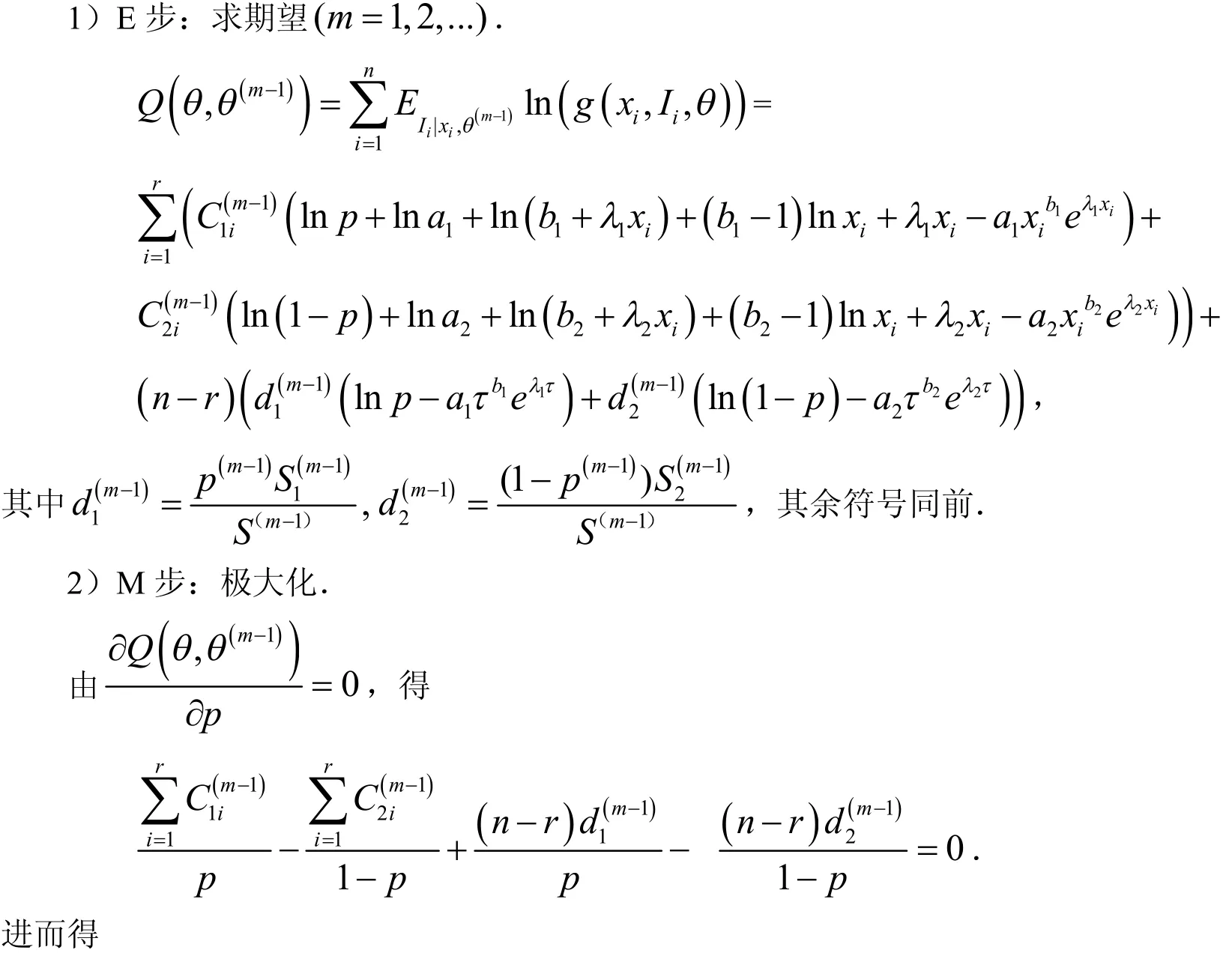
4 结论与讨论

混合改进威布尔分布是寿命数据分析中一个重要的统计模型，但是利用传统的统计方法如矩估计、极大似然估计等来估计模型参数是比较困难的．在混合 NMWD分布中，待估参数为，本文在利用ECM算法对混合NMWD分布进行参数估计时，只能得到p,a1,a2的显示解，而无显示解，文中用牛顿迭代法得到的近似解．本文为混合NMWD分布的参数估计提供了一种有效方法，不过还存在一些地方需要探讨，比如文中为了让算法介绍的清晰性和简洁性，只讨论了两个分布的混合，而两个总体的样本区分度在小样本场合或数据缺失较多的情况下，该方法参数估计的效率较低．牛顿迭代法具有二阶收敛速度，且方法简单，不过其初始值的选取比较苛刻，由此可尝试用其他迭代方法（如Chebyshev迭代算法[11]）对混合NMWD分布进行参数估计．

参考文献

[1] Lai C D,Xie M,Murthy D N P. A modified weibull distribution [J]. Ieee Transactions on Reliability,2003,52(1): 33-37.

[2] 严晓东，马翔，郑荣跃，等．三参数威布尔分布参数估计方法的比较[J]．宁波大学学报（理工版），2005，18（3）：301-305.

[3] 汤银才，侯道燕．三参数Weibull分布参数的Bayes估计[J]．系统科学与数学，2009，29（1）：109-115.

[4] 蒋卉，汤银才．混合Weibull分布参数估计的ECM算法[J]．系统科学与数学，2010，30（1）：79-88.

[5] 张锡清．混合三参数威布尔分布的参数估计[J]．哈尔滨电工学院学报，1996，19（1）：1-7.

[6] Dempster A P,Laird N,Rubin D B. Maximan likelihood estimation from incomplete data via the EM algorithm (with discussion) [J]. J Roy Statist Soc B,1977,39: 1-38.

[7] Meng X L,Rubin D B. Maximum likelihood estimation via the ECM algorithm [J]. A General Framework Biometrika,1993,80(2): 267-278.

[8] 茆诗松，王静龙，濮晓龙．高等数理统计[M]．2版．北京：高等教育出版社，2006：427-439.

[9] 康兆敏，方秀男．数值计算方法[M]．2版．北京：清华大学出版社，2013：32-42.

[10] 茆诗松，汤银才，王玲玲．可靠性统计[M]．北京：高等教育出版社，2008：97-108.

[11] 李光辉，张洪，叶绪国．混合Weibull分布参数估计的MCEM算法[J]．重庆师范大学学报（自然科学版），2015，32（2）：123-132.

Parameter Estimation of the Mixture Newly-Modified Weibull Distribution Based on ECM Algorithm

LIU Xiaoning
(College of Mathematics and Information Science,Wenzhou University,Wenzhou,China 325035)

The paper probes into the mixture newly modified Weibull distribution which is an important statistical model in life data analysis. However,it is quite different to estimate the parameters of the model by means of traditional statistical methods such as the moment estimation,the maximum likelihood estimation (MLE). The application of the ECM algorithm combined with Newton iterative method to study the complete sample data occasion with the mixture newly modified Weibull model under the normal operating conditions,the parameter estimation problem of censored data occasion. The maximum likelihood estimation (MLE) of all parameters under the relevant data occasion is thereby obtained.

The Mixture Newly-modified Weibull Distribution; ECM Algorithm; Newton Iterative Method; Complete Sample Data; Censored Sample Data

O213.2

：A

：1674-3563(2017)01-0001-11

10.3875/j.issn.1674-3563.2017.01.001 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：封毅)

2015-09-30

国家自然科学基金项目(11201345)；温州大学研究生创新基金(3162015028)

刘小宁(1991- )，女，河北邯郸人，硕士研究生，研究方向：应用统计与数理金融