一类非对称转子系统的全局动力学行为分析

刘熙娟，刘 云

(塔里木大学信息工程学院，新疆阿拉尔 843300)

一类非对称转子系统的全局动力学行为分析

刘熙娟，刘 云

(塔里木大学信息工程学院，新疆阿拉尔 843300)

研究了一类非对称性转子系统在1∶2内共振情形下的全局动力学行为．采用多尺度法和范式理论研究了系统的1∶2内共振，得到系统发生内共振的分岔方程，根据分岔方程得到了内共振非零解存在的条件．利用全局分析法研究了系统的Silnikov型同宿轨道及其存在性，获得了该转子系统的全局动力学行为．分析结果对抑制转子系统的内共振运动有一定的工程意义．

多尺度法；同宿轨道；非对称性转子；范式理论

转子系统在汽轮发电机中有着重要作用，这类机械系统一旦受到外部干扰，其速度就会发生很大变化，若要改变这种动力学行为，就要避免系统产生混沌现象．两个截面主惯矩不相等的转子称为非对称转子，非对称转子在工程中应用广泛．这类转子系统的最大特点是转轴在两个主方向上的刚度不同，因而这类转子系统的动力学特性与对称转子的动力学特性有很大差别．同时，为了适应旋转机械高速、高效的需求，转子与定子间的间隙越来越小，导致碰摩故障不断发生．在工程实际中，航空发动机、汽轮机等旋转机械存在许多原因造成转子系统具有非对称支撑的特点，容易导致整个机器较大振动，因而研究非对称转子的碰摩特性是非常重要和必要的．前人已做了大量工作[1-5]．肖锡武等[1]研究了具有非轴对称刚度转轴的分岔；王培杰等[2]利用有限元分析了非对称转子的动力学行为；Kwanka[3]研究了转子的动态系数；韩清凯、肖锡武等[4-5]分别研究了故障转子系统的非线性振动分析与诊断方法和不对称转子系统的参激强迫振动．本文主要研究了一类非对称转子系统在1∶2内共振情形下的全局动力学行为．

1 数学模型

在图1所示的外部支撑转子中，仅考虑圆柱形模型时，转子的位置就由两自由度ux,uy唯一来决定．

非对称刚度支撑的转子[6]可用下式表示：

图1 非对称刚性支撑的转子模型

其中m是转子质量，c是黏带阻尼系数，kij是刚度系数，ε是无量纲偏心距．转子被间隙δ限制在一个固定空间，δ为静止时转子与定子之间初始间隙．当转子的径向位移超过该间隙时，转子就会和定子接触．为便于数值模拟，令τ=nt，则系统（1）转化为：

2 多尺度法获得规范型

对于系统无量纲方程（2），为了方便多尺度法研究，不对称转子系统幂级数模型可表示为：

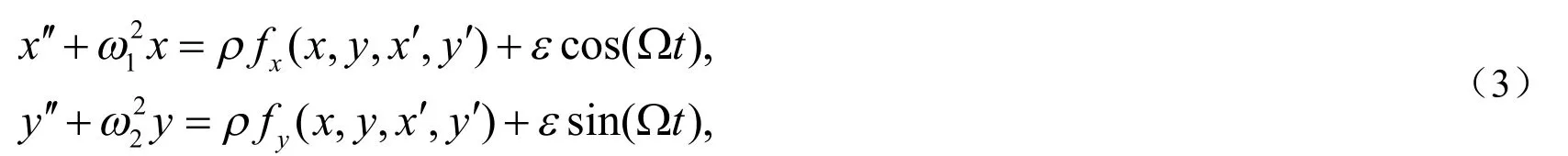
其中σ1,σ2为调谐参数．

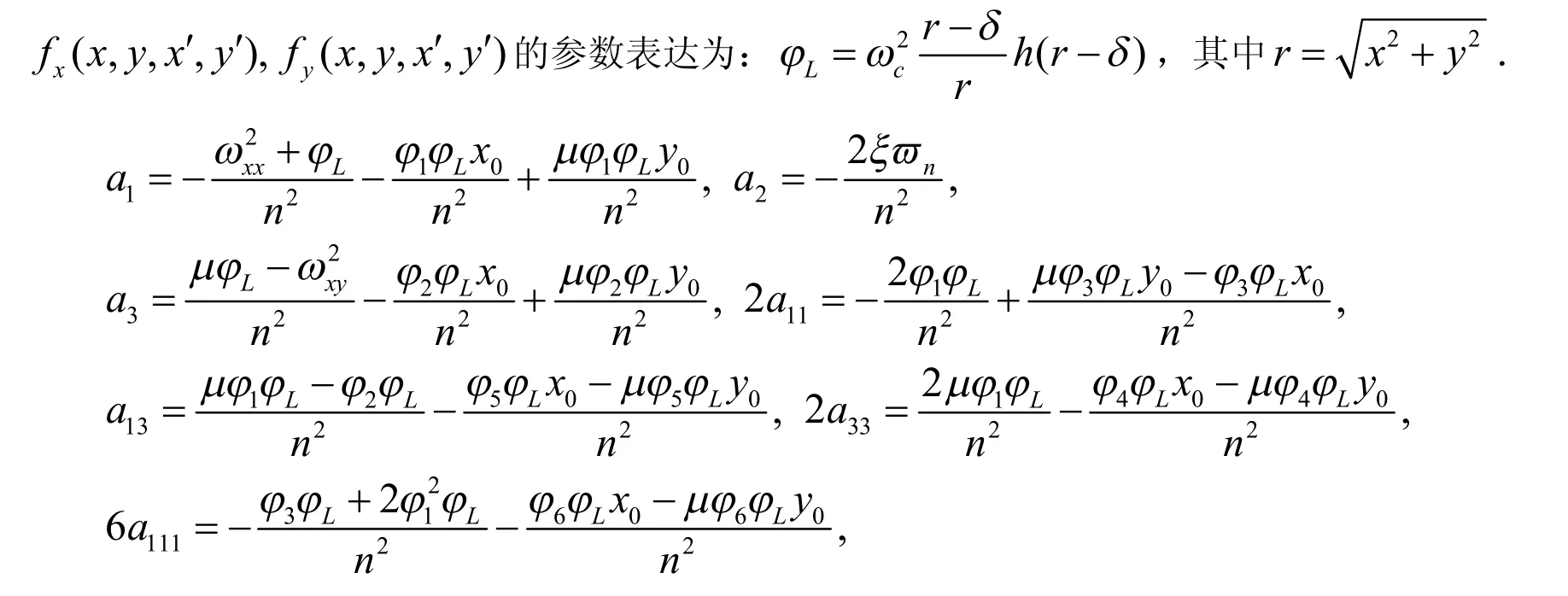
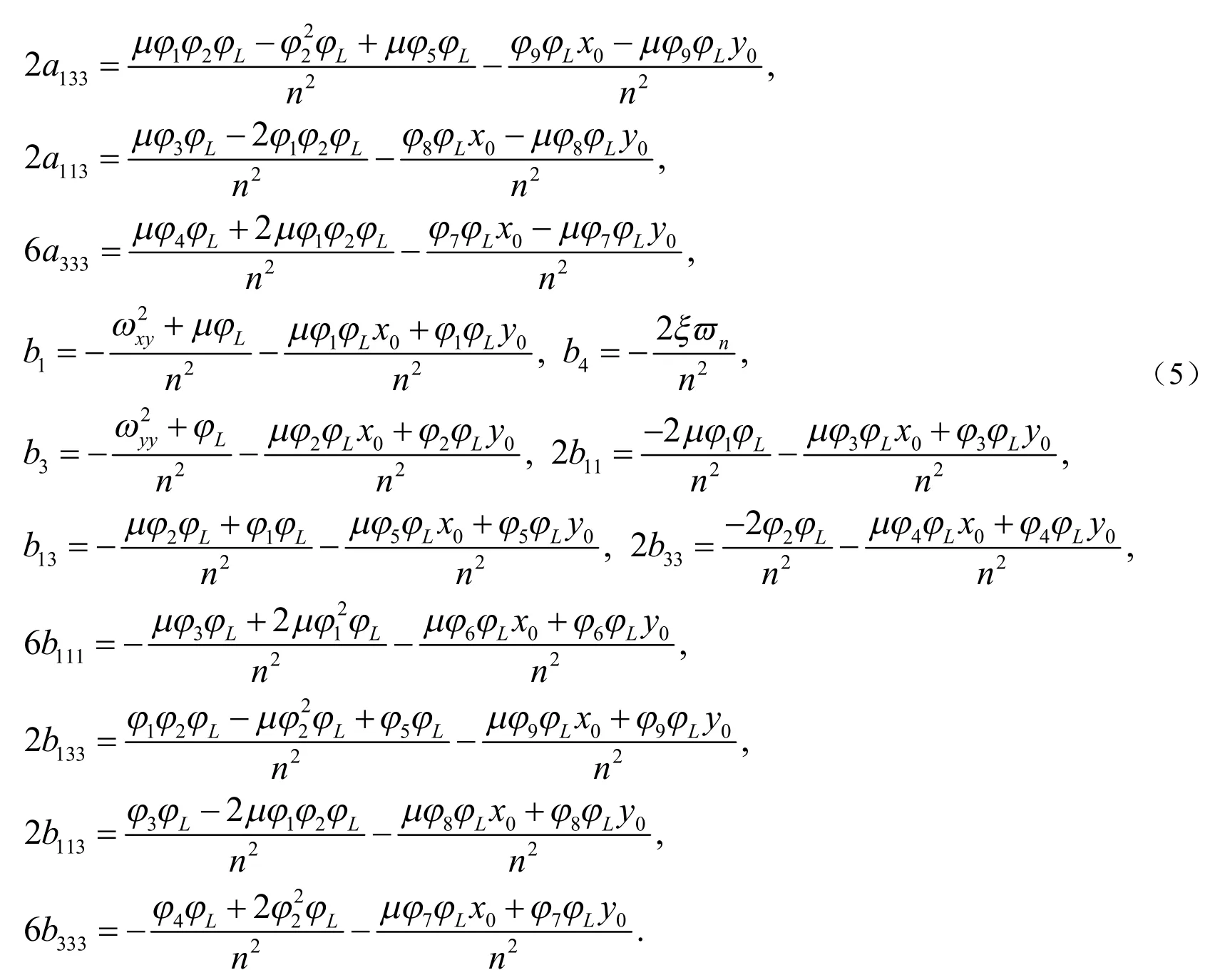
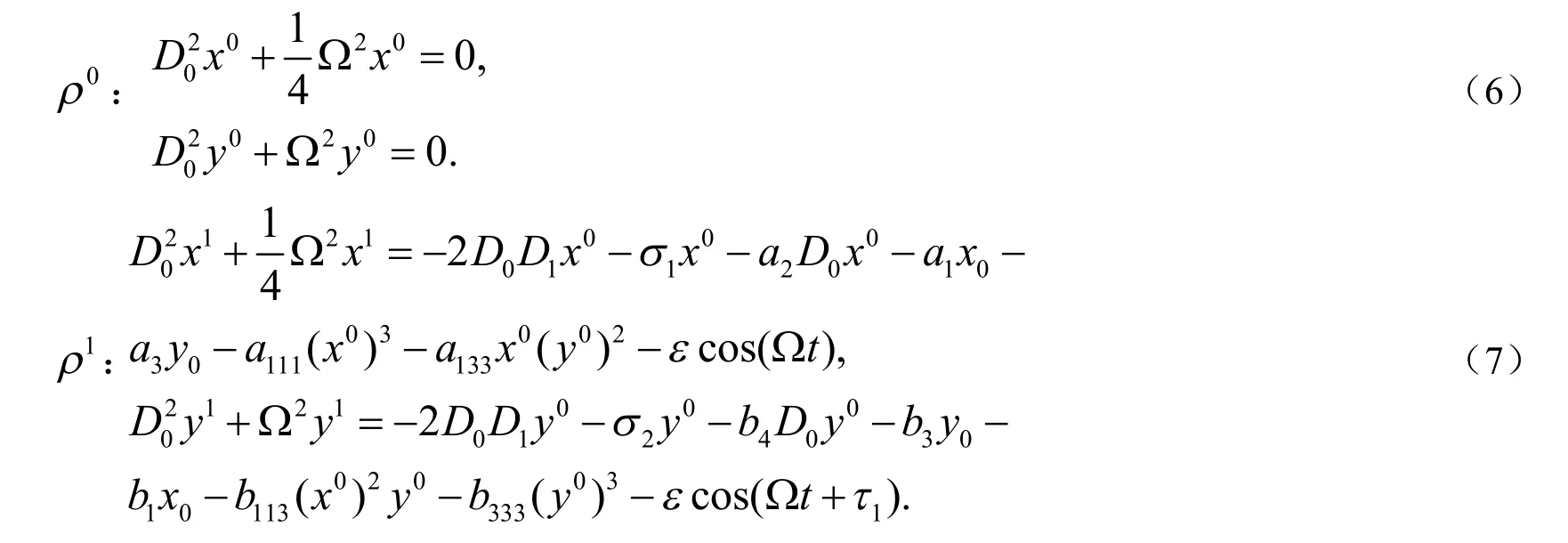
方程（6）的通解可表示为：

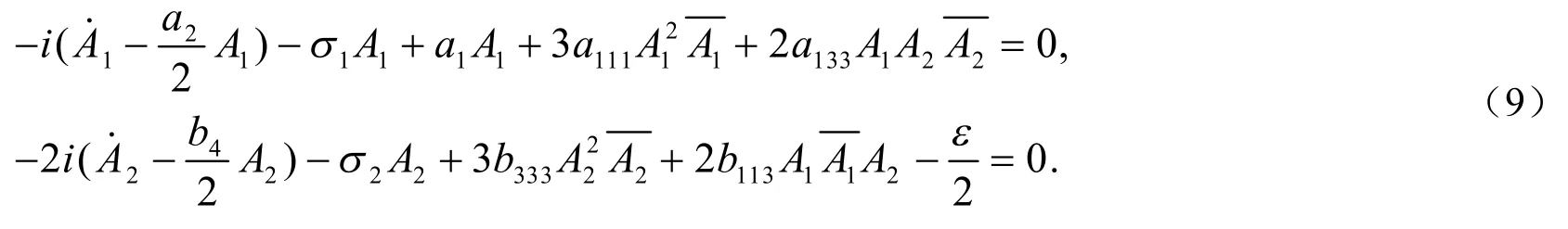
式（9）中的首项是对时间T1的微分，令：

把式（10）代入式（9），并将所得结果的实部和虚部分离，可得直角坐标形式的平均方程：

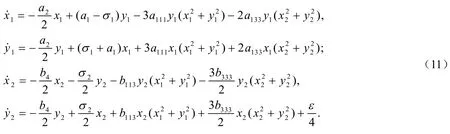
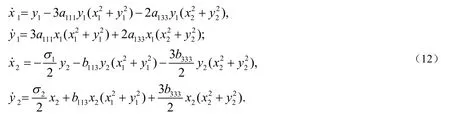
献[8]中范式理论和Maple程序可得到系统（12）的范式为：

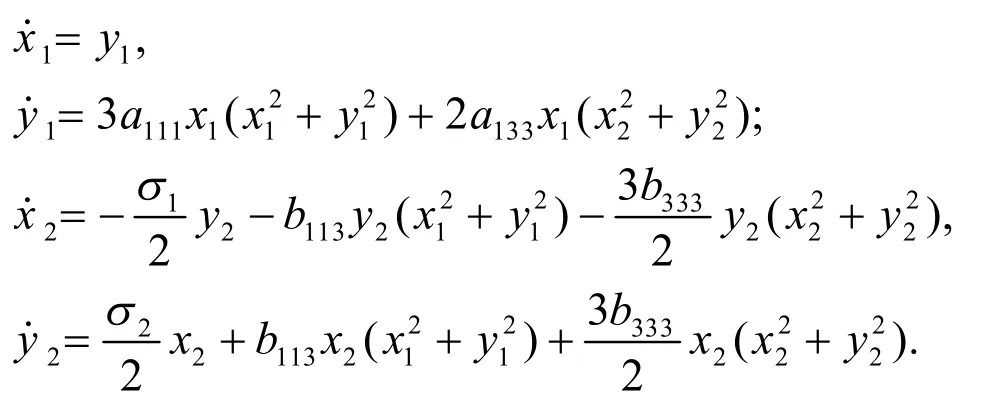
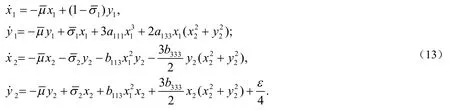
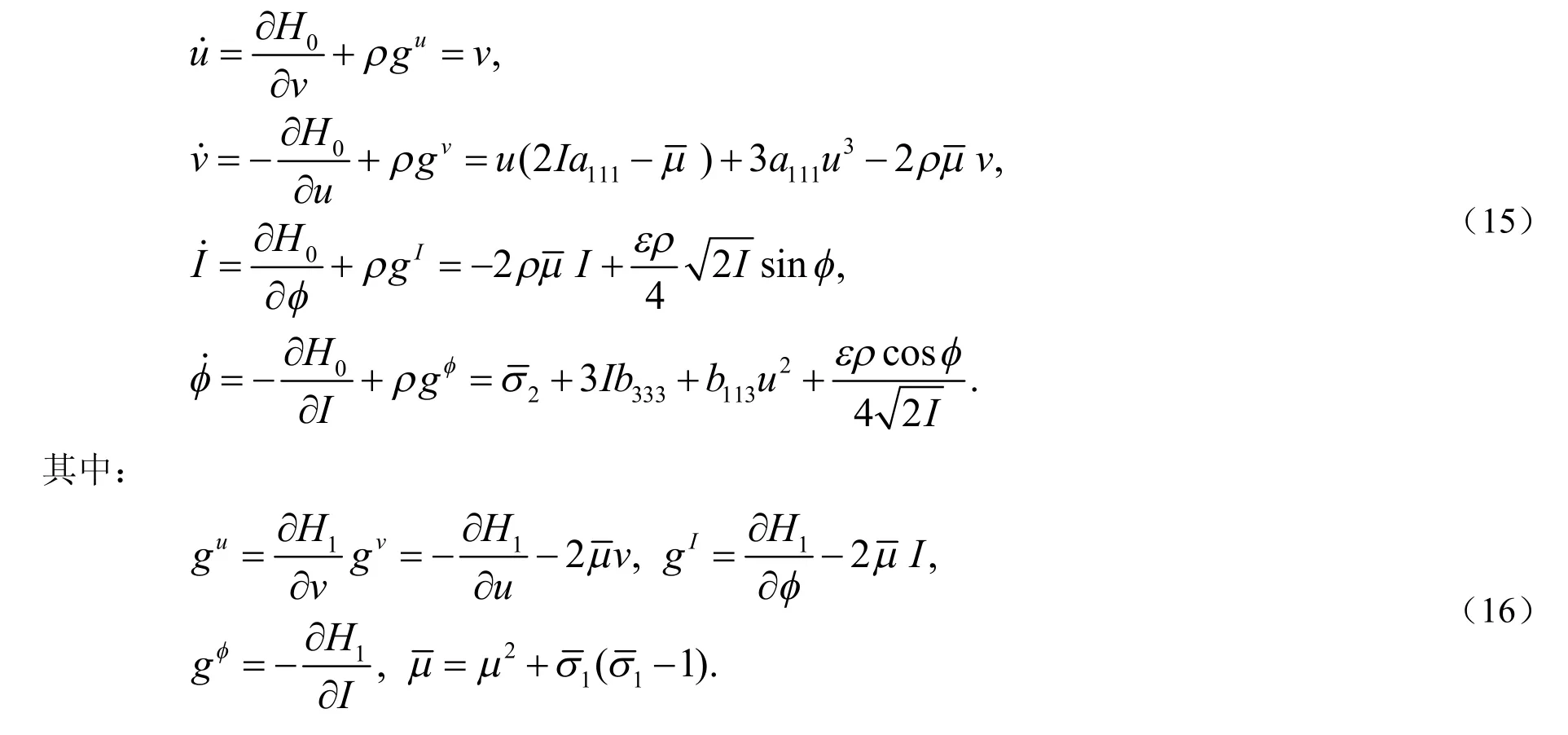
3 未扰动系统的全局分岔分析

令ρ=0，得到系统（15）的未扰动方程如下：

显然系统的前三个方程与φ无关，I是个常数．这样的话(u,v)平面的动力学行为与(I,)φ平面的行为是互相解耦的．(u,v)相空间中的所有的平衡点描述如下：

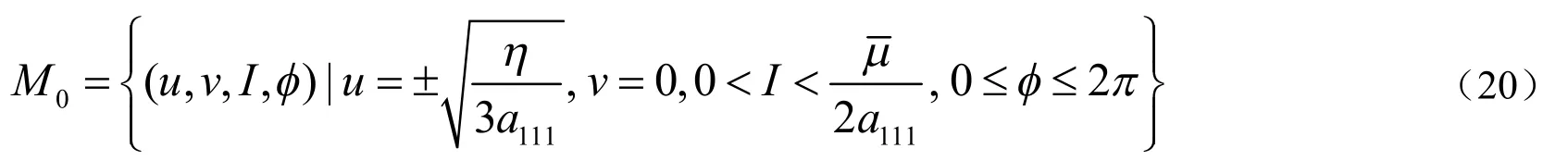
是一个两维不变流形．由参考文献[9]可知这个二维不变流形是正规双曲的．这个二维正规双曲不变流形有三维稳定和不稳定流形，分别用表示．系统（18）中，连接奇点的异宿轨道的存在表明沿三维异宿流形非横截相交，此流形Γ定义如下：

详实的解释汇报得到了甲方专家的一致肯定，李淑荣为履约践诺而表现出来的敬业精神更是得到了甲方的高度赞赏！

为了分析系统（18）的异宿分岔，得到未扰动系统的异宿轨线的分析表达式：

此外，常规双曲流形M0由下面的方程决定：

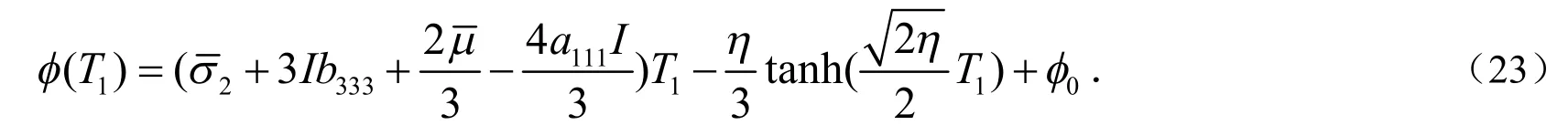
4 扰动系统的全局分岔分析

由公式（20）知M0是正规双曲不变流形，在充分可微的小扰动下，M与它的稳定流形和不稳定流形是不变的，因此有，可得：

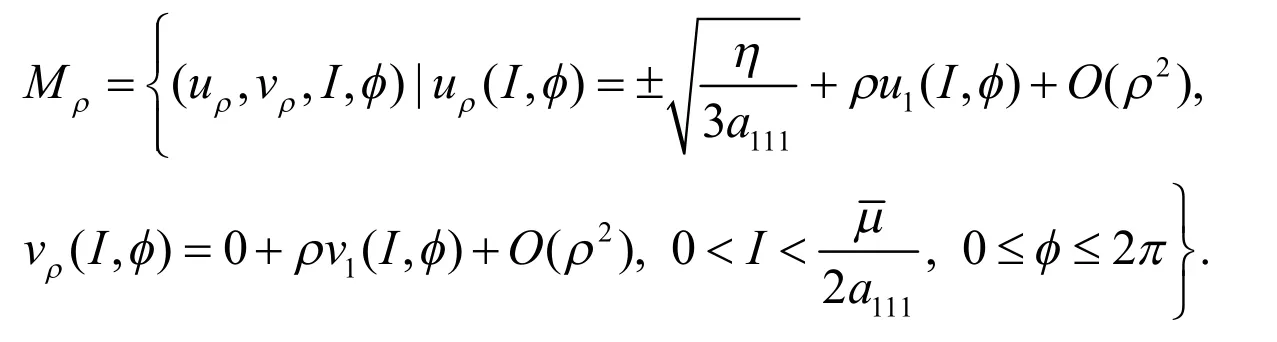
这样限制在Mρ上的（18）的扰动方程描述如下：

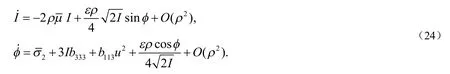
将以上变换代入（24），可得

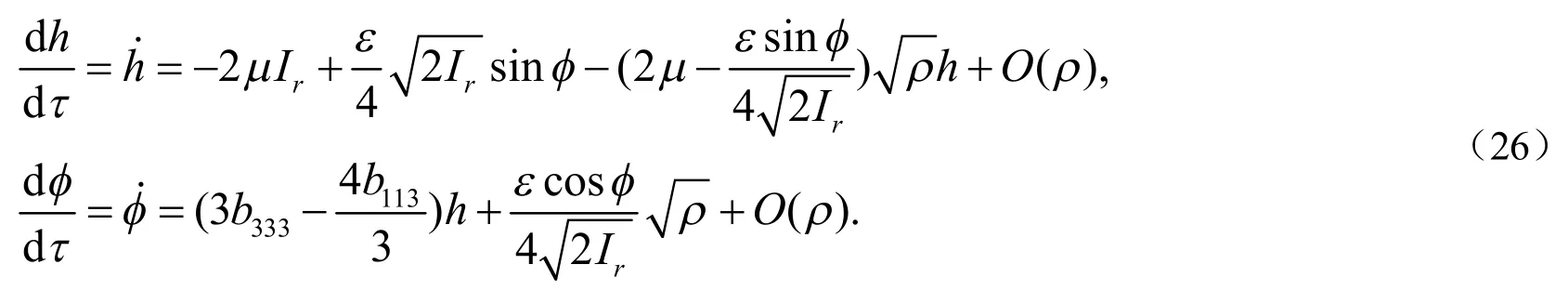
当ρ→0，系统（26）就变为：

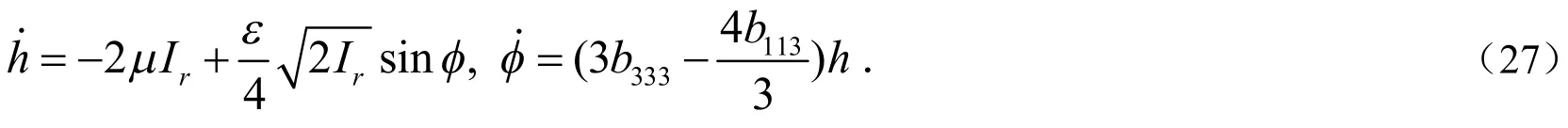
未扰系统（27）是带有Hamilton函数的Hamilton系统，其Hamilton函数为：

系统（27）的不动点为：

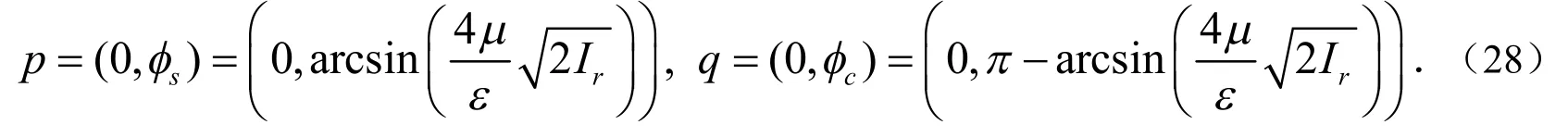
对不动点（28）对应的雅可比矩阵研究可知P是鞍点，q是中心．这样存在一个同宿轨道连接p和它本身．根据Kovacic[9]分析，对于充分小的参数ρ，q会成为汇qρ，p依然是鞍点pρ．此时中心q周围的周期轨道消失，连接p和p自身的同宿轨道也会消失，并有不稳定流形慢慢靠近qρ．

接下来，考虑Ir邻域上的Mρ动力学行为．此环形邻域定义如下：

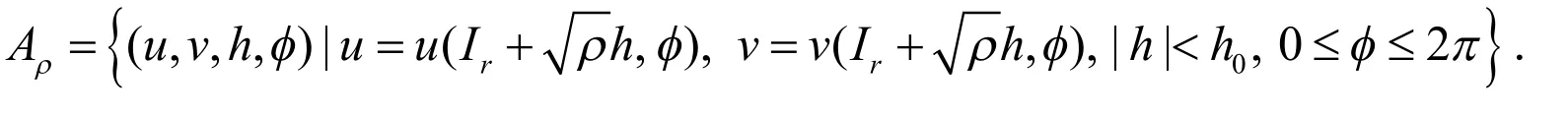
对于不动点的鞍-焦点类型的同宿轨道的存在会导致混沌的发生，这种同宿轨道类型称为Silnikov同宿环[10]．由文献[10]可知系统最后产生了Silnikov型同宿环，如图2所示．

图2 Silnikov型鞍焦点同宿轨道

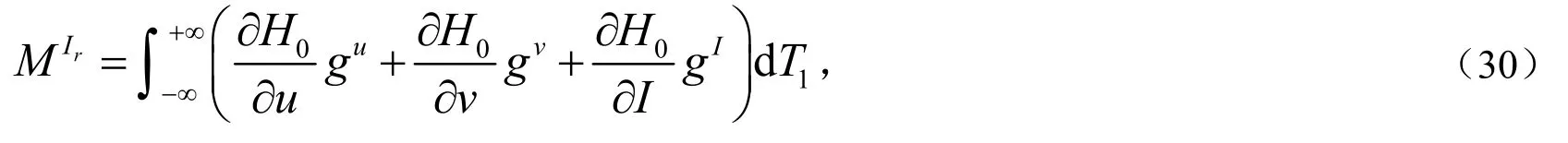
根据前面的分析以及参考文献[9]的结论，式（30）可以表示成下面的形式：

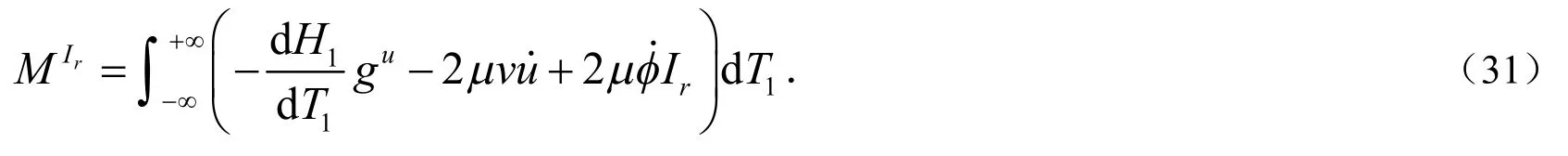
对式（31）的首项，第二、三项可以进一步简化，最后可得Silnikov函数（31）的表达式：

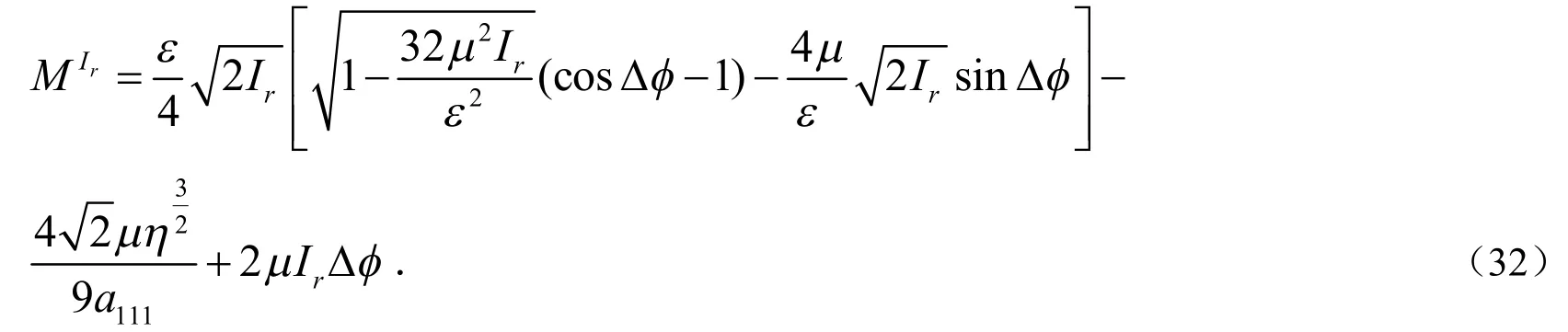
为了确定Silnikov型同宿轨道的存在性，首先要求Melnikov函数有一个简单零点．也就是说

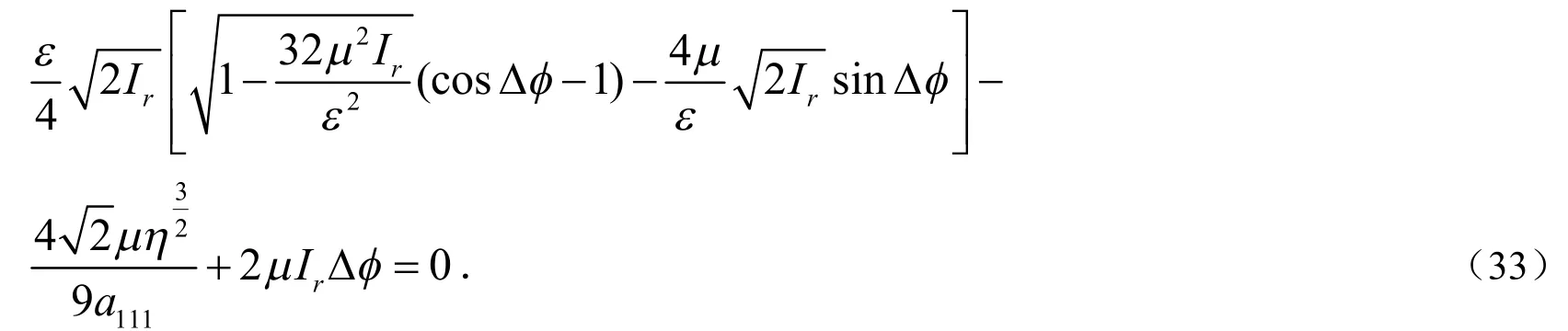
5 结 论

研究了一类非对称转子在 1∶2共振情形下的全局分岔和混沌等动力学行为，运用多尺度法和范式理论获得了标准型，借助高维系统 Melnikov理论以及其共振情况的延伸，分析了系统的全局分岔行为，最后探究了Silnikov同宿轨道的存在性，它是系统出现混沌现象的主要原因．

[1] 肖锡武，徐鉴，李誉，等．具有非轴对称刚度转轴的分叉[J]．力学学报，2000，32（3）：360-366.

[2] 王培杰，滕弘飞，刘笃金，等．非对称复杂转子系统有限元动力分析[J]．固体力学学报，1991，12（4）：370-375.

[3] Kwanka K. Dynamic coeffieients of stepped labyrinth gas seals [J]. Journal of Engineering for Gas Turbines and Power,2000,122(3): 473-477.

[4] 韩清凯，于涛，王德友，等．故障转子系统的非线性振动分析与诊断方法[M]．北京：科学出版社，2010：89-103.

[5] 肖锡武，肖光华，杨叔子．不对称转子系统的参激强迫振动[J]．振动工程学报，2002，15(3)：315-318.

[6] Varney P,Green I. Nonlinear phenomena,bifurcations,and routes to chaos in an asymmetrically supported rotor stator contact system [J]. Journal of Sound and Vibration,2015,336: 207-226.

[7] 刘习君，贾启芬．工程振动理论与测试技术[M]．北京：高等教育出版社，2004：292-307.

[8] Zhang W. Global and chaotic dynamics for a parametrically excited thin plate [J]. Journal of Sound and Vibration,2001,239(5): 1013-1036.

[9] Kovacic G,Wiggins S. Orbits homoclinic to reasonance with an application to chaos in a model of the forced and damped sine-Gordon equation [J]. Physica A,1992,57: 182-225.

[10] Feng Z C. On the existence of chaos in a parametrically forced mechanical systems with broken O(2) symemetry [J]. Zeitschriftfuer Angewandte Mathematic and Physica,1993,44: 201-248.

Behavioral Analysis on Global Dynamics of an Asymmetric Rotor System

LIU Xijuan,LIU Yun
(College of Information Engineering,Tarim University,Aral,China 843300)

The global dynamic behavior based on 1: 2 internal resonances is studied by adopting the methods of multiple scales and the normal form theories,from which the bifurcation equation of the system is obtained. According to the bifurcation equation,the existence condition of untrivial solutions of the internal resonance is secured. The extension of Silnikov homoclinic orbit is studied via the global perturbation method,thus the global dynamical behavior of the rotor system is received. The result of such analysis has some engineering significance towards the internal resonance motion to restrain the rotor system.

Multiscale Method; Homoclinic Orbit; Asymmetric Rotor; Paradigm (Normal Form) Theory

O193

：A

：1674-3563(2017)01-0020-10

10.3875/j.issn.1674-3563.2017.01.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：封毅)

2015-07-13

甘肃省国际科技合作计划项目(1104WCGA195)；甘肃省自然科学基金资助项目(1208RJZA111)；甘肃省教育厅硕导基金项目(212104)

刘熙娟(1988- )，女，甘肃会宁人，讲师，硕士，研究方向：非线性动力学