多楔带传动系统带横向振动的计算及图像分析
2017-03-01汪恩军廖义德雷进宇
汪恩军,何 超,廖义德,肖 俊,雷进宇
(1.武汉工程大学 交通研究中心,武汉 430074;2.武汉工程大学 机电工程学院,武汉 430205;3.武汉理工大学 智能交通系统研究中心,武汉 430063)
多楔带传动系统带横向振动的计算及图像分析
汪恩军1,何 超2,廖义德2,肖 俊2,雷进宇3
(1.武汉工程大学 交通研究中心,武汉 430074;2.武汉工程大学 机电工程学院,武汉 430205;3.武汉理工大学 智能交通系统研究中心,武汉 430063)
为了全面地分析多楔带的横向振动问题,以多楔带传动系统为研究对象,将带段简化成轴向运动粘弹性弦。首先建立带横向振动计算的数学模型,应用Galerkin法将带的时间-空间连续方程离散成为时间和空间函数之积,计算多楔带的横向振动。然后用图像处理的方法对多楔带横向振动参数和轮-带滑移率进行实测分析。将振动模型轴向运动弦线的计算值与图像分析值进行对比,结果表明,当带速较低时,计算值和实验值吻合较好,该计算方法和实验方法对多楔带前端附件系统带横向振动的研究分析具有参考价值。
振动与波;多楔带传动;横向振动;图像分析
多楔带传动系统是发动机轮系的主要组成部分,该系统主要由驱动轮、多个从动轮、张紧器和多楔带等附件组成,它具有传动平稳,柔韧性高,传递功率大等优点,已广泛地应用于汽车发动机工业中。多楔带传动系统的复杂性表现在工作时产生的各种振动,其振动形式主要包括两种:两相邻轮之间轴向运动带的振动、轮和张紧臂的旋转振动。轴向运动带的振动主要有纵向振动、横向振动、侧向振动以及扭转振动。对于轴向运动带振动的分析,已有研究表明横向振动是其主要形式,远大于纵向振动[1]。多楔带的振动不仅加快了带本身的磨损并产生噪声,甚至会导致传动系统损坏从而影响发动机的技术指标。因此多楔带横向振动的研究一直受到国内外学者的广泛关注。Ulsoy等学者最早开始研究带的耦合振动,研究成果表明了带张力的变化会引起较大的横向振动,导致振动的不稳定[2]。Beikmann等人在横向振动问题上将系统简化成弦线耦合振动模型,将测试值和计算值进行了对比分析,为以后的研究奠定了理论基础[3]。上官文斌等以两相邻轮之间带为对象,将带简化成纵向黏弹性弦,分析了黏弹性参数对横向振动的影响[4]。Kong和Parker则采用Galerkin法计算了多楔带的振动,分析了多楔带弯曲刚度对带振动频率的影响[5]。以上成果在一定程度上促进了多楔带振动研究的发展,但多楔带振动特性的研究工作仍有待进一步探索分析。
1 多楔带驱动系统轮-带耦合振动建模与分析
1.1 轮-带耦合模型及方程的建立
图1为稳定状态下发动机多楔带传动系统示意图,包括驱动轮1、张紧器3、4、从动轮2、5、6以及多楔带等,ri和θi(i=1,2,3,4,5,6)表示驱动轮、张紧臂以及从动轮的半径和角位移;u1和u2分别表示带1和带2的纵向位移,W1和W2表示带段1,2的横向位移,βj(j=1,2)是张紧臂与相邻带段之间的安装夹角。L1和L2表示带段1,2的长度;kr为张紧器的等效刚度,Ce为张紧器等效黏性阻尼系数。
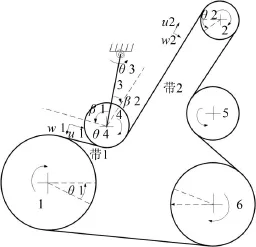
图1 多楔带传动系统示意图
在多楔带轮-带耦合模型中,带1和带2与张紧器耦合运动,本文只研究了三轮一带耦合振动部分。将各带段简化成轴向运动弦线,带的速度为一稳定值,忽略其弯曲刚度,假设带的物理特性一致,并以静态方式伸缩。应用Hamilton原理建立系统振动方程式然后线性化处理,得到各带段的横向振动微分方程式为[6]
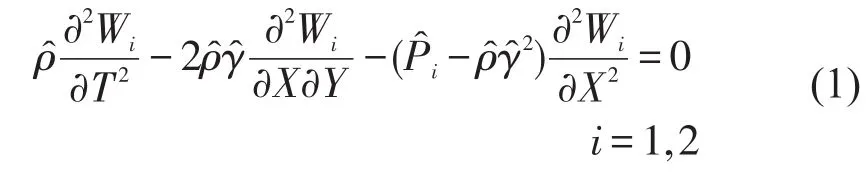
其中边界条件为

皮带轮的旋转角位移θj是根据参考状态下的新参数φj(j=3,4,5,6)来定义,其中φ1=0,θ与φ关系为

在无量纲情况下,系统振动微分方程为

1.2 轮-带耦合振动求解
多楔带的振动方程表示的是连续体的运动,是多自由度的线性方程。而从动轮与张紧器旋转振动的动态方程则表示的是离散体的运动,为单自由度运动。系统数学模型由微分方程或偏微分方程、代数方程等组成,为了应用离散系统振动方程的求解方法,计算时应用Galerkin法离散成为时间函数和空间函数之积,再将结果与张紧臂的离散方程相结合,方便系统振动方程的计算[6]。选取带的横向振动方程进行离散,设
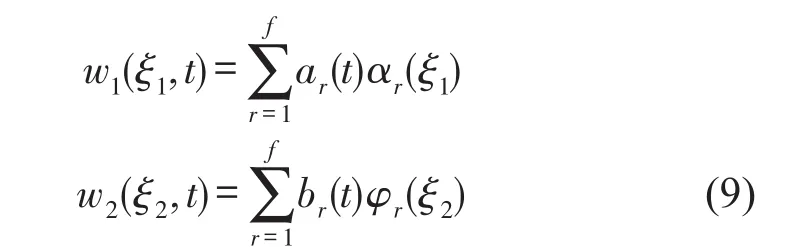

广义坐标ar(t)、br(t)和θt(t)的约束满足式(3)的边界条件

引入未知的Lagrange因子η保证式(11)、式(12)边界条件,应用拉格朗日方法将系统振动方程改写为矩阵方程
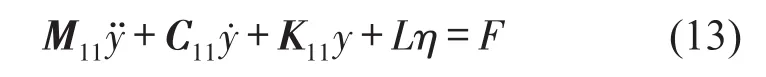
式(13)中的η通过左乘矩阵CT来消除,矩阵C的计算条件是CTL=0,该条件是通过分解矩阵L的奇异值而得到,矩阵L=U(n+2f)×(n+2f)σ(n+2f)×2V2×2,是2阶矩阵,而U、V是正交矩阵,所以σ的主对角线中有两个非零的奇异值。保留矩阵U中零奇异值的列,消除非零奇异值的列从而得到矩阵C,令(13)中的y=C∙z,将方程式(16)左右同时左乘矩阵CT,消除Lagrange因子η,得到离散方程żz̈
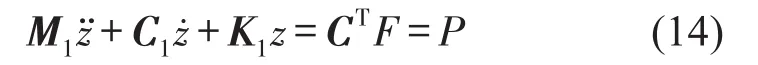
式 (14)中 有M1=CTM11C,C1=CTC11C,K1=CTK11C,其中M1是质量运算符,C1是回转算子,K1是刚度运算符。应用复模态理论方法求系统的固有频率,先将式(14)转换成以下形式

令状态向量和激励向量为

矩阵微分算子为
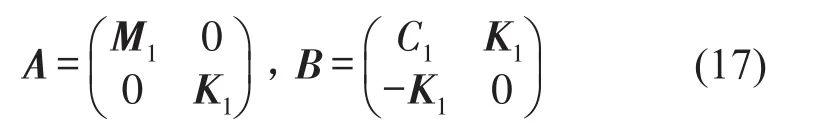
复模态矢量Ea、Vb为系统方程的左右特征矢量[7],得到方程
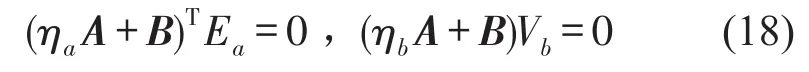
其中E=(E1,E2,...,E2N)和V=(V1,V2,...,V2N)是系统方程的左右模态矩阵,N为振动微分方程(14)的维数。由式(18)可以确定ηa=ηb是系统的特征值,而η共轭成对出现,η的虚部表示系统振动的固有频率。为了求解系统的稳态振动响应,将模态矩阵表示成为
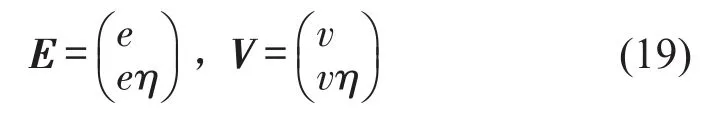
式(19)中e、v分别为式(15)的左右模态矩阵,通过复模态变换U=Dh代入式(15),并且方程左右两端同时左乘以ET得到

矩阵ETAD和ETBD均为对角矩阵,所以有ETAD=diag(Ad)和ETBD=diag(Bd),方程式(20)可以写成

经过上述计算分析,系统振动方程完全解耦,可用于多自由度线性振动方程的求解,得到任意激励下系统的振动响应。
驱动轮的角位移是系统激励的来源,力矩来自于交流电机,通过曲轴带动驱动轮。激励较为平稳,实验中令驱动轮1的角位移为500 r/min,角位移波动表达式为
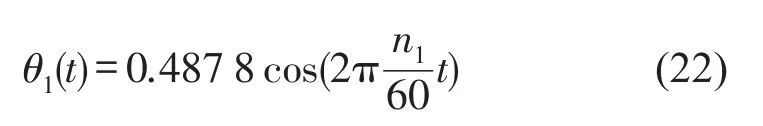
θ1(t)表示驱动轮1的角位移,t表示时间变量,单位以秒计,n1是驱动轮的转速,单位按照计算。
2 带横向振动的图像实测分析
2.1 测试对象与设备
轮-带耦合振动特性测试是在发动机试验平台上完成,测试系统由五轮-带传动系统,高速摄像机,角度编码器,激光位移传感器,驱动电机等组成。测试对象有多楔带的横向振动参数、轮带间滑移率等。图2为搭建的实验平台图。

图2 实验平台
驱动轮由交流电机带动,通过变频器控制速度大小。角度编码器连接驱动轮和从动轮测量速度。选取240帧/秒的高速摄像机置于试验台前端对驱动轮与从动轮之间的带段运动特性进行采样,测量多楔带的轴向运动规律和带段的横向波动特性,测试是在低速空载条件下进行。
2.2 从动轮-带滑移率测试方法
多楔带传动系统的动力是来自驱动轮的转矩,带与带轮间通过摩擦力带动附件运转。从动轮的半径大小为R2,与从动轮同步转动的角度编码器通过传动比例换算成角速度w1,稳定转速下,通过近景摄影提取带段上一固定标志点中心坐标的运动长度L,通过提取的振动图像的帧速率和帧数目获取在该过程中所经历的时间t,换算出带的线速度,对以上的数据参数单位进行标准统一化,以驱动轮的转速作为参考条件,从动轮的滑移率公式为

2.3 滑移率测试结果分析
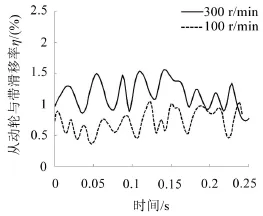
图3 从动轮-带滑移率
2.4 带段横向振动参数图像测试方法
多楔带传动系统两轮间的带段运转过程中引起的振动主要是横向振动,假设多楔带各带段的物理特性一致,忽略各轮绕固定转轴所做的旋转振动。将多楔带简化为纵向运动弦线,对张紧轮和从动轮之间的带段进行测试。利用近景摄影测量,在该带段上任意选取一个合适的标志点,标志点跟随多楔带运动,摄像机对标志点进行跟踪识别。提取摄影图像的多帧图片,按顺序跟踪系列图片中的同一个标志点,提取该标志点中心坐标,经过一系列图像处理[8],绘制出标志点运动轨迹,图像处理过程流程图见图4。
2.5 带段横向振动测试结果与分析
多帧图像中提取到的标志点的运动轨迹即为多楔带的波动图像。在空载条件控制下当驱动轮转速为时,多楔带标志点经过图像处理得到带段从张紧轮到从动轮之间的横向波动轨迹见图5。
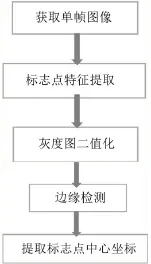
图4 多楔带标志点图像处理流程

图5 横向振动波形图
由图5可见,当标志点运动到带段中间时振动位移相对较大,靠近两轮时的振幅较小。在稳定的运行工况下,柔性带的波动是不规则的,波动幅值也不均匀,本文中,高速摄像机采集轴线上的空间一固定点在动态情况下运动图像,通过波形分析找到运动过程中偏离静态弦线的最大位移即为波动幅值。通过分析得知出在相对稳定的工况下带段的振动幅值在带段中间位置处于最大。柔性带周期性波动的频率借助波动形状获取:跟踪标示点轨迹,当其运动轨迹出现重叠并呈周期性变化时,由一个周期内所采集的图片数目得到波动频率,该实验中,稳定状态下的带横向振动频率约为15Hz~17Hz。以此推广到不同带速条件下的横向振动特性分析。
3 计算模型验证及分析
为了检验多楔带横向振动计算方法的准确性,采用图像处理的方法对带的横向振幅,波动周期及频率等进行了实测,将较低速条件下得到的实测结果与轮带耦合振动计算模型结果进行对比,验证计算模型的可行性,对多楔带附件驱动系统带横向振动参数的计算进行完善。传动系统的各带段的张力均为650 N,带的弹性模量EA=170 kPa,张紧臂弹簧的等效扭转刚度kr=16.7 N∙m/rad,β1,β2分别为75°、45°。
3.1 从动轮与带之间的滑移率
空载条件下,当系统稳定运转时,从动轮与多楔带之间的的滑移率为
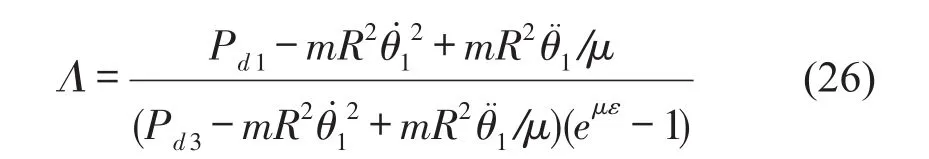
式(26)中Pd1、Pd3分别为带1和带3的张力,θ1为轮1的转角,带与轮间摩擦系数为μ,m为线密度,ε为带与轮之间的包角,R为轮中心到带横截面中心的距离。稳定状态下,当负载扭矩为0时,系统在一个相对较低的速度运转,将轮1的角位移以及系统已知参数m=0.091 kg,R=0.055 m,μ=1.2带入式(26)中,再将上述已知条件代入图像分析的测试方法中,得到从动轮-带之间滑移率的实测值与计算值见图6。

图6 从动轮与带间滑移率
由图6可知,滑移率的计算值和实测值并不是完全一致,这是因为实际运动中带具有黏弹性,张力的波动会给实际滑移率的测试造成影响。但是滑移率的波动响应幅值计算和测试基本吻合,因此文中的计算分析方法和测试方法对系统多楔带的振动研究具有参考价值。
3.2 带2横向振动位移
工程上主要测量张紧器与从动轮之间最长带段的横向振动位移,本测试中测量了和张紧器相连的带段2横向振动的位移。带段是一种结构布局上的约束而不是参数激励,计算该带段的横向振动位移可采用本文的建模方法。在空载条件下,当驱动轮转速为时运用横向振动模型计算方法和测试方法进行分析,带2中点处的横向振动位移计算值与经过两轮之间带段的图像分析实测值见图7。
两轮间带段中点处的振动响应计算值呈现一定规律性。而带段在两轮间的整个振动响应过程实测值呈现不规则性。由图7时间段的中点处可知,实测值和计算值的横向振动位移相差不大,由于带段匀速运动,多楔带运动到在中点处的测试值和带段中点处的计算值基本吻合。稳定转速下带段2横向振幅实测值靠近张紧轮和从动轮处最小,在带段中点处最大。由于带段的黏弹性和实验台共振的影响,波动形状略有差异,但带段中点幅值基本吻合,从而验证了本文的模型计算方法和图像测试横向振动位移方法的可行性。带段的振动是随着机械的运转而存在,无法完全消除,只能在合理的范围内控制和减小。减小多楔带横向振动位移,不仅能提高多楔带传动系统的效率、减小噪声,还能增加带的使用时间,因此对多楔带的横向振动的研究具有重要的意义。

图7 带2横向振动位移计算值与实测值
4 结语
轮-带耦合振动系统模型的数学计算方法应用广泛,实用性强。图像分析得到的带段在中点的横向振动位移实测值与计算值基本吻合,振幅相接近,证明了本文的横向振动模型计算方法和图像分析的正确性;两轮间带段的横向振幅靠近张紧轮和从动轮处最小,在带段中点处最大;从动轮-带滑移率在较低速度条件下随着驱动轮转速的增加而增大;图像分析方法能够在较低速条件下重构多楔带的横向振动波形图,因此能更直观地反映出多楔带各横向振动参数。
本文在探索该传动系统运动特性检测方法的基础上,更加全面、深入地研究发动机轮系的动态特性,有利于提高汽车发动机轮系的设计能力,具有重要的理论意义和现实意义。研究分析轮系的振动特性,降低轮系的振动、噪声及油耗,提高驾乘舒适性,进而推动轮系产品设计技术水平的进步。
[1]戈新生,李德双.轴向运动带的横向与纵向非线性振动[J].机械强度,2012,34(1):020-024.
[2]ULSOY A G,WHITESELL J E,HOOVEN M D.Design of belt-tensioner systems for dynamic stability[J].ASME Journal of Vibration,Acoustics,Stress,and Reliabilityin Design,1985,107:282-290.
[3]BEIKMANN R S,PERKINS N C,ULSOY A G.Free vibration of serpentine belt drive systems[J].ASME Journal of Vibration andAcoustics,1996,118:406-413.
[4]上官文斌,林浩挺.发动机前端附件驱动系统中带横向振动的计算与实测分析[J].内燃机工程,2013,34(2):24-29.
[5]KONG L,PARKER R G.Coupled belt-pulley vibrati-on in serpentine drives with belt bending stiffness[J].ASME Journal ofApplied Mechanics,2004,71(1):109-119.
[6]PARKER R G.Efficient eigensolution dynamic response and eigensensitivity of serpentine belt drives[J].Journal of Sound and Vibration,2004,270:15-38.
[7]上官文斌,张智,许秋海.多楔带传动系统轮-带振动的实测与计算方法研究[J].机械工程学报,2011,47(21):28-36.
[8]秦襄培,郑贤中.Matlab图像处理宝典[M].北京:电子工业出版社,2011.
Calculation and ImageAnalysis of Belt Transverse Vibration in Serpentine Belt Drive Systems
WANG En-jun1,HEChao2,LIAO Yi-de2,XIAOJun2,LEI Jin-yu3
(1.Transportation Research Center,Wuhan University of Engineering,Wuhan 430074,China; 2.School of Mechanical and Electrical Engineering,Wuhan University of Engineering, Wuhan 430205,China; 3.Intelligent Transport System Research Center,Wuhan University of Technology,Wuhan 430063,China)
The lateral vibration of a serpentine belt drive system is studied.First of all,the serpentine belt is simplified as an axially moving viscoelastic string.And the mathematical model for calculating the lateral vibration of the serpentine belt is established.Then,Garlerkin method is applied for discretizing the continuous equation of the belt to calculate the lateral vibration of the serpentine belt.Finally,the image processing method is used to measure and analyze the transverse vibration parameters and the slip rate between the pulley and the belt.The results show that the measurement and calculation data agrees well for low belt speed.The measurement and the optimization methods are useful for calculating and analyzing belt transverse vibration in serpentine belt accessory drive systems.
vibration and wave;serpentine belt drive;lateral vibration;image analysis
TH132.2;TK41
:A
:10.3969/j.issn.1006-1335.2017.01.002
1006-1355(2017)01-0005-05+15
2016-09-20
湖北省自然科学基金资助项目(2014CFB777);国家自然科学基金资助项目(51479155)
何超(1990-),湖北省黄冈市人,男,硕士研究生。
雷进宇,男,博士研究生,硕士学位.研究方向为数据可视化与可视分析。E-mail:jylei@whut.edu.cn
