有界窄带激励下的电磁开关系统主共振分析

杨志安，赵利沙

（1.唐山学院 唐山市结构与振动工程重点实验室，河北 唐山 063000；2.华北理工大学 机械工程学院，河北 唐山 063000）

有界窄带激励下的电磁开关系统主共振分析

杨志安1，赵利沙2

（1.唐山学院 唐山市结构与振动工程重点实验室，河北 唐山 063000；2.华北理工大学 机械工程学院，河北 唐山 063000）

以电磁开关系统为研究对象，研究电路与磁路耦合系统在有界窄带激励下的强非线性振动问题。建立电磁开关强非线性系统在有界窄带激励下的随机微分方程。应用改进的多尺度法得到系统的幅频响应方程，对窄带激励下系统主共振的稳定性进行计算，并分析系统各参数对系统主共振均方值的影响。结果表明，增大阻尼系数可以减小系统主共振的均方值；增大激励电压可以增大系统主共振的均方值；增大电阻可以减小系统主共振的均方值；增大随机扰动强度，极限环变化不大。

振动与波；电磁开关；改进多尺度法；窄带激励；均方值；强非线性振动

近年来，随着汽车市场的迅速发展，汽车已经成为日常生活中不可分割的重要组成部分。汽车起动机是汽车发动机的关键零部件，现代汽车中几乎每辆汽车都在使用，而电磁开关又是汽车起动机中的一种重要的控制元件，其工作原理是线圈通电后产生电磁吸力，使活动铁芯移动，接通励磁绕组电路，产生励磁，电枢工作，从而带动发动机起动。断电后，活动铁芯在弹簧力下复位，等待下次启动[1]。电磁开关的设计质量直接影响起动机的可靠性，因此对电磁开关的研究具有十分重要的意义。

文献[2]阐述了起动机用电磁开关的工作原理，依据原理探讨引起电磁开关触片、触点烧蚀的主要原因，并给出改善措施。文献[3]阐述了电磁开关的组成及传统结构形式的利弊分析，并进行改进。文献[4]研究非线性电阻电感型RLC串联电路的非线性振动，应用多尺度法，得到系统满足主共振条件的一次近似解以及对应的定常解。文献[5]研究环形极板机电耦合系统的强非线性问题。应用多尺度法求得系统的主共振的幅频响应曲线，分析了不同系统参数对共振的影响。文献[6]研究了Vander Pol-Duffing振子在窄带随机噪声激励下的响应问题。用参数变换法使方程出现小参数，用多尺度法分离了系统的快变项，讨论了系统的阻尼项、非线性项和随机项等参数对系统的影响。文献[7]从共振特征入手，对转子的弯扭耦合振动开展研究。

本文应用改进多尺度法研究电磁开关强非线性系统主共振在窄带随机激励下的响应[8]，得到主共振的幅频响应曲线和系统随机均方响应的近似表达式，考虑了随机项对电磁开关系统响应的影响。应用4阶龙格-库塔法计算出系统的时间响应曲线和相图，对电磁开关系统的设计与优化具有重要的参考意义。

1 有界窄带激励电磁开关系统强非线性动力学方程

窄带随机过程是指频谱密度集中在中心频率附近相对较窄的频率分布过程，它是工程中经常遇到的随机过程[9–10]，特点是频谱主要集中在某段区间上。

电磁开关的数学模型如图1所示，电源的电动势为U(t)，电阻为r，电路电流为i，线圈的自感为L(x)，电源、电阻及电感组成回路。电磁铁的质量为m，弹簧刚度为k，电磁铁线圈的自感为Lm(x)，x为自弹簧平衡位置算起的水平位移，电磁铁上线圈激励电压为Um，电磁铁上线圈电阻为R，电磁铁上线圈电流为im，M(x)为电路与电磁铁的互感，rv为线圈与磁铁之间的摩擦阻力系数。

图1 电磁开关模型

选位移x，电路电流为i，电磁铁上线圈电流为im为广义坐标。

将拉格朗日方程和损耗函数代入拉格朗日麦克斯韦方程[11]，建立系统的非线性动力学方程为

在式（2）中，随机电压U(t)控制电磁开关在静平衡位置附近的振动位移，进而分析电磁开关在有界窄带激励下的力学响应。U(t)为有界随机噪声，它是由电路中信号发动器发出信号，可表示为

式中H＞0为随机激励幅值，Ω为随机激励的中心频率，W(t)为标准的Winner过程，γ为随机的扰动强度，γW(t)代表了电压的随机扰动项，即U(t)可以看作为确定性谐和激励的频率Ω受到了扰动强度为γW(t)的随机扰动。

文中研究窄带随机过程中的Winner随机过程，Winner过程在应用中为标准信号，包含了γ=0单频激励。应用改进多尺度法研究γ≥0远小于1时的情形。多尺度法分析随机窄带噪声激励下的响应问题，已有一些成果[12–13]。所以式（3）变为

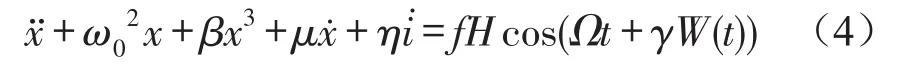
2 窄带激励主共振分析

引入非小量参数ε

将式（8）、式（9）代入式（5）后，同时对比α同次幂的系数，并对α0方程设解带入到α1的方程中，根据消除长期项的条件，分离实虚部可得

假设γ=0，则式（10）变为

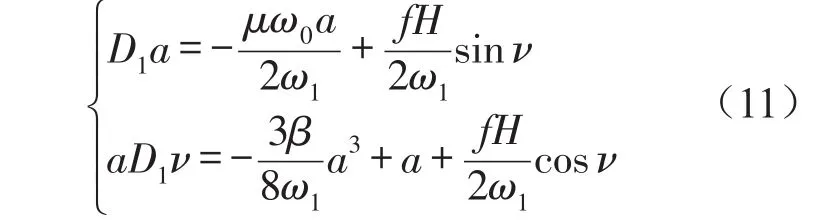
对于稳态振动a=a0，ν=ν0，有D1a=D1ν=0。得系统（11）的幅频响应方程

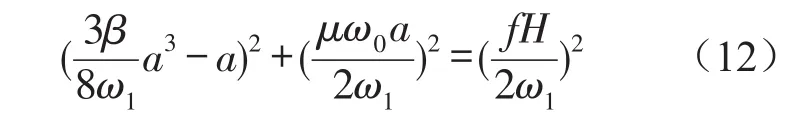
当γ≠0时，由于γ很小，可设方程（10）的解为

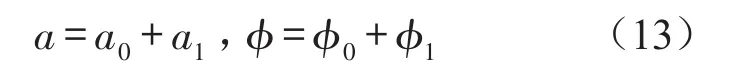
对于稳态振动a=a0，ν=ν0，有D1a=D1ν=0。代入式（11）可以得到a0和φ0，其中a1和φ1是摄动项，把式（13）代入式（10）中，不计关于a1和φ1的高阶项，便得方程（11）在点（a0，φ0）的线性方程为

依据Hurwitz[14]定理可知，该线性系统稳定的必要条件为

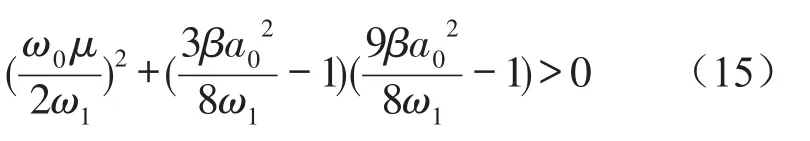
方程（14）可写成对应的Ito微分方程

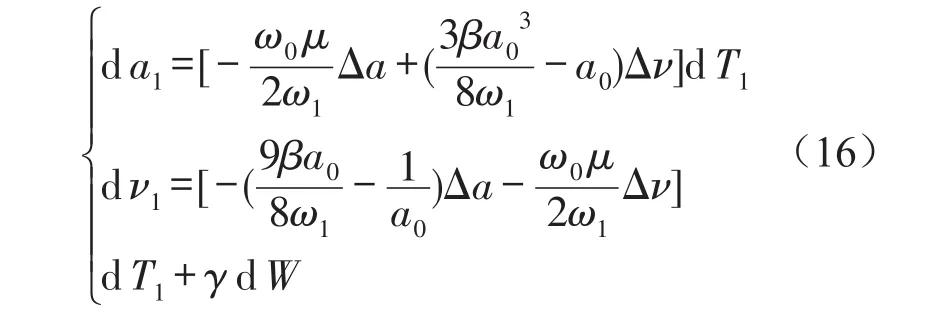
可用矩法[14]求出式（19）的1阶矩为

式（16）可写成如下形式

以下各式中Q1、Q2和Q3同上。

由Ito微分法则可得

则方程（19）可转化为

根据式（21）的系数矩阵，则

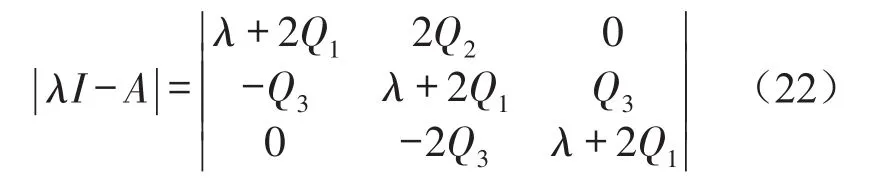
式（22）的特征方程为

式（25）即为2阶矩存在的充分必要条件，并与前面确定性系统周期解得稳定性条件是一致的。a0的值与Ea2的值是相互对应的。

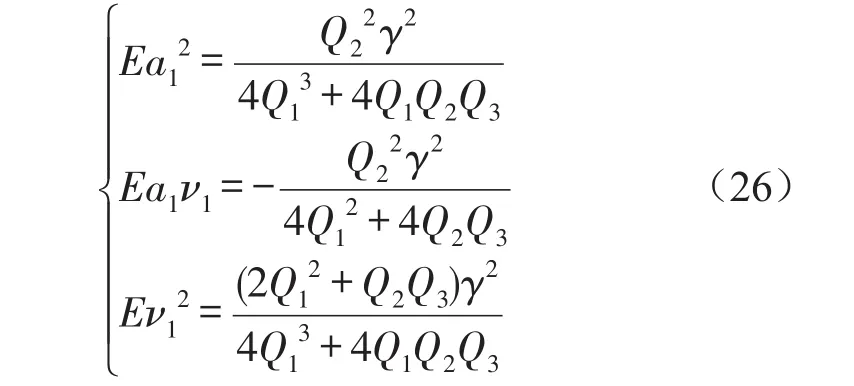
结合式（13）、式（17）、式（26）可得

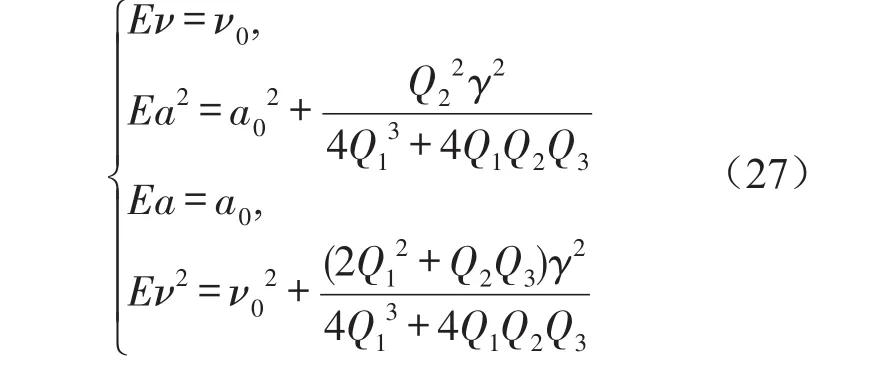
3 数值模拟

图2为电磁开关系统的幅频响应曲线，方程（5）中βx3项与项系数进行比较β相对较大，属于强非线性问题。由图2可知，当系统产生共振时振幅达到8 mm左右，电磁开关系统的间隙较大，符合工况要求。当电磁开关系统的间隙小于8 mm时，不符合工况要求，可以通过修改系统参数减小振幅，也可以在对电磁开关系统进行参数设计时避开固有频率与外激频率相等以减小振幅。

图3至图7为电磁开关系统主共振的均方响应曲线。其中实线部分为稳定解，虚线部分为不稳定解。

对比图2和图3，可得窄带随机激励下主共振系统均方响应曲线与γ=0时主共振系统幅频响应曲线的拓扑结构相同。

图3为电磁开关系统主共振随阻尼系数rv变化的均方响应曲线，由图3可知，增大线圈与磁铁之间的摩擦阻力系数，均方值减小。

图4、图5为电磁开关系统主共振随激励电压U0和Um变化的均方响应曲线，由图4、图5可知，随着激励电压U0、Um的增大，均方值增大。

图6、图7为电磁开关系统主共振随电阻r和R变化的均方响应曲线，由图6、图7可知，随着电阻r和R的增大，均方值减小。

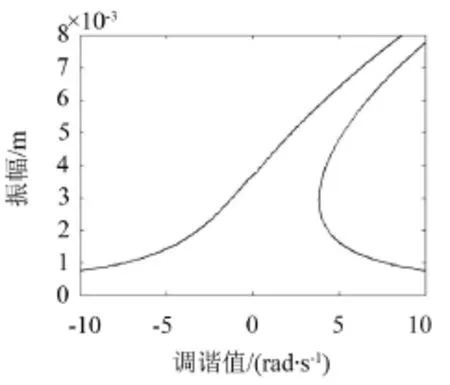
图2 幅频响应曲线

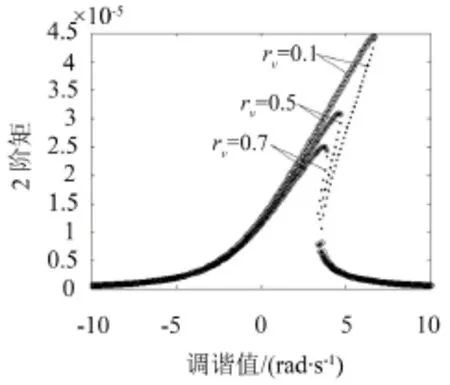
图3 均方响应曲线

图4 均方响应曲线

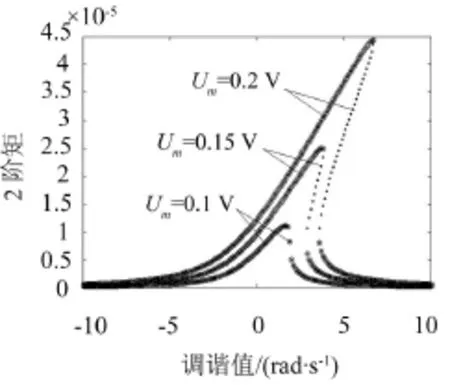
图5 均方响应曲线

图6 均方响应曲线

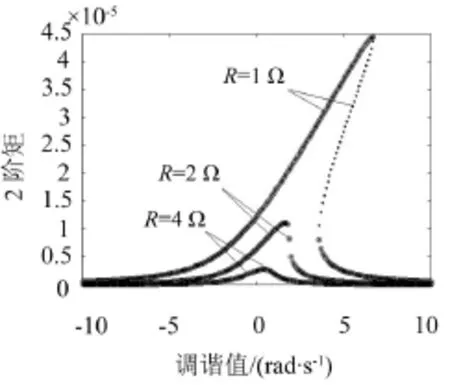
图7 均方响应曲线

4 主共振时间历程分析

用4阶龙格-库塔法计算出系统（8）的时间响应曲线和相图。

图8－图11为γ=0.01、γ=0.05时电磁开关系统主共振时间响应曲线。图9，11分别为γ=0.01、γ=0.05时电磁开关系统主共振相图。对比图8和10，图9和11可知，当γ变化时电磁开关系统的时间响应曲线和极限环变化不大。

5 结语

根据拉格朗日-麦克斯韦方程建立电磁开关系统动力学模型。应用改进多尺度法研究电磁开关强非线性系统主共振在窄带随机激励下的响应，得到系统主共振的幅频响应方程和随机均方响应的近似表达式，考虑了随机项对电磁开关系统响应的影响。结果表明，当系统产生共振时振幅达到8 mm左右，当电磁开关系统的间隙较大时符合工况要求。当电磁开关系统的间隙小于8 mm时，不符合工况要求，可以通过修改系统参数减小振幅，也可以在对电磁开关系统进行参数设计时使固有频率与外激频率避开以减小振幅。随着阻尼系数的增大，系统的均方值减小；随着激励电压幅值增大，系统的均方值增大；随着电阻增大，系统的均方值减小。通过改变电磁开关系统参数，得到系统均方响应曲线的变化规律，找到了振动的控制策略。

图8 γ=0.01时间响应曲线

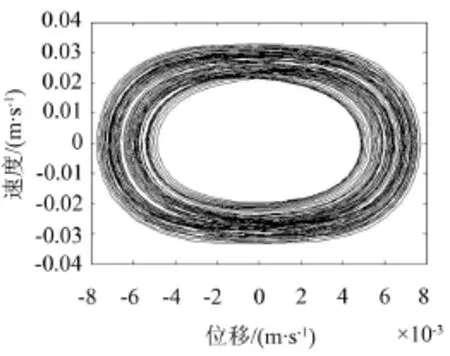
图9 γ=0.01的相图

图10 γ=0.05时间响应曲线

图11 γ=0.05的相图图9

[1]于成伟，马秀艳.起动机用电磁开关[J].汽车电器，2009 (2)：29-33.

[2]张胜川，边建华.汽车起动机电磁开关触片触点烧蚀原因探析[J].汽车电器，2010(4)：28-30.

[3]黄文锋.起动机电磁开关的结构改进[J].机电工程技术，2014(8)：130-131.

[4]杨志安，催一辉.非线性电阻电感型RLC串联电路主共振分析[J].天津大学学报，2007，40(5)：579-583.

[5]杨志安，李熙，孟佳佳.改进多尺度法求解环形极板机电耦合强非线性系统主共振的研究[J].振动与冲击，2015，34(19)：208-212.

[6]戎海武，孟光，王向东，等.窄带随机噪声作用下强非线性系统的响应[J].振动工程学报，2003，16(1)：81-84.

[7]关卓怀，蔡敢为.转子弯扭耦合振动共振特征分析[J].噪声与振动控制，2016，36(1)：5-10.

[8]韩修品，蒋丰.具有非线性减振器的弹性双层隔振系统建模[J].噪声与振动控制，2016，36(2)：31-34.

[9]DI LIUA,JING LIB,YONG XUC.Principal resonance responsesofSDOF systemswith smallfractional derivative damping under narrow-band random parametric excitation[J].Commun Nonlinear,2014,19(10):3642-3652.

[10]FENG Z H,LAN X J,ZHU X D.Explanation on the importance of narrow-band random excitation characters in the response of a cantilever beam[J].Journal of Sound and Vibration.2009,325(4):923-937.

[11]YANG ZHIAN,LI WENLAN,QIU JIAJUN.Lagrangemaxwellequationsand parameterresonanceofthe generator under magnetic saturation[J].Applied Mathematics and Mechanics,2007,28(11):1379-1386.

[12]DAVIS H G,LIU Q.The response probability density function of a Duffing oscillator with random narrow band excitation[J].Journal of Sound and Vibration,1990, 139:1-8.

[13]HUANG Z L,ZHU W Q,NI Y Q,et al.Stochastic averaging of strongly non-linear oscillators under bound-ed noise excitation[J].Journal of Sound and Vibration,2002,25（4）:245-267.

[14]朱位秋.随机振动[M].北京：科学出版社，1992.

Analysis of Primary Resonance of Nonlinear Vibration of Solenoid Switch Systems under Narrow-band Excitation

YANG Zhi-an1,ZHAO Li-sha2
(1.Key Laboratory of Structure and Vibration Engineering of Tangshan,Tangshan College, Tangshan 063000,Hebei China; 2.School of Mechanical Engineering,North China University of Technology, Tangshan 063000,Hebei China)

The strong nonlinear vibration of the electric circuit and magnetic circuit coupled solenoid switch system under narrow-band excitation is investigated.The stochastic differential equation of the solenoid switch system subjected to narrow-band excitation is established.The frequency response equation of the system is obtained based on the modified multi-scale method.The stability of the primary resonance of the system is calculated.And the influence of the parameters of the system on the mean square value of the primary resonance of the system is analyzed.The results show that the mean square value of the primary resonance of the system reduces with the increasing of the damping coefficient,increases with the increasing of the excitation voltage amplitude,and reduces with the increasing of the resistance.The change of limit cycle of the system is small with the increasing of the intensity of the random disturbance.

vibration and wave;solenoid switch;the modified method of multiple scales;narrow-band random excitation;mean square value;strongly nonlinear vibration

0324

：ADOI编码：10.3969/j.issn.1006-1335.2017.01.007

1006-1355(2017)01-0030-05

2016-05-05

河北省自然科学基金项目资助（A200900097）

杨志安（1963－），男，河北省秦皇岛市人，博士，教授，硕士生导师，研究方向为机构学与机械动力学。E-mail:yangzhi_an@163.com

赵利沙（1988－），女，河北省邯郸市人，硕士研究生，研究方向为机构学与机械动力学。E-mail:948281620@qq.com