线性阻尼杆振动问题基于变量变换的多辛算法

鲍四元，邓子辰

（1.苏州科技大学 土木工程学院，江苏 苏州 215011；2.西北工业大学 工程力学系，西安 710072）

线性阻尼杆振动问题基于变量变换的多辛算法

鲍四元1，邓子辰2

（1.苏州科技大学 土木工程学院，江苏 苏州 215011；2.西北工业大学 工程力学系，西安 710072）

提出线性阻尼杆振动问题基于变量变换的多辛离散算法。首先通过变量变换把耗散系统化为保守系统。其次以变换变量组成状态向量并采用中点离散方法构造中点Box多辛离散格式，然后，基于空间层的状态变量建立矩阵形式的递推关系，最后结合空间边界条件和初始条件建立线性方程组求解。研究结果表明，构造的多辛算法不仅能够保持系统守恒型几何性质，通过状态变量合理表示了边界条件，而且能够较准确地体现系统的耗散效应。

振动与波；变量变换；多辛；保结构；耗散

作为保结构算法的奠基人，冯康先生敏锐地觉察到数值算法构造过程中算法在保持原系统固有几何性质方面具有重要的性能，并于1984年在双微国际会议上提出了基于辛几何原理的辛算法［1］，用于解决有限维Hamilton体系数值求解过程中的保结构问题。保结构算法的基本出发点是使得数值离散尽可能与原连续系统保持在统一框架下，即尽可能多地保持系统的固有几何性质。自此，冯康先生开辟了保结构算法研究的新领域，至今国内外学者在辛算法方面取得了重大而丰富的研究成果[1–5]。

在多年的研究过程中，辛算法的一个不足之处在于空间依赖的连续系统并不能采用辛算法进行数值求解。因此，Bridges教授在辛算法的基础上，针对无穷维Hamilton系统提出了多辛算法［6］，用以在数值求解过程中保持系统的局部几何性质。最近，多辛算法在动力学方面得到不少应用和发展[2，7–9]。

实际的力学系统往往要考虑耗散效应，耗散效应的存在破坏了系统的多辛对称性。近年来，胡伟鹏教授和邓子辰教授针对耗散Hamilton系统，提出了广义多辛算法［10］，将保结构算法理论体系拓宽至耗散系统，从而突破了多辛算法的一个“瓶颈”，但广义多辛算法存在一定的近似和误差。

变量变换是力学中重要理论和方法。例如，在振动问题的研究中，变量变换能够将耦合振动解耦，分离成无耦合的简正振动[11]。文献[12]引入了三类含时的变量变换，将阻尼谐振子(DHO)中的阻尼从形式上消除，变换成简谐振子(SHO)。

本文基于变量变换的方法，把阻尼项从杆振动微分方程中形式上消去，使得以新变量表示的振动微分系统是保守的，从而在多辛理论框架下，采用多辛算法研究了大阻尼杆的振动特性，即首先通过正则变换，构造杆振动控制方程的广义多辛形式，并研究多辛形式中的数学表述。其次，采用中点离散方法离散多辛形式，构造其中点Box广义多辛离散格式；随后利用该格式求解，模拟阻尼杆的振动，最后研究振动过程中的阻尼耗散效应。本文的研究相对于广义多辛算法而言，采用变量变换把耗散系统转化为保守系统，因此精度更高，将进一步完善保结构算法的理论体系，同时为耗散动力学系统的数值求解提供新的途径。

1 阻尼杆振动方程基于变换变量的的多辛形式

由于材料本构关系中含有阻尼项，杆件的振动需要考虑阻尼。单位长度悬臂阻尼杆的一维自由振动控制方程可以表述如下

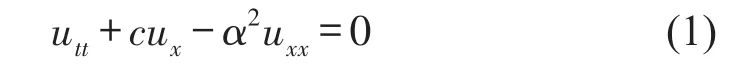
其中u是纵向位移，α是纵向应力波的传递速度，c为不可忽略的阻尼系数，由于阻尼项的存在，杆振动振幅将会逐渐减小，常规的数值算法难以得到精确的衰减速度和振动时间。为了把系统变换为保守的，消去微分方程中的阻尼项，把式（1）改写为

式（3）代入式（2），化简得

式（4）中不再含U的1阶偏导数，故易于写成多辛形式。引入新变量和正交变换：V=Ut，W=Ux，得到与式（4）等价的多辛方程组形式为

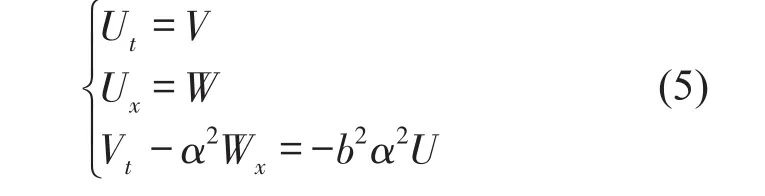
式（5）可写为Hamilton体系下的1阶形式

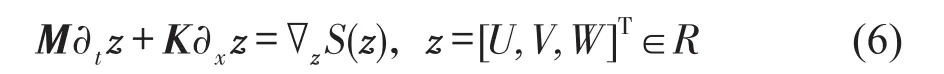
其中Hamilton函数为

多辛算法的特色在于其满足三种基本的守恒律，即：多辛守恒律、局部能量守恒律和局部动量守恒律。这也是多辛形式的优势所在。

2 基于变换新变量的多辛离散

中心差分法是最简单的差分离散方法，在构造多辛格式时也最简单，计算量最小。本文选取空间方向的步长为h，空间方向节点数为m，对应于i=1，2，…，m；时间方向的步长为τ，时间方向节点数为n，对应于j=1，2，……，n。对计算区域进行均匀划分，状态变量z在(xi,tj)网格点上的值记为对式（5）在空间和时间方向上分别用中点差分离散法近似，得到方程（5）的中点Box格式为

其中部分符号的含义如下

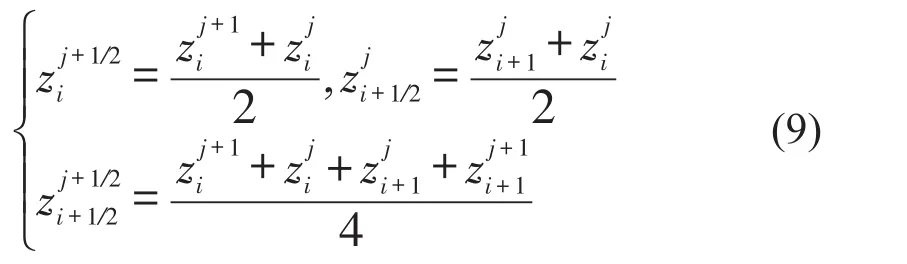
式（9）中z表示新变量U、V和W。故式（8）可写为

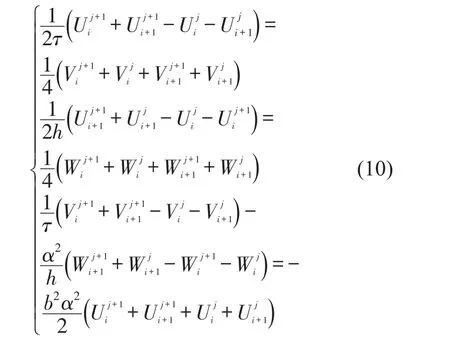
其中i=1，2，……，m-1。

空间上杆左右两端处均有边界条件，宜对建立的中点Box广义多辛格式在空间层上用矩阵表示。格式（10）可写成如下的向量形式

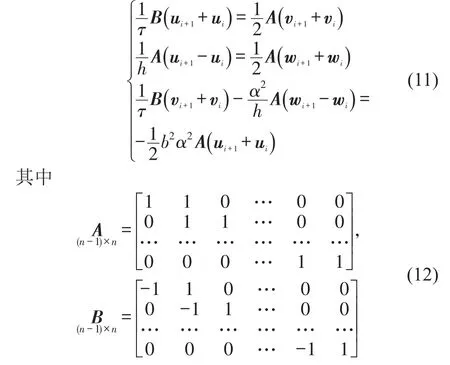
式（12）矩阵下方的标注表示该矩阵的维数。而式（11）中i取不同值汇总后可化为如下矩阵形式

式（13）反映了不同空间层上状态向量的迭代关系，图1给出辅助直观的理解，可由图1中相邻竖直线上的状态向量的迭代体现。

图1 空间层上的状态变量迭代法示意图（i对应于空间，j对应于时间变量）

由式（13），当l取不同值所得式子汇总后写成矩阵 形 式 ，令记则得矩阵形式的线性方程组

其中R是块三对角矩阵，以块形式表示时维数是(m-1)×m，代入矩阵P、Q展开后的实际维数是3(m-1) (n-1)×3 mn。

方程（15）的Y向量含3 mn个待定元素，而矩阵R的行数为3(m-1)(n-1)小于3 mn。因此需结合初始条件和边界条件求解出全部未知量。实际问题中可调节参数m和n的值，使得方程（15）可解。

3 初始条件和边界条件的变换

利用方程（15）求解杆振动问题时，需考虑边界条件和初始条件。但式（3）变换了位移变量，故边界条件和初始条件需采用变换后的新变量表示。

对于零初始条件，一般采用新变量仍表示为零初始条件。

杆的空间约束包括自由端和固定端两种。若约束是自由端，其边界条件为把式（3）代入化简得

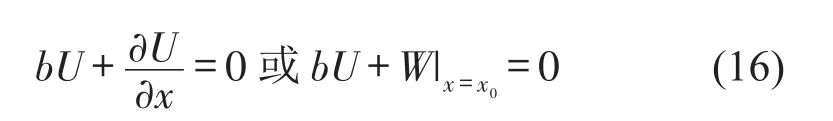
若约束是固定端，其边界条件为u(x,t)=0，代入式（3）得

对于给定的位移初始或力初始条件，也可根据式（3）得到新变量表示的形式。

4 数值实验

以一端固定一端自由的悬臂均匀杆为例，其他约束可类似研究。杆振动控制方程仍为式（1），受初始位移（或外力）边界条件。设杆长为1，参数α=1，阻尼系数c=0,2和4。杆的空间约束边界条件如下

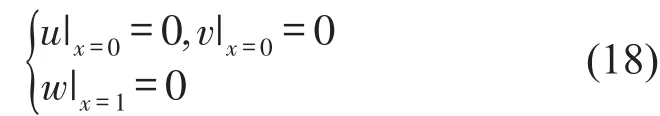
同时给定自由端单位纵向位移作为初值条件

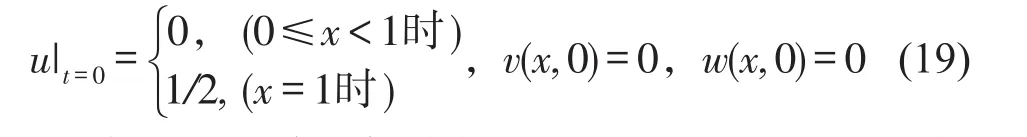
本例属于给定初值的自由振动问题，但不易得到精确解。

按式（16），边界条件式（18）变换为

图2 不同m，n值所得自由端位移随时间变化图

图2中，(m，n)分别取(11，13)、(17，19)和(23，25)时，自由端的位移均逐渐衰减，而三者中取(11，13)时误差相对大一些，尤其后半段时间位移出现波动，实际上后部分的位移可由平滑处理或拟合趋近为零。一般认为，图1的计算网格越细，结果应更准确一些，即图2（c）的结果相对更准确。

阻尼系数c对杆自由端位移的影响也反映在图2中。阻尼系数大时，自由端位移衰减得更快。另外，图3和图4给出不同阻尼系数时杆中点的位移和应变变化，其中参数m取16，n取18。

图3 杆中点的位移变化（m=16，n=18）

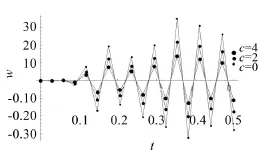
图4 杆中点的应变变化（m=16，n=18）

5 结语

本文给出了线性阻尼杆振动基于变量变换的多辛算法。所提算法满足多辛算法的多辛守恒律、局部能量守恒律和局部动量守恒律。计算最终转换为针对线性方程组求解出所有状态变量，通过变量变换描述线性阻尼引起的耗散，即表述阻尼时未采用近似，从而更好地模拟并解决了实际问题。

所提方法对于某些类似的非保守系统的多辛算法具有重要的借鉴意义。

[1]冯康，秦孟兆.哈密尔顿系统的辛几何算法[M].杭州：浙江科学技术出版社，2003

[2]秦孟兆，王雨顺.偏微分方程中的保结构算法[M].杭州：浙江科技出版社，2011.

[3]钟万勰.力、功、能量与辛数学[M].大连：大连理工大学出版社，2007.

[4]钟万勰，辛破茧.辛拓展新层次[M].大连：大连理工大学出版社，2011.

[5]YAO WEIAN,ZHONG WANXIE.Symplectic elasticity [M].Singerpore:world scientific press,2009.

[6]BRIDGES T J.Multi-symplectic structures and wave propagation[J].MathematicalProceedingsofthe Cambridge Philosophical Society,1997,121(1):147-190.

[7]胡伟鹏，邓子辰.无限维动力学系统的保结构分析方法[M].西安：西北工业大学出版社，2015.

[8]HU W P,HAN S M,DENG Z C,et al.Analyzing dynamic response of non-homogeneous string fixed at both ends[J].International Journal of Non-Linear Mechanics,2012, 47(10):1111-1115.

[9]王俊杰.弹性波方程的多辛Preissmann格式计算[J].地球物理学进展，2014，29(4)：1758-1765.

[10]胡伟鹏，邓子辰.大阻尼杆振动的广义多辛算法[J].动力学与控制学报，2013，11(1)：1-4.

[11]丁光涛.阻尼谐振子的拉格朗日函数和哈密顿函数[J].大学物理，2009，28(5)：13-14.

[12]丁光涛.阻尼谐振子到简谐振子的变换[J].大学物理，2013，32(1)：1，17.

[13]钟万勰.应用力学的辛数学方法[M].北京：高等教育出版社，2006.

Multi-symplecticAlgorithm for VibrationAnalysis of the Rods with Linear Damping

BAO Si-yuan1,DENG Zi-chen2
(1.School of Civil Engineering,University of Science and Technology of Suzhou, Suzhou 215011,Jiangsu China; 2.Department of Engineering Mechanics,Northwestern Polytechnic University,Xi’an 710072,China)

The discrete multi-symplectic alogrithim for vibration problem analysis of the rods with linear damping is proposed.First of all,the dissipation system is transformed into a conservative system by variable transformation.Then,the state vector is formed by the transformed variables,and the midpoint box multi-symplectic form is generated based on the midpoint discrete method.Finally,the matrix-type recurrence formula is established based on the state vector and the linear equation set including the boundary condition and the initial condition is formed and solved.The numerical results show that the proposed multi-symplectic algorithm can reserve the conservative geometrical properties of the system,reasonably express the boundary condition by the state variables,and accurately reflect the dissipation effect of the system.

vibration and wave;variable transformation;multi-symplectic;structure-preserving;dissipation

O326；O422.6

：A

：10.3969/j.issn.1006-1335.2017.01.004

1006-1355(2017)01-0016-04

2016-08-26

国家自然科学基金资助项目（11202146）

鲍四元（1980－），男，安徽省六安市人，博士，副教授，研究方向为非线性动力学及计算。

邓子辰，男，博士生导师，长江学者。E-mail:dweifan@nwpu.edu.cn