火炮后坐对膛口流场的影响*
2017-02-28雷红霞王志军
雷红霞, 王志军
(中北大学 机电工程学院, 山西 太原 030051)
火炮后坐对膛口流场的影响*
雷红霞, 王志军
(中北大学 机电工程学院, 山西 太原 030051)
针对国内外有关膛口流场的研究现状, 基于计算流体力学理论, 研究了火炮后坐运动对膛口流场的影响. 采用轴对称Euler方程组和有限体积法( FVM ), 建立了某火炮有、 无后坐运动两种情况下的膛口流场数值计算模型; 利用计算流体力学软件和动网格技术,分别对其进行了非稳态数值模拟; 通过对火炮在有、 无后坐时膛口流场的数值模拟结果进行对比, 分析了火炮后坐对膛口流场的影响. 研究表明: 火炮后坐运动时膛口前方的压力降低, 膛口后方的压力增大; 火炮后坐对炮膛合力产生的影响较小.
膛口流场; 动网格; 非稳态流动; 火炮
0 引 言
在火炮发射过程中, 弹丸飞出炮口瞬间, 膛内高温、 高压的火药气体被突然释放, 向炮口外高速喷射、 急剧膨胀, 形成非常复杂的膛口流场, 所产生的冲击波会对周围的人员和设备产生危害[1]. 近年来, 随着CFD技术的发展, 国内外对膛口流场进行了大量实验和数值研究. 郭则庆等分别对膛口初始流场及其对火药燃气流场的影响进行了研究, 对后效期火药气体的流空过程进行了分析, 对有弹丸时不同制退器的膛口流场波系结构进行了数值计算和研究[2-4]. Biss对膛口的冲击波进行了高速摄影, 研究了冲击波的传播规律; Cler将CFD应用到膛口流场计算并进行了验证[5-6]. 以上工作均是在炮身静止的前提下进行的研究. 对于考虑火炮后坐时的膛口流场结构的相关文献, 目前国内外并没有看到.
为了研究火炮后坐对膛口流场结构的影响, 本文以122 mm榴弹炮为研究对象, 采用计算流体力学结合动网格技术, 建立了膛口流场数值计算模型, 利用轴对称Euler方程组和有限体积法, 对膛口流场进行了非稳态数值模拟, 得到了火炮在有、 无炮身后坐时膛口流场的发展过程, 并比较了两种情况下膛口周围压力的变化, 分析了炮身后坐对膛口流场的影响.
1 数值分析
1.1 流体的运动控制方程
由于身管内部结构为对称形状, 因此, 为了减小计算量, 提高计算效率, 本文采用的是二维轴对称模型. 忽略化学反应和多相流的影响, 非定常可压缩理想气体的Euler方程满足
(1)
式中:U=[ρ,ρu,ρv,ρE]T;F=[ρu,(ρu2+p),ρuv,(ρE+p)u]T;G=[ρv,ρuv,(ρv2+p),(ρE+p)v]T;ρ为气体密度;u,v分别为x,y方向的速度分量;E为单位质量气体的总能量, 其表达式为
(2)
式中:r为理想气体绝热指数.
理想气体的状态方程为
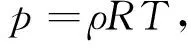
(3)
式中:R是通用气体常数.
方程(1)~(3)组成了封闭的方程组.
1.2 弹丸运动方程
弹丸的运动方程由牛顿第二定律得出, 弹丸的速度方程为
(4)
式中:vi为某时刻弹丸的运动速度;vi-1为前一时刻弹丸的运动速度;F1为本时刻弹底受力;F2为本时刻弹前空气阻力, 由流场计算结果得到;m为弹丸质量m=22 kg; Δt为时间步长, Δt=5 μs.
1.3 炮身的运动方程
控制炮身运动的方程满足牛顿第二定律, 后坐速度方程为
(5)
式中:vj为某时刻身管的后坐速度;vj-1为前一时刻身管的后坐速度;Fptj为本时刻的炮膛合力, 由流场计算结果得到;FRj为本时刻后坐阻力为常数, 由给定第二类后坐制动图得到为15 230 kg;M为后坐部分质量,M=1 300 kg; Δt为时间步长, Δt=5 μs.
1.4 离散方法及计算格式
本文采用有限体积法, 时间推进采用二阶Runge-Kutta法, 对流项选用能在较大马赫数下提高对激波等间断面捕捉效率的AUSM格式进行求解.
1.5 计算模型及动网格方法
本文主要是对后效期身管后坐对流场结构的影响进行研究, 122 mm榴弹炮不带制退器的计算域如图 1 所示. 图 1(a)为不考虑后坐的计算模型, 将计算区域分为2个区域: A区域和B区域. A区域和B区域通过膛口端面来分割; 图1(b)为考虑身管后坐的计算模型, 将计算区域分为3个区域: A、 B和C区域. 其中, A区域和B区域通过膛口端面来分割, B区域和C区域通过运动分界面来分割, 运动区域和静止区域的数据交换是通过插值的方式实现的. 计算过程中弹丸的运动速度和炮身的后坐速度分别由式(4)和(5)得到.

图 1 计算域示意图Fig.1 Calculation models
由内弹道计算得到的结果对身管内各物理量分布进行初始化, 其压力、 速度和温度分布如图 2 所示. 膛内火药气体的平均密度为95.4 kg/m3, 火药气体相对分子量为22.97, 比热比为1.23. 两种模型的计算区域大小相同, 其中外部区域取长12 000 mm, 宽10 000 mm的长方形. 在本计算中, 为了避免采用非结构网格带来过多的格式耗散, 本文的计算区域全部采用结构网格, 网格数量为23万左右.
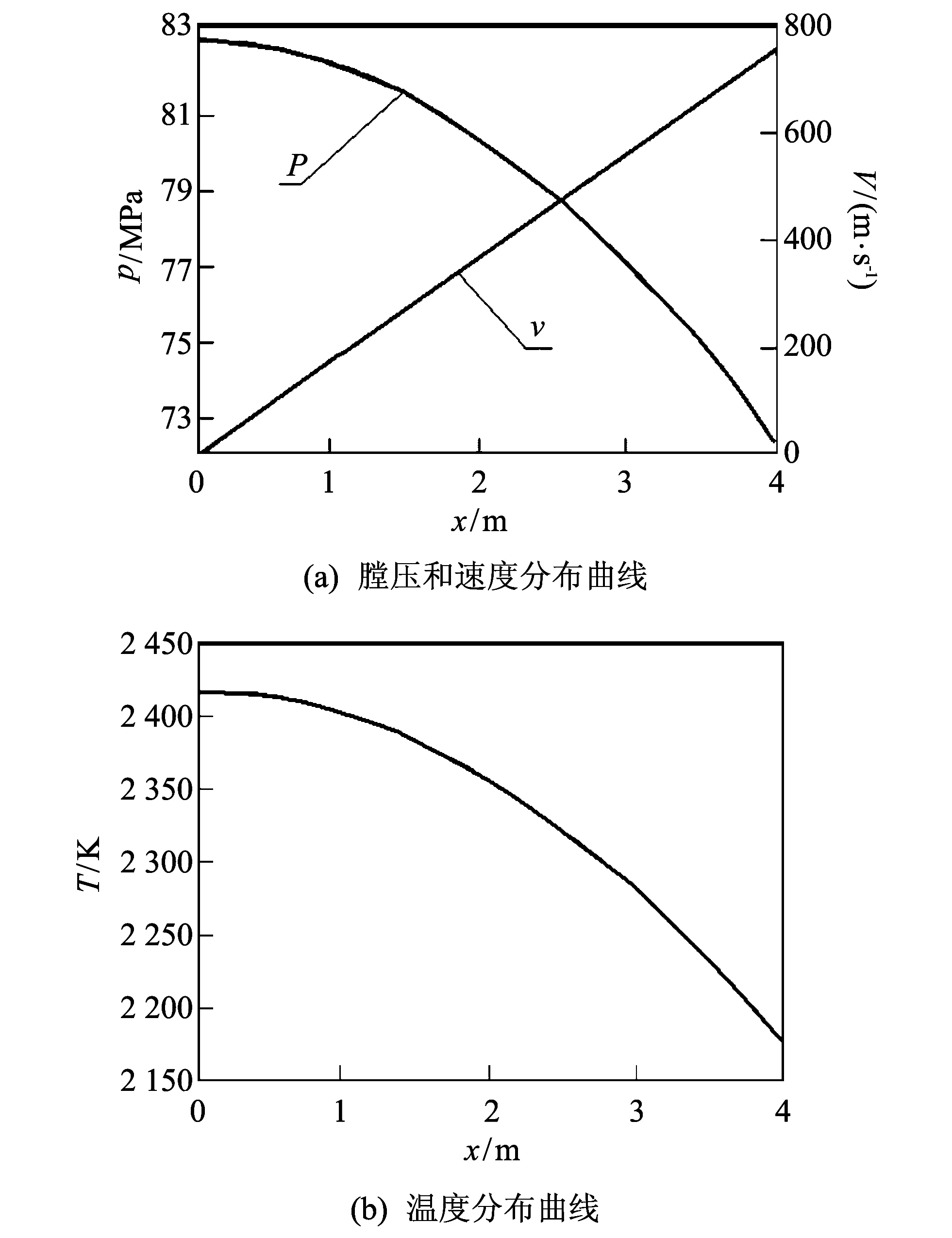
图 2 初始条件Fig.2 Initial conditions
由于本文研究炮身后坐对流场结构的影响, 而炮身后坐会引起网格的变形, 因此本文的网格采用了动网格技术. 由于只考虑炮身沿轴线方向的平移, 所以本文采用动态网格层变法. 动态层变法是在与运动边界相邻处的结构化网格区域, 根据运动规律动态的增加或减少网格层数, 以此来更新区域的网格的方法. 增加网格或减少网格依据的是运动边界相邻网格的高度, 如果临近边界层网格高度超出了所指定的网格的尺寸, 就将其划分为两个网格层; 如果网格层高度小于所规定的网格尺寸, 就将紧邻边界的两层网格合并为一层网格, 网格的分割与合并是通过插值方法实现的[7-10].
1.6 计算方法验证
为了验证二维轴对称后坐模型的正确性, 对考虑后坐时后坐速度随时间的变化与理论后坐速度随时间的变化进行了对比, 如图 3 所示. 从图中可以看出, 在开始阶段理论计算的后坐速度要大于流场的计算结果, 但是大约5 ms以后, 理论计算结果下降速度大于流场计算结果, 在最后的时刻流场计算结果大于理论计算结果. 理论计算最大后坐速度出现在2.9 ms为12.779 4 m/s, 流场计算的最大后坐速度出现在3.1 ms为12.722 6 m/s, 误差为0.5%. 在后效期结束的时刻理论计算后坐速度为7.206 m/s, 流场计算结果为7.346 m/s, 相差1.9%. 上述结果验证了所用计算模型的准确性, 可以满足工程计算.
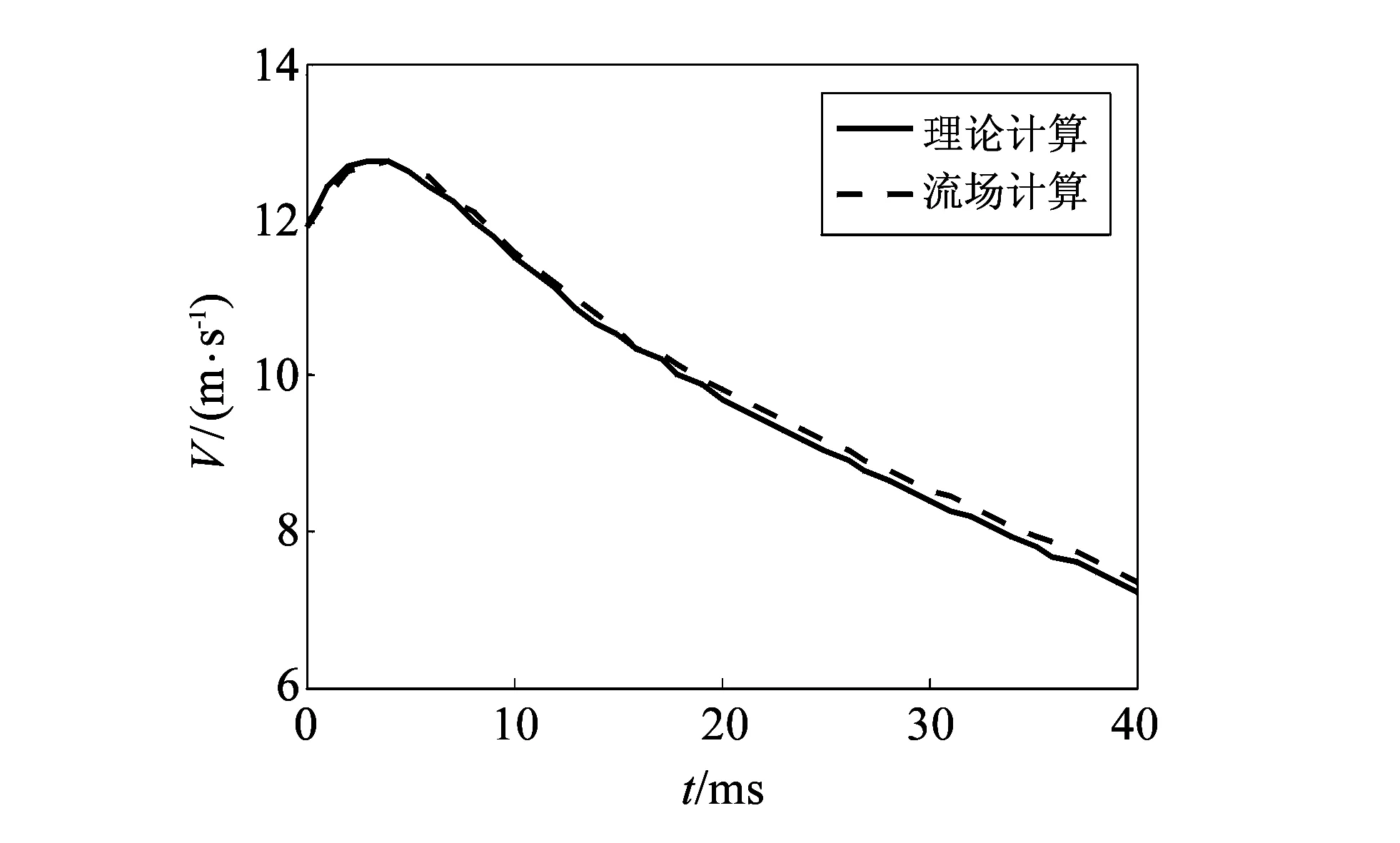
图 3 后坐速度随时间的变化曲线Fig.3 Curve of recoil velocity changes with time
2 计算结果与分析
2.1 流场结构对比
火炮后坐主要是对膛口周围的流场产生影响, 为此通过对比图 4 中有、 无后坐的数值计算结果来分析后坐对膛口流场的影响. 以t=0时刻为后效期开始的时间, 不考虑初始流场的影响, 从计算的阴影照片可以看出, 计算结果清晰地显示出了非定常欠膨胀射流发展过程, 即以斜激波、 反射激波和马赫盘组成的瓶状激波系为特征的射流结构经历了生长、 稳定和衰减的过程.
不考虑火炮后坐时, 在后效期开始的初期, 由于弹丸的运动速度小于火药燃气的速度, 弹底出现弹底激波, 同时火药燃气在弹丸的侧方膨胀加速形成炮口射流和冲击波, 0.5 ms时射流角迅速扩张到最大; 随着火药气体从膛口不断地喷出, 冲击波在传播过程中遇到射流边界后形成了斜激波, 斜激波遇到马赫盘后发生反射, 形成反射激波, 于是在马赫盘的边缘与斜激波和反射激波交汇, 形成三叉激波, 2.5 ms时炮口处射流瓶状激波结构逐渐形成, 同时, 随着弹丸的向前运动, 在弹底形成尾迹, 并在弹前出现弹头激波; 在之后的5~7 ms内, 随着火药燃气射流的自由发展, 弹底激波消失, 激波瓶和马赫盘处于一个相对稳定的变化过程, 激波瓶外存在强烈的湍流混合区; 随着压力比的进一步下降, 10 ms时射流强度降低, 激波瓶和马赫盘的直径明显的减小, 瓶装激波结构过渡为X形周期性激波系. 由图 4 还可以看出, 在射流的衰减期内, 瓶状激波系的直径比其长度衰减的时刻要早, 当直径开始缩小之后, 其长度仍处于增长阶段或者稳定时期, 体现为瓶装激波系在后效期中不断的被拉长. 伴着膛口压力的变化, 激波瓶经历了由生长、 变大、 稳定和消亡的过程.
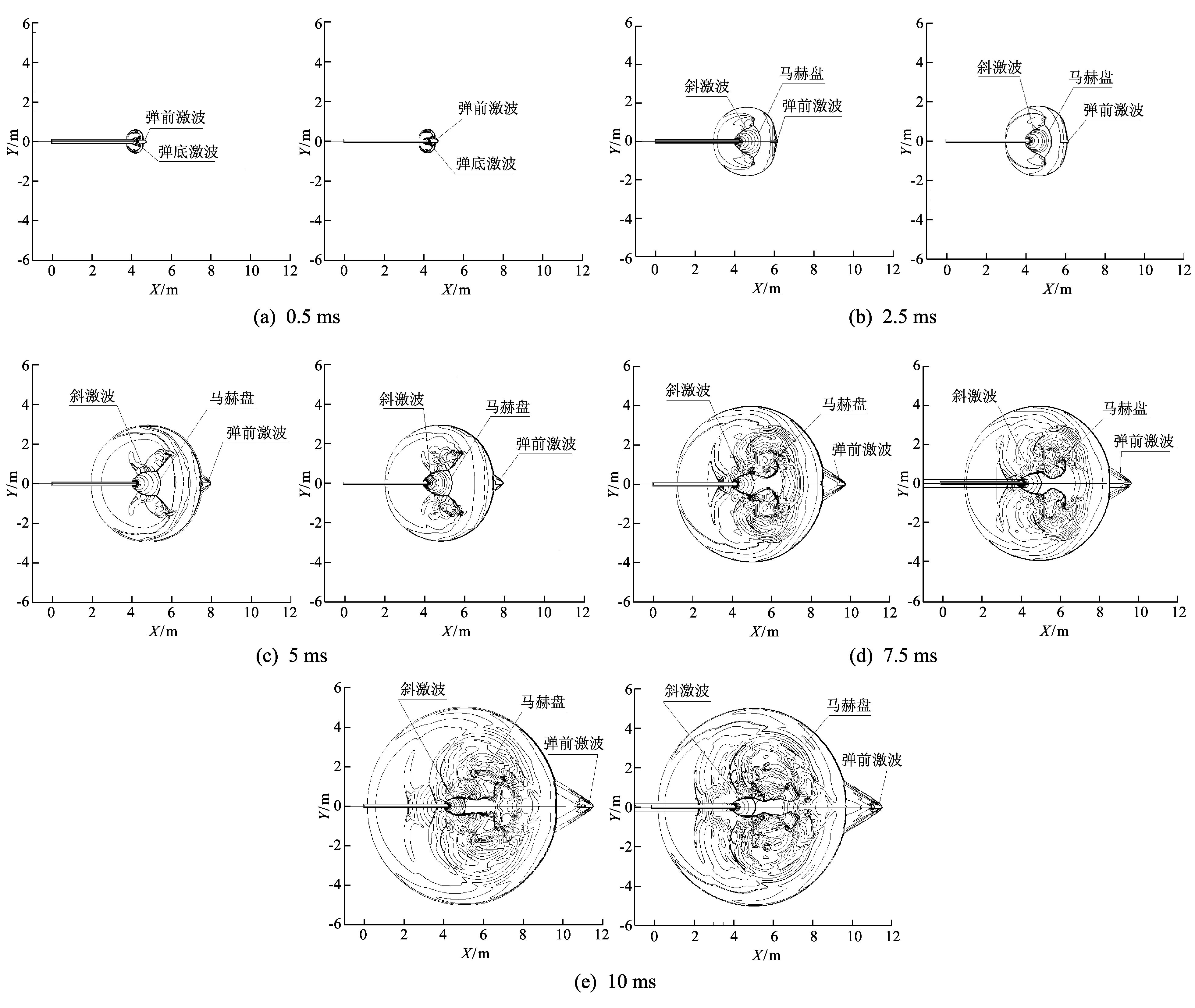
图 4 膛口流场计算阴影图Fig.4 Numerical schlieren images of muzzle flow
考虑火炮后坐时, 膛口流场的发展过程和不考虑火炮后坐时相差不大, 激波瓶经历了相似发展过程, 在流场结构云图上两者的变化不大, 对比结果不明显. 其原因是由于后坐时间相对于整个后效期时间非常短暂, 而且后坐位移相对于流场区域较小.
2.2 压力变化对比
为了进一步研究火炮后坐对膛口周围压力场的影响, 对膛口周围的多个点进行了压力监测, 两种模型检测点的位置是固定不变的, 监测点示意如图 5 所示. 图 6 给出监测点压力随时间的变化曲线. 表1给出各监测点总压的最大值.
由图 6 和表 1 可以看出, 两组数据中监测点的压力值都是随着角度的增加而逐渐减小的, 监测点最大压力值出现时刻随着角度的增加而推迟, 说明炮口冲击波的波阵面是近似为一球形且球心是运动的, 是一个各向异性的非均匀冲击波. 对比表1中考虑后坐和不考虑后坐监测点的压力数据可以发现, 在30°~90°之间时, 考虑后坐时的监测点的压力值低于不考虑后坐时监测点压力值, 在90°~150°之间时, 考虑后坐时的监测点压力值高于不考虑后坐时监测点的压力值; 其原因主要是炮身后坐, 后坐速度方向和炮口冲击波波阵面的运动方向相反, 而且考虑后坐时炮身的位移是随时间变化的, 这就造成了炮口和监测点位置之间距离的减小, 因而冲击波的强度要高于不考虑后坐时冲击波的强度. 通过表1中监测点的压力相对偏差绝对值可以看出, 炮口端面前方的偏差较大, 最大为8.31%, 炮口端面后方的偏差较小, 不到1%, 由此可以看出, 炮身后坐对炮口前方的影响较大, 对炮口后方的影响较小. 所以, 在对炮口后方超压值进行研究时, 可以忽略身管后坐对其压力场的影响.

图 5 监测点位置示意图Fig.5 Schematic diagram of monitoring points
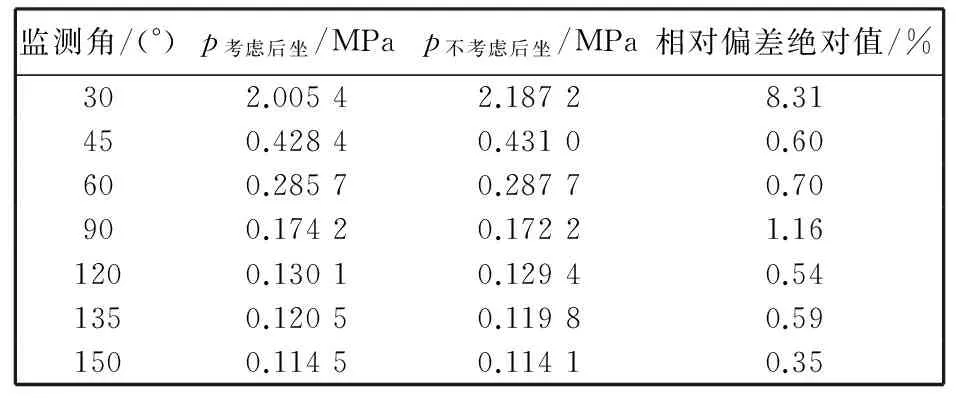
监测角/(°)p考虑后坐/MPap不考虑后坐/MPa相对偏差绝对值/%302.00542.18728.31450.42840.43100.60600.28570.28770.70900.17420.17221.161200.13010.12940.541350.12050.11980.591500.11450.11410.35
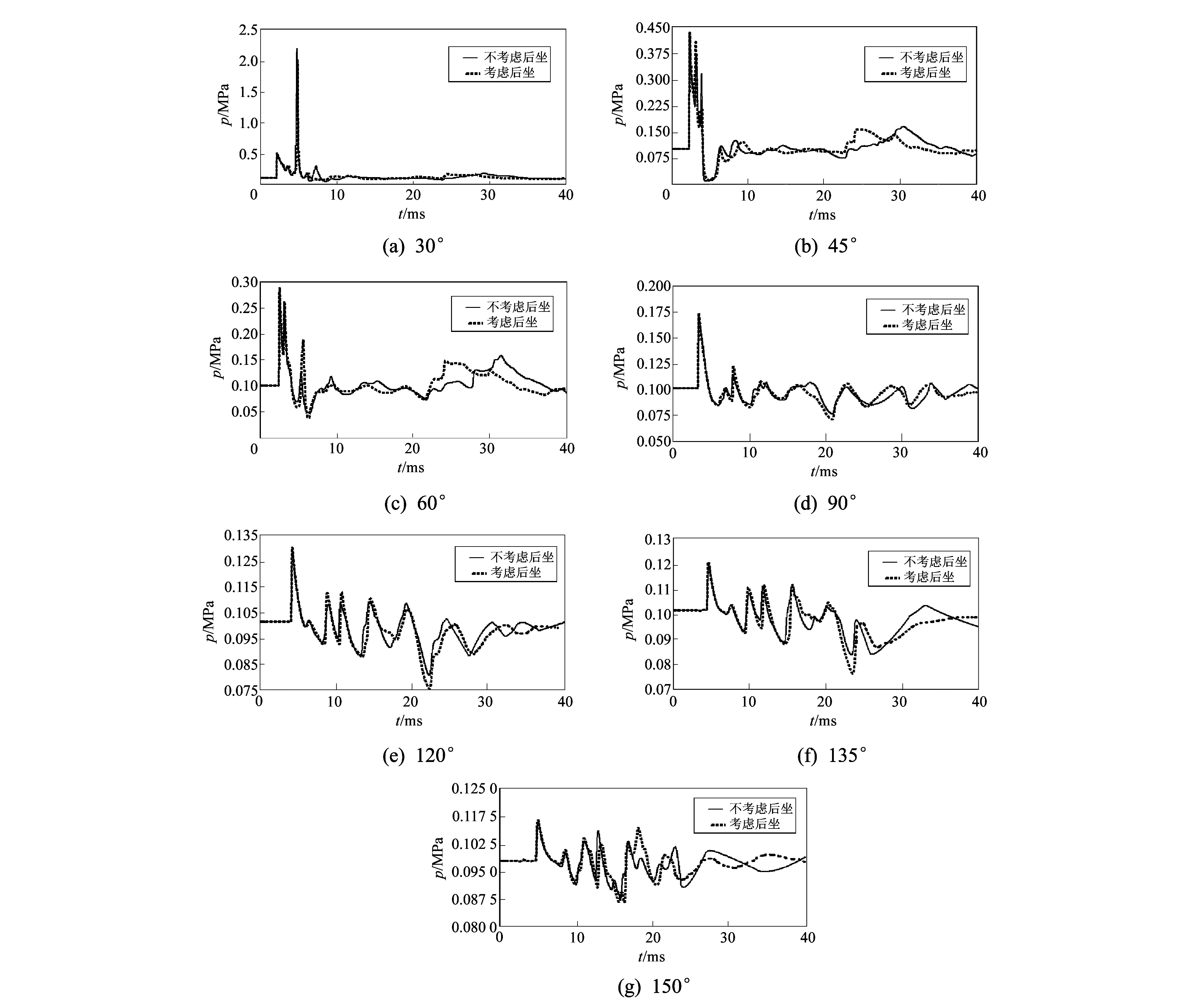
图 6 监测点压力随时间的变化曲线Fig.6 Pressure of monitoring points changes with time
3 结 论
本文通过火炮后坐时后坐速度的变化和理论计算的对比, 验证了所用计算方法的正确性和准确性, 进而对火炮后坐对流场结构的影响进行了研究, 通过计算得到以下结论:
1) 考虑后坐与不考虑后坐时的膛口流场结构变化不明显, 射流结构经历了生长、 稳定和衰减的变化过程;
2) 以炮口点为中间点, 考虑火炮后坐时炮口前方的压力低于不考虑后坐时的压力, 火炮后坐时炮口后方的压力大于无后坐时炮口后方的压力;
3) 在对炮口后方超压值进行研究时, 可以忽略身管后坐对其压力场的影响.
[1]苗瑞生. 发射气体动力学[M]. 北京: 国防工业出版社, 2006.
[2]郭则庆, 王杨, 姜孝海, 等. 膛口初始流场对火药燃气流场影响的数值研究[J]. 兵工学报, 2012, 33(6): 663-668. Guo Zeqing, Wang Yang, Jiang Xiaohai, et al. Numerical study on effects of precursor flow on muzzle propellant flow field[J]. Acta Armamentarii, 2012, 33(6): 663-668. (in Chinese)
[3]王杨, 郭则庆, 姜孝海. 后效期火药气体流空过程数值模拟[J]. 火炮发射与控制学报, 2009, 30(3): 63-67. Wang Yang, Guo Zeqing, Jiang Xiaohai. Numerical simulation of propellant gas emptying process In after-effectPeriod[J]. Journal of Gun Launch and Control, 2009, 30(3): 63-67. (in Chinese)
[4]张焕好, 陈志华, 姜孝海, 等. 高速弹丸穿越不同制退器时的膛口流场波系结构研究[J]. 兵工学报, 2012, 33(5): 623-629. Zhang Huanhao, Chen Zhihua, Jiang Xiao-hai, et al. Investigation on the blast wave structures of a high-speed projectile flying through different muzzle brakes[J]. Acta Armamentarii, 2012, 33(5): 623-629. (in Chinese)
[5]Biss M M, Settles G S, Hargather M J. High-speed digital shadowgraphy of shock waves from explosions and gunshots[J]. Shock Waves, 2009(2): 91-96.
[6]Cler D L, Chevaugeon N, Shephard M S, et al. CFD application to gun muzzle blast a validation case study, 2003-1142[R]. Nevada: AIAA, 2003.
[7]姜孝海, 范宝春, 李鸿志. 基于ALE 方程的动网格膛口流场数值研究[J]. 计算力学学报, 2008, 25(4): 563-567. Jiang Xiaohai, Fan Baochun, Li Hongzhi. Numerical investigation on the muzzle flow with dynamic mesh based on ALE equation[J]. Chinese Journal of Computational Mechanics, 2008, 25(4): 563-567. (in Chinese)
[8]王兵, 许厚谦. 后效期弹丸加速过程的数值模拟[J]. 弹道学报, 2008, 20(4): 84-87. Wang Bing, Xu Houqian. Numerical simulation of bullet accelerating process at after effect period[J]. Journal of Ballistics, 2008, 20(4): 84-87. (in Chinese)
[9]王兵, 许厚谦. 含有大位移动边界的复杂流场的数值模拟[J]. 计算物理, 2008, 25(4): 396-400. Wang Bing, Xu Houqian. Simulation of complex flows with large-scale moving boundaries[J]. Chinese Journal of Computational Physics, 2008, 25(4): 396-400. (in Chinese)
[10]代淑兰, 许厚谦, 孙磊. 含动边界的膛口流场数值模拟[J]. 弹道学报, 2007, 19(3): 93-96. Dai Shulan, Xu Houqian, Sun Lei. Numerical simulation of gun muzzle flow field including movable boundary[J]. Journal of Ballistics, 2007, 19(3): 93-96. (in Chinese)
Effect of the Artillery Recoil Movement on Muzzle Flow Field
LEI Hong-xia, WANG Zhi-jun
(School of Mechatronic Engineering, North University of China, Taiyuan 030051, China)
In view of the research status at home and abroad on muzzle flow field, the effects of the artillery recoil movement on muzzle flow field are studied based on computational fluid mechanics theory. Two numerical calculation models with and without recoil movement were built by using axisymmetric Euler equations and finite volume method (FVM). The unsteady state numerical simulation was carried out by using computational fluid dynamics software and dynamic grid technology. By comparing the numerical simulation results with and without recoil movement, the results show that the pressure ahead of muzzle is decreased and the pressure behind the muzzle is increased. Artillery recoil has little effect on the force of the gun chamber.
muzzle flow field; moving mesh; unsteady flow; artillery
1673-3193(2017)01-0036-06
2016-07-07
雷红霞(1978-), 女, 讲师, 博士生, 主要从事火炮发射动力学研究.
TJ301
A
10.3969/j.issn.1673-3193.2017.01.008
