基于择优连接和随机连接的协作通信网特性分析*

王 瑜， 李有文， 焦毅航， 刘丹伟

(1. 中北大学 理学院， 山西 太原 030051； 2. 内蒙古工业大学 理学院， 内蒙古 呼和浩特 010051)

基于择优连接和随机连接的协作通信网特性分析*

王 瑜1， 李有文1， 焦毅航1， 刘丹伟2

(1. 中北大学 理学院， 山西 太原 030051； 2. 内蒙古工业大学 理学院， 内蒙古 呼和浩特 010051)

协作通信高效的空间分集增益可以使通信性能得到提高， 但是由于协作通信网资源有限， 通信拥堵现象时有发生. 基于择优连接和随机连接对协作通信演化网络进行建模， 利用马氏链理论方法， 对协作通信网络的度分布稳定性的存在性进行严格证明， 得出网络度分布的精确方程， 发现通过调节概率p能够有效地控制和优化网络的传输容量. 通过数值模拟方法对网络度分布理论的结果进行分析验证. 所得分析结果可以为控制和预测协作通信演化网络提供参考.

复杂网络； 协作通信； 度分布； 马氏链

0 引 言

协作通信相对于直接通信可使目标用户实现快速、 高可靠性的数据传输， 可提供空间分集增益[1-3]， 合理分配和管理中继节点成为了协作通信中研究的重要问题．文献[4-5]提出了一种能使系统性能得到提高的算法， 即基于单个中继节点的最佳中继节点选取算法， 但其没有考虑多个中继节点协作通信所带来的系统性能提高．在一个通信系统中， 中继节点的数量选择并不是越多越好， 若选择数量较多的中继节点反而会使通信系统复杂度增加， 同时增加了成本， 因此如何选择合适数量的协同节点是一个重点研究的问题.合理地配置源节点和中继节点的发射功率， 可以提高协作通信的功率效率和最小化用户间的干扰. 文献[6-7]针对功率分配问题进行研究， 但是其只讨论了单中继节点的功率分配难题， 并没有对系统资源的优化配置进行讨论.

复杂网络理论通过点与链路可直观抽象地刻画出复杂网络系统， 并且对看似互不相同的复杂网络之间的共性进行分析研究， 从而找到处理有共性的复杂网络方法， 使我们更清楚地了解复杂系统的内在作用机理以及复杂网络系统构造及功能. Dorogovtsev等对BA无标度模型中各节点老化现象对网络系统的影响进行了研究[8]， Amaral等对老化、 容量以及成本等因素对网络的影响进行了综合分析研究， 并建立模型解释了真实的网络分布并不完全符合幂律分布[9]. 许多学者针对BA模型中的一些与真实网络不相符的问题， 提出了各类网络的动态演化模型[10-14]. 对复杂网络中优先连接机制也有许多学者进行了研究. 如文献[13] 中Kleibberge和Kumar利用拷贝机制代替了优先连接机制的方法形象地解释了网络呈现幂律现象的原因. Vázque等人提出了随机行走机制[15]. 针对BA模型只有加点操作的不足， 2000年Albert 和Barabási通过添加链路对网络的影响提出了扩展的BA模型. 针对BA模型中老节点总以大概率获得连接的情况与真实的复杂网络中不符的不足， Bianconi和Barabási提出了适应度模型， 该模型中以适应度来衡量决定连接. 但是， 研究发现现实的很多网络链接既存在优先连接特性又存在随机连接特性， 因此Liu等[16]提出了一种复杂网络模型， 该模型是基于优先连接和随机连接的混合模型.

文献[17]提出了一种网络协调博弈交易行为的演化模型， 但是由于择优连接会造成网络中老旧节点的度越来越大， 这样会使得网络中一部分通信容量有限的节点造成拥堵. 因此， 本文提出一种基于择优连接和随机连接的协作通信演化网络模型， 可起到控制和优化协作通信网资源的作用.

1 基于择优连接和随机连接的协作通信演化网络特性分析

1.1 模 型

基于复杂网络来研究协作通信网， 就要考虑其独特性. 由于协作通信网是实际应用网络的一种， 它的增长特性也遵循BA型网络， 但是每个节点都会受到其通信能力的限制， 所以只考虑BA型增长网络会使得一些节点通信拥堵. 因此， 本文考虑基于BA网络和随机网络混合的模型来研究协作通信网络， 这样会对BA网络的增长有所缓和.

优先连接和随机连接混合使用的概率模型为

其中， 0≤p≤1， 表示新节点在已存在网络中的节点随机连边的概率， 以概率1-p表示新节点在已存在网络中的节点选择度值较高的节点进行连边.k(i,t)表示在t时刻第i个节点的度为k.

初始条件： 网络中存在m0个节点， 节点的总度为N0. 假设每组协作通信至多存在一次时隙， 网络中的节点度至少为1(不存在孤立节点)， 在每个时间单位内完成以下4个步骤：

1) 在t时刻网络中增加一个度为m1的节点的概率为p1.

2) 在t时刻网络中增加一条链路的概率为p2.

3) 在t时刻网络中失去一个度为m2的节点的概率为p3.

4) 在t时刻网络中一条链路通信中断的概率为p4.

令p1+p2+p3+p4=1， 可以得到，t时刻网络中共m0+(p1-p3)t个节点， 总度数之和为N0+(2m1p1+2p2-2m2p3-2p4)t.

令ki(t)表示在i时刻加入网络的节点在t时刻的度数. 很容易得到， {ki(t)}(t=i,i+1,…)是非齐次马尔科夫链， 令P(k,i,t)=P{ki(t)=k}. 由模型的构造可知， {ki(t)}(t=i,i+1,…)的初始分布为P(k,i,t)=δk,m1， 其中δm1,m1=1； 当k≠m时，δk,m1=0， 那么就可以得出网络演化模型的转移概率方程为

(1)

1.2 度分布稳定性分析

定义 1 设p(k,i,t)表示i时刻进入系统的节点i在t时刻具有度数为k的概率， 则网络在t时刻的度分布定义为平均值

(2)

如果存在极限

(3)

则该网络具有稳定的度分布P(k,t),k=0,1,2,….

根据定义 1， 可得到如下引理：

证明 由协作通信演化网络构造可以得知， 节点i在刚加入网络的度为m1(P(m,i,i)=1)， 那么就有

(4)

式中： 1≤i≤t. 根据定义1， 可以得到

(5)

很容易可以看出方程(5)是一个差分方程， 求解可以得出

(6)

令

当t→∞时， 则有P(m1,t)=xt/yt. 由方程(6) 可以令差分方程为

(7)

(8)

由差分方程(7)和方程(8)， 可以得出

(9)

当t→∞时， 方程(9)可以近似变形为

(10)

上述引理表明， 协作通信网络演化过程中度为m1的节点在总节点中所占的比例P(m1)是参数p的函数.

当p=0时，

当p=1时，

对于在t时刻度为k(k>m1)的节点， 在t-1时刻的度可能为k(节点在t时刻不加边不删边)， 或k-1(节点在t时刻加边)， 或k+1(节点在t时刻删边). 因此， 根据引理1可以得到引理2.

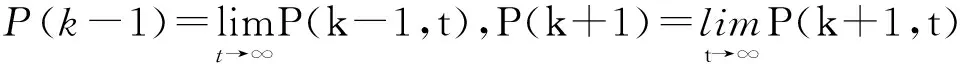
证明 证明过程类似引理1.

由引理2， 可以得出以下结论：

当p=0时，

当p=1时，

由引理1和引理2， 利用数学归纳法， 可以得出以下定理：

定理 1P(k) (k=m1,m1+1,…)存在， 且当k≥m1时， 那么就有

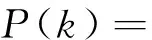
其中，

F2(p,m1)=[2m1p1+2p2-2m2p3-2p4-(2m1p1+2p2-2m2p3-2p4-p1+p3)p]×

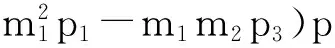
由上述定理1， 很容易得到：

当p=0时，P(k)≈k-1， 所得度分布为幂律分布； 当p=1时，

所得度分布为指数分布；

1.3 数值仿真

为了检验基于复杂网络的协同通信系统模型的分析结果， 对系统的度分布特性进行数值模拟. 假设初始状态系统由m0=4个节点全连通构成， 令m1=3， m2=3， p=0,0.5,1， p1=0.7， p2=0.13， p3=0.04， p4=0.13， N=500(见图1(a))， N=1 500(见图 1(b)).

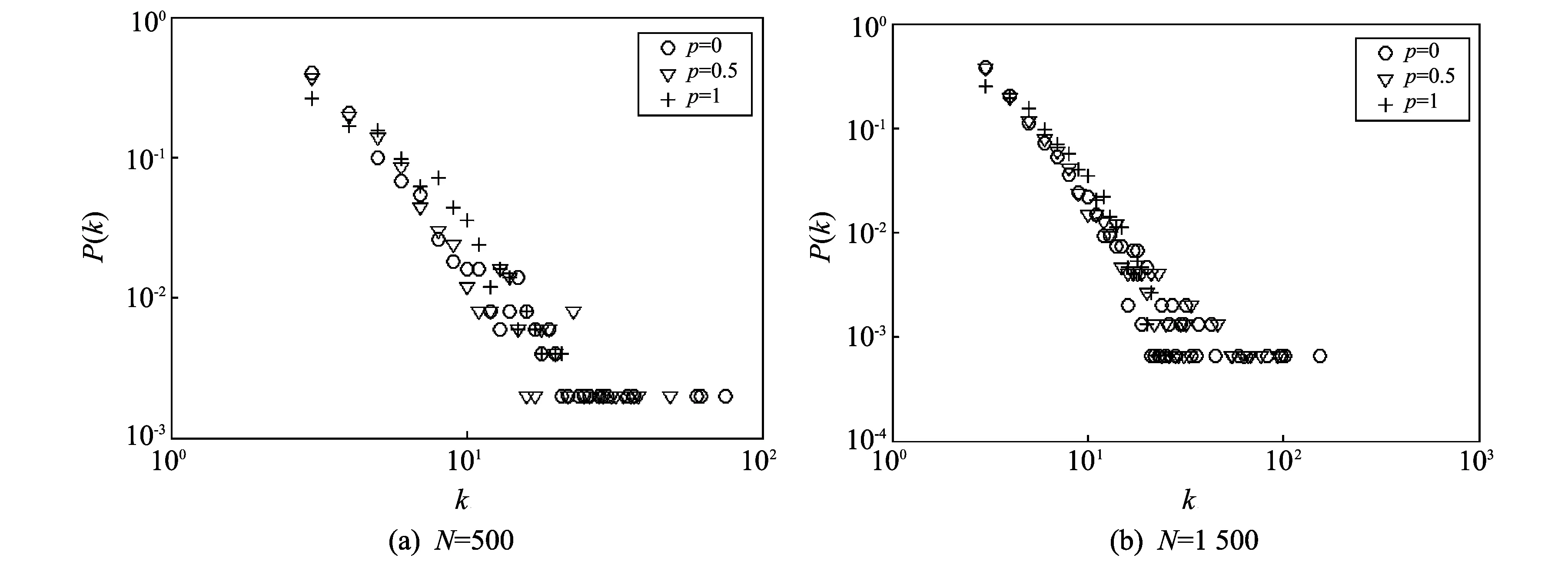
图 1 不同网络规模中不同值对网络度分布的影响Fig.1 Influence of degree distribution with different value of in different sizes of network

图 2 新增节点的不同度值对网络度分布的影响Fig.2 Influence of network degree distribution with different value of new node

由两图显然可以看出当系统中节点规模不断增大时， 系统中部分节点的最大度也在不断增大. 随着p值的增大， 网络的度分布由幂律分布逐渐退化为指数分布， 表明网络节点之间的连接逐渐趋于随机化. 当p=1时， 网络演化过程完全随机化.

令m1=4(图2(a))，m1=7(图2(b))，m2=3，p=0,0.5,1，p1=0.7，p2=0.13，p3=0.04，p4=0.13，N=500. 由两图显然可以看出， 当每个加入到系统中节点的度值逐渐增大时， 系统中节点的平均度也在不断增大. 当系统中节点规模不断增大时， 系统中部分节点的最大度也在不断增大. 随着p值的增大， 网络的度分布也由幂律分布逐渐退化为指数分布， 表明网络节点之间的连接逐渐趋于随机化. 当p=1时， 网络演化过程也完全随机化. 当网络中某些节点由于资源有限时， 为了防止通信拥堵现象发生， 可以通过调节p值来优化网络传输性能.

2 结 语

本文根据协作通信网络的实际特征， 提出网络演化过程的4个步骤， 并利用马氏链理论方法对网络演化过程进行建模和分析.结果表明： 当p=0时， 所得度分布为幂律分布； 当p=1时， 所得度分布为指数分布； 当0

本文虽然通过混合机制的连接方法对协作通信演化网络进行了建模， 但是这仅适应于协同通信网络中老旧节点的通信能力有所保障的情况下. 如果协同通信网络中新增节点由于其具有良好的性能和更高的通信容量时， 则需要通过建立适应度形式的网络演化模型进行分析， 这将是后续需要研究的问题.

[1]Foschini G J, Gans M J. On the limits of wireless communications in a fading environment when using multiple antennas[J]. Wireless Personal Communications, 1998, 6(3)： 311-335.

[2]Telatar I E. Capacity of multi-antenna Gaussian channels[J]European Transaction of Telecommunications, 1999, 10： 555-595.

[3]Foschini G J. Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas[J]. Bell Labs Technical Journal, 1996, 1(2)： 4l-59.

[4]Trana V C, Leb M T, Trana X N. MIMO cooperative communication network design with relayselection and CSI feedback[J]. Int. J. Electron. Commun. (AEÜ) , 2015, 69： 1018-1024.

[5]Jing Tao, Zhang Fan, Cheng Wei, et al. Online auction-based relay selection for cooperative communication in CR networks[J]. EURASIP Journal on Wireless Communications and Networking, 2015, 20： 1-12.

[6]Zhai Wenyan, Sun Yanjing, Xu Zhao, et al. Power allocation and mode selection methods for cooperative communication in the rectangular tunnel[J]. International Journal of Mining Science and Technology, 2015, 25： 253-260.

[7]Atefe M L, Ali S. Power allocation in cooperative communication system based on stackelberg game[J]. Wireless Pers Commun , 2015, 84： 123-135.

[8]Dorogovtsev S N, Mendes J F F, Samukhin A N. Structure of growing networks with preferential linking[J]. Physical Review Letters, 2000, 85(21)： 4633-4636.

[9]Amaral L, Scala A, Barthélémy M, et al. Classes of small-world networks[J]. Proceedings of the National Academy of Sciences, 2000, 97(21)： 11149-11152.

[10]Holme P, Kim B J. Growing scale-free networks with tunable clustering[J]. Physical review E, 2002, 65(2)： 026-107.

[11]Dorogovtsev S N, Mendes J F F, Samukhin A N. Growing network with heritable connectivity of nodes[J]. Physics, 2000, 9： 1-5.

[12]Bianconi G, Barabási A L. Bose-Einstein condensation in complex networks[J]. Physical Review Letters, 2001, 86(24)： 5632-5635.

[13]Kleinberg J, Kumar R, Raghavan P, et al. The web as a graph： Measurements, models, and methods[J]. Computing and Combinatorics, 1999： 1-17.

[14]Barabási A L, Dezso Z, Ravasz E, et al. Scale-free and hierarchical structures in complex networks[C]. AIP Conference Proceedings, 2003, 661： 1.

[15]Vázquez A, Moreno Y. Resilience to damage of graphs with degree correlations[J]. Physical Review E, 2003, 67(1)： 015-101.

[16]Liu Z H, el al. Connective distribution and attack tolerance of general networks with both preferential and random attachments[J]. Phy. Lett. A, 2002, 303： 337-344.

[17]Bian Yuetang, Xu Lu, Li Jinsheng. Evolving dynamics of trading behavior based on coordination game in complex networks[J]. Physica A , 2016, 449： 281-290.

Performance Analysis of Cooperative Communication Networks Based on Preferential and Random Attachments

WANG Yu1， LI You-wen1， JIAO Yi-hang1， LIU Dan-wei2

(1. School of Science, North University of China, Taiyuan 030051, China；2. School of Science, Inner Mongolia University of Technology, Hohhot 010051, China)

Although cooperative communication has the characteristics of high efficiency of spatial diversity gain, communication congestion is occurred by the limited resources of cooperative communication network. By the method of Markov chain theory, the cooperative communication network evolution model was presented based on preferential and random attachment, and the existence of distribution stability was strictly proved and given the exact equations for the degree distribution of the network. It is found that the transmission capacity of the network can be effectively controlled and optimized by adjusting the probability ofp. Numerical simulation was carried out to verify the theoretical results of the network degree distribution. The analysis results provide reference for the control and prediction of the evolution of cooperative communication networks.

complex network; cooperative communication; degree distribution; Markov chain

1673-3193(2017)01-0060-06

2016-06-12

国家自然科学基金资助项目(11301491)

王 瑜(1990-)， 男， 硕士， 主要从事应用数学研究.

李有文(1967-)， 男， 副教授， 主要从事生物数学、 层次分析法等研究.

TN911.1； O157.6

A

10.3969/j.issn.1673-3193.2017.01.012