非接触检测中螺纹图像牙型边界修正研究

孙珂琪

(陕西铁路工程职业技术学院，陕西 渭南 714000)

非接触检测中螺纹图像牙型边界修正研究

孙珂琪

(陕西铁路工程职业技术学院，陕西 渭南 714000)

利用图像的非接触检测螺纹是一种高效的检测方法；检测中，精准的获取到螺纹图像的牙型边界是检测的关键，而现有的图像处理技术并不能消除由于螺纹旋线对螺纹图像的影响；针对螺纹图像中牙型边界被遮挡的问题，从圆锥螺纹的几何空间关系分析图像产生误差的原因，建立圆锥螺纹数学模型，得到误差的方程；最后再设计了图像检测系统，根据误差方程修正螺纹图像、提取参数，经验证，此方法可以提高螺纹的检测精度，且通用在圆锥螺纹与圆柱螺纹中。

图像处理；螺纹检测；牙型边界；修正

0 引言

螺纹是一种应用非常广泛的零件，在工程、工业、电子等行业中都是不可取代的，它主要用在零件之间连接、固定和密封等[1]。在设备的使用中，螺纹关乎着设备的正常运行、产品的质量，甚至关系到人身安危[2]。螺纹的大批量的需求与生产，对检测的精度与效率有很高的要求。

早期人们利用检测工具(如量规、卡尺等)检测螺纹，需要检测人员操作检测工具逐个检测、记录与比较，检测速度慢、效率低、容易出现人为误差，而且在检测时测量工具容易损伤螺纹表层，影响检测结果[3]。为了提高检测精度，浙江大学的徐爱群[4]等人基于激光三角测量原理，研制了非接触自动螺纹检测仪，用激光测量头检测螺纹轮廓，将检测精度提高到1.5 μm。天津大学的张红岩[5]等人提出了大型螺纹自动检测系统，利用新型螺纹探头实现接触式测量，高检测精度提高到1.0 μm。这种方法避免了检测工具与被测螺纹的接触，但是检测精度仍然不高。随着科技发展，硬件设施不断提高，图像处理软件与图像处理技术也愈发成熟[6-7]。将图像处理应用在零件检测中被很多人接受与研究[8-11]。随之，chengchuangliu[12]提出用线性回归和图像分析测量螺距。天津大学的左建中[13]等人提出了技术视觉在螺纹检测中的应用，检测了螺纹的中经、螺距、牙型角3个重要参数。何富军[14]等通过改进CCD相机的光轴角度，消除图像获取中的误差。但这种方法仍然不能得到精确的螺纹图像。沈萌红[15]等人提出对圆柱螺纹牙型失真的矫正，通过模型的建立，可以通过计算与拟合得到圆柱螺纹的精确图像，但是仅能用在圆柱螺纹中。

1 螺纹成像分析

拍摄到高精度螺纹图像是检测螺纹的基础，而图像的拍摄会受到各种因素的影响，螺纹放置的角度、摄像机拍摄角度、螺纹自身的几何形状、螺纹表面的杂质、光线、噪声等，都会使图像产生不同误差与畸变。由光线、噪声对螺纹造成的影响，图像处理方法可以基本修正，对现有的检测设备改良之后也可消除螺纹表面杂质的影响。但是拍摄角度、螺纹形状对螺纹图像的影响却是难以消除。

1.1 图像获取角度螺纹成像的影响

在现有的检测方法中，螺纹检测装置大致可分为两类，如图1所示，一种是通过调整被测螺纹的角度，使摄像机轴线平行于被测螺纹旋线。另一种被测螺纹中心轴线与摄像机轴线垂直。

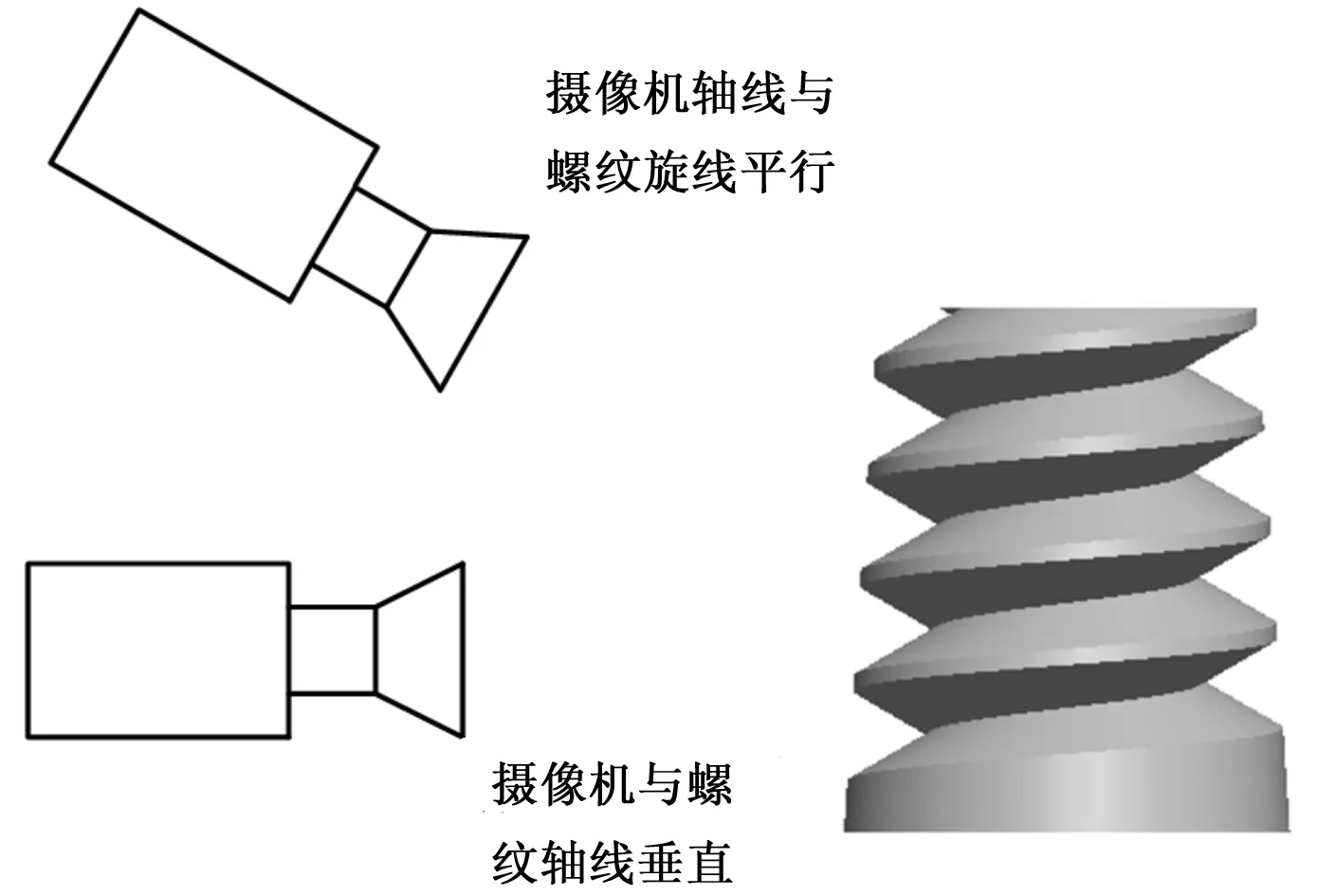
图1 螺纹拍摄角度

被测螺纹与摄像机轴线垂直的情况下，对于每一种螺纹，都会因为螺纹旋线的旋转角度影响真实的螺纹牙型轮廓。调整螺纹角度之后，该方法考虑到了螺纹旋线的旋转角度对螺纹真实图像的影响，它对于消除圆柱螺纹图像的误差产生是非常有用，但是却不能消除圆锥螺纹中由于螺纹端面的不断变化而对螺纹图像产生的影响。而且对于不同型号的被测螺纹，螺纹与摄像机之间的角度都需要调整，增大了检测的复杂度。

不论哪种方法获取到的螺纹图像，经过现有图像处理，仍然不能得到实际的螺纹牙型边界。文中主要针对被测螺纹中心轴线与摄像机轴线垂直的情况下，以圆锥螺纹为研究对象，建立数学模型，消除由螺纹几何关系对螺纹牙型轮廓的影响。圆柱螺纹的几何参数比圆锥螺纹简单，改变圆锥螺纹模型中的一些参数，就可以适用在圆柱螺纹中。

1.2 螺纹形成的几何关系对成像的影响

取一个标准圆锥螺纹，在其中心建立坐标系，如图2所示，设有一条牙型线MN，与圆锥螺纹基面交于点M，MN绕螺纹旋线旋转180°之后为另一条牙型线M1N1，理论上M1N1为螺纹牙型边界，但其实拍摄到的螺纹图像中，真正的牙型轮廓M1N1是被遮挡的。如图2所示。

图2中M2N2即为由于拍摄角度、螺纹锥度、螺旋线而影响得到的螺纹图像边界，设牙型线MN上有一点A，MA之间的距离为t，如图3所示，即在M1N1上就对应有点A1，设点A1是真实的螺纹牙型边界上的一个点，但是它并不在图像中的牙型边界，它被牙型线MN旋转到某一角度φ时，M2N2上的一点B2遮挡了，则对应在MN上就有一点B，设AB之间的距离为t1。

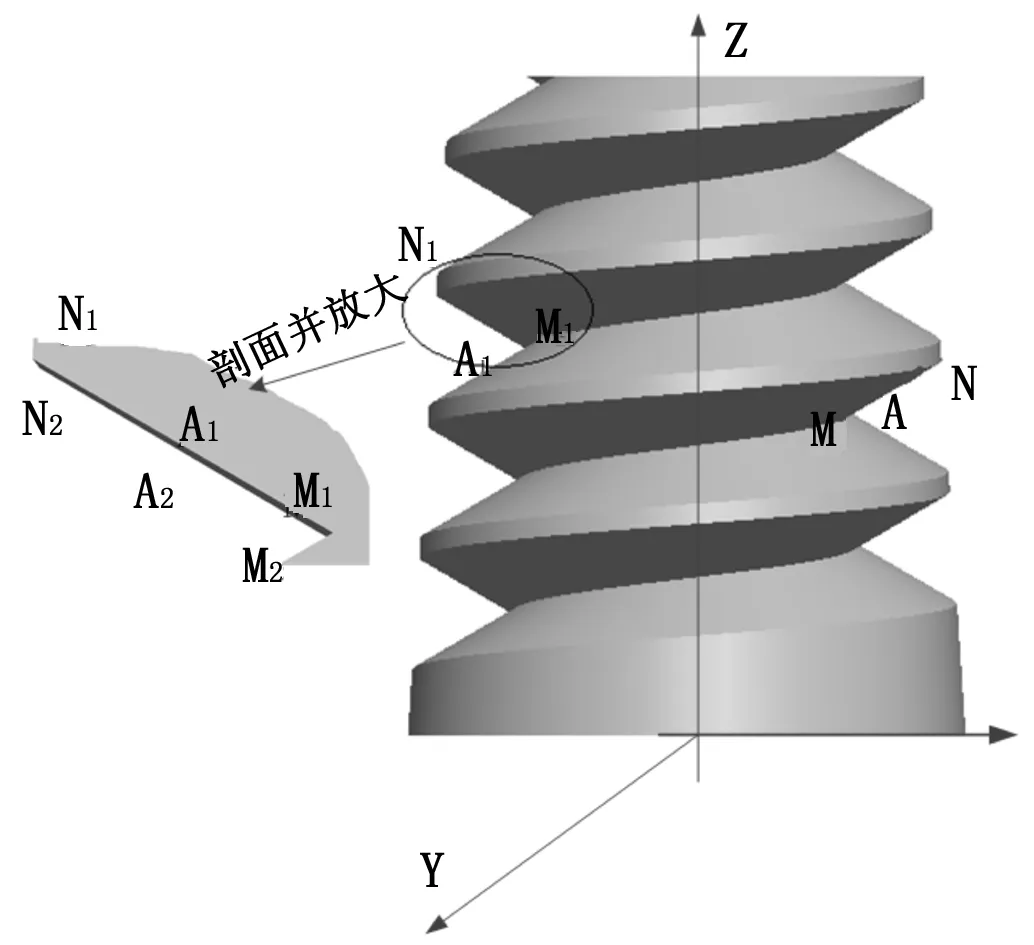
图2 螺纹成像分析

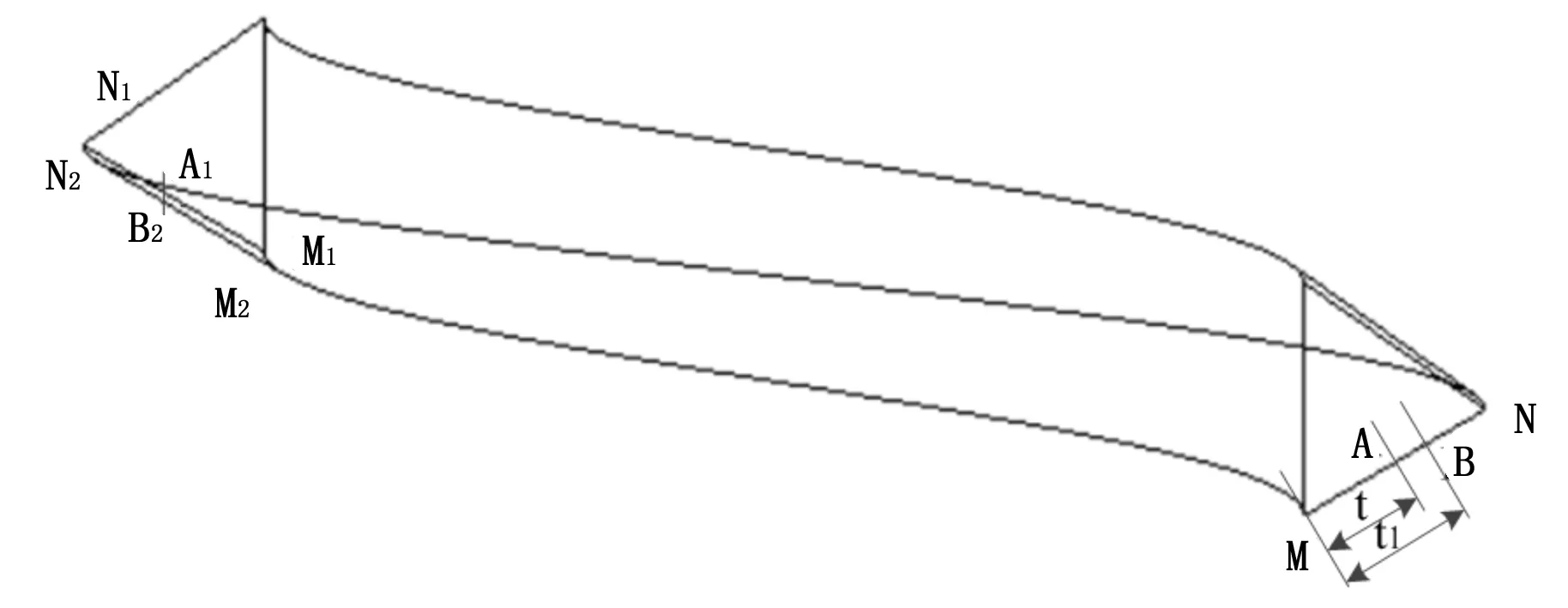
图3 螺纹几何关系

2 螺纹数学模型建立

设点M的坐标为：

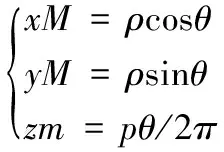
(1)

式中,θ为点A绕圆锥基面运动过的角度，即圆锥螺旋角；p为圆锥螺纹螺距。

根据圆锥螺纹几何关系，可以计算出：

(2)

式中,γ为圆锥螺纹的锥度半角；r为点M所在的圆锥端面半径。即点M坐标可为：

(3)

设牙型线MN与螺纹基面夹角为β，根据螺纹几何关系可知，β为牙型角一半，即牙型半角，可列出MN的方程(4)。

普通的牙型并不是标准的三角形，为了便于计算，我们将牙型角看作标准的三角形，可以得出，式中t的取值范围。

(4)

式中,

(5)

为了便于计算，假设牙型线MN为θ=0时的牙型线，真实的牙型线M1N1即为θ=π时的牙型线，螺纹图像中得到牙型边界M2N2即为θ=φ(π/2≤φ≤π)时的牙型线。

当θ=π时，M1N1的方程为：

(6)

当θ=φ时，M2N2的方程为：

(7)

要修正螺纹图像，即要得到螺纹的图像中牙型边界，实际的螺纹牙型边界，再得到它们之间的差值方程，便可以对螺纹图像进行重构与修正。即用M1N1的方程减去M2N2的方程：

(8)

(9)

这时，我们只需得到旋转角度φ与螺纹牙型线上的点之间的关系，就可以根据牙型上的点来修正螺纹图像了。

根据式即可得到点B2的坐标如式(9)。

从图可以看出，点B2和点A1在X轴方向上的距离是相等的，最终得到：

(10)

化简可得t与t1的关系如下：

(11)

将t1代入zB2中，要的到图像中遮挡到点A1的牙型边界点的点B2，即求出当φ为多大时，zB2有极小值：

(12)

求导并化简可得：

(13)

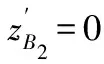
(14)

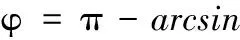
(15)

将上式代入zB2的方程中，即可得到圆锥螺纹的图像轮廓方程，用理论的轮廓方程减去图像轮廓方程，就可以得到差值方程。

(16)

式中,t为牙型上任一点到牙根部的距离，它的取值范围与螺纹的规格有关。r为螺纹的端面半径，对于不同的螺纹，它的值是不断变化。p为螺纹螺距；γ为螺纹锥度半角；β为螺纹的牙型半角。

3 圆柱螺纹差值方程

当圆锥螺纹的锥度半角为0时，圆锥螺纹即为圆柱螺纹，此时，圆锥螺纹的差值方程即为圆柱螺纹的差值方程：

(17)

4 实验验证

4.1 实验装置

为了验证该数学模型的正确性，设计了一套螺纹检测系统，改进了螺纹放置装置，它是一个可以旋转的圆盘状，就可以实现螺纹的不间断供给。[16]在检测之前，螺纹固定装置下方设计了可以喷气除杂的设备，实现检测前无接触的螺纹表面杂质的处理。软件系统选用Matlab数学分析和Labview图像处理模块来实现。检测过程如图4所示。

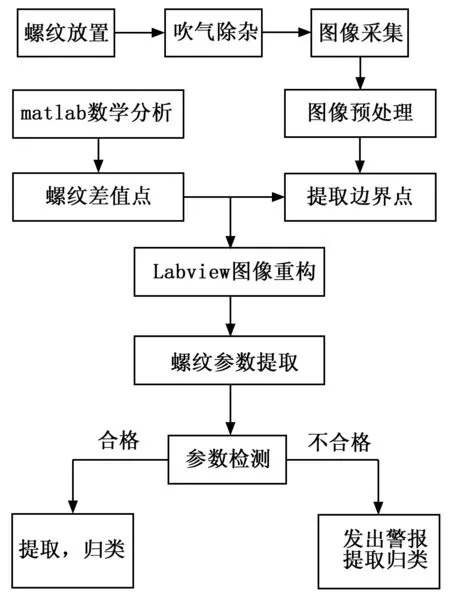
图4 检测流程图

4.2 数学分析与图像重构

取型号为NPT1/2的60°标准密封管锥螺纹，采集到螺纹图像之后，运用Labview中得到visio assisant模块对图像畸变矫正、二值化处理、边缘检测、目标分割之后的图像为图5所示。

图5 图像预处理

取单独一个牙型角出来，在其中一条牙型线上取十个点，如图6，通过图像标定得到图像中每个点的参数，再通过Matlab数学分析得到理论牙型点、差值牙型点，最终得到修正后的牙型点，如图7～图8,最终得到的参数对比如表1。

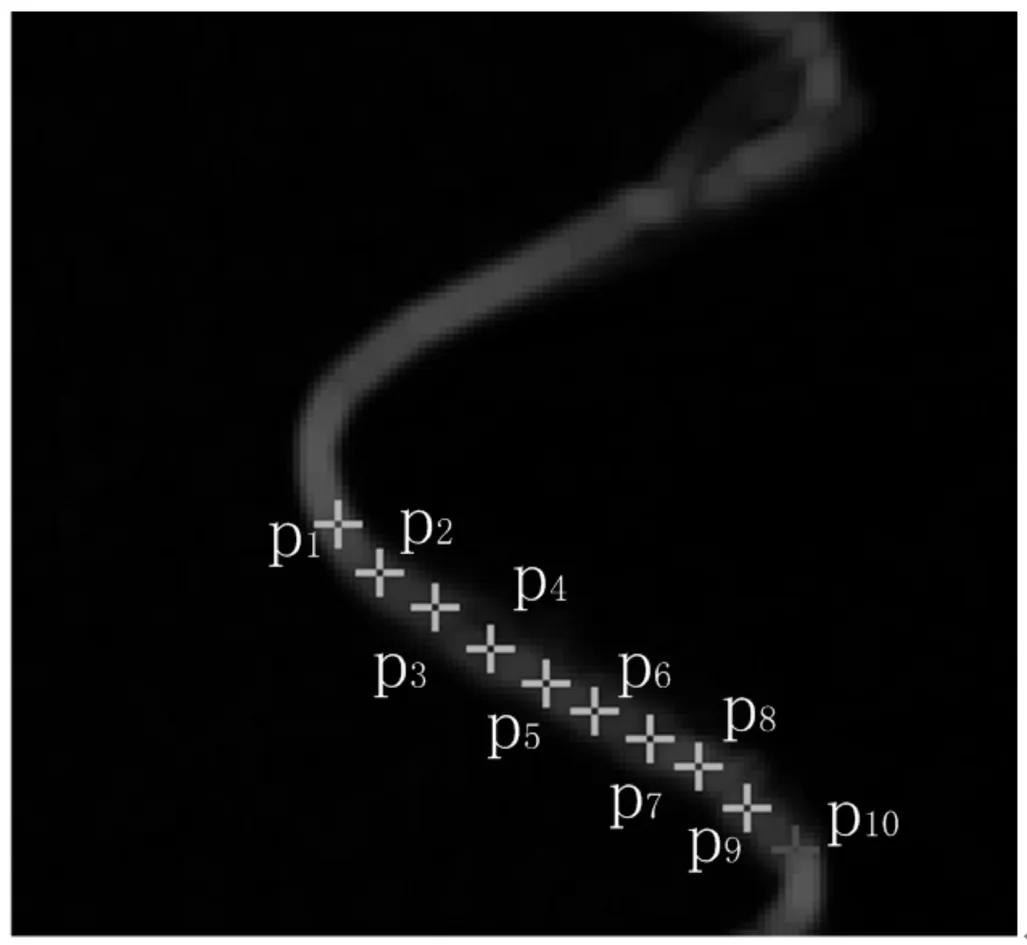
图6 牙型参数提取

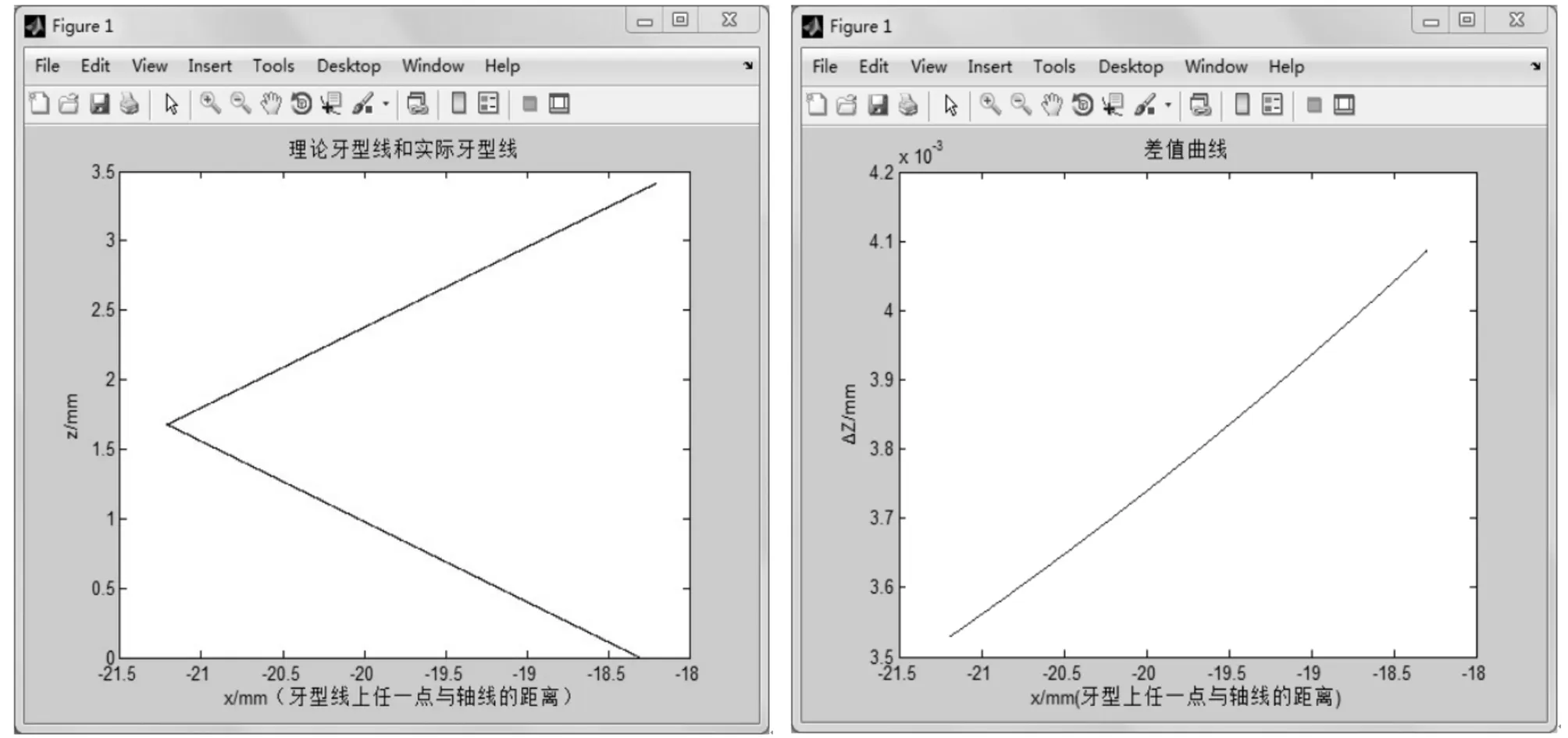
图7 牙型角仿真 图8 差值曲线

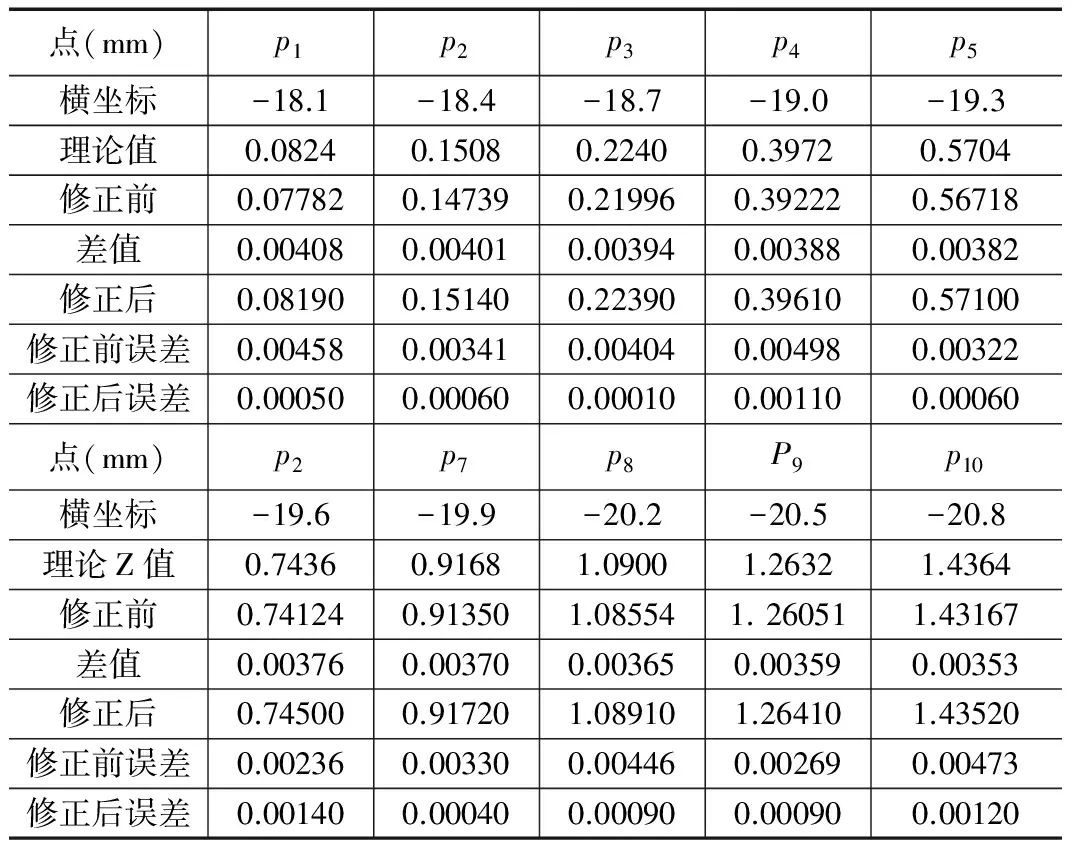
点(mm)p1p2p3p4p5横坐标-18．1-18．4-18．7-19．0-19．3理论值0．08240．15080．22400．39720．5704修正前0．077820．147390．219960．392220．56718差值0．004080．004010．003940．003880．00382修正后0．081900．151400．223900．396100．57100修正前误差0．004580．003410．004040．004980．00322修正后误差0．000500．000600．000100．001100．00060点(mm)p2p7p8P9p10横坐标-19．6-19．9-20．2-20．5-20．8理论Z值0．74360．91681．09001．26321．4364修正前0．741240．913501．085541．260511．43167差值0．003760．003700．003650．003590．00353修正后0．745000．917201．089101．264101．43520修正前误差0．002360．003300．004460．002690．00473修正后误差0．001400．000400．000900．000900．00120

从表1中可以看出，修正后的图像中牙型点，和理论牙型点之间的误差比修正前小很多，通过相同的方法，对整个螺纹牙型边界修正，图9为修正后的牙型轮廓。

图9 修正后图像

4.3 参数提取与检测

根据修正之后的螺纹图像，获得螺纹的的最终轮廓边界，检测提取所需参数，得到螺纹的中经、螺距、牙型角的参数如表2。

表2 检测结果对比

从表2中可以看到，经过螺纹边界修正之后，中经和螺距的误差都在0.4以内，牙型角误差在0.013，比修正前减小了很多。值为了验证检测的有效，再取10个螺纹，每个螺纹进行10次检测，最终中经误差在0.5以内，螺距误差在0.5以内，牙型角的误差在0.015以内。

5 结论

(1)文中从拍摄角度、外界干扰、螺纹几何关系等方面分析非接触图像检测螺纹中获取的图像产生误差的原因，通过数学建模与分析，得到了通用的修正螺纹的方程，解决了图像畸变的问题。

(2)改进螺纹检测装置，运用matlab的数学分析与模型仿真与Labview的图像处理技术相结合，可以实现螺纹不间断的高精度检测。

[1] 卜 晨.基于机器视觉的外螺纹检测方法以及实验研究 [D].广州：华南理工大学,2011.

[2] 邓细凤.基于图像处理的螺纹表面缺陷技术研究 [D].重庆：重庆大学,2012.

[3] 刘兴荣,张小希,马桂茹,等.圆锥螺纹塞规测量方法综述[J].计测技术, 2008.28 (6):5-8.

[4] 徐爱群,项占琴,陈子辰.非接触自动螺纹检测仪的研制[J].浙江大学学报,2005.39(8):1179-1183.

[5] 张红岩,张国雄,大螺纹在线测试系统[J].机械工程学报,2008,44(12): 199-202.

[6] 林慧英，苏 建，等.基于图像畸变矫正的摄像机标定方法[J].吉林大学学报(工学版),2007(3),37(2). 433-437.

[7] Tsai R Y. A versatile camera calibration technique for high accuracy 3D machine vision metrology using off the shelf TV cameras and lenses[J]. IEEE Journal of Robotics and Automation, August 1987, 3(4): 323-344.

[8] Pavlidis T, Liow Y T. Integrating Region Growing and Edge Detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence(TPAMI), 1990, 12(3): 225-233.

[9] Yu L J, et al. Application of Digital Image Analysis Method in Metric Screw Thread Metrology[J]. Journal of Shanghai University (English Edition), 2004,8(2): 208-212.

[10] Jiang X Y, Horst Bunke. Edge Detection in Range Images Based on Scan Line Approximation[J]. Computer Vision and Image Understanding, 1999, 73(2):183-199.

[11] 陈曼龙，基于机器视觉的锥螺纹参数测量方法[J].计算机测量与控制,2012,20(5)1166-1168.

[12] Liu Chenchung, Chen Wenyuan. Screw pitch precision measurement using simple linear regression and image analysis[J] Applied Mathematics and Computation 178 (2006) 390-404.

[13] 左建中,刘 峰，张定绍.机器视觉技术在螺纹检测中的应用[J].机械设计与制造,2006,4(4):113-114.

[14] 何富君，张瑞杰,兰 爽,等.圆锥外螺纹的线阵CCD非接触检测方法[J].哈尔滨工业大学学报,2008,40(7): 1169-1180.

[15] 沈萌红,沈绍锋,王贤成,等.非接触检测圆柱螺纹牙型失真校正[J]农业机械学报,2011,42(10)：224-229.

[16] 孙珂琪,郑 堤,陈俊华图像检测螺纹的系统设计[J]计算机测量与控制,2015,23(3):893-896.

Study on Revision of Thread Tooth Form Based on Non-Contact Measurement

Sun Keqi

(Shanxi Railway Insitute, Weinan 714000,China)

Non-contact detection based on image is an efficient detection method, during the detected, to obtain the image of the tooth profile of the taper thread accurately is the key of the detection. The existing image processing technique can not eliminating the influences of helix line to the thread image. Based on the problem of the tooth profile are shaded, analyzed the reason of the errors from the geometry relation of the thread, then get the differential equation. At last, established a system for detecting the thread, according to the differential equation, revised the taper thread tooth, extracting parameters. After the validations, the new method can improve the precise of measurement based on image, be used in both taper thread and parallel screw thread

image processing; detecting thread; tooth profile; revised

2016-07-14；

2016-08-17。

孙珂琪(1990-)，女，陕西渭南人，助教，主要从事机器视觉、图像处理方向的研究。

1671-4598(2017)01-0192-04

10.16526/j.cnki.11-4762/tp.2017.01.054

TG85;TH471

A