砾质土心墙料蠕变对坝体应力变形的影响

徐 晗，程展林，左永振，潘家军

（长江科学院 水利部岩土力学与工程重点实验室，湖北 武汉 430010）

1 研究背景

随着西部大开发战略的进行，土石坝的建设规模越来越大，坝高逐步向300 m级发展，国内学者开始重视高土石坝的蠕变对坝体应力变形的影响［1-3］。目前，国内外针对堆石料等排水性能较好材料的蠕变特性的研究较多［4-10］，提出了较多的针对粗粒土的蠕变模型。而对砾质土蠕变特性的研究甚少［11］，原因在于砾质土含有大量渗透性较低的细粒，大试样固结排水效果差，排水不充分会导致瞬间变形偏小，试验中蠕变变形不真实。

长江科学院提出在砾质土心墙料大型三轴试验中采用钻孔灌砂以加速试样的排水固结［12］，取得了较好的试验效果。在此基础上进行了某砾质土心墙料的蠕变试验，获得了砾质土心墙料的蠕变模型及参数，编制了相应的蠕变子程序，建立了高心墙坝的三维有限元模型，采用非线性有限元研究了砾质土心墙料蠕变对坝体应力变形的影响。

2 砾质土心墙料的蠕变试验

砾质土心墙料控制干密度为2.20 g/cm3，试验级配是以砾质土心墙料平均级配经缩尺后的级配，如下表1所示，三轴试样为Φ300×600 mm，试验中对试样进行试样内部成孔并灌注标准砂，以加速试样的排水固结。5个钻孔直径均为6 mm，砂芯的面积置换率占0.2%，三轴试验表明，砂芯的设置对土试样的强度及变形特性基本无影响［12］。

表1 砾质土心墙料试验级配

根据高坝的坝高等实际设计资料，设置0.8 MPa、1.6 MPa、2.4 MPa三种围压，对每一种围压，分别施加0.2、0.4、0.6、0.8四种偏应力水平，研究在不同偏应力水平及不同围压条件下，砾石土心墙料的蠕变特性。各级应力水平下的竖向荷载是根据常规三轴试验确定的强度指标及相应的围压计算，变形稳定以每24 h的轴向变形量不大于0.02 mm为控制标准，当变形趋于稳定后施加下一级荷载。

其应力水平0.2、0.4、0.6和0.8时轴向应变和体积应变与时间的关系曲线见图1—4所示，可知砾石土心墙料的蠕变过程是逐渐趋于停止的衰减曲线，前期的瞬时变形较大，后期逐渐趋于稳定。

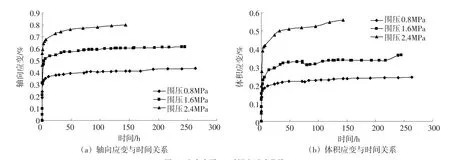
图1 应力水平0.2时蠕变试验曲线

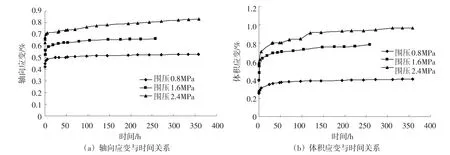
图2 应力水平0.4时蠕变试验曲线

图3 应力水平0.6时蠕变试验曲线

3 粗粒土的九参数幂级数蠕变模型

九参数幂级数蠕变模型由长江科学院提出，根据试验结果认为粗粒土的轴向蠕变和体积蠕变均可用幂函数表达［7］：

图4 应力水平0.8时蠕变试验曲线

式中：εaf和εvf分别为某个应力状态下最终轴向蠕变量和最终体积蠕变量，εa()t和εv()

t分别为0～t时段内累计的轴向和体积蠕变量， λa和λv分别为累计轴向和体积蠕变相关的时间幂指数。

最终轴向蠕变量εaf与围压σ3应及力水平SL有如下关系：

式中：c和d为无量纲参数。

λa与应力水平SL基本无关，且λa与围压σ3的关系可以用如下幂函数表示：

式中：η和m为无量纲参数。

εvf与围压σ3和应力水平SL可用线性函数拟合：

表2 坝料九参数幂函数蠕变本构模型参数

式中：cα、dα、cβ和dβ为无量纲参数。

λv与应力状态关系不明显，可以假定为常数：

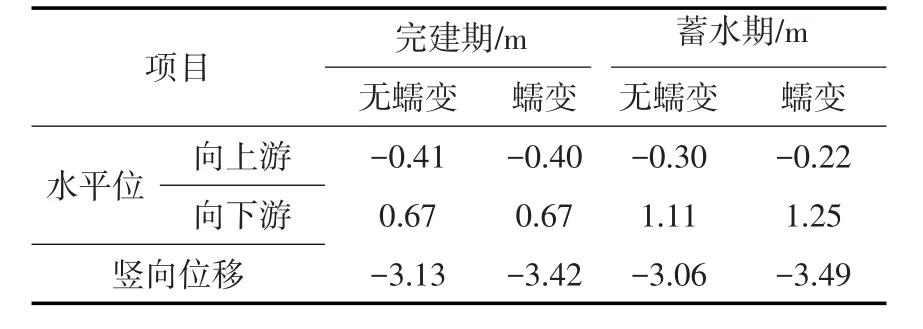
表3 考虑蠕变与不考虑蠕变结果比较

开展了上、下游堆石料、砾质土心墙料的室内蠕变试验，对试验数据进行分析后表明，长江科学院粗粒土九参数幂级数蠕变模型能较好地描述砾质土心墙料的蠕变特性。各坝料试验所获所得的九参数幂函数蠕变本构模型参数见下表2所示，在公式中时间单位以小时计，应力单位以MPa计。值得说明的是，堆石料的缩尺方法有一定的尺寸效应，会影响堆石料的蠕变变形，总体上说，大尺寸试样的变形量大于小尺寸试样的变形量，因而会导致数值计算沉降值会小于实际工程实测值［6］。

图5 心墙不同高程监控点位置示意

图6 监控点位移蠕变过程

4 蠕变对坝体变形的影响

建立某高土质心墙堆石坝三维有限元模型，将分析结果分别按照完建期与蓄水期整理。采用三维有限元软件Marc计算，得到的考虑蠕变与不考虑蠕变的坝体极值结果比较见表3所示。

图7 不考虑蠕变蓄水期心墙最大断面主应力等值线/MPa

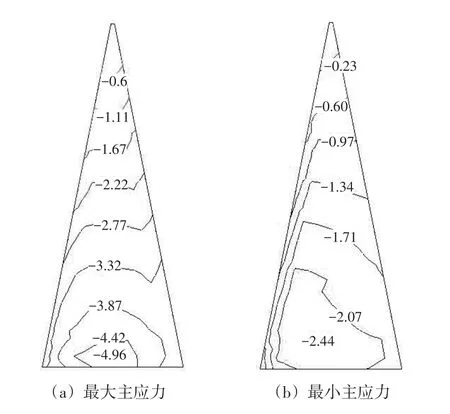
图8 考虑蠕变蓄水期心墙最大断面主应力等值线/MPa

以图5中最大断面心墙内部4个不同高程的节点为例，图6监控点位移蠕变过程曲线表示心墙内部4个不同高程位置的节点的水平位移、沉降蠕变过程。心墙底部监控节点1经历的蠕变时间最长，在逐步的加载过程中产生了明显的蠕变，并且蠕变逐渐趋于稳定；心墙顶部监控节点4经历的蠕变时间最短，但也逐步趋向于稳定值。对比四个不同位置高程的监控节点水平位移与沉降蠕变曲线可知，其计算得到的蠕变曲线与试验曲线规律基本一致。

当考虑坝体蠕变后，蓄水期坝体最大沉降为3.49 m，比不考虑蠕变的坝体的最大沉降增大约43 cm左右；考虑蠕变效应蓄水期坝体最大顺河向位移为1.23 m，比不考虑蠕变的坝体最大顺河向位移增大约12 cm，表明蠕变效应主要引起坝体下沉，对水平位移的影响较小。

表4 考虑心墙蠕变与不考虑心墙蠕变结果比较

5 蠕变对坝体应力的影响

应力符号以受压为负。图7—8分别为不考虑蠕变与考虑蠕变蓄水期心墙最大断面主应力等值线图，可知两者规律基本接近，只是数值有差异。考虑蠕变后，心墙的最大主应力极值由-5.02 MPa下降到-4.96 MPa，心墙的最小主应力极值由-2.51 MPa下降到-2.44 MPa，究其原因在于心墙较软，其蠕变的速率要明显快于周围堆石体，进一步加剧了心墙的拱效应，不利于心墙的受力，因此，应采取措施减小心墙的蠕变率。

为了研究心墙料蠕变与否对坝体应力变形的影响，分别计算对比了考虑所有坝料的蠕变特性与仅考虑上、下游堆石体的蠕变两种工况，其计算结果如下表4所示。

由表4可知，如果不考虑心墙料的蠕变而仅考虑堆石体的蠕变，蓄水期坝体变形最大值为-3.22 m，与完全不考虑蠕变最大沉降-3.06 m相比，仅增加了16 cm的蠕变量，而考虑了心墙料蠕变后增加了43 cm的蠕变量，说明上、下游坝壳的蠕变对心墙自身变形的影响较小，蠕变计算中应该考虑砾质土心墙料蠕变的影响。

6 结论

（1）上、下游坝壳的蠕变对心墙自身变形的影响较小，需要在坝体应力变形计算中考虑心墙料蠕变的影响，因而有必要进行砾质土心墙料的蠕变试验，试验结果表明九参数幂级数蠕变模型能较好地描述砾质土的蠕变特性；（2）蠕变效应主要引起坝体下沉，对坝体水平位移的影响不大，考虑了坝体的蠕变后，坝体的变形会更真实地反映实际坝体的运行状况；（3）如果砾质土心墙料的蠕变速率快于周围堆石体，则心墙的大、小主应力与不考虑蠕变相比有所减小，蠕变效应会进一步增加心墙拱效应，对心墙水力劈裂不利；反之，蠕变效应会减小心墙拱效应，有利于抑制心墙水力劈裂。

［1］程展林，潘家军 .水布垭面板堆石坝应力变形监测资料分析［J］.岩土工程学报，2012，34（12）：2299-2306.

［2］ATHANASIU C，SIMONSEN A S，SOEREIDE O K，et al.Elastic and creep settlements of rock fills［C］//Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering.2005，Vols 1-5：1837-1843.

［3］ZIMMERER M M，SCHANZ T，LINS Y，et al.Numerical analysis of water reservoir dam-Prediction of long term performance of Versetal dam［C］//Proceedings of the International Symposium on Dams and Reservoirs under Changing Challenges-79 Annual Meeting of ICOLD.2011：321-330.

［4］李海芳，张茵琪，金伟，等 .堆石料蠕变特性试验研究［J］.水力发电学报，2013，32（1）：213-217.

［5］梁军，刘汉龙 .面板坝堆石料的蠕变试验研究［J］.岩土工程学报，2002，24（2）：257-259.

［6］花俊杰，周伟，常晓林，等 .堆石体应力变形的尺寸效应研究［J］.岩石力学与工程学报，2010，29（2）：328-335.

［7］程展林，丁红顺 .堆石料蠕变特性试验研究［J］.岩土工程学报，2004，26（4）：473-476.

［8］朱晟，王永明，徐骞 .粗粒筑坝材料的增量蠕变模型研究［J］.岩土力学，2011，32（1）：3201-3207.

［9］王勇，殷宗泽 .一个用于面板坝蠕变分析的堆石蠕变模型［J］.岩土力学，2000，21（3）：227-230.

［10］李国英，赵魁芝，米占宽 .堆石体蠕变对混凝土面板坝应力变形特性的影响［J］.岩土力学，2005，26（S）：117-120.

［11］王观琪，余挺，李永红，等 .300m级高土石心墙坝蠕变特性研究［J］.岩土工程学报，2014，36（1）：140-145.

［12］徐晗，黄斌，饶锡保，等 .三轴试样钻孔灌砂固结排水效果试验研究［J］.岩土力学，2009，30（11）：3242-3248.