Visual Basic语言循环结构的可视化教学案例研究

林温阳

Visual Basic（以下简称VB）语言程序设计教学概念多、算法繁、涉及面广，特别是循环结构语句算法部分，传统课堂枯燥乏味的语言文字讲授和PPT演示方法，很难直观地再现其动态性与逻辑性，让人感觉抽象不易理解，这给初学程序设计的高中生带来了很大障碍。笔者在教学实践中尝試采用画流程图（或NS图）、动画模拟、绘制二维解析图、构建思维模型等可视化教学策略，让抽象概念、程序执行过程和算法设计可视化，较好地培养了学生的计算思维能力。

● 绘制VB循环结构流程图（或NS图）

VB循环结构分计数型和条件型两类，笔者绘制流程图（或NS图），以表格形式综合类比For…Next、Do…Loop、While…Wend三种循环语句形式的基本特征和适用范围，运用奥苏贝尔提出的先行组织者教学策略，让学生在弹性课堂预设的情境中形成一个图式化思维表象，提供富有意义的学习材料便于学习者利用已有认知图式同化新知。[1]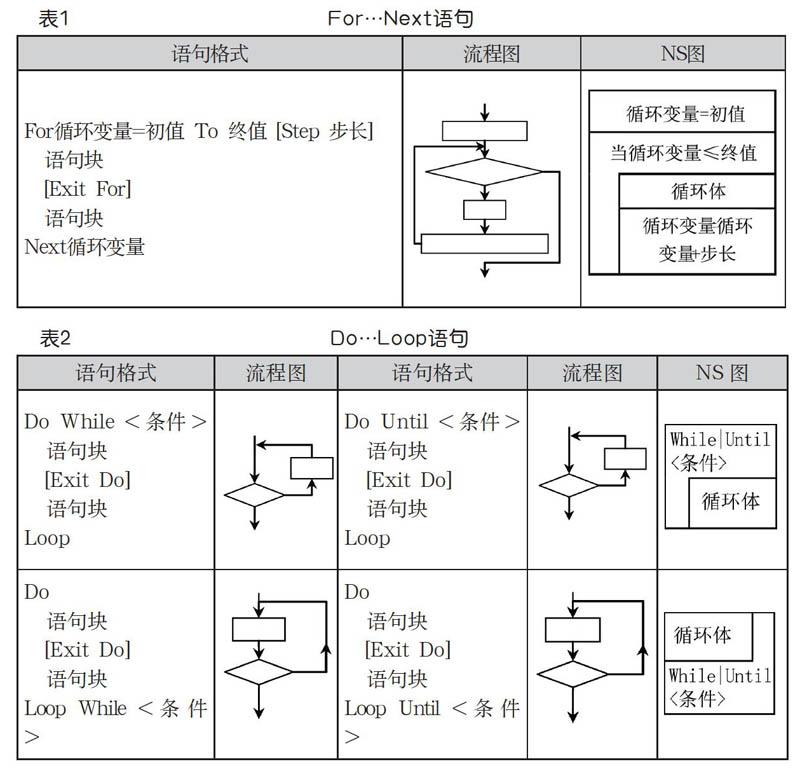

1.For…Next语句

“For循环”属于计数型循环，通过在已知循环次数前提下执行循环体，循环体的重复执行次数是由循环控制变量的初值、终值和步长值（可以是正值或负值）共同决定的。For循环语句格式、流程图、NS图如表1所示。

2.Do…Loop语句

“Do循环”属于条件型循环，一般适用于解决无法预知循环次数的问题，其构造形式相对灵活。既有指定循环进入条件的“While当型循环”，又有指定循环终止条件的“Until直到型循环”。按照判断循环条件的顺序不同，又有前测型循环结构和后测型循环结构之分。前者是先判定条件，后者是先执行循环体语句，或循环一次后再来判定条件，根据条件决定是否继续执行循环体。Do循环语句格式、流程图、NS图如上页表2所示。

3.While…Wend语句

“While循环”属于条件型循环，若条件判断满足时执行循环体，否则跳出循环体直接执行Wend之后的语句，与前述Do While…Loop语句相似。While循环语句因为没有自动修改循环条件的功能，在其循环体内通常必须有改变循环控制条件的语句，否则会致使循环无法正常结束，从而陷入“死循环”。While循环语句格式、流程图、NS图如表3所示。

● 动画模拟VB循环程序执行

循环语句既是程序设计学习的一大难点，同时也是其魅力所在。借助“程序框图”学生掌握了循环结构的基本概念，但对循环程序执行过程的理解，刚开始时往往会迷失在一大段令人费解的程序代码中，尤其是面对像嵌套、递归和迭代等复杂的循环结构问题（如字符图形打印、冒泡排序、汉诺塔问题等体现循环思想的经典题型），常常因缺乏相关生活经验，又无法进行现场观察体验，难以发挥想象力和逻辑推理能力，致使无法有效地将新知与已有认知结构中的旧知建立起实质性联系，从而给学习带来很大障碍。[2]即便教材中有大篇幅的文字描述和静态图解，大多数学生看过之后，还是懵懵懂懂，无法正确判读VB程序的源代码。

澳大利亚认知心理学家约翰·斯威勒（J.Sweller）提出的认知负荷理论认为，当现有学习材料的复杂性超过学习者的前期知识水平和认知承载能力时，学习就会陷入困境。此时，需要采用越级捷径式直觉思维方式表征知识单元，引导和帮助学生发展认知。笔者通过动画视频模拟及交互式多媒体软件进行直观具象的屏幕演示与速度可控的互动模拟操作，从而成功创设仿真体验式教学情境，这样学生可以清楚地“看见”程序的复杂算法结构和每一步执行过程，帮助他们从繁琐的循环步骤中解放出来，集中精力挖掘隐含的循环算法模型，加深对循环问题的本质理解。

● 绘制二维解析表跟踪程序数据

在VB程序设计循环结构教学中，笔者通过绘制二维解析图进行数据变换，将VB源代码映射为数据表，跟踪程序数据与指令代码的动态执行过程，校验VB循环控制变量值的起止阈值与增量变化，实现了程序动态执行过程的可视化。这是读懂VB程序源代码的基本方法，也是快速求解VB循环应用问题的基本技巧。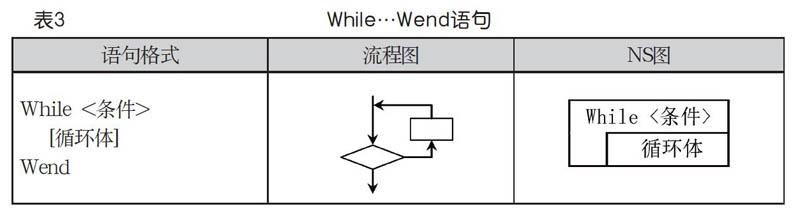

题例：程序运行显示结果是

。

Private Sub Form_Click（）

Dim i as Long

S=1

For i=5 to 8

S=S+1

Next i

Print S

End Sub

题例解析：提取循环控制变量i和因变量S，绘制四象限二维解析表（如表4），按①→②→③→……→⑨顺序依次填写，根据二维解析表可以直观地看出程序运行结果为5。结合VB单步调试功能，在图形用户界面中输入响应事件的参数，亦可清晰地反映程序执行流程和数据更新变换。[3]

美国著名学者爱德加·戴尔（Edgar Dale）提出的“学习金字塔”理论指出，学习者通过自己动手和同伴互助方式，主动参与、积极有效地发现学习，在定向模仿和练习操作中将内潜性、观念性的心智技能外显化，有助于他们由具体到抽象逐步地建立稳定清晰的视动觉。现代心理学研究也表明知识获取是一个层级式视知觉加工分析的过程，随着层级的提升它变得越来越具体和精确。[4]为了进一步强化和巩固学生对循环结构语句的理解，笔者在此安排了两个变式问题综合训练，让学生在多维进阶任务及题型变式训练中类比分析、逐层推进，学习绘制二维解析表，加深对循环体执行过程和循环变量的理解，从而准确得出循环程序运行结果。

变式一：程序运行输入274，显示结果是__________。

Private Sub Form_Click（）

Dim i as Long

i=inputbox（"请输入一个正整数"）

While i<>0

j=i mod 10

t=t+j

i=i＼10

Wend

Print t

End Sub

題例解析：在单重循环中提取循环控制变量i和因变量j、t，使用四象限二维解析表（如表5），得出运行结果为13。

变式二：程序运行显示结果是

。

Private Sub Form_Click（）

Dim i，j，a as Long

for i= 1 to 3

for j= 1 to i

a=a+1

next j

next i

Print i，j，a

End Sub

题例解析：在多重嵌套循环中提取循环控制变量i、j和因变量a，内循环和外循环层次要分清，确保不交叉。使用四象限二维解析表（如表6），得出运行结果为4、4、6。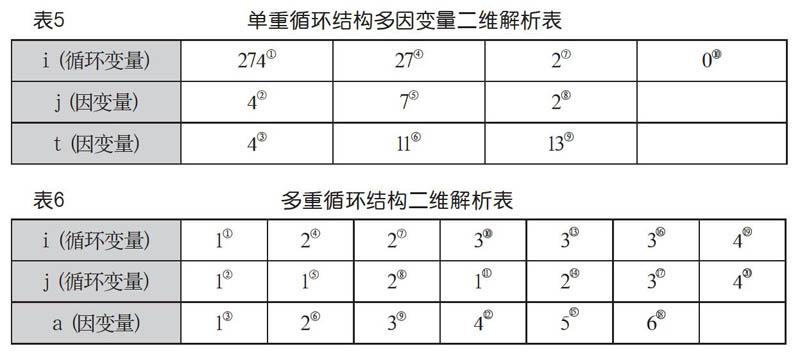

● 借助直观思维模型构建知识图谱

思维导图作为一款促进思维激发和辅助思维整理的非线性思维视觉化表征工具，它能为学习者将学习过程中原本不可视的思维方法和思考路径图式化地清晰呈现出来，从而有效帮助学习者建构主题知识网络图谱，理解知识点间的内在联系。[5]笔者使用如MindManager、FreeMind和Inspiration等思维导图工具软件可以轻松专业地绘制树状图、鱼骨图、路径图和时间线等主题图式，呈现学习认知组块，将学习思维加以可视化地整理提炼、重组展示，以此成功激活学生已有认知图式和全部感知力，还原思维本性。具体操作步骤如下：①确定主题，运用曼陀罗九宫格法激发头脑风暴，协同团队智慧逐级细化直至明析问题要点；②应用关键词、色彩对比、分支图式等梳理知识间网络化脉络关联，将零散知识加以全景性概括重组；③依托网络学习平台虚拟社区，组织学生线上编程作品展示、评价与反思，提升他们主动参与学习的积极性和课堂生成性学习成果的认知度。

笔者结合《VB循环结构》教学内容，绘制思维导图的重点在于让学生明白解决哪些类型问题适合采用循环结构算法，以及应当采用哪种循环结构语句来解决问题，让学生熟练掌握循环结构程序设计的基本思路，从而培养他们的计算思维，使其学会运用计算机科学的基础概念去求解问题和设计系统。[6]

● 可视化教学效果评价分析

笔者借助基于大数据挖掘技术的可视化教学评价系统，实时准确地将学生自测自评、组评师评的量化评价结果图形化显示，并加以指标间趋势关联分析，为课堂教学及时提供反馈，帮助师生深入观察、分析和诊断隐含的教学问题，发掘有益的教学规律，并结合绩效支持手段监控学生的课堂学习行为，可整体上调节教学进程，从而达到预定的教学目标。

笔者随机选择一个实验班与一个对照班作为一组独立样本数据进行对比实验及差异评估，经Z检验统计法测试显示两班学生原本在学习起点和学习能力指标上无显著性差异。在实验班教学中应用了可视化教学策略之后，实验班与对照班学生的整体学习成绩对比差异非常显著，且反映数据离散程度的实验班学生成绩标准差比对照班小（如上图）。实验结果评估表明，在VB循环结构教学中应用上述可视化教学策略已取得了良好的教学效果，有利于全体学生的均衡发展。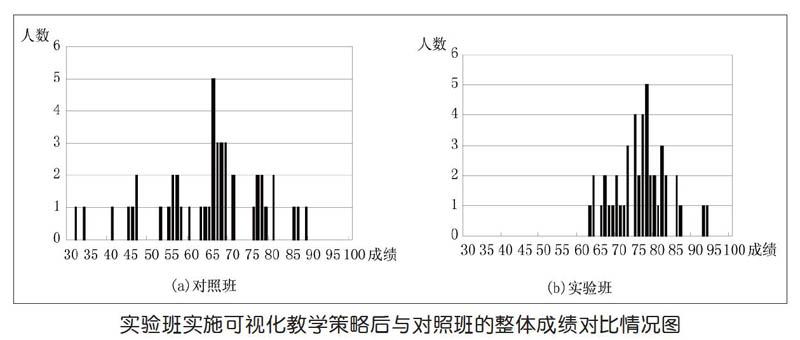

● 结束语

当前教育领域新媒体新技术广泛运用，动画模拟、人机交互、虚拟现实及增强现实（Augmented Reality，简称AR）提供了强大技术支撑，它们所带来的学习体验让教学真正进入了“读图”和“影像”的视觉时代，在教育教学中应用可视化教学方式越来越受广大师生欢迎。可视化教学方式在不增加学习者认知负荷的同时，将复杂抽象的概念、原理、过程和方法以图式化视觉思维模型为表征，通过图表、图解、图形、表格、地图、列表等道格纽瑟姆（D.Newsom）所概括的静态信息，以及内容形象、时空连续的视音频动态信息（如微视频）图解承载知识，并直观地呈现给学生，帮助他们建立整体具象的认知，避免了纯文字说教，让他们能更愉悦、有深度地感知分析、建模解决复杂问题。

参考文献：

[1]申石磊，季超.Visual Basic程序设计基础[M].北京：高等教育出版社，2010：119-131.

[2]严蔚敏，吴伟民.数据结构[M].第二版.北京：清华大学出版社，2013：48-52.

[3]瞿中，刘玲，熊安萍.计算机科学导论[M].第四版.北京：清华大学出版社，2014：278.

[4]艾森克.认知心理学[M].高定国，译.第五版.上海：华东师范大学出版社，2009：50-51.

[5]赵国庆.概念图、思维导图教学应用的若干重要问题的探讨[J].电化教育研究，2012（5）：78-84.

[6]周以真.计算思维[J].美国计算机学会通讯，2007（11）：33-35.