基于HPA非线性的大规模MIMO预编码算法

王 军，戴建新，程崇虎，汪 鹏，李 莎

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003；2.南京邮电大学 理学院，江苏 南京 210023)

基于HPA非线性的大规模MIMO预编码算法

王 军1，戴建新2，程崇虎1，汪 鹏1，李 莎1

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003；2.南京邮电大学 理学院，江苏 南京 210023)

大规模MIMO具有较高的能量效率和频谱利用率等优点，但由于廉价的硬件使用也会带来一些问题，比如高功率放大器非线性等。当高功率放大器工作在非线性区域时，放大后信号的幅度和相位都会产生误差，从而使得用户接收到的信号与期望信号产生误差，降低了系统的性能。研究了当高功率放大器非线性时，传统预编码算法的不足之处。然后，根据传统算法的不足与非线性的高功率放大器对信号的影响，提出一种改进的预编码算法。通过仿真结果可以看出，该算法相对块对角化预编码算法和迫零预编码算法在误码率和容量性能上有着显著提高，尤其是在高信噪比的场景下优势更佳。因此可以得出结论，该算法能够降低高功率放大器非线性对系统性能的影响。

大规模MIMO；高功率放大器；预编码算法；误码率；非线性

1 概 述

为了解决人们对服务质量和数据速率的需求不断提高的问题，提出了一些新的无线通信技术，其中大规模MIMO(Multiple-Input Multiple-Output，多输入多输出)技术扮演着重要角色。而且，大规模MIMO技术是下一代移动通信系统中的关键技术之一，其使中心基站或者分布式基站装有上百根天线，从而大大提高了通信速率和服务质量[1-4]。

虽然大规模MIMO具有很多优点，但是其因为基站天线的增多也会对系统性能带来一定的限制。其中之一就是HPA(High-Power Amplifier，高功率放大器)的非线性问题[5]。HPA是无线通信系统的一个重要模块，通常为了简化系统性能分析和系统设计，都假设HPA工作在线性区域。然而，实际上HPA有可能工作在非线性区域，尤其是中高功率信号。如果HPA工作在非线性区域，那么其对发射信号会引起失真，包括幅度和相位失真[6]。

非线性的HPA有两种模型：无记忆的频率平坦模型和有记忆的频率选择模型[7]。其中，无记忆的HPA模型具有幅度到幅度和幅度到相位转换的特点，例如TWTA(Travelling Wave Tube Amplifier，行波管功率放大器)[8]、SSPA(Solid-State Power Amplifier，固态功率放大器)[9]模型和SEL(Soft-Envelope Limiter，软包络限制器)模型[10]。有记忆的HPA模型有Volterra、Wiener和Hammerstein[7]。

近些年，对于MIMO通信系统中存在的HPA非线性问题，人们也做出了很多努力。例如，文献[6]利用空时块编码分析HPA非线性对系统性能的影响。文献[11]利用空时编码分析了HPA非线性对MIMO系统的SEP(Symbol Error Probability，误码率概率)的影响。另外，由于HPA非线性，以往的MRC(Maximal Ratio Combining，最大比合并)对系统的性能有所下降，因此文献[12]提出了一种QEGT(Quantized Equal Gain Transmission，量化等增益波束)方案。然而通过研究预编码方案来弥补HPA非线性问题，还是一个比较新颖的想法。

文中分析了HPA非线性对基站发射信号的影响，探讨在HPA非线性时传统的预编码方法存在的问题，比如BD(Block Diagonalization pre-coding，块对角化)预编码和ZF(Zero Forcing，迫零)预编码方法[13-14]，针对这一问题提出一种改进的预编码方案。仿真结果表明，该改进算法弥补了HPA非线性对系统的影响。当HPA工作在线性区域时，该算法和传统算法性能相当。当HPA工作在非线性区域时，该算法优于传统算法。

2 系统模型

图1中，Hk∈Mk×N是第k位用户的信道矩阵，其每个元素都是均值为0、方差为1的高斯复随机变量。W∈N×M是所有用户的预编码矩阵，不同的预编码方案会得到不同的预编码矩阵。sk∈Mk×T是第k位用户在预编码前的信号向量，T代表信号向量的长度。Gk∈Mk×Mk是第k位用户的信号检测矩阵。由此，当HPA工作在线性区域时，可以得出用户接收信号Y=[y1,y2,…,yk]T：

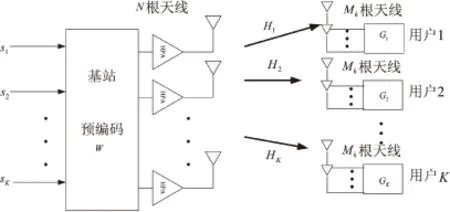
图1 系统模型

Y=HWs+n=HX+n

(1)

其中，H=[H1,H2,…,Hk]T表示所有用户的信道向量矩阵；X∈N×T是编码后的信号矩阵；n∈M×T表示用户侧的噪声，且其每个元素都是均值为0、方差为σ2的高斯复随机变量。

在信号传输过程中，已调制后的信号由HPA放大后，再发射出去。在实际的场景下，HPA有可能工作在非线性区域，因此就会对信号的幅度和相位造成一定的失真。把调制后的信号改成极坐标形式，如下：

sin=rejθ

(2)

其中，r和θ分别代表信号的幅度和相位，并且j2=-1。

则通过非线性的HPA之后，信号可以表示为：

sout=fA(r)ej fP(r)ejθ

(3)

其中，fA(·)和fP(·)分别为AM/AM(amplitude-to-amplitude，幅度到幅度)和AM/PM(amplitude-to-phase，幅度到相位)的一种转换式。

下面，文中会列出三种无记忆的HPA模型转换式，主要研究第一种模型。

第一种是TWTA，其AM/AM和AM/PM函数式为[8]：

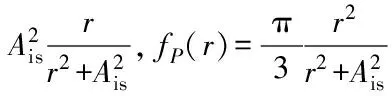
(4)

其中，Ais为输入电压。

第二种为SSPA模型，其AM/AM和AM/PM函数式为[9]：

(5)

其中，Aos为输出电压；β为转换因子。

第三种是SEL模型，其AM/AM和AM/PM函数式为[10]：

(6)

为了分析简单，假设基站所有的信号发射支路的HPA非线性对信号有着相同的影响，且基站和用户侧已知HPA参数。则当HPA工作在非线性区域时，可以得到用户接收信号Y=[y1,y2,…,yk]T：

Y=HU+n

(7)

其中，U∈N×T为预编码之后信号经过HPA的输出信号矩阵。

根据式(3)，可以得到uij(i=1,2,…,N,j=1,2,…,T)。

uij=fA(|xij|)exp[j(θij+fP(|xij|))]

(8)

其中，uij和xij分别是U和X在第i行第j列上的元素值；θij是元素xij的相位。

由式(8)可以看出，非线性的HPA对发射信号产生了一定的影响。

3 改进的预编码算法

本节介绍了BD和ZF二种传统预编码，然后分析了当HPA工作在非线性区域时，这二种预编码算法所表现出来的不足，并针对其不足之处，提出一种改进的预编码算法。

3.1 传统的预编码算法

由文献[15]可知，当HPA工作在线性区域时，第k位用户BD预编码矩阵为：

(9)

(10)

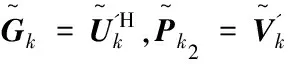
(11)

然而，如果HPA工作在非线性区域，预编码后信号Pks在经过HPA后，其矩阵元素将变成：

(12)

因此，经过非线性的HPA后，BD预编码算法将不能消除用户间的干扰，同时也不能将用户有效信道分解成平行子信道，从而降低了性能。

第二种传统的预编码算法就是ZF编码方案[13]，其预编码矩阵为：

WZF=HH(HHH)-1

(13)

由此可得，用户接收信号矩阵为：

Y=HWZFs+n=HHH(HHH)-1s+n=s+n

(14)

当HPA工作在非线性区域时，通过ZF预编码后的信号经过HPA放大后输出：

(15)

因此，ZF预编码和BD预编码一样，当HPA工作在非线性时，其性能都有所下降。

3.2 LBD和LZF预编码方法

针对上述传统预编码方案不能解决非线性HPA带来的问题，文中通过研究非线性HPA对信号的影响，提出一种改进方法。

由式(8)可得当HPA工作在非线性区域时，发射信号为：

(16)

从上式可以看出，预编码后的信号通过非线性的HPA后，会多出一个系数因子dij，其值大小表示非线性HPA对信号的影响程度。

可以得出接收信号矩阵Y的第l(l=1,2,…,M) 行第l1(l1=1,2,…,T) 列上的元素值为：

(17)

其中，hll3为矩阵H的第l行第l3列上的元素。

由式(17)可以清楚地看出，只要能够抵消系数因子dl3l2，那么就能弥补因HPA非线性带来的损失，而由式(3)和式(16)，可以构造一个系数因子关于信号模长的函数：

(18)

其中，x'为大于0的实数。

为了分析方便，假设输入电压Ais=1，则对函数y'的仿真如图2所示。

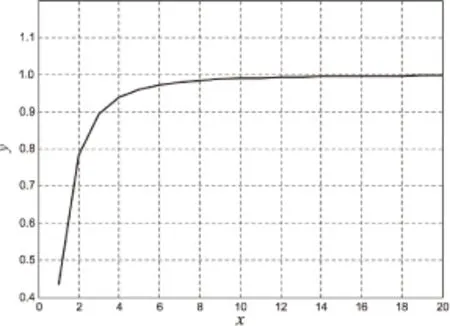
图2 系数因子d关于信号模的曲线图

从图2可以看出，函数y'是递增的，且当x'大于16时，y'的值逐渐趋于1，也即系数因子也趋于1。可以从此入手，对传统预编码矩阵乘上一个线性化因子1/α，当α大于16时，系数因子就会趋于1，从而抵消掉因HPA非线性对通信系统的影响。那么，预编后的信号通过非线性的HPA后有：

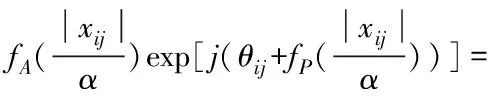
(19)

通过上式得出，当α≥16，式(7)就等于式(3)。至此，可以通过这种方法消除HPA非线性的影响。

针对不同的预编码方法，可以得到改进的方案。比如，LBD(LinearBD，线性块对角化)的预编码矩阵WLBD=WBD/α，LZF(LinearZF，线性迫零)的预编码矩阵为WLZF=WZF/α。之所以被称为线性化，主要是因为其解决了非线性的HPA对系统的影响。

4 数值仿真

对文中算法的性能进行仿真验证，并与ZF、BD预编码算法作比较。仿真参数为：基站天线数N=100，用户数K=50且每个用户都是两根天线，α=20，Ais=1，信噪比定义为PT/σ2，误码率是基于正交相移键控(QuadraturePhaseShiftKeying，QPSK)的调制方式计算得到的。

当HPA工作在非线性区域时，文中算法和其他算法在误码率上的比较见图3。

图3 文中算法与传统方法在误码率上的比较

从图中可以明显看出，文中算法优势明显，且信噪比越大，其优势越明显。因此，文中算法在误码率上弥补了非线性HPA对系统的影响。

当HPA工作在非线性区域时，文中算法和其他算法在和速率上的比较见图4。

图4 文中算法与传统方法在和速率上的比较

从图中可以看出，文这算法较好地改善了非线性HPA对系统的影响。

5 结束语

针对大规模MIMO系统中存在的非线性HPA的问题，分析了其对系统的影响，尤其是中高功率信号对发射信号带来的失真。针对传统预编码算法所表现出来的不足，提出一种改进方法。仿真结果表明，文中算法具有很好的性能，有效地弥补了HPA非线性对系统性能的影响。同时，该方法也有待进一步研究，比如基站天线小于用户总天线情况和基站有非完全信道信息时的场景。

[1]LuL,LiG,SwindlehurstAL,etal.AnoverviewofmassiveMIMO:benefitsandchallenges[J].IEEEJournalofSelectedTopicsinSignalProcessing,2014,8(5):742-758.

[2]RusekF,PerssonD,LarssonEG,etal.ScalingupMIMO:opportunitiesandchallengeswithverylargearrays[J].IEEESignalProcessingMagazine,2012,30(1):40-60.

[3]LarssonE,EdforsO,TufvessonF,etal.MassiveMIMOfornextgenerationwirelesssystems[J].IEEECommunicationsMagazine,2014,52(2):186-195.

[4]LamareRC.MassiveMIMOsystems:signalprocessingchallengesandfuturetrends[C]//URSIradiosciencebulletin.[s.l.]:[s.n.],2013:183-188.

[5]HakkarainenA,WernerJ,DandekarKR,etal.Widely-linearbeamformingandRFimpairmentsuppressioninmassiveantennaarrays[J].JournalofCommunicationsandNetworks,2013,15(4):383-397.

[6]QiJ,AïssaS.OntheeffectofpoweramplifiernonlinearityonMIMOtransmitdiversitysystems[C]//IEEEinternationalconferenceoncommunications.[s.l.]:IEEE,2009:1-5.

[7]GregorioFH.Analysisandcompensationofnonlinearpoweramplifiereffectsinmulti-antennaOFDMsystems[D].Helsinki:HelsinkiUniversityofTechnology,2007.

[8]SalehAAM.FrequencyindependentandfrequencydependentnonlinearmodelofTWTamplifier[J].IEEETransactionsonCommunications,1981,29(11):1715-1720.

[9]RappC.EffectsofHPA-nonlinearityona4-DPSK/OFDM-signalforadigitalsoundbroadcastingsignal[C]//Europeanconferenceonsatellitecommunications.[s.l.]:[s.n.],1991:179-184.

[10]RoweHE.MemorylessnonlinearitieswithGaussianinputs:elementaryresults[J].BellLabsTechnicalJournal,1982,61(7):1519-1526.

[11]SulymanAI,IbnkahlaM.PerformanceofspacetimecodesovernonlinearMIMOchannels[C]//EighthinternationalsymposiumonsignalprocessingandITSapplications.[s.l.]:[s.n.],2005:407-410.

[12]QiJ,AissaS.ImpactofHPAnonlinearityonMIMOsystemswithquantizedequalgaintransmission[C]//Internationalsymposiumonpersonal,indoorandmobileradiocommunications.[s.l.]:[s.n.],2009:2891-2895.

[13]PeelCB,HochwaldBM,SwindlehurstAL.Avector-perturbationtechniquefornear-capacitymultiantennamultiusercommunication-partI:channelinversionandregularization[J].IEEETransactionsonCommunications,2005,52(1):195-202.

[14]SpencerQH,SwindlehurstAL,HaardtM.Zero-forcingmethodsfordownlinkspatialmultiplexinginmultiuserMIMOchannels[J].IEEETransactionsonSignalProcessing,2004,52(2):461-471.

[15] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.

Linear Precoding in Massive MIMO Based on Nonlinear High-power Amplifier

WANG Jun1，DAI Jian-xin2，CHENG Chong-hu1，WANG Peng1，LI Sha1

(1.College of Telecommunications & Information Engineering,Nanjing University of Posts and Telecommunications，Nanjing 210003,China； 2.School of Science,Nanjing University of Posts and Telecommunications，Nanjing 210023,China)

Large scale MIMO has the advantages of high energy efficiency and spectrum utilization,but it also brings some problems because of cheap hardware use,such as high power amplifier nonlinearity,etc..When the high power amplifier in the nonlinear regime,the amplitude and phase of amplified signal will produce error,thereby leading to the errors of signal and the desired signal received by users and reduce the performance of the system.The deficiency of the traditional precoding algorithm is studied when the high power amplifier is nonlinear.An improved pre-coding algorithm is presented according to the impact of traditional algorithm and nonlinear high power amplifier on the signal.The simulation results show that the algorithm is improved significantly in bit error rate and capacity performance compared with block of diagonalization pre-coding algorithm and forced zero pre-coding algorithm,especially better in the scene of high signal to noise ratio.So it is concluded the algorithm is able to reduce the influence of nonlinearity of high power amplifier on the performance of the system.

massive MIMO;HPA;pre-coding algorithm;bit error rate;nonlinear

2016-03-07

2016-06-15

时间：2017-01-04

江苏省博士后科研资助计划(1501073B);南京邮电大学自然科学基金(NY214108)

王 军(1991-)，男，硕士生，研究方向为大规模MIMO系统中的预编码；戴建新，博士，副教授，研究方向为5G移动通信系统的关键技术；程崇虎，博士，教授，研究方向为电磁场。

http://www.cnki.net/kcms/detail/61.1450.TP.20170104.1028.044.html

TN929．5

A

1673-629X(2017)01-0034-05

10.3969/j.issn.1673-629X.2017.01.008