基于图论的AD和EMCI脑功能网络分析

唐 进，马千里

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

基于图论的AD和EMCI脑功能网络分析

唐 进，马千里

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

人脑是一个复杂的系统，各个脑区神经活动之间相互作用。对脑功能网络的研究，一方面有助于探索大脑神经活动机制，另一方面，对探索大脑相关疾病的发病机理具有重要的应用价值和意义。采集了38例正常人(NC)、25例阿尔兹海默症(AD)患者、42例早期轻度认知障碍(EMCI)患者在静息状态下功能磁共振成像数据，利用标准脑模板将全脑划分为90个感兴趣区域，提取每个脑区的时间序列值，并计算脑区之间的相关程度。随后，在相对阈值法的基础上，提出了一种绝对阈值的方法。结合这两种不同的阈值选取策略，对所有被试的脑功能连接网络进行了建模，分别计算了平均最短路径长度L和聚类系数C。结果表明，AD和EMCI患者的脑功能连接网络的小世界性质已发生了变异。

静息状态功能磁共振成像；感兴趣区域；时间序列值；阈值选取策略

0 引 言

近年来，随着人口老龄化的不断加剧，阿尔兹海默症的比例大幅上升，并有愈演愈烈之势。阿尔兹海默症不仅侵蚀老年群体的健康，也给年轻一代增添了沉重的负担。人的大脑是一个复杂系统[1]，目前对大脑的理解和认识还远远不够。fMRI综合了解剖、功能、影像三种因素[2]，使磁共振临床诊断从单一形态学研究向功能相关的系统研究发展转变。功能磁共振成像技术[3]和复杂网络理论[4]的日益成熟，为揭开大脑奥秘提供了有力的手段和坚实的理论基础。一直以来，早期轻度认知障碍患者都是阿尔兹海默症的高发人群，因此研究NC组、AD组以及EMCI组之间的脑功能连接网络差异，对于探索阿尔兹海默症的发病机理，以及预防和治疗阿尔兹海默症，具有重要的应用前景和现实意义。

目前，有很多EMCI和AD疾病相关的脑功能连接网络[5-6]的研究。例如，柯铭等[7]基于复杂网络理论，研究了静息状态下健康志愿者被试的体素之间的功能连接关系，考察他们脑功能网络的结构和拓扑特性，结果显示，网络具有小世界性质和无标度特性。王湘彬等[8]基于矩阵稀疏度阈值法，计算了正常老年人NC和EMCI患者脑功能网络的聚类系数和平均路径长度，发现EMCI患者脑功能网络的小世界属性[9]与正常人相比有所增强，但某些阈值下的对比效果不明显。Supekar等[10]通过对比年龄相同的正常人，发现AD患者脑功能网络也呈现小世界属性。Lee等[11]运用图形稀疏字典和推理分析的方法，提取了正常NC组，CDR0.5(Clinical Dementia Rating scale)、CDR1.0、CDR2.0的AD患者组的DMN(Default Mode Network)，发现得到的默认脑功能网络与疾病程度紧密相关。这些研究成果均表明，人脑可以抽象为网络，并且网络属性会随着脑疾病发生而改变。

文中在统一标准下分析了NC、EMCI、AD组的脑功能网络拓扑性质的差异，结合固定稀疏值的阈值选取方法，提出一种新的绝对阈值的方法。该方法计算简单、效果显著。相对阈值法和绝对阈值法各有所长、相互补充，很好地再现了各组被试之间的真实差异，实验结果更加可靠、可信。

1 数据采集与预处理

根据前人研究经验[12]，文中使用的所有静息状态下的fMRI数据全部来自于阿尔兹海默症神经影像学(Alzheimer’s Disease Neuroimaging Initiative，ANDI)数据库。该数据库由多家权威机构联合成立，包括美国国家老年化研究所、美国国家生物医学成像和生物医学工程研究所、美国食品和药物管理局等。所有被试的性别、年龄等信息如表1所示。采集到的原始fMRI数据往往包含大量的噪声等不确定干扰因素，所以需要对数据做进一步的预处理[13]。文中借助SPM8(Statistical Parametric Mapping)软件对原始数据进行时间层校正、头动校正、空间归一化、平滑、去除线性漂移、滤波等处理，最后得到具有生理意义的静息状态全脑fMRI数据，为后续脑功能连接网络的构建打下了基础。

表1 EMCI、NC和AD被试的基本信息

2 网络建模方法

2.1 阈值选取策略

阈值，也就是临界值，实验中通过设置阈值将弱的连接去掉，同时将大于阈值的强的连接关系保留，对应的脑区之间认为有边连接。阈值的选取一向比较灵活，也没有统一的标准。该实验在相对阈值法的基础上，采用了新的绝对阈值法。其方法过程如下：

1)相对阈值法。

相对阈值法的基本思想是通过设置固定稀疏值将网络中强的连接关系保留，并去除弱的连接关系。实验中，固定稀疏值定义为邻接矩阵中1的个数除以全部矩阵元素个数。文中设置了一系列不同稀疏值来观察各组被试的脑功能网络，所有固定稀疏值的设定需要满足以下原则：

(1)全脑功能网络是连通的，没有孤立节点；

(2)网络的平均度值大于2lnN，N是节点个数；

(3)全部被试脑功能网络具有小世界性质，即σ>1.1。

最终，选取的固定稀疏值s的取值范围为[0.12，0.4]，间隔为0.02。

2)绝对阈值法。

绝对阈值法的基本思想是设置一个固定值m，只保留相关系数矩阵中大于m的元素，这些元素在构建网络时当作有边连接。由相对阈值法的分析可知，要保证满足上述三条原则，每个被试的脑功能网络密度在0.12～0.4之间即可。NC组全部被试稀疏值边界处的绝对阈值如图1所示。

图1 NC组s=0.12，s=0.4时的绝对阈值

要保证每个被试的网络稀疏值在0.12和0.4之间，由图1可知，NC组绝对阈值范围为：0.195 4≤m≤0.283 2。

图2描述了AD患者组的绝对阈值情况。

同NC组一样，要想网络的稀疏度在0.12和0.4之间，可得AD组的绝对阈值取值范围为：0.184 3≤m≤0.263 7。

图3反映了EMCI组的绝对阈值大小。

图2 AD组s=0.12,s=0.4时的绝对阈值

图3 EMCI组s=0.12,s=0.4时的绝对阈值

同理可得，EMCI组绝对阈值的范围为：0.198 4≤m≤0.280 3。

最终的绝对阈值m应是以上3组m值的交集，由此可得，绝对阈值范围为：0.198 4≤m≤0.263 7。为了计算方便，选取绝对阈值m的范围为[0.2，0.26]，间隔为0.01。

2.2 邻接矩阵构建

邻接矩阵是最简单最常见的计算机中表示图的方法，文中借助AAL[14]标准脑模板将大脑划分为90个脑区，以脑区时间序列之间的同步性表示脑区间的功能关系[15]，脑区之间的相关程度采用皮尔逊偏相关系数[16]进行度量，然后通过计算可得一个偏相关系数矩阵。偏相关系数的计算方法有多种，文中采用一种基于皮尔逊相关系数计算皮尔逊偏相关系数的经典方法。首先，计算全部脑区BOLD(Blood Oxygen Level Dependent)时间序列矩阵X的协方差矩阵R，然后求出R的逆协方差矩阵r，最后进一步计算脑区之间的偏相关系数，公式如下：

R=Cov(X)

(1)

r=(rij)=(R)-1

(2)

(3)

偏相关系数介于-1和1之间，其绝对值反映了脑区之间功能连接的强弱程度，绝对值越大，表明脑区间的相关程度越强，绝对值接近0时，相关程度很弱，或者可以理解为几乎没有相关性。偏相关系数的符号决定了相关关系的正负性，正相关的脑区之间相互促进，而负相关的脑区之间表现出明显的抑制作用。实验不考虑相关关系的方向性和正负性以及自相关，对偏相关系数矩阵进行了去对角线元素、绝对值化处理。然后分别基于相对阈值法和绝对阈值法对偏相关系数矩阵作二值化，得到所有被试脑功能连接网络的邻接矩阵。

2.3 拓扑指标计算

基于图论的理论基础，对所有研究对象都进行了脑功能连接网络的建模。从全局网络属性的角度出发，计算了平均最短路径长度和聚类系数，其定义如下：

(1)平均最短路径。

网络中节点i和j之间的最短路径也称为测地路径，是指连接这两个节点的边数最少的路径。节点i和j之间的距离dij定义为连接这两个节点的最短路径上的边的数目，也称为两个节点间的测地距离或跳跃距离。网络的平均最短路径长度L定义为任意两节点之间的距离的平均值，计算公式为：

(4)

其中，N为网络节点个数。

两点之间的最短路径可能不存在，可能只有一条、也可能有多条，但两点之间的距离是唯一的。如果两点之间存在最短路径，则两点之间的最短路径为有限值，若不存在最短路径，则最短路径长度为无穷大。

(2)聚类系数。

节点的聚类系数反映了其邻居节点的紧密程度，在图论中，局部聚类系数是网络中的局部节点倾向于聚集在一起的一种度量。节点i的局部聚类系数Ci定义为：

(5)

其中，ki为节点i的度值；Ei为节点i的ki个邻节点之间实际存在的边数。

网络的聚类系数是指全部节点局部聚类系数的平均值，反映了整个网络的集聚程度，定义如下：

(6)

3 实验结果

基于相对阈值法的阈值选取策略，在统一尺度下比较了NC、AD、EMCI三组被试的脑功能网络的平均最短路长度L和聚类系数C，结果如图4所示。

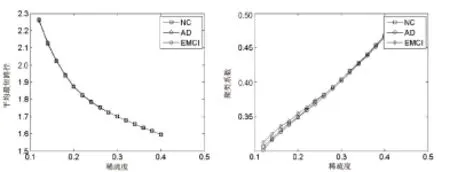
图4 相对阈值法NC、AD、EMCI的L和C

由图4可以看出，平均最短路径长度的3条曲线基本重合，说明NC、AD、EMCI各组的最短路径长度即使在不同的稀疏度下，都基本相等，可以认为它们之间几乎无差异。稀疏度越大，平均最短路径越短，脑区之间的信息交流越迅速便捷。仔细观察聚类系数曲线可以发现，在不同稀疏度水平下，与正常NC组相比，AD组的聚类系数偏小，而EMCI组的聚类系数却有所增大。聚类系数越大，说明脑区之间的紧密程度越高。

接着，又采取了绝对阈值法重复进行上述计算，得出的平均路径长度和聚类系数结果如图5所示。

图5 绝对阈值法NC、AD、EMCI的L和C

根据图5可知，AD组的平均最短路径长度最大，在不同的绝对阈值水平下，都明显高于正常老年人的标准，而EMCI的曲线和NC的曲线基本重合，也就是说EMCI的平均路径长度接近正常值。观察聚类系数可以发现，AD组的聚类系数最小，且全都明显低于正常NC组的水平；而EMCI组在绝对阈值小于0.23时，其聚类系数与正常人的水平差不多，当绝对阈值超过0.23时，随着阈值的增大，EMCI组的聚类系数明显高于正常值。对比图4与图5可以发现，绝对阈值法得出的网络属性差异更加明显。

4 结束语

文中主要借助图论工具和功能磁共振成像技术，探索了NC、AD和EMCI组的脑功能网络的拓扑性质。利用相对阈值法进行了网络建模，在此基础上提出了一种绝对阈值法的阈值选取策略，两种方法相互补充，取得了不错的实验效果。经过仔细分析比较发现，在实验的阈值设定区间内，NC、AD、EMCI组的全部被试的脑功能网络都满足小世界性质，但是存在显著差异，AD患者的小世界性质比正常人有所下降，脑区之间模块化整合能力不如正常人，而EMCI患者的小世界属性比正常水准有所加强。实验从两个不同角度进行网络建模，得到了相同的结果，该方法切实可行。文中提出的绝对阈值法效果要更好一些，实验成果对于临床上预防、治疗阿尔兹海默症具有指导意义。

[1]Zamora-LópezG,ZhouC,KurthsJ.Graphanalysisofcorticalnetworksrevealscomplexanatomicalcommunicationsubstrate[J].Chaos,2009,19(1):283-290.

[2]TurnerR,HowsemanA,ReesGE,etal.Functionalmagneticresonanceimagingofthehumanbrain:dataacquisitionandanalysis[J].ExperimentalBrainResearch,1998,123(1):5-12.

[3]LogothetisNK.WhatwecandoandwhatwecannotdowithfMRI[J].Nature,2008,453(7197):869-878.

[4]BounovaG,DeW.Overviewofmetricsandtheircorrelationpatternsformultiple-metrictopologyanalysisonheterogeneousgraphensembles[J].PhysicalReviewE,2012,85(2):1085-1088.

[5]RodriguezG，ArnaldiD，PiccoA.BrainfunctionalnetworkinAlzheimer'sdisease:diagnosticmarkersfordiagnosisandmonitoring[J].InternationalJournalofAlzheimer’sDisease,2011,2011:481903.

[6]PerazaLR，TaylorJP，KaiserM.DivergentbrainfunctionalnetworkalterationsindementiawithLewybodiesandAlzheimer’sdisease[J].NeurobiologyofAging,2015,17(9):2458-2467.

[7] 柯 铭,沈 辉,胡德文.基于fMRI的静息状态脑功能复杂网络分析[J].国防科技大学学报,2010,32(1):147-151.

[8] 王湘彬,赵小虎,江 虹,等.轻度认知功能障碍患者大脑fMRI网络小世界特性[J].中国医学影像技术,2014(5):790-793.

[9]WattsDJ，StrogatzSH.Collectivedynamicsof“small-world”networks[J].Nature,1998,393(6684):440-442.

[10]SupekarK，MenonV，RubinD，etal.NetworkanalysisofintrinsicfunctionalbrainconnectivityinAlzheimer'sdisease[J].PlosComputationalBiology,2008,4(6):1-11.

[11]LeeJ,YongJ,YeJC.Groupsparsedictionarylearningandinferenceforresting-statefMRIanalysisofAlzheimer'sdisease[C]//2013IEEE10thinternationalsymposiumonbiomedicalimaging.[s.l.]:IEEE,2013.

[12]NiH,ZhouL,NingX,etal.Exploringmultifractal-basedfeaturesformildAlzheimer'sdiseaseclassification[J].MagneticResonanceinMedicine,2016,76(1):259-269.

[13]GavrilescuM,StuartGS,HenshallK,etal.FunctionalconnectivityestimationinfMRIdata:influenceofpreprocessingandtimecourseselection[J].HumanBrainMapping,2008,29(9):1040-1052.

[14]Tzourio-MazoyerN,LandeauB,PapathanassiouD,etal.AutomatedanatomicallabelingofactivationsinSPMusingamacroscopicanatomicalparcellationoftheMNIMRIsingle-subjectbrain[J].Neuroimage,2002,15(1):273-289.[15]HampsonM,PetersonBS,SkudlarskiP,etal.DetectionoffunctionalconnectivityusingtemporalcorrelationsinMRimages.[J].PolymerDegradation&Stability,2002,15(4):247-262.

[16]SmithSM,MillerKL,GholamrezaSK,etal.NetworkmodellingmethodsforFMRI[J].Neuroimaging,2011,54(2):875-891.

Brain Functional Network Analysis of AD and EMCI Based on Graph Theory

TANG Jin，MA Qian-li

(College of Telecommunications & Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

The brain is a complex system of interactions between different brain regions activities.Researches on brain functional networks,on the one hand,help to explore the mechanism of the brain neural activity.On the other hand,it has important application value and significance to find the pathogenesis of brain related diseases.The collection of functional magnetic resonance imaging data in 38 Normal Controls (NC),25 Alzheimer's Disease (AD) patients and 42 participants with Early Mild Cognitive Impairment (EMCI) is carried on under resting state.The whole brain is divided into 90 regions of interest by using a standard brain template,extraction of time series of each brain region,calculation of their degree of correlation.Subsequently,on the basis of the relative threshold method,an absolute threshold is presented.Combined the two different threshold selection strategy,each subjects’ brain functional network is modeled.Average path length and clustering coefficient are considered,and eventually it shows that the small-world nature of AD and EMCI patients’ brain functional network have mutated.

rs-fMRI;regions of interest;time series;threshold selection strategy

2016-02-26

2016-06-15

时间：2016-11-22

国家自然科学基金资助项目(61201029)

唐 进(1991-)，男，硕士研究生，研究方向为无线通信与信号处理技术；马千里，副教授，研究生导师，研究方向为嵌入式系统软硬件设计、信号检测与处理、图像处理、生物医学电子学等。

http://www.cnki.net/kcms/detail/61.1450.TP.20161122.1227.034.html

TP

A

1673-629X(2017)01-0164-05

10.3969/j.issn.1673-629X.2017.01.037