基于脑电信号特征提取的睡眠分期方法研究

李 斐，马千里

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

基于脑电信号特征提取的睡眠分期方法研究

李 斐，马千里

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

睡眠分期是研究睡眠其及相关疾病的基础，是完成睡眠质量评估的前提，具有重要的意义。主要提出了一种新的脑电信号特征提取方法，能够有效提高睡眠分期的准确率。传统的自动睡眠分期方法都是以一个睡眠时期的时间片为单位进行特征参数提取，文中的睡眠分期按每30 s进行一次睡眠时期判断，将特征提取的时间片分为30 s、90 s、150 s以及210 s，研究不同时间片提取的特征参数对睡眠分期准确率的影响。采用Weka工具中的随机森林分类器对睡眠状态进行判别。实验结果表明，将210 s时间片得到的小波包系数、30 s时间片得到的排列熵以及90 s时间片得到的Petrosian分形维数作为自动睡眠分期的参数，可以得到85%的准确率；而采用30 s时间片得到的以上三类参数只能达到65%的准确率。

睡眠分期；脑电信号；小波包系数；排列熵；Petrosian分形维数

0 引 言

近年来，睡眠质量成为影响人类健康的隐形杀手，越来越多的人受到失眠等睡眠障碍的困扰。睡眠质量评估以及睡眠类疾病诊断成为研究热点。人体生理学表明，一个健康的深睡眠阶段可以加速物理疗养[1-2]。此外，健康的快速眼动(REM)阶段能够提高学习能力和记忆力。睡眠评分结果是所有睡眠问题识别中所必需的。睡眠评分，即为在多导睡眠图记录(PSG)中得出的睡眠分期。数据库中已经有部分病人的PSG样本，这其中就包括脑电图(EEG)、眼电图(EOG)和肌电图(EMG)数据[3]。1968年，专家遵循Rechtschaffen & Kales(R&K)规则，确定了评估PSG记录得出睡眠分期的规则。依据R&K准则，每个时期(30 s的数据)被分为清醒(W)、非快速眼动(N-REM S1，N-REM S2，N-REM S3和N-REM S4：从浅睡眠到深睡眠)和快速眼动(REM)。

目前，已经提出了许多用于睡眠阶段分类的模型[4]。下面列出了在文献中常用于从脑电图数据提取的特征参数，如标准偏差[5-6]、中位数[6-7]、算术平均值[7-8]、偏度[9-10]、峭度[9-10]、零交叉值[7,11]、方差值[7,12]、最大值和最小值[7,11]、平均能量[11,13-14]、平均teager能量[13]、彼得罗辛分形维数[14]、莱利熵[11,14]、频谱熵[11,14-15]、排列熵[16]、近似熵[17]、维格纳威乐系数[11-12]、小波变换[9,14,18-19]、平均曲线长度[13-14]、Hurst指数[17]和Hjorth参数[14,18]等。以上文献的特征参数提取时都按照一个睡眠时期(30 s的数据)进行计算，但在实际人工进行睡眠时期判断时，前后时间片的数据也会在专家的考虑范围内。

文中提出一种新的提取特征参数的方式，即将前后时间片(每30 s)也作为当前睡眠时期特征参数的提取依据。以脑电信号为睡眠分期原始信号，分别取30 s，90 s，150 s，210 s时间片的小波包系数、排列熵(PEn)、彼得罗辛分形维数(Petrosian分形维数)，从中提取特征参数作为中间30 s睡眠时期判断的依据。所提取的小波包系数、PEn、Petrosian分形维数作为睡眠各期特征参数组合，具有较高的分期准确率[20]。

1 数据来源

文中使用的数据集是由圣文森特大学医院和都柏林大学[21]提供，对数据库中全部25个人的数据进行研究。该数据的人口学特征如下：受试者25例，年龄：50±10岁，范围28～68岁；BMI：31.6±4.0 kg/m2，范围25.1～42.5 kg/m2；AHI：24.1±20.3，范围1.7～90.9。多导睡眠记录是通过Jaeger-Toennies系统获得。Jaeger-Toennies系统通过使用10～20个电极位置获得多导睡眠记录，其中包括了2个EEG通道(C3-A2和C4-A1)，2个EOG通道和1个EMG通道，平均记录时间为6.9 h。文中研究只采用单个脑电通道(C3-A2)，采样率为128 Hz。EEG信号主要集中在0～30 Hz处，且采用的脑电数据在50 Hz处具有工频干扰，通过5阶IIR巴特沃斯低通滤波器对EEG信号进行预处理，获得0～35 Hz的EEG信号。然后，对脑电图信号进行分割，分为30 s一个时期，每个时期对应于单个睡眠阶段。

表1显示了睡眠专家进行睡眠状态分类的25个受试者睡眠时期的分布，其中N-REM S1和N-REM S2期分别用N1、N2表示，且合并N-REMS3和N-REMS4期为N3期(即依据AASM准则分类)。

表1 睡眠状态各期分布

2 特征提取与分类方法

2.1 离散小波变换(DWT)

小波变换克服了傅里叶变换的缺陷[22]，并且该方法对于噪声不敏感，适用于非平稳信号的分析。连续小波变换的系数具有相当大的冗余量，为了在不丢失原始信号信息的情况下，尽量减小小波变换系数的冗余度[23]，提高压缩率[24]，引入了离散小波变换。定义如下：

(1)

其中，x(t)表示原信号；φ表示小波基。

DWT经常被用于分析EEG信号，主要问题是小波基以及分解层数的选择，其中小波分解的层数由原信号频率决定。分解层数的选择依据为使得被保留的小波系数与原信号不同睡眠状态的频率的相关性良好。脑电信号主要集中在0～30Hz，因此分解层数设置为4。在分解层数低于4层的情况下，会丢失低频段的信息。没有必要选择大于4的分解层，4层分解已经可以提取到所有EEG信号的有效频带。因此，信号被分解得到具有细节信息的D1-D4和含有低频信息的A4。

在相关的EEG信号研究中发现，与10阶Symmlet小波(sym10)和4阶Coiflet小波(coif4)比较，Daubechies小波具有更高的精度，并且注意到4阶Daubechies小波(db4)比2阶Daubechies小波(db2)略优[8,25-26]。所以，采用db4小波对EEG信号进行4层分解，并统计D2-D4与A4分量的绝对值的均值以及标准差。因为小波分解的特殊性，并不一开始就采用滑动窗进行小波分解计算90s，150s以及210s的参数，而是先计算30s时间片的小波系数，然后采用滑动窗以计算均值的方式得到90s，150s和210s的参数。

通过对EEG信号进行4层DWT分解获得的子带频率范围如下：A4分量包含δ频段(1～4Hz)，D4分量包含θ频段(4～8Hz)，D3分量包含α频段(8～13Hz)，D3分量包含β频段(13～30Hz)。D1分量具有高于30Hz的频率信息，这部分基本不含EEG信号的信息。因此，在这项研究中，使用D2-D4细节分量和低频分量A4。

2.2 排列熵(PEn)

PEn由Bandt和Pompe[27]提出。PEn用比较相邻值的方式度量时间序列的复杂性。它具有简单、健壮和计算成本极低的优势[28]。给定时间序列(xt,t=1,2,…,T)，相空间重构向量为Xt=[xt,xt+1,…,xt+(n-1)l]，嵌入维数n，延迟时间l(此处l=1)[29]。然后对每个重构分量Xt以升序排列，提取各个分量在原重构向量中的索引，可以得到不同的符号序列。n维相空间映射n!种不同的符号序列。设f(π)为时间序列π出现的概率，其相对概率为p(π)=f(π)/(T-(n-1)l)。排列熵定义为[28]：

(2)

文中按判断每个睡眠状态的30sEEG信号数据计算PEn，当计算90s、150s、210s的参数时，采用滑动窗口提取PEn，将当前睡眠状态的30s前后的时间片加入到参数计算中。

2.3 Petrosian分形维数(PFD)

分形维数是用混沌方法计算信号的复杂性[30]。PFD便于分形维数的快速计算。PFD将信号转化成二进制序列[31]。PFD可以由以下表达式计算：

PFD=log10k/(log10k+log10(k/(k+0.4Nδ)))

(3)

其中，k是信号的样本数；Nδ表示信号符号改变的次数。

PFD与排列熵的计算采用相同的滑动窗获得90s、150s、210s时间片的参数。

2.4 随机森林分类器

Breiman于2001年提出一种新的组合分类算法——随机森林算法(Random Forests,RF)[32]。相比其他优秀的分类方法，如人工神经网络和支持向量机，它揭示了快速计算的优点，精度高、避免过拟合、抗噪能力好。因此，随机森林算法已经广泛应用于生物信息学的分类[33-34]。

随机森林是通过自助法(Bootstrap)的重复采样技术，即从原始训练样本集N中有放回地重复且随机抽取k个样本生成新的训练样本集合，然后根据所抽取的k个样本生成k棵决策树组成随机森林。随机森林的实质是对决策树算法的改进，随机森林中的每一棵决策树都是由分类回归树(CART)算法所构建的未剪枝的决策树。森林中的每棵树的建立依赖一个独立抽取的样本，并且每棵树都具有相同的分布，分类的误差取决于每一棵决策树的分类能力以及它们之间的相关性。

随机森林的生成主要包括以下几个步骤：

(1)采用Bootstrap方法在原始训练样本集N中抽取k个新的训练样本集，一般情况下要求每个新的训练集的样本容量与N一致。

(2)对抽取的k个训练样本集进行学习，并以此生成k个决策树模型。在决策树的生成过程中，假设输入变量一共有M个，从这M个输入变量中随机抽取F个，每个内部节点均是选择这F个特征变量上最优的方式来分裂，且F的值在随机森林模型的形成过程中恒定。

(3)针对分类问题，将k个决策树的分类结果进行组合，形成最终的结果，组合方式是简单多数投票法。

3 实验结果

特征提取所得的各层小波系数的均值与方差(D4-Mean-Std，D4MS)、排列熵、Petrosian分形维数是从不同的角度取得的脑电信号的特征。其中D4MS与脑电信号δ频段(1～4Hz)、θ频段(4～8Hz)、α频段(8～13Hz)、β频段(13～30Hz)具有良好的相关性，而PEn与PFD计算了脑电信号的复杂度，对D4MS中对EEG信号的特征具有补充作用，所以文中选择这三种参数作为睡眠分期的依据。

将特征提取所获得的PFD、D4MS、PEn一共10项特征参数以及人工睡眠状态分类结果作为分类器的输入。采用Weka工具包，并选择其中的随机森林对睡眠状态进行分类。

分类将随机选取每一睡眠状态80%的数据(16 656个样本)作为训练集，剩下的20%(4 158个样本)作为测试集。表2给出了单参数输入时随机森林分类的准确率。

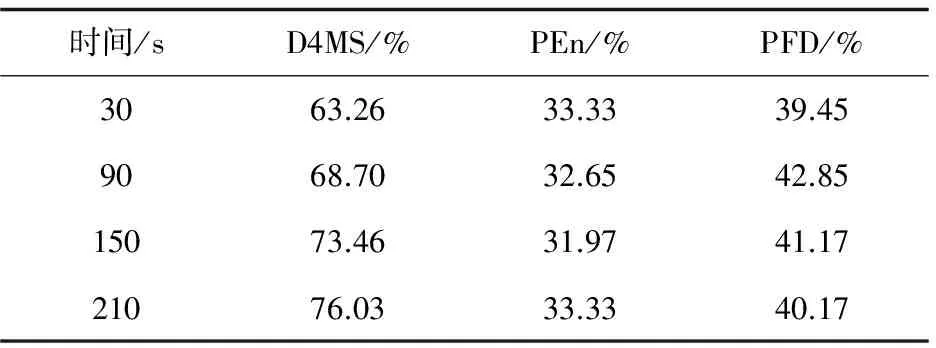
表2 单参数输入分类准确率

由表2可以看出，把对不同时间片提取的PEn作为分类器输入的分类准确率相近，在32%左右，而其他两种参数的分类准确率在不同时间片上差距较大。其中PFD的分类准确率在时间片为90s时达到最高(42.85%)，各层小波系数的均值和标准差在时间片为210s时的分类准确率达到最大(76.03%)。以上结果为10次实验的结果的平均值，是在随机森林节点数为25，且随机森林中每棵决策树都随机选择60%的训练样本作为分类依据时得出。

传统的每30s提取的特征参数D4MS、PEn、PFD作为分类器输入得到的分类结果如图1所示。

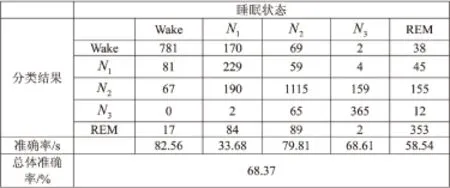
图1 每30 s提取特征参数的分类结果

由图1可见，N1、N3以及REM期的分类准确率较低，其中N1期误判为觉醒期，分类准确率也最低，只有33.68%。

采用单参数输入准确率最高的参数组合作为随机森林输入，各参数输入顺序为D4MS、PEn、PFD，图2是测试样本的自动睡眠分期结果。

图2 优化参数提取的分类结果

比较图1与图2可知，新的参数提取方式可以达到更高的分类准确率，觉醒期的分类结果并无明显变化，其他各睡眠状态的分类准确率都有所提高。其中对N2期的分类达到了91.91%的准确率，N1、N2以及N3期的误判概率都减小了，N1期的分类准确率仍存在很大的提升空间。

图3给出了部分的随机森林分期结果与人工分期结果的比较。

图3 部分分期结果比较

从图中可见，随机森林的分类结果大致与人工分期结果一致，其中REM期与N2期，N2与N3期之间存在的误判相对较多，觉醒期中有小部分误判成N1、N2期，结果基本与图2相符。

4 结束语

文中主要介绍了一种新的睡眠分期特征参数提取方式，在自动睡眠分期中引入了单个睡眠状态判断时期前后的EEG信号对睡眠分期结果的影响。研究结果表明，采用新的方式所提取的特征参数有效提高了自动睡眠分期的准确率。

[1]PanST,KuoCE,ZengJH,etal.AtransitionconstraineddiscretehiddenMarkovmodelforautomaticsleepstaging[J].BioMedicalEngineeringOnLine,2012,11:52-71.

[2] 王小丹,高允锁,郭 敏.大学生睡眠质量及其影响因素的综述[J].中国热带医学,2006,6(10):1906-1907.

[3] 唐向东,李廷利.首次中德睡眠研究学术讨论会综述[J].中国科学基金,2008,22(5):277-281.

[4] 谢松云,张振中,杨金孝,等.脑电信号的若干处理方法研究与评价[J].计算机仿真,2007,24(2):326-330.

[5]FathimaT,BedeeuzzamanM,FarooqO,etal.Waveletbasedfeaturesforepilepticseizuredetection[J].MESJofTechnolandManag,2010,2(1):108-112.

[6]YuenCT,SanWS,RizoniM,etal.ClassificationofhumanemotionsfromEEGsignalsusingstatisticalfeaturesandneuralnetwork[J].InternationalJournalofIntegratedEngineering,2010,1(3):71-79.

[7]AlbayrakM,KoklukayaE.ThedetectionofanepileptiformactivityonEEGsignalsbyusingdataminingprocess[J].e-JournalofNewWorldSci.Acad,2009,4(1):1-12.

[8]SubasiA.EEGsignalclassificationusingwaveletfeatureextractionandamixtureofexpertmodel[J].ExpertSystemswithApplications,2007,32(4):1084-1093.

[9]OzsenS.Classificationofsleepstagesusingclass-dependentsequentialfeatureselectionandartificialneuralnetwork[J].NeuralComputing&Applications,2013,23(5):1239-1250.

[10]GandhiTK,ChakrabortyP,RoyGG,etal.Discreteharmonysearchbasedexpertmodelforepilepticseizuredetectioninelectroencephalography[J].ExpertSystemswithApplications,2012,39(4):4055-4062.

[11]SenB,PekerM.NovelapproachesforautomatedepilepticdiagnosisusingFCBFfeatureselectionandclassificationalgorithms[J].Turk.J.Electr.Eng.Comput.Sci.,2013,21:2092-2109.

[12]MohseniHR,MaghsoudiA,ShamsollahiMB.SeizuredetectioninEEGsignals:acomparisonofdifferentapproaches[C]//Proceedingsofthe28thIEEEEMBSannualinternationalconference.NewYork,USA:IEEE,2006:6724-6727.

[13]AlessandroMD,VachtsevanosG,HinsonA,etal.Ageneticapproachtoselectingtheoptimalfeatureforepilepticseizureprediction[C]//Proceedingsofthe23rdannualinternationalconferenceonengineeringinmedicineandbiologysociety.Istanbul,Turkey:IEEE,2001:1703-1706.

[14]KannathalN,ChooM,AcharyaU,etal.EntropiesfordetectionofepilepsyinEEG[J].ComputMethodsProgBiomed,2005,80:187-194.

[15]SrinivasanV,EswaranC,SriraamN.Artificialneuralnetworkbasedepilepticdetectionusingtimedomainandfrequencydomainfeatures[J].JournalofMedicalSystems,2005,29(6):647-660.

[16]BruzzoAA,GesierichB,SantiM,etal.PermutationentropytodetectvigilancechangesandpreictalstatesfromscalpEEGinepilepticpatients-Apreliminarystudy[J].NeurologicalSciences,2008,29(1):3-9.

[17]GengS,ZhouW,YuanQ,etal.EEGnon-linearfeatureextractionusingcorrelationdimensionandHurstexponent[J].NeurologicalResearch,2011,33(9):908-912.

[18]BaoFS,LieDY,ZhangY.AnewapproachtoautomatedepilepticdiagnosisusingEEGandprobabilisticneuralnetwork[C]//Proceedingsofthe2008 20thIEEEinternationalconferenceontoolswithartificialintelligence.WashingtonDC,USA:IEEE,2008:482-486.

[19]SezerE,IsikH,SaracogluE.EmploymentandcomparisonofdifferentartificialneuralnetworksforepilepsydiagnosisfromEEGsignals[J].JournalofMedicalSystems,2012,36(1):347-362.

[20]SenB,PekerM,ÇavuogluA,etal.AcomparativestudyonclassificationofsleepstagebasedonEEGsignalsusingfeatureselectionandclassificationalgorithms[J].JournalofMedicalSystems,2014,38(3):1-21.

[21]GoldbergerAL,AmaralLA,GlassL,etal.PhysioBank,PhysioToolkit,andPhysioNet:componentsofanewresearchresourceforcomplexphysiologicsignals[J].Circulation,2000,101(23):215-220.

[22]HasilogluA.Rotation-invarianttextureanalysisandclassificationbyartificialneuralnetworksandwavelettransform[J].TurkishJournalofEngineeringandEnvironmentalSciences,2001(5):405-413.

[23] 曹怀信,赵建伟.小波分析发展综述[J].咸阳师范学院学报,2002,17(6):5-8.

[24] 成礼智,王红霞,罗 永.小波的理论与应用[M].北京:科学出版社,2004.

[25]SubasiA.Applicationofadaptiveneuro-fuzzyinferencesystemforepilepticseizuredetectionusingwaveletfeatureextraction[J].ComputersinBiologyandMedicine,2007,37:227-244.

[26]MahajanK,VargantwarMR,RajputMS.ClassificationofEEGusingPCA,ICAandneuralnetwork[J].InternationalJournalofEngineeringandAdvanceTechnology,2011(1):80-83.

[27]BandtC,PompeB.Permutationentropy:anaturalcomplexitymeasurefortimeseries[J].PhysicalReviewLetters,2002,88(17):174102.

[28]LiuXF,WangY.Fine-grainedpermutationentropyasameasureofnaturalcomplexityfortimeseries[J].ChinesePhysB,2009,18(7):2690-2695.

[29] 姚文坡,刘铁兵,戴加飞,等.脑电信号的多尺度排列熵分析[J].物理学报,2014,93(7):419-425.

[30]PetrosianA.KolmogorovcomplexityoffinitesequencesandrecognitionofdifferentpreictalEEGpatterns[C]//Proceedingsofthe26thIEEEinternationalsymposiumoncomputerbasedmedicalsystems.Lubbock,Texas:IEEE,1995:212-217.

[31] 聂笃宪,曾文曲,文有为.分形维数计算方法的研究[J].微机发展(现更名:计算机技术与发展),2004,14(9):17-19.

[32]BreimanL.Randomforests[J].MachineLearning,2001,45(1):5-32.

[33]YuanM,HuXZ.Predictingmembraneproteintypesusingtherandomforestsalgorithm[J].ActaBiophysicaSinica,2009,25(5):349-355.

[34]AlanJ,BogunovicN.Randomforest-basedclassificationofheartratevariabilitysignalsbyusingcombinationsoflinearandnonlinearfeatures[J].IFMBEProceedings,2010,29(1):29-32.

Research on Sleep Staging Method Based on Feature Extraction of EEG

LI Fei,MA Qian-li

(College of Telecommunications & Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

Researches on sleep staging is not only the basis of diagnosing sleep related diseases,but also the precondition of sleep quality evaluation,which has vital significance.A new method to extract EEG features is proposed which effectively improves the accuracy of sleep staging.Different from traditional automatic sleep staging method,sleep stage is classified every 30 seconds and time slice for feature extraction is respectively divided into 30 seconds,90 seconds,150 seconds and 210 seconds to study characteristic parameters of difference time slices on the accuracy of sleep stage.Besides,a random forest classifier in Weka tools is adopted to identify sleep state.The result shows that putting wavelet packet coefficients obtained by the 210 s time slice,the permutation entropy from the 30 s time slice and the Petrosian fractal dimension from 90 s time slice as the parameters of the automatic sleep staging,it can get accuracy of 85%,while three kinds of parameters in 30 s time slice above can only reach accuracy of 65%.

sleep stage;EEG;wavelet packet coefficient;permutation entropy;Petrosian fractal dimension

2016-02-24

2016-06-23

时间：2016-11-22

国家自然科学基金资助项目(61201029)

李 斐(1991-)，女，硕士研究生，研究方向为无线通信与信号处理技术；马千里，副教授，研究生导师，研究方向为嵌入式系统软硬件设计、信号检测与处理、图像处理、生物医学电子学等。

http://www.cnki.net/kcms/detail/61.1450.TP.20161122.1227.030.html

TP301

A

1673-629X(2017)01-0177-05

10.3969/j.issn.1673-629X.2017.01.040