投资者情绪与动态资产定价模型*
2017-02-22华南理工大学经济与贸易学院肖勋勇深圳职业技术学院经济学院张壬癸
华南理工大学经济与贸易学院 肖勋勇 深圳职业技术学院经济学院 张壬癸
投资者情绪与动态资产定价模型*
华南理工大学经济与贸易学院 肖勋勇 深圳职业技术学院经济学院 张壬癸
为了研究易变的投资者情绪对资产价格的影响,本文建立了动态行为资产定价模型。该模型表明在均衡时投资者情绪影响单个情绪投资者的认知价格,而且时变投资者情绪导致了多样的价格变化形式。在多个交易者情况下,投资者情绪影响投资者下期的财富比例,而且股票价格是所有情绪投资者的认知价格的财富比例加权平均值。最后,模型从投资者情绪对财富波动的影响机理出发,阐述了收益长期反转现象,即对价格过度波动异象和收益长期反转之谜给出了部分解释。
投资者情绪 时变情绪 资产定价模型
一、引言
传统的资产定价理论认为,在构建资产定价模型时只需要考虑理性投资者的行为,可以忽略非理性投资者的行为。然而,对于20世纪70年代以来金融市场出现的诸多异象以及投资者的异常行为,传统“理性人”的金融理论难以给出令人满意的解释。行为金融认为噪音、认知偏差、投资者情绪等都会影响投资策略,从而影响资产价格。近期越来越多的实证研究和实验研究都表明投资者心理、投资者情绪和行为对资产价格有重要影响。
在实证研究方面,国外学者Baker和Wurgler(2006),Baker、Wurgler和Yuan(2012),Brown和Cliff(2005)、Lee、Shleifer和Thaler(1991),Kumar和Lee(2006)、Schmeling (2009),Kurov(2010),Liao、Huang和Wu(2011),Stambaugh、Yu和Yuan(2012),Yu和Yuan(2011)以及国内学者王美今和孙建军(2004),伍燕然和韩立岩(2007),谢军、杨春鹏、闫伟(2012)等,都对投资者情绪与股票收益的相关性进行深入研究。Statman et al.(2008)对相关结果给予了金融实验的支持。尽管已有研究结果略有差异,但都认为投资者情绪对股票市场收益有着重要影响。
在理论模型方面,目前对基于投资者情绪的资产定价模型的研究正蓬勃发展,这类研究包括Lawrence、McCake和Prakash(2007)提出的基于情绪的DDM模型,Shu(2010)提出的基于投资者情绪的CCAPM模型,Yang、Xie和Yan (2012)基于投资组合理论建立了情绪资本资产定价模型,以及Yang和Zhang(2013)建立的基于投资者情绪的静态资产定价模型等。例如Shu(2010)在Lucas(1978)的基础上考虑了投资者情绪对风险偏好和贴现因子等的影响。其分析结果表明,股票、债券价格和投资者情绪正相关,预期资产收益与情绪负相关。在情绪高涨时,情绪对资产价格的影响增加。相对于债券市场,情绪变化对股票市场有更大的影响。
目前大部分资产定价模型有一个显著特征:投资者信念没有随着时间的推移而改变。为了研究随着时期的推移投资者情绪如何影响资产价格,本文从投资者情绪视角构建动态行为资产定价模型。在Yan(2010)的模型框架下,本文将投资者情绪引入模型中。与其不同的是,本文假设投资者对未来的红利增长率有其主观的情绪,而不是一个均值为零的噪音。这是因为在牛市(或熊市)时,大部分投资者可能持有较乐观(悲观)的情绪,其均值并不等于零。另外,本文研究了时变情绪对资产价格的影响,模型分析表明时变情绪是导致资产价格波动的重要因素。在多个交易者情况下,投资者情绪影响投资者下期的财富比例,而且股票价格是所有情绪投资者的认知价格的财富比例加权平均值。最后,模型说明了由于投资者情绪导致财富分化,最终导致了收益长期反转现象,即模型对收益长期反转之谜给出了部分解释。
二、动态行为资产定价模型
在基于消费的资产定价模型框架下,考虑一个最简单的两期动态模型,此模型有三个日期t=0,1,2。假设对于t=1,2,消费满足如下过程:

其中,gCt增长率是独立同正态分布(i.i.d.N(μC,σ2C))。资本市场上有两种资产,无风险资产和风险资产(股票)。股票在三个日期都发放正的红利,这些红利满足如下过程:

其中,gDt增长率是独立同正态分布的(i.i.d.N(μD,σ2D))。Campbell(2003)的研究表明消费增长率gCt和红利增长率gDt的相关性为0.05,可近似认为独立。
假设受情绪影响的投资者i对股票红利的平均增长率有乐观或悲观的看法,其主观预期为

其中,SIi和f(SIi)的假定类似于静态模型的假定,即投资者情绪是情绪随机变量S的一个独立抽样值,随机变量S具有均值S和方差σ2SI。函数f是关于投资者情绪的单调递增的函数,并且满足:当投资者持有乐观情绪时(SIi>0),有f (SIi)>0,从而主观的平均增长率大于实际红利(μiD>μD);当投资者持有悲观情绪时(SIi<0),有f(SIi)<0,从而平均的主观红利小于实际红利(μiD<μD);当投资者的主观预期与实际吻合时(SIi=0),有f(SIi)=0,此时平均的主观红利等于实际红利(μiD=μD)。
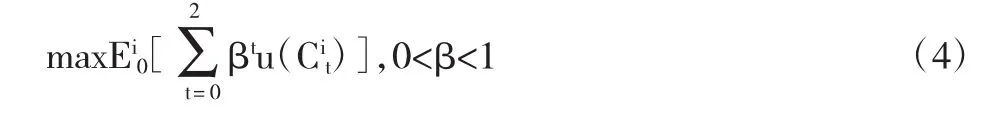
其中,E0表示第0期期望,Cit是投资者i在各期的消费,u是递增、两阶可微的、凹的连续函数,设其具体的形式为对数函数:u(Cit)=1nCit。β是主观贴现因子,它被用来度量消费者推迟消费的忍耐程度。投资者投资于风险资产,其约束条件为:

其中,rSt+1为股票在t+1期的认知收益率。认知收益率满足:
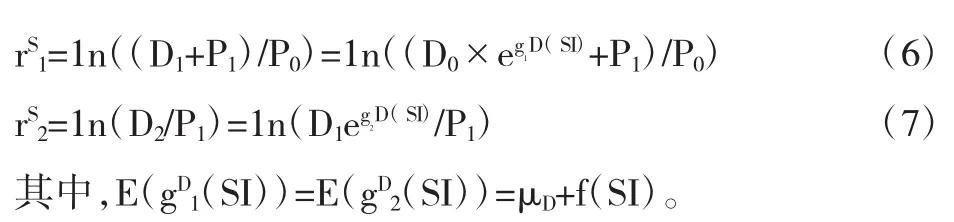
类似于求解传统的欧拉方程的方法,得到如下包含投资者情绪的欧拉方程:

与传统欧拉方程(1=E(β(Ct+1/Ct)-1rt))相比,含有投资者情绪的欧拉方程表明当投资者情绪是乐观时,其认知的主观收益增加,导致当前消费减少;反之,当投资者情绪悲观时,其认知的主观收益减少,导致当前消费增加。
三、模型讨论
(一)代表性投资者
(1)理性投资者。假设在同质的经济环境中,只有一类理性的代表性行为人。根据传统的欧拉方程,可以得到定价方程:
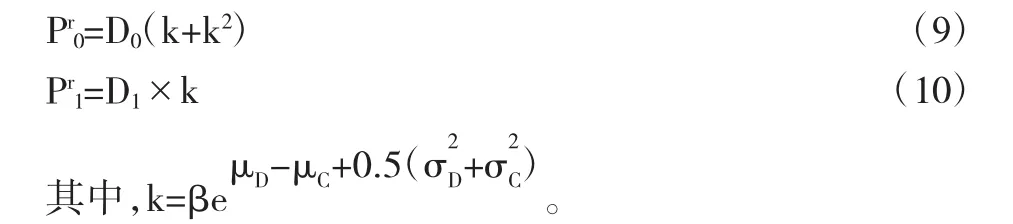
在上述假定之下,投资者i的目标函数为:
对比上述两个公式可知,0期均衡价格由包含红利的两项式子构成,而1期均衡价格由包含红利的一项式子构成。定价公式(9)和(10)的含义是股票均衡价格与未来的股票红利相关。由于在0期拥有两期的股票红利,因此0期股票价格受到两次红利的影响。而在1期未来只有1期股票红利,因此1期价格只受到一次红利的影响。由于0期的两个红利中包含了1期的单个红利,因此一般来说0期均衡价格要大于1期均衡价格。但在牛市中,出现了早期价格低于后期价格(如图1),该现象用传统的定价公式难以解释。Campbell (2003)依据美国市场的数据,估计相关参数如下:μD=2%,μC=2%,σD=15%,σC=2%,从而参数k的估计值为0.9913。牛市中的红利参数设置如下:D0=1,D1=1.8。
(2)情绪投资者。假设在同质的经济环境中,只有一个受自身情绪影响的代表性行为人。类似于求解传统的定价方程,得到如下定价方程:
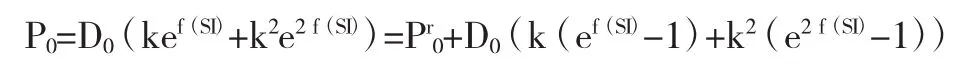

图1 理性价格和市场价格
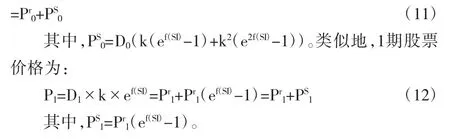
由公式(11)和(12)可知,均衡价格由两部分构成:理性部分和情绪部分。理性部分是理性价格,情绪部分是投资者情绪驱动的情绪价格。当情绪为0时,情绪价格为0,此时定价公式与传统定价公式一致。一般地,乐观投资者情绪导致正的情绪价格,从而放大均衡价格,悲观投资者情绪导致负的情绪价格,从而降低均衡价格。为了从数量上展示情绪价格和理性价格的差异,下面进行数值模拟。假设情绪影响函数为f(SI)=eαSI-1,其中α是大于0的常数。模型参数设置如下:α=0.1,SI∈[-6,6],其他参数和上面数值模拟案例一致。数值模拟如图2所示。该图表明情绪价格随情绪的增加而上涨,当情绪高涨到一定程度时,情绪价格可以超越理性价格。
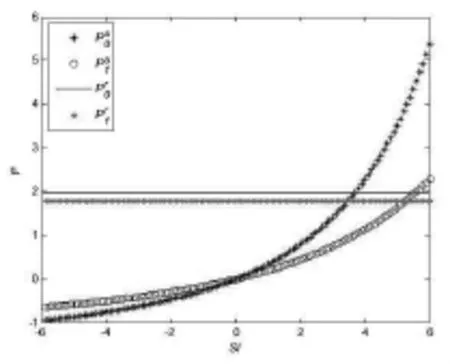
图2 理性价格和情绪价格
对比定价公式(11)和(12)可知,0期均衡价格受到两期情绪影响,由于此时对未来两期的情况均不能确定,因此受情绪的影响较大;而1期均衡价格只受到一期情绪影响,由于只对2期的情况不确定,受到情绪影响相对较小。也就是说随着股票清算日的临近,信息陆续披露,均衡价格越趋于基础价值。
传统观点认为,当均衡价格没有受到投资者情绪影响时,由两部分红利贴现组成的0期价格一般大于只由一部分红利贴现组成的1期价格。但是当均衡价格受到投资者情绪影响时,0期价格可能低于1期价格。其充要条件为f(SI)<ln(D1/D0-1)-ln(k)。为了从数量上展示情绪对均衡价格的影响,在上述数值模拟求出价格变化,模拟结果如图3所示。该图表明均衡价格随着投资者情绪的增加而递增。例如当投资者情绪从-6变化到6的过程中,0期均衡价格从1.03增加到7.34,1期均衡价格从0.66增加到2.37,价格变化(ΔP=P1-P0)从0.14减少到-1.82。当投资者情绪处于区间[-6,2]时,1期均衡价格一直大于0期价格,即投资者情绪增加了股票价格的波动性。因此对于股价高波动性的金融异象,模型给出了一部分解释。
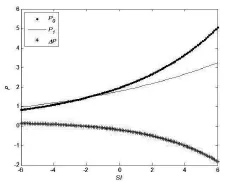
图3 两期均衡价格与投资者情绪
(3)时变情绪。目前大部分资产定价模型有一个显著的特征:投资者信念没有随着时间的推移而改变。该假设过于简单,而且和现实不相吻合。为了研究时变情绪的动态效果,在此放松这个假设。假设在0期投资者情绪SI0与1期投资者情绪不同。类似不变情绪的资产定价公式的推导,则均衡价格满足如下方程:

与公式(14)相比,公式(13)表明0期均衡价格受到情绪组合(SI0,SI1)的影响。情绪组合的变化导致各种价格变化。首先,如果代表性投资者依据更多的信息来更新其情绪,那么投资者的定价错误会随着时间的推移而减少。反之,如果代表性投资者继续维持乐观或悲观的看法,则均衡价格远离理性价格。
其次,如果代表性投资者在两期的情绪是相反的,那么对于0期的均衡价格而言,乐观效果和悲观效果在一定程度上会相互抵消,导致0期的均衡价格较趋近于理性价格,但情绪的综合效果依然影响均衡价格。这是因为综合效果为0的情况要满足极其严格的数量关系。
最后,时变情绪同样导致0期价格小于1期价格,而且相对于不变情绪,价格的波动更大。例如,代表性投资者在0期是悲观情绪,而在1期是乐观情绪,导致0期价格下降幅度增加,而1期价格上升幅度增加,从而有更大的价格变化范围。
为了从数量上展示时变情绪对均衡价格的影响,下面进行数值模拟。模型的函数和参数设置与上述模拟案例一致。数值模拟结果如图4和图5所示。图像说明时变情绪对均衡价格有重大影响。例如当情绪组合为(SI0=6,SI1=0),也就是投资者获取更多信息后,投资者情绪回落到理性情况,此时0期均衡价格为6.08。而不变情绪组合(SI0=SI1=6)导致均衡价格为7.34,因此价格6.08更接近理性价格。通过类似的讨论,也可以说明情绪的抵消效果导致均衡价格更趋近于理性价格。

图4 均衡价格、不变0期情绪与变化1期情绪

图5 均衡价格、变化0期情绪与不变1期情绪
为了从数量上展示时变情绪对价格变化的影响,下面进行数值模拟,其中模型函数和模型参数设置保持一致。数值模拟如图6所示。与不变情绪的图3相比,图6显示时变情绪导致更大的价格变化。例如当情绪SI0=-6时,其对应的价格变化曲线是向上倾斜的,而在图3中对应的曲线是向下倾斜的。

图6 时变情绪与价格变化
(二)两类投资者
(1)理性投资者和情绪投资者。如果在市场上存在两种异质性投资者:理性投资者(r)和情绪投资者(s),假设其初始的财富相同,即Wr0=WS0=0.5。根据Cox和Huang(1989)的方法,市场的完备性意味着动态性约束可以写成静态的形式,最优化问题可以改写为:
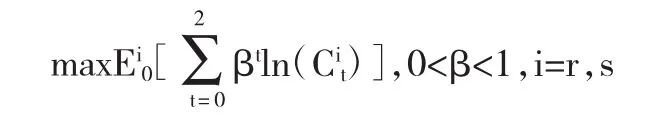
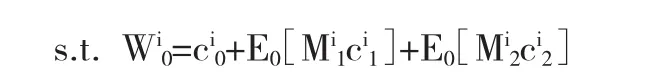
其中,M是随机贴现因子。均衡资产价格满足:

其中,Pi0和Pi1(i=s,r)是只有投资者i时决定的股票价格,参见公式(11)和(12)。权重w满足:

其中理性投资者对应的参数λr=1,而情绪投资者对应的参数λS满足:
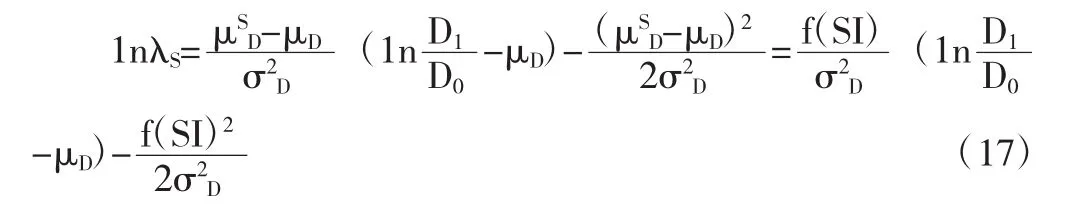
定价公式(15)的经济含义在于均衡价格等于两个异质性投资者的认知价格的加权平均值,权重为投资者的财富比例。也就是拥有更多财富的投资者,其认知价格对均衡价格的影响更大。由代表性投资者的讨论可知,投资者情绪对情绪投资者的认知价格有重要影响。因此,本文得出结论:如果情绪投资者拥有更多财富,那么投资者情绪对均衡价格有重要影响。反之,如果理性投资者拥有更多财富,那么均衡价格会趋向于理性价格。
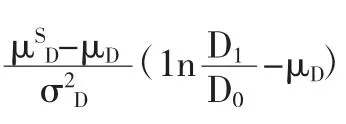
其次,一元二次函数的最大值意味着,当主观预期和实际分红完全一致时,财富比例达到最大,主观预期高估或者低估实际分红,都导致财富比例的减少。即当f(SIi)=1nD1/D0-μD时,财富比例取最大值,也就是主观情绪要与实际分红完全一致,才能取得最大值。即使两者符号相同,从而财富比例有所增加,但如果投资者太乐观或太悲观,导致主观情绪偏离实际分红,都导致财富比例不能达到最大值。总之,如果情绪投资者的主观预期与随机出现的实际情况相吻合,则财富变化加强了情绪对资产价格的影响力,反之,财富变化削弱了情绪的影响力。
为了从数量上展示投资者情绪对1期财富比例的影响,下面进行数值模拟,函数和参数与上例保持一致,数值模拟如图7所示。图7显示当实际红利增加时,即1nD1/D0=0.1,情绪投资者的财富比例向右倾斜,也就是乐观投资者的财富比例增加。当实际红利减少时,即1nD1/D0=-0.1,情绪投资者的财富比例向左倾斜,也就是悲观投资者的财富比例增加。在这两种情况下,当投资者的预期与实际情况完全一致时,财富比例存在一个最大值。

图7 情绪投资者的财富比例
最后,受情绪影响的财富波动可导致收益率可预测。这是因为,如果乐观投资者前期投资更多,当好消息来临时,价格上涨,乐观投资者赚取更多财富。随着财富增加,即在定价公式中价格权重增加,从而乐观投资者继续推高股价。如果在将来出现坏消息,导致以后较低的收益率,反之亦然。这些现象导致了均值反转,也就是1期收益与预期的2期收益之间存在一个负相关关系。这是因为存在投资者情绪时,有:

也就是1期收益与wS1kef(SI)+wr1k正相关,而预期的2期收益与wS1kef(SI)+wr1k负相关,从而cor(r1,E(r2))<0。当没有投资者情绪时,所有投资者可以看成只有一个代表性投资者,那么预期的2期收益是常数,不存在均值反转现象。
对均值反转现象进行数值模拟,参数设置如下:设μD=2%,σD=15%,μC=2%,σC=15%,β=0.98,SI=-3。数值模拟如图8所示。图8表明当不存在投资者情绪时(α=0),2期预期收益是一条平行于横轴(1期收益)的直线,而在投资者情绪影响下,前期收益与未来收益存在负相关的关系,反映了收益率反转现象。动态模型对收益率反转现象给出了一部分解释。
(2)乐观投资者和悲观投资者。如果在市场上存在两种异质性投资者:乐观投资者(o)和情绪投资者(p),他们的情绪满足SIo>0,SIp<0。假设二者初始的财富相同,即wo0=wp0=0.5,此时均衡资产价格满足:

其中,Pi0和Pi1(i=o,p)是只有投资者i时决定的股票价格,参见公式(11)和(12)。权重w满足:
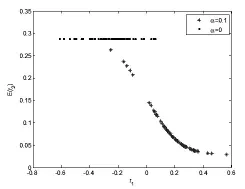
图8 均值反转:理性投资者和情绪投资者
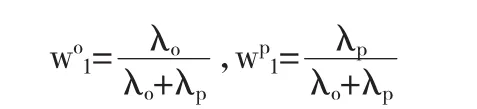
其中,乐观投资者对应的参数λo满足:
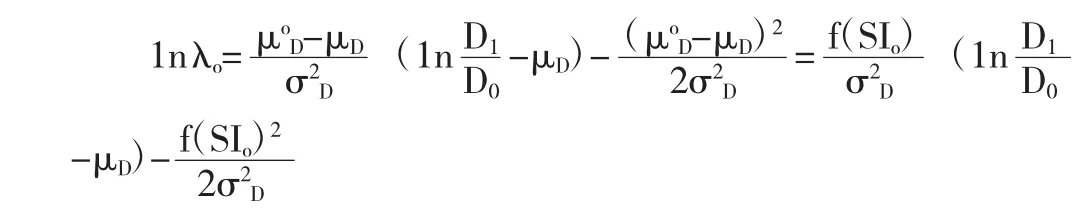
悲观投资者对应的参数λp满足:

类似于对公式(15)的讨论,可知定价公式(18)同样说明投资者情绪对均衡价格和财富比例有重要影响,以及存在均值反转现象。为了从数量上展示投资者情绪对1期财富比例的影响,下面进行数值模拟,SIp∈[-6,0),SIo=2,其他函数和参数与上例保持一致,数值模拟如图9所示。图形显示当实际红利增加时,即1nD1/D0=0.1,悲观投资者的财富比例曲线在红利减少时对应的财富比例曲线下方。也就是当实际红利增加时悲观观投资者的财富比例减少,当实际红利减少时,即1nD1/D0=-0.05,悲观投资者的财富比例增加。当实际红利增加时,乐观投资者的预期可以与实际情况完全一致,此时该乐观投资者的财富比例存在一个最大值;反之当实际红利减少时,悲观投资者的预期可以与实际情况完全一致,此时其财富比例存在一个最大值。

图9 悲观投资者的财富比例
对均值反转现象进行数值模拟,参数设置如下:β=0.98,SIo=3,SIp=-3,其他参数保持一致。数值模拟如图10所示。图10表明当不存在投资者情绪时(α=0),2期预期收益是一条平行于横轴(1期收益)的直线,而在投资者情绪影响下,前期收益与未来收益存在负相关的关系,反映了收益率反转现象。

图10 均值反转:悲观投资者和乐观投资者
与公式(15)不同的是,乐观情绪导致的价格上涨部分会与悲观情绪导致的价格下跌部分在一定程度上相互抵消。在特殊情况下,甚至可以完全抵消,此时均衡价格等于理性价格。由于这种完全抵消的情况对数量有严格的要求,因此在实际中几乎不存在。对此相互抵消的现象进行数值模拟,参数保持一致。数值模拟如图11和图12所示。图11显示当悲观情绪过于悲观时,悲观投资者财富比例过小,因此资产价格主要由乐观情绪投资者主宰。此时更加乐观情绪导致更高的价格,因此乐观情绪值为2的价格曲线在乐观情绪值为4对应的价格曲线下面。当悲观投资者开始向理性趋近时,其财富比例逐渐增加,导致其对未来价格的影响越来越大,此时产生乐观情绪和悲观情绪的相互抵消效应,从而均衡价格逐渐减少。图12显示当乐观情绪与股票实际表现接近时,均衡价格受到乐观情绪的影响而上升;当乐观情绪离股票实际表现相差太大时(见图形的左右两端),产生乐观情绪与悲观情绪的抵消效应,均衡价格下降。
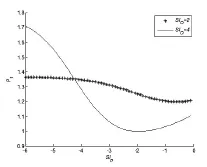
图11 抵消效应:悲观情绪

图12 抵消效应:乐观情绪
(三)N个投资者假定市场上存在N类投资者,对于t=0和t=1,定价公式如下所示:

其中,Pit是只有第i个投资者的股票价格,参见公式(11)和(12)。ωit是第i个投资者的权重,λi与情绪指标有关,即权重与情绪有关。其中
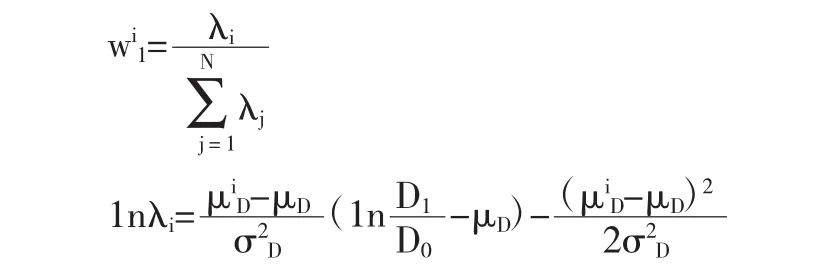
类似于对公式(15)的讨论,可知股票价格是所有情绪投资者的认知价格的财富比例加权平均值。投资者情绪不但影响单个情绪投资者的认知价格,而且在多个交易者情况下影响投资者下期的财富比例。为了从数量上展示投资者情绪对1期财富比例的影响,下面进行数值模拟。模型的函数和参数设置和上例保持一致,数值模拟如图13所示。图形显示当实际红利增加时,即1nD1/D0=0.1,情绪投资者的财富比例向右倾斜,也就是乐观投资者的财富比例增加。当实际红利减少时,即1nD1/D0=-0.1,情绪投资者的财富比例向左倾斜,也就是悲观投资者的财富比例增加。在这两种情况下,当投资者的预期与实际情况完全一致时,财富比例都存在一个最大值。

图13 财富比例与投资者情绪
财富波动导致收益率可预测。乐观投资者前期投资更多,当好消息来临,价格上涨,赚取更多财富,乐观投资者继续推高股价(财富增加,从而价格权重增加),导致以后较低的收益率;反之亦然。这些现象导致了均值反转,也就是1期收益与预期的2期收益之间存在一个负相关关系。这是因为存在投资者情绪时,有:
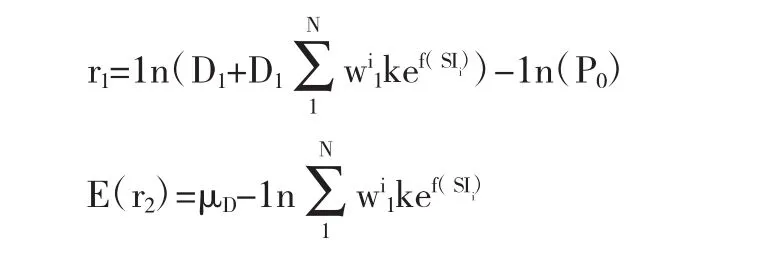
当没有投资者情绪时,所有投资者可以看成只有一个投资者,那么:

也就是预期的2期收益是常数,不存在均值反转现象。
对均值反转现象进行数值模拟,N=121,其他参数保持一致。数值模拟分成三组,第一组假设众多投资者的投资者情绪在区间[-6,6]中的分布是对称的,即SIi=-SIN+1-i;第二组假设投资者情绪在区间[-1,6]中服从均匀分布,即绝大多数投资者情绪是乐观的;第三组假设投资者情绪在区间[-6,1]中服从均匀分布,即绝大多数投资者情绪是悲观的。数值模拟如图14、15和16所示。这些图形都表明当不存在投资者情绪时(α=0),2期预期收益是一条平行于横轴(1期收益)的直线,而在投资者情绪影响下,前期收益与未来收益存在负相关的关系,反映了收益率反转现象。动态模型对收益率反转现象给出了一部分解释。
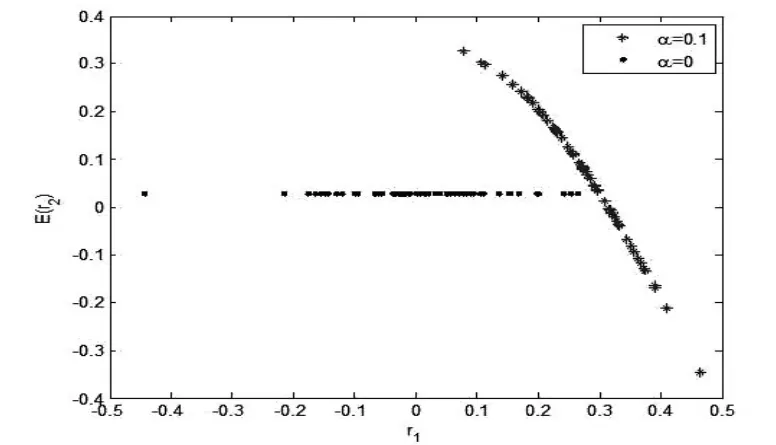
图14 对称投资者情绪与均值反转
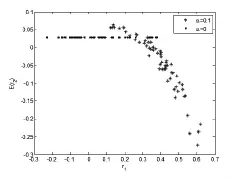
图15 乐观情绪与均值反转
四、结论
本文基于投资者情绪建立了动态资产定价模型,并给出数值模拟结果。在考虑代表性投资者的情况下,动态模型显示均衡价格由理性部分和情绪部分组成,投资者情绪导致了资产价格的多样性。与传统的前期价格大于后期价格的观点不同,由于悲观情绪的影响,可能导致前期资产均衡价格小于后期均衡价格。另外,时变情绪的波动增加均衡价格的波动性。
在考虑异质性投资者的情况下,动态模型显示均衡资产价格是所有情绪投资者的认知价格的财富比例加权平均值。投资者情绪不但影响单个情绪投资者的认知价格,而且在多个交易者情况下影响投资者下期的财富比例。财富的波动导致了收益均值反转现象,动态模型对均值反转异象给出了一部分解释。与传统自然选择观点不同,具有理性投资者和情绪投资者的动态模型显示当情绪投资者的预期与股票实际表现更接近时,情绪投资者的未来财富超过了理性投资者,即情绪投资者并不会被理性投资者所清除。另外,具有乐观投资者和悲观投资者的动态模型显示乐观情绪的影响会被悲观情绪部分抵消,但是其剩余的部分在一般情况下并不等于零,仍然对资产价格有影响。
*本文系广东省哲学社会科学“十二五”规划学科共建项目(项目编号:GD15XLJ03)、教育部高等学校博士学科点专项科研基金项目(项目编号:20120171110040)阶段性研究成果。
[1]王美今、孙建军:《中国股市收益、收益波动与投资者情绪》,《经济研究》2004年第10期。
[2]伍燕然、韩立岩:《不完全理性、投资者情绪与封闭式基金之谜》,《经济研究》2007年第3期。
[3]谢军、杨春鹏、闫伟:《高频环境下股指期货市场情绪冲击效应研究》,《系统工程》2012年第9期。
[4]BakerM,WurglerJ.InvestorSentiment,the Cross-section of Stock Returns[J].Journal of Finance,2006,61(4)∶164B-1680.
[5]BakerM,WurglerJ,YuanY.Global,Localand Contagious Investor Sentiment.Journal of Financial Economics,2012,104∶272-287.
[6]Brown G,Cliff M.Investor Sentiment,Asset Valuation [J].Journal of Business,2005,78(2)∶40B-440.
[7]Lee C,Shleifer A,Thaler R.Investor Sentiment,the Closed-end Fund Puzzle[J].Journal of Finance,1991,46(1)∶7B-109.
(编辑 朱珊珊)
