股指期货保证金调整对套期保值影响研究
2017-02-22西安邮电大学经济与管理学院郭建峰翟恒超胡滋颖西安邮电大学计算机学院李玉
西安邮电大学经济与管理学院 郭建峰 翟恒超 胡滋颖 西安邮电大学计算机学院 李玉
股指期货保证金调整对套期保值影响研究
西安邮电大学经济与管理学院 郭建峰 翟恒超 胡滋颖 西安邮电大学计算机学院 李玉
本文以2013年8月30至2016年1月31日(共计629日)的沪深300股指期货与沪深300指数的数据为样本,主要利用Copula-GARCH模型来估计股指期货套期保值效率,结合保证金的调整方向,研究在沪深300股指期货交易保证金改变的情况下,不同保证金水平对沪深300股指期货套期保值的影响。
股指期货新规 期现市场 Copula-GARCH 套期保值
一、引言
沪深300指数自推出以来,中国金融期货交易所通过不断调整保证金水平来管理市场风险,调控指数平稳运行。保证金制度作为股指期货交易系统中的重要组成部分,制约市场中的违约风险,维护交易中的信用问题,因此中国金融期货交易所在市场波动加大、整个金融市场面临风险剧烈增加的情况下,通过改变保证金水平等手段抑制市场风险,以期抑制市场投机活动,稳定股指期货市场。但在实际运行过程中,不同的交易保证金水平影响了资金使用效率,更是决定了市场容量,交易保证金的高低直接决定投资者成本,对套期保值效率有突出影响。其中2015年9 月7日保证金水平从10%调升至20%,当日股指期货主力合约价格暴涨130.4点,次日股指期货主力合约更是暴涨了241.8;当日股指期货价指数暴跌115.34点,由此可以观之,调整保证金对沪深300股指期货价格和相关指数水平都会产生显著影响。股指期货套期保值作为连接股票市场和期货市场的有效工具,研究保证金对于股票套期保值效果进行分析可以更深入理解股指期货市场,帮助期货交易所更好地完善规则,为众多金融机构在选择套期保值时提供必要参考,同时拓展套期保值理论。
二、文献综述
随着金融和商品期货等金融衍生产品不断出现,股指期货为市场提供了一个避险渠道,股票投资组合持有人可以通过潜在风险转移,支付风险溢价去寻找愿意承担风险的投资者,然而这样对冲,其策略有效性在很大程度上依赖于保值率估计精度,于是确定最优套期保值效果已经成为风险领域的一个重要课题。进行最优套期保值比率计算上有许多方法,在早期研究中主要有普通最小二乘法(OLS)等静态估算方法,随着研究深入发现采用二元条件波动模型(GARCH)估计随时间变化的套期保值比率可以减少投资组合风险,尤其是将数学函数(Copula)与模型(GARCH)相结合后进行套期保值研究,更进一步证实了动态套期保值效果更优。
Engle(1982)提出动态自回归条件异方差(ARCH)模型框架,该模型考虑现货和期货价格的时间因素,消除了模型回归中序列的异方差性。Bollerslev(1986)在Engle研究的基础上对ARCH模型进行改进,提出时间变化波动率结构的GARCH模型,解决了ARCH模型滞后期过长的缺陷。之后学者们将数学函数与模型相结合进行套期保值研究,Copula函数与GARCH模型的结合的相关理论与方法得到迅速发展。Patton(2006)扩展了标准Copula函数的概念,使用Copula-GARCH模型联合条件密度函数,为现货和期货收益指定边缘条件密度,指定TGARCH模型具有可能不同的参数和误差分布。Hsu、Tseng和Wang(2008)认为动态Copula-GARCH模型估计的最优套期保值比率效果较传统的静态模型和其他GARCH模型更优。Beare(2011)实证了Copula-GARCH模型更适用于套期保值比率的确定研究。Silvo Dajcman(2014)利用Copula-GARCH模型分析两个市场之间的关系。Yih-Wenn Laih(2014)研究了Copula-GARCH模型中金融数据相关关系。Acatrinei(2015)实证检验了Copula-GARCH模型在风险管理中的应用。我国学者对股指期货套期保值比率的研究开始于沪深300推出之后,研究方法大多借鉴国外研究比较成熟的模型,并在此基础上加以改进和创新。张高励(2011)的研究结果显示Copula-GARCH模型确定的套期保值比率优于传统套保模型。俞维思(2012)研究Copula-GARCH模型的套期保值效果,同样得出了最优的套期保值效果。张强(2014)用DCCGARCH模型研究发现,沪深300股指期货与大盘股有高度的相关性。王继莹(2014)也认为Copula-GARCH模型是套期保值策略中最优的。
Derming L等(2013)系统分析保证金的设置水平对金融衍生品的影响。王宣承等(2014)研究在股指期货市场保证金水平偏高的情况下,空头和多头头寸面临不同价格波动的风险状况。庞素琳等(2014)研究沪深300股指期货保证金水平的设置及违约率的确定问题。
三、研究设计
(一)套期保值模型构建最优套期保值比率是指对于一份现货组合合约,需要购买多少数量的期货合约来进行套期保值,该比率可以最小化对冲投资组合风险。传统套期保值理论中假设基差不存在,商品交易者可以通过套期保值完全规避市场风险,其套期保值比率为1;但由于影响同一标的资产因素不一致,造成在某一特定时间点上现货价格与期货价格不相同,产生价格差异(基差),基差的存在使套期保值不能完全规避市场系统性风险,因此需要通过确定最优套期保值比率来获得最大收益或者最小损失。根据这一理论,对股指期货最优套期保值比率的研究可以分为两个方面:从效用最大化角度,研究均值—方差套期保值比率;基于组合收益风险最小化角度,研究最优套期保值比率。由于在实际运算过程中很难针对各类投资组合构造出一个合适的效用函数,故本文在研究股指期货最优套期保值比率时,从组合收益风险最小化角度构建模型。
(1)套期保值模型。假设RP、RS、RF分别为套期保值组合、现货头寸和期货头寸收益率,H为套期保值比率,则:
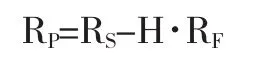
投资组合收益变化方差均值为:
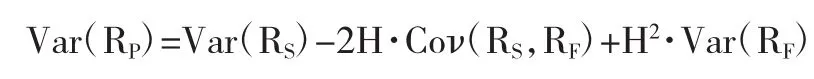
要求Var(RP)达到最小,为此对Var(RP)关于H求一阶导数,得:

由上述关于H的自回归异方差模型(GARCH)可以计算出最优套期保值比率,其通过对期货和现货不同的价格波动进行选择,进而依靠期货组合之间收益弥补现货组合损失,最终使得套期保值组合之间收益率波动最小。
(2)Copula-GARCH模型。本文将GARCH模型和Copula理论相结合得到Copula-GARCH模型,用该模型估计期货和现货之间关系,计算最优套期保值比率。假设现货收益率RS和期货收益率RF的联合分布函数为FS,F(x,y),各自边缘分布为FS(x)和FF(y)。根据copula理论,存在二元copula函数C(u,v)使FS,F(x,y)=C(FS(x),FF(y))。Copula运用联合分布函数将RS和RF的边缘分布组合在一起,准确反应了变量RS和RF之间的相关关系,同时可以由Copula函数推导得出相关系数ρS,F,λU和λV分别为上尾及下尾相关数。同时Copula-GARCH模型在运用的过程中,需要对变量的全局相关性进行度量,所以在典型的金融资产研究结果中要更多地考虑极端事件发生时,一个金融市场的变化对另一个金融市场趋势的影响,即二者尾部相关性的度量。为更好地描述沪深300指数和股指期货的相关性,在构建模型中利用了上尾与下尾的相依对称性,所以利用了函数尾部具有对称性且上下尾相关系数均为0。

σS和σF分别为现货和期货收益率序列的动态标准差,此时基于Copula-GARCH最小方差套期保值模型的最优套期保值比率为:
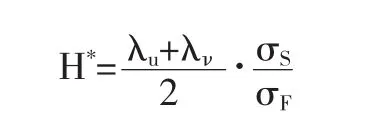
(3)套期保值比率的评价。投资者市场行为的目的是效益最大化和风险最小化,本文将运用风险最小化来分析评价套期保值效果。套期保值前后风险降低的程度用HE指标来衡量,△S表示套期保值前的现货价格收益率;H表示套期保值组合价格收益率的线性组合。套期保值绩效的指标表示如下:
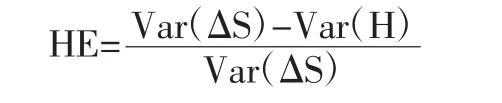
(二)事件分析法
(1)确定事件窗口期。为考察保证金水平对套期保值效率的影响,本文运用事件研究法对该影响进行研究。事件研究法就是通过套期保值效率进行定义,然后确定事件发生的窗口期,在确定的时间段内研究不同保证金水平下套期保值地效率。结合保证金调整方案,本文将保证金调整分为调降和调升两个事件,其中调升事件为在2014年9 月1日将期货保证金从15%调整到10%,调降事件为2015年9 月7日将期货保证金从10%调整到20%。于是本文选定保证金调整前的日期为事件日(时窗0),然后向前和向后分别追溯十个交易日期作为事件时间窗口,共计20个交易日(-10,10),为更全面分析,本文分别采用(-1,1)、(-3,3)、(-5,5)、(-30,30)时间窗口期进行分析。同时为更好衡量事件窗口期的套期保值效率情况,需要对事件向前追溯90个交易日研究在保证金水平稳定情况下的市场状况,因此选取(-90,-30)和(30,90)研究长期套期保值效率。
(2)选取时间数据。金融数据具有尖峰肥尾的特性,更为接近事件发生的交易数据,蕴含更多事件信息,可以更好地考察事件对市场产生的真实影响。为此选取沪深300指数日收盘价为样本数据;同样分别选取沪深300股指期货中交易量占绝大多数的当月股指期货IF00日收盘价为样本数据。本文数据主要通过wind资讯金融终端获得,采用EViews和matlab进行相关性检验和回归建模。
四、实证结果与分析
(一)数据描述性统计首先,使用EViews对数据中的日收益率走势图进行分析,以沪深300股指(CSI300)和沪深300股指期货(IF00)日收益率作为两个基本序列进行描述。股指和股指期货日收益率的偏度均接近于0,峰度大于于3(平峰),与正态分布(S=0,K=3)形态差别比较大。从JB检验来看,沪深300股指和股指期货的伴随概率P值小于0.5,表明不拒绝零假设,不服从正态分布。传统金融市场数据分布呈现尖峰厚尾状态。数据描述性统计见表1。
同时以时间作为横坐标,用RS和RF分别表示沪深300指数和股指期货日收益率,建立坐标图,图1和图2分别为期货保证金调降和调升前后市场日收益率图。从图中可以看出,沪深300股指与股指期货日收益率走势基本一致。

表1 数据描述性统计表

图1 期货保证金调降前后市场日收益率

图2 期货保证金调升前后市场日收益率
(二)套期保值比率确定及评价用matlab软件求得基于原数据的沪深指数与股指期货在各个时间段的相关数据见表2。由表2可以得出如下结论:
(1)在保证金调整前后较短的时间内,股票市场和股指期货市场的Kendall相关系数处于一个相对较低的水平,其正向相依系数非常低说明由于保证金的调整,导致市场非正向相关大幅度波动情况,并且造成股票市场和股指期货市场的运行的偏离,尤其保证金调升对于市场的影响更是非常显著。随着时间的增加,沪深300股指和期指Kendall相关系数也不断调升到一个稳定的关系,这说明沪深300股指和期指收益率之间存在非常显著的同方向的相依关系,并且随时间增加,金融市场自身的调整清洁功能也会发挥作用,使市场处于一个相对稳定状态。
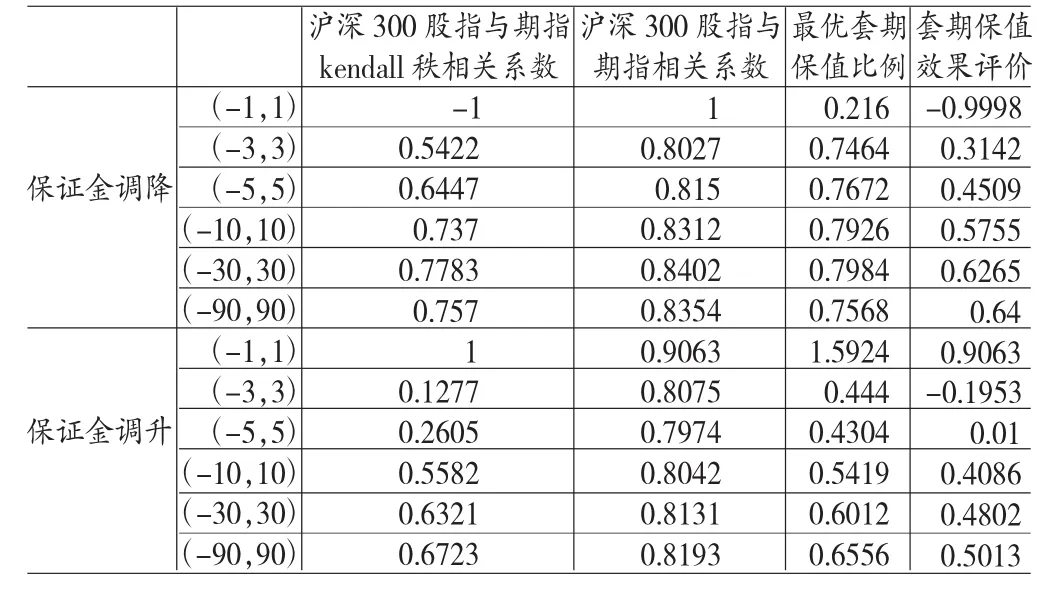
表2 沪深300股指期货与期指收益率套期保值
(2)沪深300股指与期指相关系数非常高,由于沪深300期货指数是以沪深300股指为基础开发出来的指数,其交割价格由股指作为确定标准,这也意味着沪深300期货指数会围绕沪深300指数不断上下波动,很明显二者相关度非常高,基本维持在0.8以上。
(3)由于事件影响,最优套期保值比例在短期的市场走势不明确、风险程度非常高。最优套期保值比率一般应维持在相对较低水平,以免市场出现与预期不相符的走势而增加套期保值损失。调降保证金对于最优套期保值的影响在短期较大,在中期和长期基本处于一个相对稳定状态,其影响非常小;调升保证金在短期和中期影响都非常大,在长期都会存在影响,其最优套期保值比例在短期处于非常低的水平,并且会随着时间增加不断提高。
(4)通过对短期内套期保值效果的评价,可以很清晰看到套期保值效果不好,在保证金进行调整的时间段内要慎用套期保值工具,因为保证金调整对于套期保值影响非常大,套期保值效果会变得非常差。在中长期套期保值效果相对比较稳定,保证金调降在长期内对套期保值效果是一个积极提升的过程,在此时套期保值会真正起到套期保值效果,实现期货作为避险工具的作用;保证金调升后套期保值在长期也会变得相对稳定,套期保值效果一样可以部分实现,但对于整个市场来说会稍有削弱。
五、结论
市场监管者通过对保证金比例进行调整、控制市场交易风险,是进行市场管理的重要举措;套期保值交易者通过股指期货市场进行套期保值,规避系统性风险,实现风险转移,完成金融市场稳定与调节的功能。本文定量研究了期货保证金比例调整对通过Copula-GARCH模型找出收益序列数据分布状况,并对该收益率序列数据进行检验,对保证金调整前后市场状况进行分析,计算出最优套期保值比率,并对套期保值效果进行评价,从而分析出保证金对股指期货市场进行套期保值的影响。所得主要结论如下:
第一,中国金融期货交易所于2014年9月1日下调保证金比例的举措,给市场释放积极、稳定信号,使整个期货市场变得更加活跃,增加了市场的流动性,对于股指期货价格套期保值来说,有效了提高套期保值效率,更大程度上发挥股指期货市场避险功能,因此在市场稳定阶段采取降低保证金的举措更加有利于股指期货市场各项功能的发挥,整个市场会变得更加繁荣。
第二,中国金融期货交易所于2015年9月7日上调保证金比例的举措,降低了市场流动性,增加了交易成本,在中短期抑制了市场投资,降低了套期保值效果,事实上伤害了股指期货交易市场,在长期虽然稳定了套期保值效果,但是实质上仍未恢复到上调前的水平。为此监管部门需要慎用上调保证金这一政策工具,因为上调保证金会损害到整个市场,更要注意短期影响,因为短期内几乎抑制了整个市场套期保值等功能的发挥。
第三,大幅度上调保证金将会对整个市场产生深远影响,其联动作用甚至可以让整个股票市场上演千股涨停、千股跌停的罕见局面,将股指期货套期保值这一作用发挥到相当高的水平,或者让其基本失去效果。在未来出台调整保证金政策时需更加谨慎,在充分预见市场方向的前提下,经过反复论证才可以最终确定新的标准。
[1]王宣承、陈艳:《典型事实约束下的沪深300股指期货动态保证金设定研究》,《投资研究》2014年第1期。
[2]庞素琳、吴曼琪:《股指期货保证金水平设置比较研究》,《管理科学学报》2014年第6期。
[3]俞维思:《基于Copula-ECM-GARCH的沪深300股指期货套期保值比率研究》,《经济研究》2012年第9期。
[4]张强、杨华青:《基于时变Copula的股指期货与金融市场相关性研究》,《东南学术》2014年第4期。
[5]王继莹、郑耀威:《沪深300股指期货套期保值效率度量研究———基于沪深300ETF的实证分析》,《成都理工大学学报:社会科学版》2014年第6期。
[6]T.Bollerslev.GeneralizedAutoregressiveConditional Heteroscedasticity,Journal of Econometrics.1986,(31).
[7]A.J.Patton.Modelling Asymmetric Exchange Rate Dependence,International Economic Review.2006,(47).
[8]Beare.Thehe dging performance of Copula-GARCH[J]. Journal of applied Econometrics,2011(8)∶12-17.
(编辑 朱珊珊)
