基于果蝇算法优化广义回归神经网络的机枪枪管初速衰减建模与预测

曹岩枫，徐诚

(南京理工大学 机械工程学院，江苏 南京 210094)

基于果蝇算法优化广义回归神经网络的机枪枪管初速衰减建模与预测

曹岩枫，徐诚

(南京理工大学 机械工程学院，江苏 南京 210094)

机枪枪管初速衰减预测是一个复杂的非线性问题。广义回归神经网络方法被广泛应用于非线性问题的建模，但其平滑因子取值对神经网络的预测性能有较大影响。采用果蝇算法对广义回归神经网络的参数进行优化选取，提出了基于果蝇算法优化广义回归神经网络的机枪枪管初速衰减建模方法。基于机枪枪管初速衰减试验数据，建立在不同使用环境下随着累计射弹量的增加，以初速降为特征量的机枪枪管初速衰减预测模型，预测结果与试验结果基本一致，证实了所提方法的可行性。通过与未经优化的广义回归神经网络方法和反向传播神经网络方法建立的预测模型进行比较，其性能明显优于另外两种方法，验证了基于果蝇算法优化的广义回归神经网络方法在建立机枪枪管初速衰减模型中的有效性。

兵器科学与技术；果蝇算法；广义回归神经网络；初速衰减；预测模型

0 引言

研究不同使用环境下机枪枪管初速衰减规律，建立初速衰减预测模型，对于确定和评定枪管的使用寿命至关重要。近年来，许多学者对这类非线性问题的预测方法进行了深入研究，杨明华等[1]、张玲等[2]建立了3种大口径机枪加速寿命试验的参数模型，通过统计分析比较后得出了较优的模型；陈国利等[3]提出了采用反向传播(BP)神经网络的方法来计算退化数据, 并根据计算得到的失效阈值进行身管寿命预测；张军等[4]与单永海等[5]研究了身管寿终射弹量与环境应力间的关系，建立了基于最小二乘支持向量机的机枪加速寿命模型。方峻等[6]提出了一种将退化过程的理论模拟与性能退化的实测数据结合起来的分析方法来预测身管的寿命。但对不同使用环境下枪管初速衰减情况的预测分析还鲜有研究。

广义回归神经网络(GRNN)是由Specht等[7]在1991年提出的一种有导师学习神经网络，其主要优点在于它拥有很强的非线性映射能力、高度的容错性和鲁棒性，具有学习速度快、结构简单、对非线性模型的拟合及预测能力较强的特点。由于GRNN的平滑因子取值对神经网络的预测性能有较大影响[8-9]，因此本文采用果蝇算法对GRNN的参数进行优化选取[10-13]，再通过优化后的神经网络模型进行机枪枪管初速衰减预测。

本文采用实际试验数据对预测结果进行验证，并与未经优化的GRNN、BP神经网络模型(BPNN)进行对比，验证了基于果蝇算法优化的广义回归神经网络(FOAGRNN)方法在建立机枪枪管性能衰退模型中的有效性。

1 机枪枪管初速衰减建模

1.1 机枪枪管初速衰减试验数据分析

对于大口径机枪枪管，一般用初速下降量(初速降为初始速度的15%)作为主要寿终标准，通过建立初速衰减模型，可以对不同使用环境下的枪管寿命进行预测。

通过对枪管寿终机理的研究以及对大量试验结果的统计分析表明，试验环境温度、机枪枪管内膛温度、膛压与射击间隔时间等因素都对机枪枪管初速的衰减有着显著地影响。然而，机枪枪管的内膛温度与膛压是其他因素共同作用的结果，不是可以直接控制的应力。因此，选取试验环境温度与射击间隔为试验应力，建立随着累计射弹量的增加，以初速降为特征量的机枪枪管初速衰减模型。

表1为某机枪4根枪管在不同试验环境温度与射击间隔条件下，累计射弹量与其对应的初速值表。其中，试验环境温度分别为常温22 ℃、低温-45 ℃与高温50 ℃，射击间隔时间分别为0.5 min、2.0 min与3.0 min. 由于初速值具有一定的随机性，为了方便比较分析，将每组试验中的初速值分别与其理论初速相比进行归一化处理。

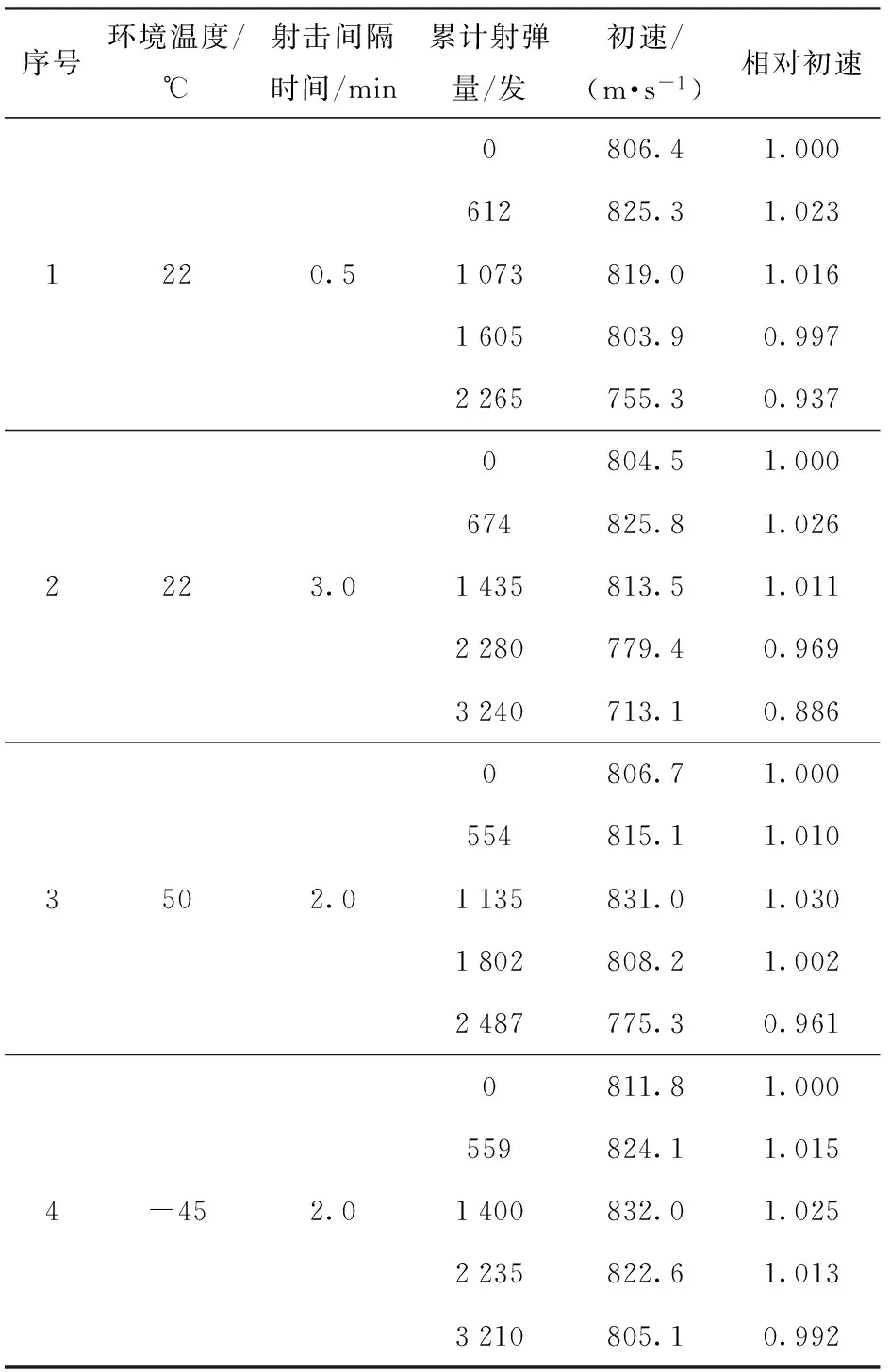
表1 不同使用环境下初速与射弹量对应关系(训练样本)Tab.1 Relationship between muzzle velocity and shooting projectile quantity under various service conditions(training sample)

由表1可以看出，不同环境温度与射击间隔的情况下，随着射弹量的增加，初速均呈现出先上升后下降的衰减趋势，表明枪管初速衰减模型的建立是一个复杂的多元非线性回归问题，因此采用GRNN方法建立初速衰减模型。

1.2 基于GRNN方法的初速衰减建模

GRNN是径向基函数(RBF)神经网络的一个分支，是一种有导师学习神经网络。GRNN在逼近能力和学习速度上比一般的RBF神经网络有更强的优势，能够快速学习并收敛于样本量积聚最多的优化回归面，并且在样本量较小时，预测效果仍然较好。

GRNN的理论基础是非线性回归分析，预测结果为

(1)

式中：X为r维输入变量，X=[x1,x2,…,xr]T；Y为k维输出变量，Y=[y1,y2,…,yk]T，输出GRNN模型的预测结果；f(X,Y)为X和Y的联合概率密度函数；E[Y|X]为给定输入变量X，输出变量Y的期望值。

GRNN的结构如图1所示，由4层构成，分别为输入层、模式层、求和层与输出层。

图1 GRNN结构图Fig.1 Schematic diagram of GRNN architecture

1)输入层。输入层神经元的数目等于学习样本中输入变量的维数r，各神经元接收输入变量并直接传递给模式层。

2)模式层。模式层神经元数目与样本数量n相等，各神经元的传递函数为

(2)

式中：Xi为第i个神经元对应的学习样本；σ为平滑因子。

3)求和层。求和层使用两类神经元进行求和。其中一类神经元对所有模式层神经元的输出进行算术求和，传递函数为

(3)

另一类神经元对所有模式层神经元的输出进行加权求和，模式层中第i个神经元与求和层中第j个神经元的连接权值为输出样本Yi中的第j个元素，传递函数为

(4)

式中：k为输出向量的维数。

4)输出层。输出层的神经元数目等于学习样本中输出向量的维数k，第j个神经元的输出结果对应预测结果的第j个元素，即

(5)

本文的研究中，X为由环境温度、射击间隔与累计射弹量组成的三维向量，Y为相对初速，训练样本数n为20. 通过(2)式～(5)式计算出初速降的预测值。

1.3 基于FOAGRNN的初速衰减预测方法

由上文可以看出，GRNN的训练不需要迭代，隐含层神经元数目与各层之间的连接权重由训练样本唯一确定，平滑因子σ的取值直接影响到神经网络的预测性能。因此，训练网络的过程就是在寻找最佳的平滑因子σ. 为了提高模型的预测精度，采用果蝇优化算法[14]，以平滑因子σ为味道浓度判定值Si，以网络预测值与实际值的均方差(RMSE)为味道浓度判定函数(适应度函数)，动态调整平滑因子σ的取值来优化GRNN模型。

具体步骤(见图2)如下：

1) 确定种群个体数量Nsp与最大迭代次数gmax，并随机确定果蝇群体初始位置(U0,V0)，并令g=0.

2) 赋予果蝇个体利用嗅觉搜寻食物之随机方向Rr与种群半径h.

Ui=U0+2h(Rr-0.5)，

(6)

Vi=V0+2h(Rr-0.5)，

(7)

式中：Rr为[0,1]的随机值。

3) 计算果蝇个体与原点之间的距离Di，并计算味道浓度判定值Si为

(8)

Si=1/Di.

(9)

4) 将各果蝇个体对应的Si作为平滑因子σ带入GRNN模型中，带入训练样本得到神经网络模型，并计算训练样本的网络预测值与试验值的RMSE，并以此作为各果蝇个体位置的味道浓度Smelli.

5) 找到果蝇群体中味道浓度Smelli最优个体，即RMSE最小值，判断味道浓度是否优于前一次迭代味道浓度，保留最佳平滑因子σ值与对应的位置坐标(U0,V0).

[bestSmellibest]=max (Smelli)，

(10)

U0=Uibest，

(11)

V0=Vibest，

(12)

σ=Sibest.

(13)

6)判断时候达到最大迭代次数，已达到则执行步骤7；未达到则果蝇群体利用视觉往该位置(U0,V0)飞去，g=g+1，进行迭代寻优，重复执行步骤2～步骤5.

7)将最优平滑因子σ值带入GRNN模型并输出测试样本预测结果。

2 计算分析与讨论

2.1 基于试验数据最佳平滑因子计算

基于表1与表2的试验数据在Matlab 2010a环境下进行仿真实验。以表1中1～4组的20个样本作为训练样本，表2中3组数据分别作为测试样本，

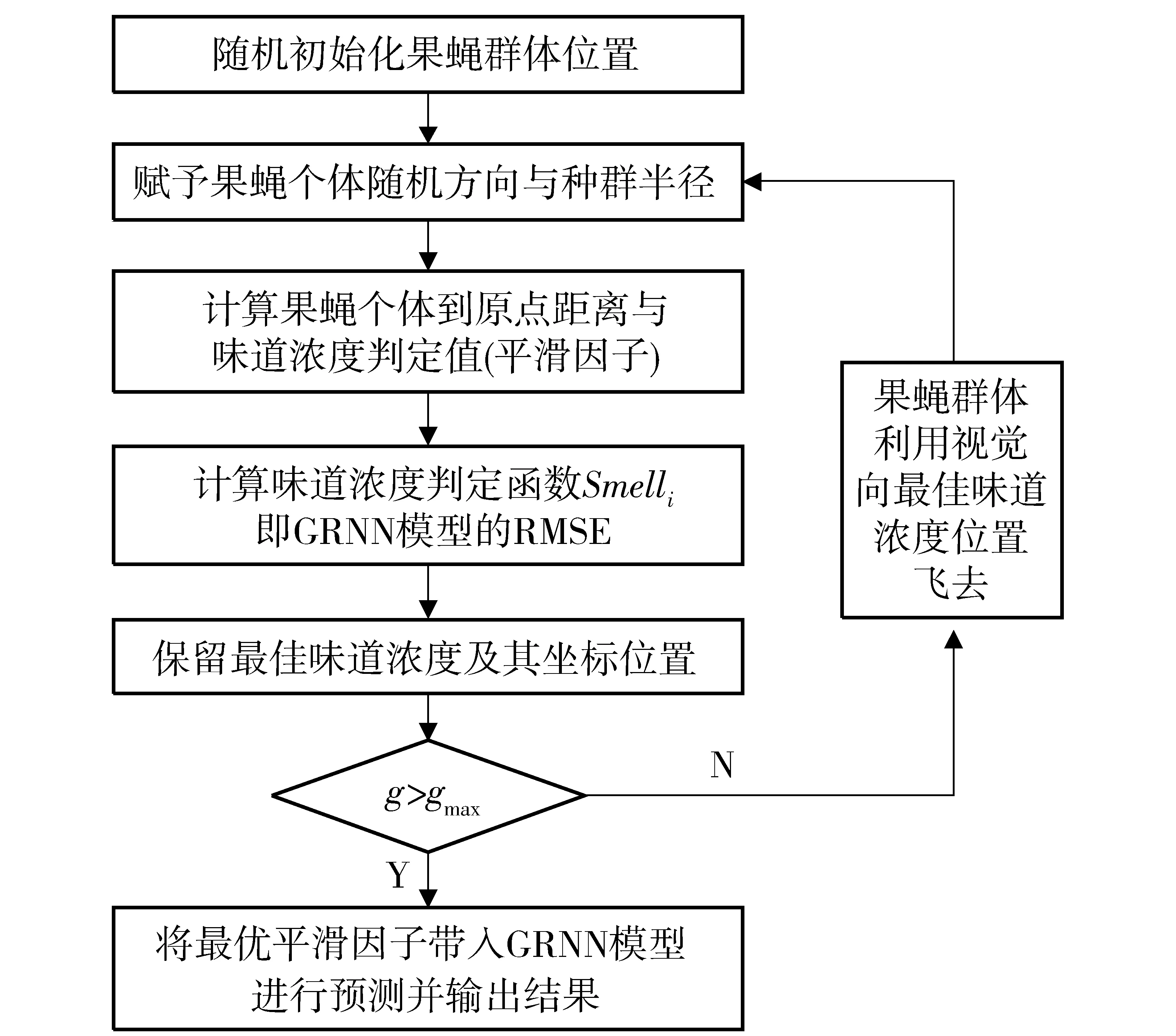
图2 FOAGRNN流程图Fig.2 Flowchart of FOAGRNN model

数据的环境温度、射击间隔与累计射弹量为输入样本，相对初速为输出样本。

将20个训练样本平均分为两组带入到基于FOAGRNN的机枪枪管初速衰减预测模型中进行交叉训练，设定果蝇群体的最大迭代次数gmax=50，种群个体数量为Nsp=30，果蝇飞行方向和距离区间设定为[-1,1]，初始的平滑因子σ由算法自动产生。以训练样本的网络预测值与试验值的均方差为味道浓度判定函数，均方差越小越好。经过50次迭代后，最终确定的最佳平滑因子σ值为53.4.

表2 测试样本的预测结果与误差Tab.2 Predicted results and errors of test samples

2.2 测试样本的初速衰减预测和试验对比分析

将计算得到的最佳平滑因子代入初速衰减预测模型中，得到对3组测试样本的预测结果。图3～图5分别为测试样本的预测结果与试验值的对比图，结合表2可以看出，基于FOAGRNN的机枪枪管初速衰减模型的预测结果与试验结果是基本一致的，3组结果的平均相对误差仅为1.224%.

图3 FOAGRNN预测模型对第1组测试样本的预测结果图(环境温度22 ℃、射击间隔时间1.0 min)Fig.3 Predicted results of FOAGRNN for test samples in Group 1(ambient temperature: 22 ℃;shooting interval: 1.0 min)

图4 FOAGRNN预测模型对第2组测试样本的预测结果图(环境温度22 ℃、射击间隔时间2.0 min)Fig.4 Predicted results of FOAGRNN for test samples in Group 2(ambient temperature: 22 ℃;shooting interval: 2.0 min)

图5 FOAGRNN预测模型对测试样本3的预测结果图(环境温度-25 ℃、射击间隔时间2.0 min)Fig.5 Predicted results of FOAGRNN for test samples in Group 3(ambient temperature: -25 ℃;shooting interval: 2.0 min)

以初速下降量达到15%作为判断机枪枪管寿终的标准，即相对初速达到0.85时对应的累计射弹量可作为寿终射弹量。表3中给出了FOAGRNN预测模型对3组测试样本中机枪枪管寿终射弹量的预测情况。

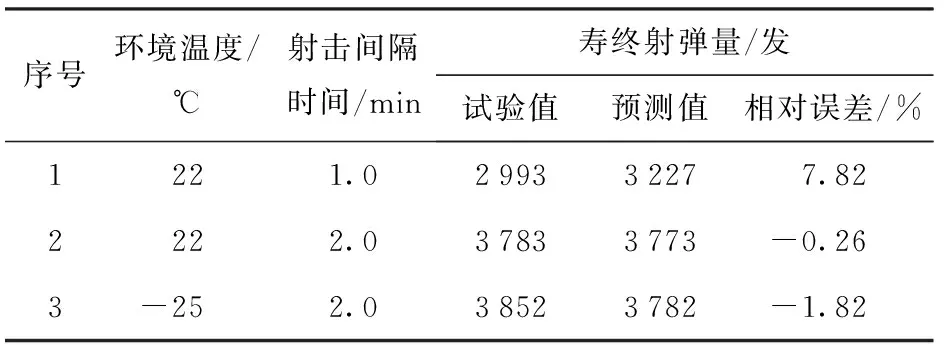
表3 FOAGRNN预测模型机枪枪管寿命预测结果Tab.3 Predicted results of FOAGRNN for barrel life

2.3 FOAGRNN模型、GRNN模型和BPNN模型比较

本文还建立了未经优化的GRNN模型与BPNN模型对上述数据进行预测，并与FOAGRNN模型的预测结果进行比较。

未经优化的GRNN模型取平滑因子为1进行训练。BPNN采用3层网络结构，输入变量有3个：试验环境温度、射击间隔时间与累计射弹量，因此输入层节点取3，隐含层取7个节点，仅有相对初速1个输出变量，故输出层的节点数取1，各层均采用“tansig”传递函数，经10 000次迭代完成训练并输出结果。

将训练样本分别输入完成训练的3种模型中，得到了3种模型对训练样本的预测结果与相对误差(见表4)。图6为3种模型对训练样本的预测结果与试验值的对比，图7中比较了3种模型对训练样本的预测值与试验值的相对误差。通过对表4分析可得，3种模型对训练样本的预测值的相对平均偏差分别为0.647%、0.057%与1.910%. 从中可以看出，FOAGRNN模型与未经优化的GRNN模型对训练样本的拟合能力明显好于BPNN模型。

表4 FOAGRNN模型、GRNN模型与BPNN模型对训练样本的预测结果与相对误差Tab.4 Predicted results and errors of FOAGRNN, GRNN and BPNN models for training samples

图6 FOAGRNN模型、GRNN模型与BPNN模型对训练样本的预测结果Fig.6 Predicted results of FOAGRNN, GRNN and BPNN models for training samples

图7 FOAGRNN模型、GRNN模型与BPNN模型对训练样本预测值的相对误差Fig.7 Predicted errors of FOAGRNN, GRNN and BPNN models for training samples

3种模型分别对3组测试样本的预测结果与试验值比较及相对误差比较，如图8～图13所示。通过对表2分析可得，3种模型对测试样本的预测值的相对平均偏差分别为1.224%、33.897%与1.975%.

由此可以看出，虽然未经优化的GRNN模型的拟合能力较强，但其预测能力有限，FOAGRNN模型与BPNN模型对测试样本的预测结果明显好于未经优化的GRNN模型。结合表2与表4中的数据，3组测试样本的结果均表明FOAGRNN模型的预测能力明显优于另外两种方法。

综合考虑3种模型对训练样本的拟合能力与对测试样本的预测能力，可以看出，FOAGRNN模型的精度最高，能够适应于机枪枪管初速衰减建模。

图8 FOAGRNN模型、GRNN模型与BPNN模型对第1组测试样本的预测结果(环境温度22 ℃、射击间隔时间1.0 min)Fig.8 Predicted results of FOAGRNN, GRNN and BPNN models for test samples in Group 1 (ambient temperature: 22 ℃; shooting interval: 1.0 min)

图9 FOAGRNN模型、GRNN模型与BPNN模型对第1组测试样本预测值的相对误差(环境温度22 ℃、射击间隔时间1.0 min)Fig.9 Predicted relative errors of FOAGRNN, GRNN and BPNN models for test samples in Group 1(Ambient temperature: 22 ℃; shooting interval: 1.0 min)

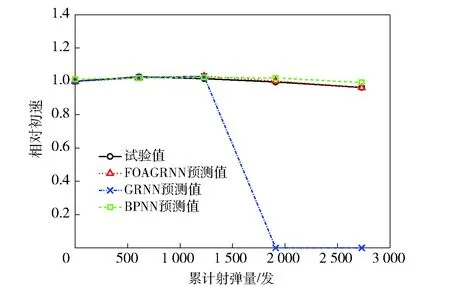
图10 FOAGRNN模型、GRNN模型与BPNN模型对第2组测试样本的预测结果(环境温度22 ℃、射击间隔时间2.0 min)Fig.10 Predicted results of FOAGRNN, GRNN and BPNN models for test samples in Group 2(ambient temperature: 22 ℃; shooting interval: 2.0 min)

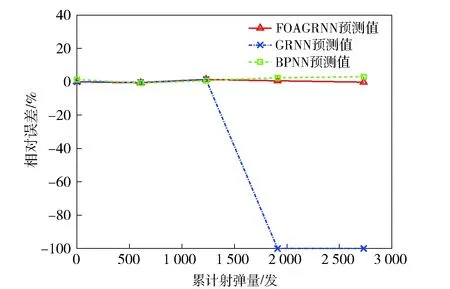
图11 FOAGRNN模型、GRNN模型与BPNN模型对第2组测试样本预测值的相对误差(环境温度22 ℃、射击间隔时间2.0 min)Fig.11 Predicted relative errors of FOAGRNN, GRNN and BPNN models for test samples in Group 2 (ambient temperature: 22 ℃;shooting interval: 2.0 min)

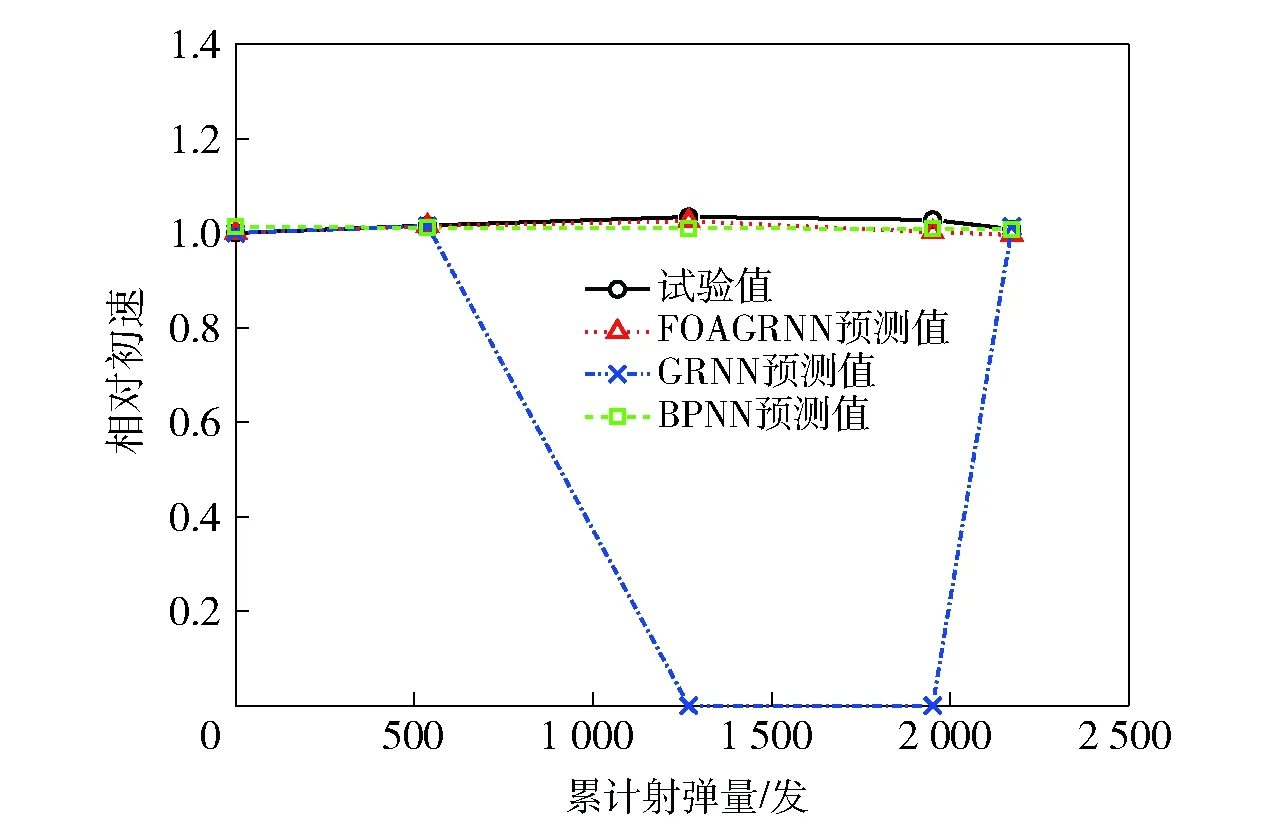
图12 FOAGRNN模型、GRNN模型与BPNN模型对第3组测试样本的预测结果(环境温度-25 ℃、射击间隔时间2.0 min)Fig.12 Predicted results of FOAGRNN, GRNN and BPNN models for test samples in Group 3(ambient temperature: -25 ℃; shooting interval: 2.0 min)

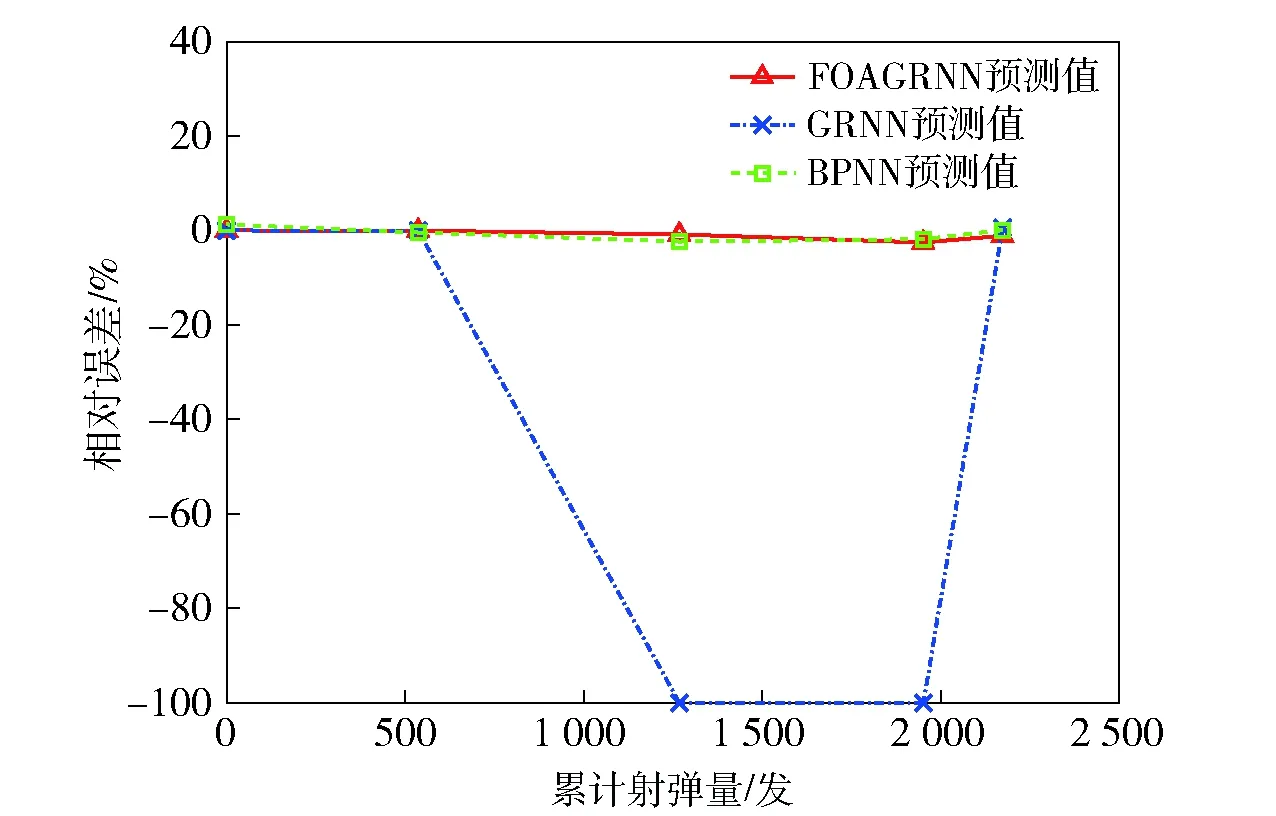
图13 FOAGRNN模型、GRNN模型与BPNN模型对第3组测试样本预测值的相对误差(环境温度-25 ℃、射击间隔时间2.0 min)Fig.13 Predicted relative errors of FOAGRNN, GRNN and BPNN models for test samples in Group 3(ambient temperature: -25 ℃; shooting interval: 2.0 min)

3 结论

本文提出了基于FOAGRNN建立机枪枪管初速衰减模型的方法；基于机枪枪管初速衰减试验，建立了某大口径机枪枪管在不同使用温度和射击间隔下的初速衰减模型。结果表明，该方法建立的预测模型有很好的预测能力。该模型既能预测机枪枪管初速随射弹量增加的下降情况，又能预测机枪枪管寿命，预测结果与试验值的偏差较小。本文还通过与未经优化的GRNN方法和BPNN方法建立的预测模型进行比较，其性能明显优于另外两种方法，验证了FOAGRNN方法在建立机枪枪管初速衰减模型中的有效性。

References)

[1] 杨明华, 吴东亚, 董玉才,等. 大口径机枪加速寿命试验技术研究[C]∥亚太地区信息论学术会议. 杭州:中国电子学会信息论分会, 2011:360-363. YANG Ming-hua, WU Dong-ya, DONG Yu-cai, et al.The study on the accelerated life test technology of the large-caliber machine gun[C]∥The 2nd Asia-Pacific Conference on Information Theory. Hangzhou:Information Theory Society, Chinese Institute of Electronics, 2011:360-363.(in Chinese)

[2] 张玲, 杨明华, 吴东亚,等. 基于加速寿命试验的大口径机枪寿命理论研究[C]∥亚太地区信息论学术会议. 杭州:中国电子学会信息论分会, 2011:86-89. ZHANG Ling, YANG Ming-hua, WU Dong-ya, et al. Research on thetechnology of accelerated life test of the large-caliber machine gun[C]∥The 2nd Asia-Pacific Conference on Information Theory. Hangzhou:Information Theory Society, Chinese Institute of Electronics, 2011:86-89.(in Chinese)

[3] 陈国利, 韩海波, 于东鹏. BP神经网络的身管寿命预测方法[J]. 火力与指挥控制, 2008, 33(9):146-148. CHEN Guo-li, HAN Hai-bo, YU Dong-peng.Prediction method of barrels’ life based on BP neural network[J]. Fire Control and Command Control, 2008, 33(9):146-149.(in Chinese)

[4] 张军, 单永海, 曹殿广,等. 基于最小二乘支持向量机的机枪加速寿命建模[J]. 兵工学报, 2012, 33(1):63-68. ZHANG Jun, SHAN Yong-hai,CAO Dian-guang, et al. Accelerated life modeling for machine gun based on LS- SVM[J]. Acta Armamentarii, 2012, 33(1):63-68.(in Chinese)

[5] 单永海, 张军, 王全正,等. 机枪身管常温综合寿命试验技术研究[J]. 兵工学报, 2013, 34(1):1-7. SHAN Yong-hai, ZHANG Jun, WANG Quan-zheng, et al.Study on lifetime test for machinegun barrel in normal temperature[J]. Acta Armamentarii, 2013, 34(1):1-7.(in Chinese)

[6] 方峻, 吴华晴. 融合理论退化模拟与试验数据的身管寿命预测[J]. 机械科学与技术, 2014, 33(10):1468-1472. FANG Jun，WU Hua-qing. Prediction of the barrel life based on the theoretical degradation simulation and the experimental data[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33(10):1468-1472.(in Chinese)

[7] Specht D F. A general regression neural network[J]. IEEE Transactions on Neural Networks, 1991, 2(6):568-576.

[8] Övünç Polat, Tülay Yldrm. Genetic optimization of GRNN for pattern recognition without feature extraction[J]. Expert Systems with Applications, 2008, 34(4):2444-2448.

[9] Xia C H, Lei B J, Wang H P, et al. GRNN short-term load forecasting model and virtual instrument design[J]. Energy Procedia, 2011, 13:9150-9158.

[10] 潘文超. 应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J]. 太原理工大学学报:社会科学版, 2011, 29(4):1-5. PAN Wen-chao.Using fruit fly optimization algorithm optimized general regression neural network to construct the operating performance of enterprises model[J]. Journal of Taiyuan University of Technology: Social Science Edition, 2011, 29(4):1-5.(in Chinese)

[11] 王海军, 涂凯, 闫晓荣. 基于果蝇优化算法的GRNN模型在边坡稳定预测中的应用[J]. 水电能源科学, 2015, 33(1):124-126. WANG Hai-jun, TU Kai, YAN Xiao-rong. Application of general regression neural network to predict slope stability based on fruit fly optimization algorithm[J]. Water Resources and Power, 2015, 33(1):124-126.(in Chinese)

[12] 王英博，聂娜娜，王铭泽，等. 修正型果蝇算法优化GRNN网络的尾矿库安全预测[J]. 计算机工程, 2015，41(4):267-272. WANG Ying-bo, NIE Na-na, WANG Ming-ze, et al. Mine tailings facilities safety evaluation of GRNN optimized by modified fruit fly algorithm[J]. Computer Engineering, 2015，41(4):267-272. (in Chinese)

[13] 张燕君, 刘文哲, 付兴虎, 等.基于自适应变异果蝇优化算法和广义回归神经网络的布里渊散射谱特征提取[J]. 光谱学与光谱分析, 2015，35(10):2916-2923. ZHANG Yan-jun, LIU Wen-zhe, FU Xing-hu, et al. A Brillouin scattering spectrum feature extraction based on flies optimization algorithm with adaptive mutation and generalized regression neural network[J]. Spectroscopy and Spectral Analysis, 2015，35(10):2916-2923. (in Chinese)

[14] Pan W C. A new fruit fly optimization algorithm: taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26(2):69-74.

Modeling and Prediction of Muzzle Velocity Degradation of Machine Gun Based on FOAGRNN

CAO Yan-feng, XU Cheng

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)

Muzzle velocity degradation prediction of machine gun is a complicated non-linear problem. Generalized regression neural network (GRNN) has been widely used in the modeling of the non-linear problems, but GRNN has rarely been used to predict the muzzle velocity degradation of machine gun. Since the smoothing factor of GRNN obviously affects the prediction performance of neural network, the fruit fly optimization algorithm is used to automatically select the parameters of GRNN. A method to model a muzzle velocity degradation based on general regression neural network with fruit fly optimization algorithm (FOAGRNN) is proposed. A prediction model is established based on the experimental data of muzzle velocity degradation, in which the muzzle velocity degradation is taken as characteristic quantity. The predicted results are basically consistent with the experimental results. The research result shows that FOAGRNN model outperforms GRNN model with default parameter and BPNN prediction model in the prediction of muzzle velocity degradation.

ordnance science and technology; fruit fly optimization algorithm; generallized regression neural network; muzzle velocity degradation; prediction model

2016-04-19

国家自然科学基金项目(51575279)

曹岩枫(1988—)，男，博士研究生。E-mail:caoyf2010@163.com

徐诚(1962—)，男，教授，博士生导师。E-mail:xucheng62@163.com

TJ25

A

1000-1093(2017)01-0001-08

10.3969/j.issn.1000-1093.2017.01.001