理想流体的法拉第波模态
2017-02-18赵文定王思慧范周游程恩泽周惠君高文莉
赵文定,王思慧,范周游,程恩泽,周惠君,高文莉
(南京大学 物理学院,江苏 南京 210093)

理想流体的法拉第波模态
赵文定,王思慧,范周游,程恩泽,周惠君,高文莉
(南京大学 物理学院,江苏 南京 210093)
研究了理想流体的法拉第波模态. 由法拉第波的振幅方程给出了稳定条件下的色散关系,利用参量共振方程得到了在亚简谐条件下本征波矢的取值范围. 引入几何模型,在一定实验条件下,可以简单而直观地预测模态及其花纹图案. 解释了不同模态的竞争情况,对比分析了相图关系的理论预测结果,几何模型的预测与实验及理论计算结果相符合.
法拉第波;亚谐振;色散关系;Mathieu方程;几何模型
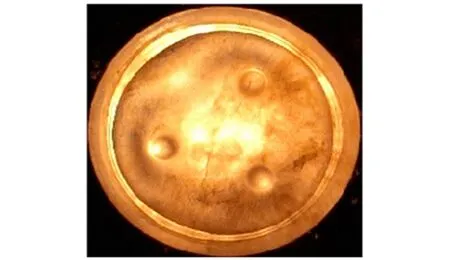
法拉第波是日常生活中常见的现象,如图1所示,当装有液体的刚性容器受到垂直振动激励时,在其自由液面上会产生出稳定的波纹形状,这种现象被称为法拉第现象[1]. 至今,人们对法拉第波,尤其是在理想流体下的法拉第波进行过多方面的研究.

图1 法拉第波实验现象
Rayleigh[2]做了类似的实验,发现表面波的频率是垂直激励频率一半,并发现与驱动参量有关,但是没有给出数学上的解释. 1954年,Benjanmin和Uresell共同给出了理想流体法拉第波在小振幅下的理论解析解[3],他们从流体Eular 方程导出振幅公式,发现理想流体在小振幅的情况下满足Mathieu方程,并指出表面波的响应频率可能存在亚简谐共振、简谐共振、超谐共振等.
关于法拉第波的非线性行为,Gollub和Meyer[4]在实验中很清晰地观察到2个模式竞争的情况. Ockendon[5]从理论上研究了分岔结构,并且定性地研究了线性阻尼的影响. Miles[6]则提出在单模态下利用哈密顿函数表述和线性近似来求解法拉第波. Ciliberto和Gollub[7]为了解释观察到的混沌行为,提出了动力系统的振幅模型方程,并通过数值积分得到了具有周期或者混沌的解. 基于前人的工作Umeki 和Kambe[8]通过数值计算给出了相平面上的周期和混沌轨道. 未查到将激励参量等条件和实空间中的波纹形状联系的文献.
本文回顾了理想流体法拉第波的理论解,提出了法拉第波的色散关系,进而在亚简谐条件下利用参量共振给出了本征值km的范围. 提出用于预测法拉第波表面花纹形态的几何模型,并且解释了实验中出现的多模态竞争现象. 我们认为:法拉第波的表面振动是由若干个本征振动叠加而成的,而且本征振动模态对应的本征值在参量共振允许范围之内. 我们提出的几何模型将本征波矢km和实空间下花纹图案联系起来. 通过对不同驱动参量下的实验数据的定性分析,给出了关于参量频率f、振幅A的相图以及理论预测和实验值的拟合图像,实验结果与理论预测结果基本符合.
1 理论分析
1.1 理想流体理论回顾
通常描述理想流体法拉第波的流体力学方程为[3]
γρ∂2ξ∂x2+∂2ξ∂y2+∂φ∂tz=0-[g-Fcos (Ωt)]ξ=0,
(1)
其中,g为重力加速度,Fcos (Ωt)为振台垂直振动的加速度,ρ为液体密度,γ为表面张力系数,ξ为竖直方向上位移,φ为流势. 对于圆柱容器,根据边界条件可知,振幅方程可由贝塞尔函数Sl,m作为基底做无穷级展开:
ξ(x,y,t)=∑∞0al,m(t)Sl,m(x,y),
(2)
其中,l和m是本征值序数,为了简化只使用m表示,x和y为平面坐标,t为时间,al,m为含时的调幅因子(后简化写为am),Sl,m(x,y)是在边界条件下确定的特征函数. 代入方程(1) 中可以得出对系数有如下要求:
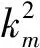
(3)
其中,h为液体深度,km为用基底(如Bessel函数)表达振幅时对应的本征值.
本文重点研究亚简谐下法拉第波的稳定性以及激励参量与模态和波纹形状的关系.
1.2 色散关系和本征模态
方程(2)中的Sl,m给出了法拉第波的本征模态,当实验参量满足该模态被激发的条件时,该模态被激发.
法拉第波出现稳定模态的色散关系应该不含时间项,由方程(3)可知对应的色散关系为

(4)
法拉第波中稳定模态与连续流体介质中的表面波具有相同的色散关系,因此波速为
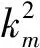
(5)
波长为
λm=2πcω=2πkm.
(6)
式(4)~(6)给出了一定频率的法拉第波对应的波长和波速,km具有波矢的意义.
当频率和外激励满足一定条件时,本征模态会被激发,由此可以导出相应的花纹,以下从参量共振方程的稳定性出发,导出亚简谐条件下法拉第波模态被激发的条件.
1.3 法拉第波的亚简谐参量共振
为了描述法拉第波在外激励下的响应,尤其是发生共振的条件,考虑时间响应,把方程(3) 改写为

(7)

方程(7)具有Mathieu方程的形式,以下分析它描述的参量共振的条件[9].
从Mathieu方程的稳定性相图分析中可知,该方程的解应该存在于不同的参量共振区域,即亚简谐、简谐或超简谐共振. 在实验中观察到出现最多的是亚谐振情况,也就是说Ω=2ω0,同样从理论预测中可以得到亚谐振的稳定区域将会大于谐振或超谐振区域,因此仅在亚谐振情况下求解该问题.
设Ω=2ω0+Δω(Δω≪ω0),代入式(7), 得:

(8)
观察式(8),可以期望方程有如下形式的解:
am(t)=a(t)cosω0+12Δωt+
b(t)sinω0+12Δωt,
(9)
将式(9)代入式(8)中并利用和差化积公式得
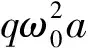
cosω0+12Δωt+d2bdt2-bω0Δω-b12Δω2+
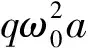
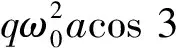

(10)
由于主要考虑亚谐振的情况,那么忽略3ω0+12Δω的部分以及二阶小量,同时方程要求对于任意时刻t都成立,所以可以得到如下方程组:
12qω0-Δωa+2dbdt=0,
2dadt+12qω0-Δωb=0.
再将a=a0elt,b=b0elt代入方程组得到:
12qω0-Δωa0+2lb0=0,
2la0+12qω0-Δωb0=0.
若要a0和b0有非零解,要求
l2=1412qω02-(Δω)2,
(11)
l为实数,可知在亚简谐下发生参量共振所要求的条件是
2ω0-12qω0<Ω<2ω0+12qω0.
(12)

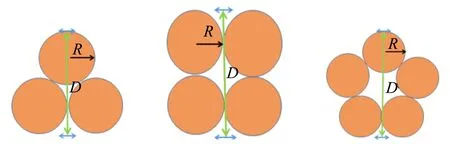
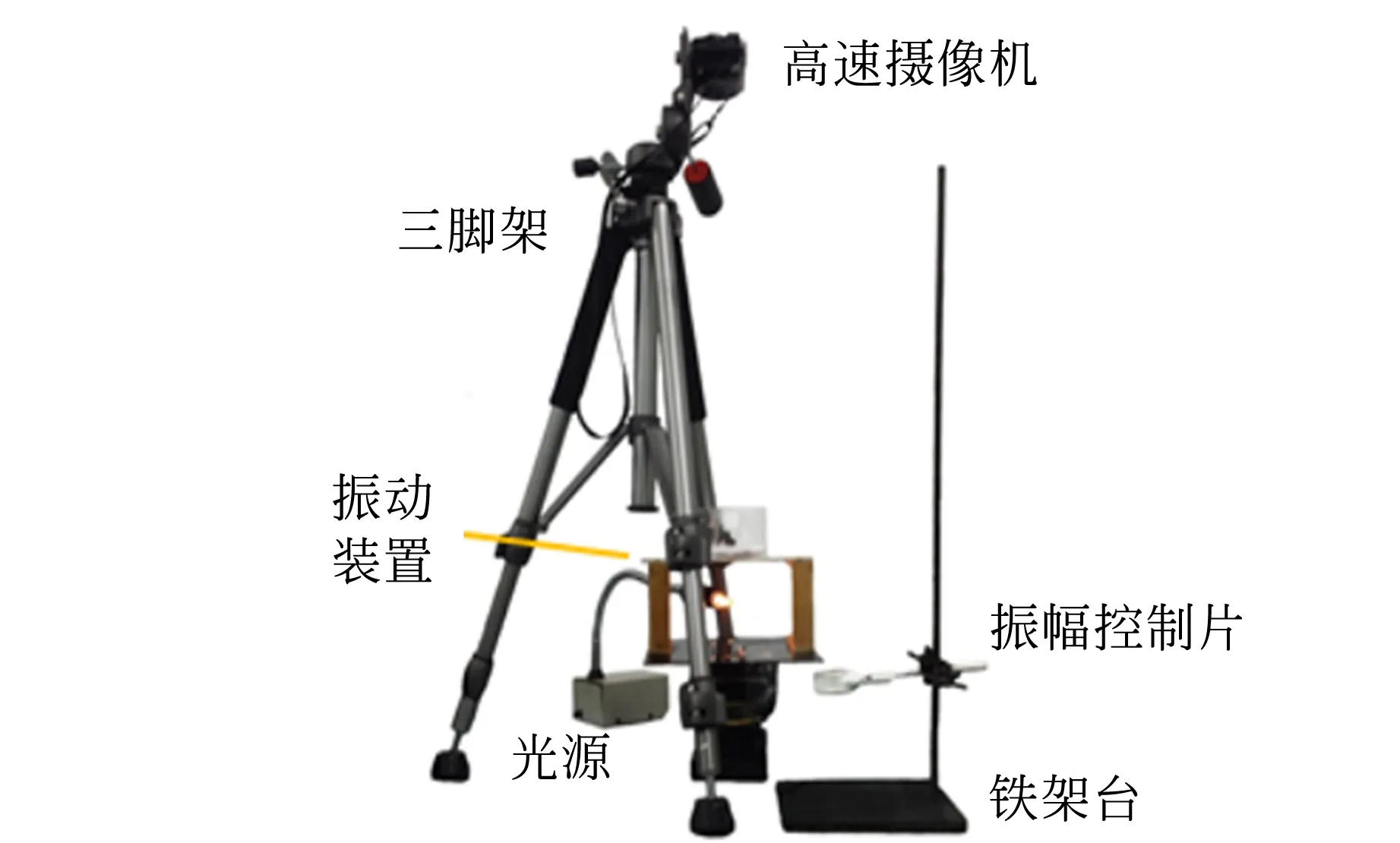
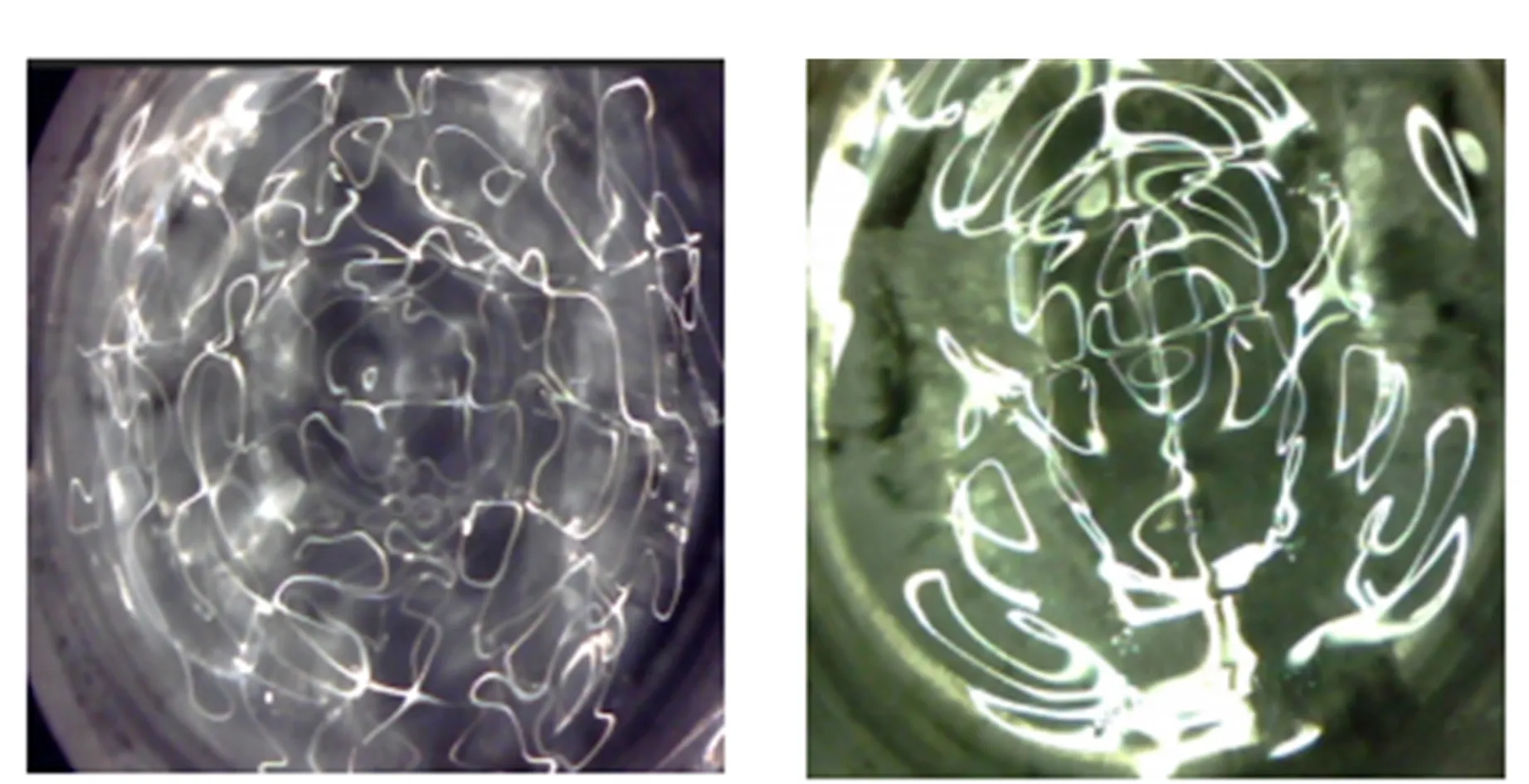
f1(F,Ω) (13) 由于式(13)没有解析解,其数值解见图2,2条曲线分别为km上下限随频率变化图像,圆点分别为(3,10)(4,8)模态. 图2 (13)式数值解 1个波矢km对应于1个本征模态的基底Sm,n. 由不等式(13)及图2可得知在激励参量F和Ω一定的条件下,波矢km的取值存在一定的范围,所以一定条件下可能出现多模态共存现象. 例如,圆柱容器直径D=10 cm,水深h=1 cm,激励频率f=34.8 Hz,振幅A=0.01 m,观察到(m,n)=(3,10),(4,8)2种振动模态,如图2所示,其本征函数Sm的本征值km分别为22.0和24.2. 由不等式(13) 解出的km范围为22.4~24.8,实验结果与理论预测范围基本吻合. 实空间中观察到的花纹是单个或多个本征振动模态叠加的结果,以下引入几何模型以便直观地表达法拉第波花纹和激励条件等实验参量之间的联系. 1.4 法拉第波的几何模型 根据式(2),液体竖直方向位移包含2部分:随时间变化调幅因子是am(t),其空间分布由基底函数Sm,n(x,y)决定. 对于圆柱容器单模态,它的解是Bessel 方程相应的花纹图案随时间的振荡调制. 因此可以通过模态的函数图像得出实空间对称轴和波峰个数等. 例如,在圆柱容器直径D=4.6 cm,水深h=0.5 cm,频率f=20 Hz条件下,对应解的本征函数是贝塞尔函数S1,3,其二维图像如图3所示,有3个对称的波峰和波谷. 在图3中液体的竖直方向上的位移高度是通过颜色来表示的,红色说明高于水平面的波峰,而蓝色则是低于水平面的波谷,深浅说明振幅大小. 在相同的条件下得到的实验结果见图3(c),与理论预测结果一致. (a)模拟波峰 (b)俯视图 (c)实验结果图3 计算机模拟3个波峰及实验结果 下面引入几何模型,描述波峰的数量以及对称性,同时推测一定条件下法拉第波呈现何种模态. 将km对应的波长为直径的圆形作为波峰圆,Bessel函数在径向上有m个零点,其间隔是波长,而在圆周方向上会以2π/n作周期重复,即在圆周方向上有n个波峰(n次旋转轴). 因此可以假设波峰排布满足以下规则: 1)排布方式围绕中心有n次对称轴. 2)每层的波峰个数相同. 3)在选取不同模态时尽可能满足面积利用率较大,即波峰圆占据容器大部分面积. 根据容器直径和波峰圆的面积可以计算出密排时的波峰个数N,N是实际波峰个数的上限. 按照轴向对称性和径向排布规则的要求,可以将N因数分解为满足N≈m×n的若干组(m,n),对应于可能出现的模态. 以圆柱容器中单层排布为例,如图4所示,不同排布模式下排成1层所需要的最小容器直径D是不同的,其满排直径分别为D3=43+63R,D4=4R,D5=4Rsin 3π10+2R,D6=6R,等等. 波峰圆半径R为波长一半. 当排布直径和容器直径接近时,该模态将可能被观察到. (a)(1,3)模态 (b)(1,4)模态 (c)(1,5)模态图4 单层情况下对于不同n值的排布直径 对于多层排列,以S(2,6)为例,同样符合上述规则,如图5所示. 图5 (2,6)模态的示意图 当一定实验条件下只存在1个模态时,该振动模态是稳定的. 如果同时存在多种模态,会出现模态之间竞争,甚至出现混沌. 图6是实验装置图,包括振动平台、连接PASCO 波形驱动器、盛放液体的圆柱容器. 在振台上镶嵌有钢针,用于限位和测量振幅. 图像由Casio 高速摄相机(EXZR 200)记录. (a)实验装置 (b)振台与容器图6 实验仪器 2.1 单层下波峰个数 表1是根据几何模型计算的波峰个数和实验结果的对照. 考虑到不同对称轴的情况下面积占用率是不同的,在计算时引入等效密排面积对容器面积做了修正: S′=αS, (14) 其修正系数α是多边形与外接圆面积的比值. 表1表明:几何模型预测的波峰数和实验结果吻合. 表1 理论预测波峰个数N和实验结果对比表 2.2 模态竞争与共存 在法拉第波的实验中,经常有不同模态交替出现的情况,称之为模态竞争现象,例如表1 中在激励频率为23 Hz 时,(1,6)和(1,8)模态共存. 接下来以实例对模态竞争情况进行分析. (a)(3,10) (b)(4,8)图7 f=34.8 Hz, A=1 cm时,交替出现(3,10)和 (4,8)模态的实验图像 实验中,在振台频率f=34.8 Hz、振幅A=1 cm时,观察到2个模态(3,10)和(4,8)交替出现(图7). 由背景照射光反射规律,可以大致推断出各个亮纹(亮度大约一致)所包围的连通闭合区域构成1个波峰圆. (因为拍摄和入射光角度等原因,波峰圆的形状有变形且明暗不一致.) 在实验参量下,利用式(2)和(3)计算,同样可以得到2个模态(3,10)和(4,8)的理论图像(图8),与实验图像相符合. (a)(3,10) (b)(4,8)图8 (3,10)和(4,8)模态对应的计算模拟图像 接下来验证几何模型,根据图2给出的范围推算出的可能波长,再按照几何模型的规则预测模态,同样可以得到2个模态(3,10)和(4,8)在该条件下存在. 在水深远小于波长且激励振幅较小时,同时忽略表面张力项,式(4)退化为浅水波公式,可以简化对于法拉第波的描述方式. 图9是改变激励频率和振幅得到的相图,其中数据点是实验结果,实线是理论计算结果,混沌和竞争没有明确的分界,图中的虚线是示意. 表明了2个模态各自单独存在和共存的条件以及形式. 在频率较小时出现稳定的(3,10)单模态,当频率较大时(4,8)单模态稳定存在,在中间频率段存在2个模态的竞争,且激励振幅增大时会出现混沌现象. 图9 (3,10)(4,8)模态对应的相图 由法拉第波的振幅方程给出了稳定条件下的色散关系,利用参量共振方程得到了在亚简谐条件下本征波矢km的取值范围. 提出了几何模型,在一定实验条件下,可以简单而直观地预测模态及其花纹图案,几何模型的预测与实验及理论计算结果相符合. [1] Faraday M. On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces [J]. Philosophical Transactions of the Royal Society of London, 1831,121:299-340. [2] Rayleigh L. XXXIII. on maintained vibrations [J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1883,15(94):229-235. [3] Benjamin T B, Ursell F. The stability of the plane free surface of a liquid in vertical periodic motion [J]. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 1954,225(1163):505-515. [4] Gollub J P, Meyer C W. Symmetry-breaking instabilities on a fluid surface [J]. Physica D: Nonlinear Phenomena, 1983,6(3):337-346. [5] Ockendon J R, Ockendon H. Resonant surface waves [J]. Journal of Fluid Mechanics, 1973,59(2):397-413. [6] Miles J W. Nonlinear faraday resonance [J]. Journal of Fluid Mechanics, 1984,146:285-302. [7] Ciliberto S, Gollub J P. Chaotic mode competition in parametrically forced surface waves [J]. Journal of Fluid Mechanics, 1985,158:381-398. [8] Umeki M, Kambe T. Nonlinear dynamics and chaos in parametrically excited surface waves [J]. Journal of the Physical Society of Japan, 1989,58(1):140-154. [9] 梁昆淼. 理论力学(下册)[M]. 3版. 北京:高等教育出版社,1992:176-178. [责任编辑:任德香] Vibrating modes of Faraday waves in ideal fluid ZHAO Wen-ding, WANG Si-hui, FAN Zhou-you, CHEN En-ze, ZHOU Hui-jun, GAO Wen-li (School of Physics, Nanjing University, Nanjing 210093, China) The Faraday wave patterns and corresponding vibrating modes in ideal fluid were studied theoretically and experimentally. The dispersion relation had been got by deriving the amplitude equations of Faraday waves. The range of eigenvalue was also calculated based on the parametric resonance theory. To predict possible patterns in real space, a geometric model on the basis of experimental parameters was proposed, which could intuitively predict the different wave patterns and the conditions of mode competitions. The experimental phase diagram was also analyzed. A good agreement between the measured and theoretical results was obtained. Faraday waves; sub-harmonic resonance; dispersion relation; Mathieu equations; geometric model 2016-05-29;修改日期:2016-09-01 南京大学国家级创新计划(No.G201510284029) 赵文定(1995-),男,上海人,南京大学物理学院2013级本科生. 指导教师:王思慧(1964-),女,北京人,南京大学物理学院教授,博士,主要从事基础物理理论与实验教学研究. O353 A 1005-4642(2017)01-0013-06 “第9届全国高等学校物理实验教学研讨会” 论文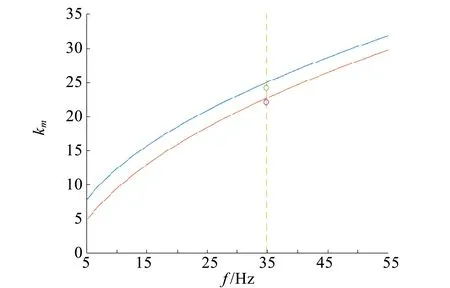



2 实验验证




3 结束语
