衍射图形的新型光阑设计和再现实验

张天宁，周望威，吕剑锋，陈 星

(浙江大学 物理学系，浙江 杭州 310027)

衍射图形的新型光阑设计和再现实验

张天宁，周望威，吕剑锋，陈 星

(浙江大学 物理学系，浙江 杭州 310027)

用蒙特卡洛和贪心两者结合混合算法，根据光阑和入射光束波长设计出相应的光阑求解出衍射图案. 在菲涅耳衍射的情形下，对目标图案设计了动态实验仿真窗口，通过加入蒙特卡洛退火元素的混合算法对目标图案进行反演计算,得到光阑编码图像，用扩束准直光路系统实验验证了设计正确性.

光阑;菲涅耳衍射;蒙特卡洛算法;贪心算法

假如光阑的形状和入射光束的波长已知，可以求解衍射图案，但是其逆过程，需要进行反演计算[1]，在理论上比较困难. 虽然在菲涅耳衍射的情形下，可以利用贪心算法通过多次迭代得到期望的简单衍射图案[1-2]，但对分辨率较高较为复杂衍射图案，进行多次迭代，运算时间很长，实时再现较差. 本设计方案加入蒙特卡洛退火的元素，用蒙特卡洛和贪心两者结合的混合算法对于所期望得到的衍射图案进行反演计算[3]，并建立了参量修改图形用户界面(GUI)动态的实验仿真窗口，界面窗口包含目标图案、距离与分辨率等参量的修改、数值模拟结果和设计好的光阑. 此光阑可加载在空间光调制器LC-SLM上，通过扩束准直光学系统输出衍射图案进行验证，证明此光阑设计方法可行.

1 菲涅耳衍射数值算法

E2(x2,y2,z)= eikziλz∬sE1(x1,y2)exp {ik2z[(x1-

x2)2+(y1-y2)2]},

(1)

式中，E1(x1,y1)，E2(x2,y2,z)为物平面和观测平面的光波复振幅，z为两平面的距离[4-5].

sinc 2ax2λzsinc 2by2λz.

(2)

因为衍射图案的形状只与各点之间的相对光强有关，可以略去因子exp (ikz)/i、令波长λ=1取自然单位，并取a=b, 得到

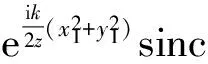
(3)

2 设计模型

2.1 光阑设计

对于1 204a×1 200a的长方形, 将其等分为602×600, 共计361 200个正方形小格，每小格的边长2a. 每个小格都会居于 “透光”和 “不透光”2种状态中的1种, 所有“透光”的小正方形，构成了光阑实际透光的部分，决定了光阑的形状. 假设状态为“透光”的正方形小格，中心坐标为(x1,y1). 其产生的衍射光强分布为

E2(x2,y2,x1,y1，z)=4a2zexp{iπz[(x2-x1)2+(y2-

y1)2]}sinc 2a(x2-x1)zsinc 2a(y2-y1)z.

(4)

可用正方形小格中心点的光强，近似代替整个小格的平均光强. (4)式中的x2-x1，y2-y1，所可能取到的值有： ±600a,±598a, …，±2a,0,±598a，±596a, …，±2a, 0.

共计601×599个衍射数据. 建立存放601×599个衍射数据矩阵数组，根据光阑小格和衍射图案小格的相对位置，就可以调用矩阵数组中的相应衍射数据. 菲涅耳数NFF≥1 orNFF≤1都不是我们要的. 选取菲涅耳数NFF=1经过衍射可以叠加出复杂的图案[4-5]. 这时衍射图案主体的尺寸与光阑尺寸保持相同. 目标图案也为1 204a×1 200a的长方形. 同样可分割为602×600, 共计361 200个正方形小格，每小格的边长为2a. 光阑和衍射屏示意图如图1所示.

图1 光阑和衍射屏示意图

2.2 设计思路

1)选择图案转换成二值图，作为目标图案. 因为二值图的像素点只有“1” 和“0”即“透光”和“不透光”中的1种.

2)对光阑中所有的正方形小格随机赋予“透光”或者“不透光”的初始状态.

3)对所有的小正方形进行扫描(遍历). 当扫描(遍历)至某个小正方形时，改变其透光与否的状态，若改变当前状态可使衍射图案更接近于目标图案，则改变该状态，否则维持原状态不变. 即具有贪心的选择性.

4)比较目标图案对所有的光阑进行扫描(遍历)之后，就可以得到接近目标图案的衍射图案,即具有贪心的子结构选择性. 进行多轮这样的遍历，得到贪心算法的最优解——最终衍射图案.

2.3 模拟实验及分析

目标衍射图案以“浙大校徽”为示例,如图2所示. 图案衍射图案与目标图案的接近程度按判据ε值的大小来判断. 对目标图案和实际衍射图案的光强，进行归一化.

目标衍射图案中，透光(白色像素=1)小格的期望光强为Iexp(x2,y2)=1,不透光(黑色像素=0)Iexp(x2,y2)=0.

(a)分辨率602×600图案 (b)运算得到的光阑

(c)模拟再现衍射图案 (d)目标衍射图案图2 目标衍射图案示例

定义归一化后的期望光强I1exp(x2,y2)为：

I1exp(x2,y2)=Iexp (x2,y2)∑x2,y2Iexp (x2,y2)/N,

(5)

其中，N为目标图案的小格数目，本例N=361 200.

某种形状的光阑所产生的衍射图案在衍射屏上处的光强为

I(x2,y2)=∑x2,y2E2(x2,y2,x1,y1，z)2,

(6)

式中∑x2,y2对应于所有处于“透光”状态的光阑小格. 同样对衍射图案在衍射屏上处的光强归一化为

I1(x2,y2)=I(x2,y2)∑x2,y2I(x2,y2)/N.

(7)

衍射图案的形状只取决于相对光强的大小，归一化并不会影响衍射图案的形状.

判据定义ε为

ε≡∑x2,y2(|I1(x2,y2)-I1exp (x2,y2)|2).

用均方误差ε值的大小作为2种图案接近程度的判据. 分辨率较高较为复杂衍射图案，目标图案对所有的光阑进行扫描(全体遍历)并多次迭代. 运算时间较长，实时再现较差. 可以对贪心算法的多次迭代进行优化. 达到同样ε值，用蒙特卡洛方法代替多次迭代，用随机扫描：沿着已有的图像展开搜索，即采样点是在原来点附近随机上下左右各扫描X(设置的取样点数)个点. 加入蒙特卡洛退火的元素，用蒙特卡洛和贪心两者结合的混合算法对于所期望得到的衍射图案进行反演计算[1，3]. 一种全局搜索能力极强的算法, 相应地系统就能够获得摆脱局部能量极小点的机会，并找到更好的、更接近于整体的极小点. 设计编写了简单明了的用户界面(图3)，界面中的可变参量：距离、输出图案尺寸. 全体扫描、多次迭代次数、优化算法参数：随机扫描、迭代次数、 采样点 退火参数等及实验仿真窗口. 输出光阑. 模拟再现图案. 这些参量决定了整个收敛的准确度以及收敛速度的快慢，需要根据ε值不断尝试． 两种图案接近程度. 运行时设横向运行条和纵向运行条可显示扫描进度.

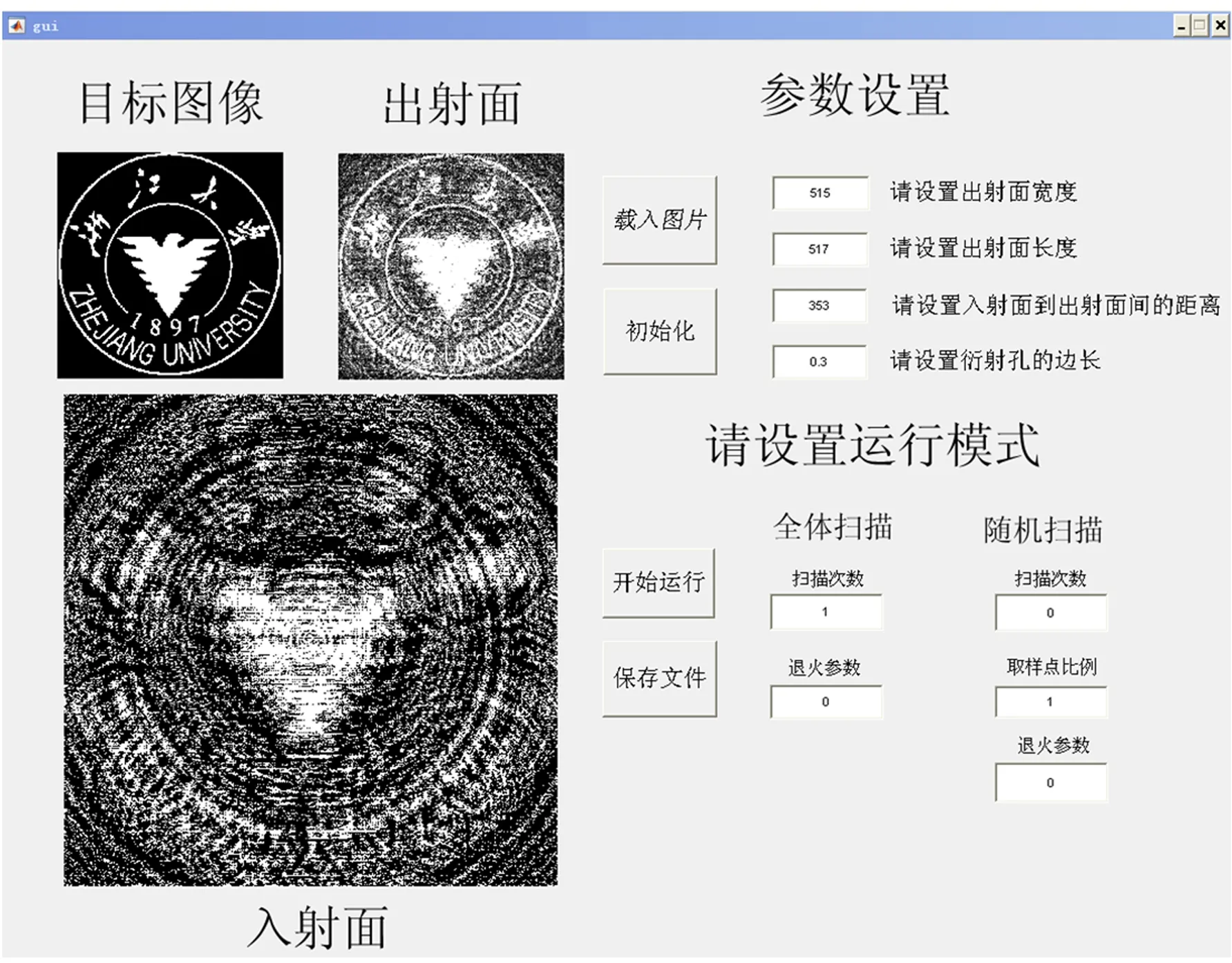
图3 实验仿真窗口用户界面(GUI)

3 光阑的制作和在光学实验中再现

对整个光阑是菲涅耳衍射，对单个像数小正方形是夫琅禾费衍射. 要求是光强均匀分布的平行光. 因为激光器射出的是高斯光束，用扩束准直系统[1，6]由扩束镜、针孔滤波器和傅里叶变换透镜准直镜组成. 将激光细光束扩展为光强均匀分布的平行宽光束. 扩束由显微物镜和针孔组成的滤波器完成，然后经过傅里叶变换透镜的准直镜准直后平行通过起偏器，调节起偏器的角度使入射光的偏振态与空间光调制器一致，然后通过加载了光阑信息的 LC-SLM后,在衍射屏再现目标图案.

4 实验结果与分析

虽然2块透镜组成望远镜系统[2]，也能再现分辨率较低的文字和简单图案. 对分辨率较高的图案，由于光束的不均匀，会导致衍射图案边缘畸变的实验误差. 用图4扩束准直系统：扩束镜和准直镜的焦点重合，构成逆望远镜系统在二透镜共同焦点上放置针孔滤波器，用于高频噪声消除. 光束质量得以提高，获得了宽度大于LC-SLM相面尺寸光强均匀分布的平行光束[1，6]. 实验结果很清晰地表现了分辨率602×600图案目标图案图2(a). 图5为分辨率755×599图案制作光阑和通过图4实验装置图再现目标衍射图案. 从图5(d)实验结果看出图像细节表现得很清晰.

图4 再现目标图案实验装置图

(a)分辨率755×599图案 (b)运算得到的光阑

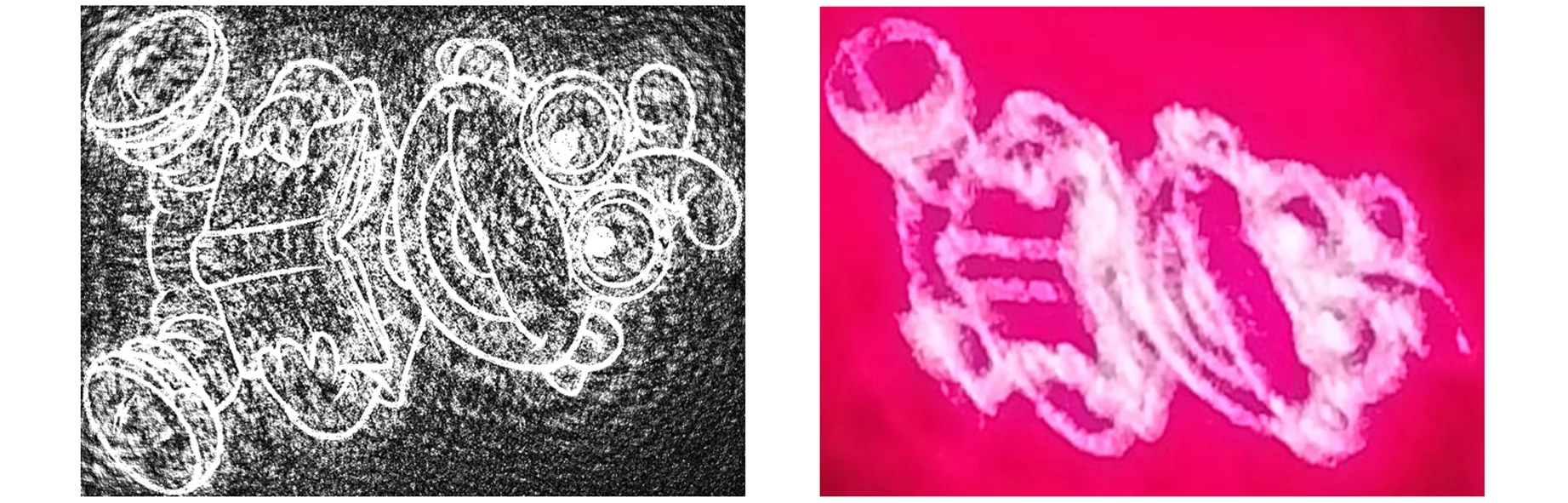
(c)模拟再现衍射图案 (d)实验再现衍射图案图5 再现衍射图案

5 结束语

光阑形状和入射光束的波长已知的正过程是可以求解的，但是其逆过程，在理论上比较困难. 需要进行反演计算. 本实验设计方案先加入蒙特卡洛退火的元素并用蒙特卡洛和模拟退火算法两者相结合的混合算法对复杂衍射图案进行反演计算，从动态模拟实验和光学实验都验证设计的光阑能成功再现目标衍射图案. 建立参量目标图案、距离与分辨率等参量可修改图形用户界面(GUI) 的动态实验仿真窗口. 在光阑制作上分析菲林片和液晶光阀的再现过程，发现相同输出图案尺寸下，分辨率液晶光阀大于菲林片. 再现衍射图案分辨率可达到液晶光阀分辨率，液晶光阀没有菲林片实验误差：光阑孔径偏差，因此光阑制作优选液晶光阀.

[1] 潘安，张晓菲，王彬. 厚样品三维叠层衍射成像的实验研究[J]. 物理学报,2016,65(1):014204-1-16.

[2] Wu Yijia, Cao Shimin, Hua Limin, et al. Design and demonstration of a new kind of apertures for getting expected diffraction patterns [J]. Optics Letters, 2014,39(4):801-804.

[3] 童晟飞，王正忆，陈星. 光学薄膜椭圆偏振数据反演的优化算法[J]. 物理实验,2012,32(9):22-28.

[4] 李俊昌. 衍射计算及数字全息[M]. 北京:科学出版社,2014.

[5] 吕乃光. 傅里叶光学[M]. 2版. 北京:机械出版社,2013.

[6] 杨上供，甘亮勤，熊飞兵. 基于Photoshop的假彩色编码片制作新方法[J]. 激光杂志,2014,35(10):64-66.

[责任编辑：郭 伟]

Design and experiment of new diaphragm to get expected diffraction patterns

ZHANG Tian-ning, ZHOU Wang-wei, LJian-feng, CHEN Xing

(Department of Physics, Zhejiang University, Hangzhou 310027, China)

According to the diaphragm and the wavelength of the incoming light beam, the corresponding apertures were designed to solve the diffraction pattern using a combination of Monte Carlo and greed algorithm. In the regime of Fresnel diffraction, a dynamic simulation window to the target pattern was designed. By joining a blend of elements of the Monte Carlo annealing algorithm, the target pattern was inversely calculated. The coded image of diaphragm was obtained, and the accuracy with the expanded beam collimation light path system was verified by the experiments.

diaphragm; Fresnel diffraction; Monte Carlo algorithm; greedy algorithm

2016-05-27；修改日期：2016-07-14

张天宁(1994-)，男，浙江嵊州人，浙江大学物理学系求是科学班(物理)2013级本科生.

指导教师：陈 星(1962-)，男，浙江杭州人，浙江大学物理学系高级实验师，学士，从事光学、原子结构、核物理等近代物理实验教学与研究．

O436．1

A

1005-4642(2017)01-0048-04

“第9届全国高等学校物理实验教学研讨会”论文