基于费米分布函数的财务预警模型实证研究

宋丽平++李建++张晓杰

【摘 要】 通过引入一种具有统计学原理的费米分布模型对企业财务状况进行了预警实证研究，结果发现：当赋予费米分布模型在财务预警领域的物理内涵后，一定程度上能够对输入的企业综合财务得分值E进行准确预测，其准确性主要决定于研究样本费米面EF的选择。EF越接近样本的实际值，则预警准确率会显著提高；同时，获得具有正、负相关性的E值对该模型的财务预警准确率至关重要。采用因子分析法和正、负相关性财务指标算术和的方法，分别对获取的E值輸入费米分布模型进行研究，表明采用因子分析法所得的E值由于考虑的企业财务指标过多过杂，对因子分析法所建模型和费米分布模型的预警准确率均产生了一定干扰。相比之下，采用正、负相关性财务指标算术和得到的E值能够有效提高费米分布模型的二进制预警准确率。

【关键词】 费米分布模型； 因子分析； 财务预警

【中图分类号】 F234.4 【文献标识码】 A 【文章编号】 1004-5937（2017）03-0044-05

一、引言

随着我国经济高速发展瓶颈的到来，经济活动进入新常态已成必然。从经济发展的类型看，以工业和农业为基础的国有经济逐渐趋于饱和，未来的发展逐步趋向服务性行业，包括交通输运、电子商务、房地产开发、新能源等，部分已经开始成为经济发展的新动力。与此同时，信息化程度的高度发展也使得服务性企业的竞争加剧，面临的机遇增多，一旦处理不当会给企业生存带来危机，如何使企业（特别是中小型企业）抵抗各种财务风险的能力显著提升，将会对其发展和决策起到至关重要的作用。基于此，为了能够全面合理地了解当前我国服务性行业上市公司的财务状况，并且能够为投资者提供科学的分析方法，本文选取了45家上市公司作为实证研究对象，其中包括2015年被ST的9家公司和与之以1：4配对的36家非ST公司。首次采用具有统计学原理的费米分布函数，建立了其在财务预警领域的新模型。本文选取的财务数据均来源于国泰安数据服务中心。

二、费米分布模型的建立

国内外学者[ 1-7 ]对财务预警的研究已经日益成熟，其中的研究方法大致分为单变量预警分析和多变量预警分析两类。最有影响的单变量分析模型是Fitzpatrick（1932）和William（1966）提出的。多变量分析模型已经成为当前研究的主流，应用比较广泛的包括：Altman（1968）提出的Z值模型，以及由此发展起来的F值模型和Y值模型等；Ohlson（1980）提出的Logistic线性回归模型；Coats和Fant（1993）提出的BP神经网络理论等。当前新的预警方法仍然层出不穷，但是无论哪种方法都有其优缺点和适用范围。为了能够对财务预警方面作出新的有益探索，本文引入具有统计学原理的费米分布函数来建立财务预警模型并对其进行实证研究。

费米分布函数是著名物理学家费米在研究半导体材料能级跃迁过程中的电子空穴分布状态时提出的。它是具有统计学原理的一种概率分布模型，由半导体物理[ 8 ]可知，当一个电子得到足够大的能量时，它就会从低能级向高能级跃迁，释放出能量时又会向低能级回落。费米分布描述的便是导带电子获得能量向价带跃迁的概率问题。基于此，可认为不同企业的财务状况是分布在不同的财务水平上的，财务预警机制便是通过提前对低财务水平的企业进行警示。当被警示后，企业可以通过注入新的有效能量来及时摆脱该状态，从而达到避免企业形势进一步恶化的目的。这也是财务预警研究的主要目的和目标，高的预测准确率一直都是财务预警的难点和主要出发点。

fn（E）=■ （1）

式（1）就是费米分布函数，下面将对其在财务预警领域各参数的物理内涵作解释，并赋值以建立费米分布模型。

（一）E是一个能够反映企业真实经济实力的参数，也可称之为企业的综合财务得分值

由文献可知，无论哪种财务预警模型都需要选取最能够代表企业财务状况的指标值，而该值的获取有很多方法，比如因子分析法、Z-score法、Y分数法、F分数法、比率法以及Logistic法等，本研究采用因子分析法和具有显著正、负相关性的财务指标算术和的方法分别获取E值。

（二）EF被称为费米面

其含义可理解为在某一财务预警的范畴内，衡量ST企业和非ST企业时的一个临界点。该值可从大样本数据的统计学中获得，其越接近样本实际情况则预测的准确率越高。而实际财务预警过程中，很难精确求得EF值，需要进行估算。在一定程度上，EF与实际样本数量及样本中所引入的ST企业数量呈正相关，另外还与样本整体E值的分布区间相关。因此，基于简化考虑，本研究对于该值采用如下定义：EF=（ST数/总样本数）*（样本E均值），当然也可以有多种其他合理定义，在此暂不予深入研究。

（三）k0T是衡量系统整体环境状态的相关量

任何企业都存在于一个大的经济环境条件下，而且这个环境随着时间的推移在发生变化。当系统经济发展水平越高时，分布在不同水平层次的企业数量将随之增加，表示竞争活力增强；当发展水平越低时，企业的分布层次将被压缩，只能向两个端面靠拢，表示竞争活力降低。考虑到实际企业所处的外部环境在短期内是不会发生非常明显变化的，正常情况下看作常数为宜。本研究对其赋予如下定义：k0T=1*0.072，其中k0为系统放大倍数，赋值为1，T定义为能够反映中国经济发展趋势的GDP增长率（2014年GDP增长率为7.2%），其他特殊情况暂不深入研究。

（四）fn（E）是企业被ST的概率值

如果其接近于1，则表示企业被ST的概率很大；如果接近于0，则表示被ST的概率很小。值得注意的是，由于公式中的k值为系统放大倍数，它的大小能够对输出概率值起到调节作用，本研究为了提高概率值的分辩率，赋值为1，所以一般情况下的预警概率近似二进制（即得到的概率值基本都是接近1或者0）。

三、因子分析法与费米分布模型实证研究

（一）因子分析法实证研究

通过文献调研借鉴以及指标选取所必需遵循的全面性、可比性、重要性及可操作性的原则，先从能够反映企业盈利能力、成长能力、偿债能力、现金流量能力、运营能力的240多项财务指标中选取了具有代表性的40个指标作为备选指标[ 9 ]。研究指标过多一方面不利于及时发现财务危机，另一方面指标之间若存在较大相关性可能会对分析结果产生偏差和误导。因此，在诸多财务预警文献中均对研究指标进行了显著性检验，主要检验方法包括参数检验和非参数检验。由于非参数检验统计方法不需要考虑研究对象的分布状态，所以研究以45家公司的40个备选指标为例，进行了两独立样本非参数U统计量的曼-惠特尼（Mann-Whitney）显著性检验。最终在显著性概率0.05水平上有16个指标通过，它们分别为：X1流动比率、X2速动比率、X3现金比率、X5现金流量净额/流动负债、X6资产负债率、X9权益对负债比率、X17资产报酬率、X18总资产净利润率、X19流动资产净利润率、X21长期资本收益率、X23营业成本率、X24营业净利率、X25成本费用利润率、X29资本积累率、X30总资产增长率、X37全部现金回收率。

由于因子分析法只适用于各变量之间相关性较大的情况，为了检验前述非参数检验所选取的财务指标是否可以用来做因子分析，继而进行了KMO和巴利特检验，结果显示KMO测试系数为0.774，近似卡方值为1 169.732，显著性值为0.000<0.05，表明所选取的16个财务指标间存在较强的相关性，非常适合进行因子分析。表1是采用正交旋转提取出的主成分因子的总方差解释，可以看出提取的5项主成分因子对原始数据信息解释达到91.22%。

利用表1中总方差解释的旋转载荷平方和的方差贡献率，可以得到样本的财务预警模型：

E = 0.30597*Z1 + 0.25228*Z2 + 0.17190*Z3 +

0.10544*Z4+0.07662*Z5 （2）

式（2）中Z1、Z2、Z3、Z4、Z5代表由16个企业各项财务指标所提取出来的5个主成分因子，分别表示盈利能力、成长能力、偿债能力、现金流量和运营能力。也就是说，预警模型最终是基于每个企业的这5项因子得分值与其权重的总和大小来作出预警判断。

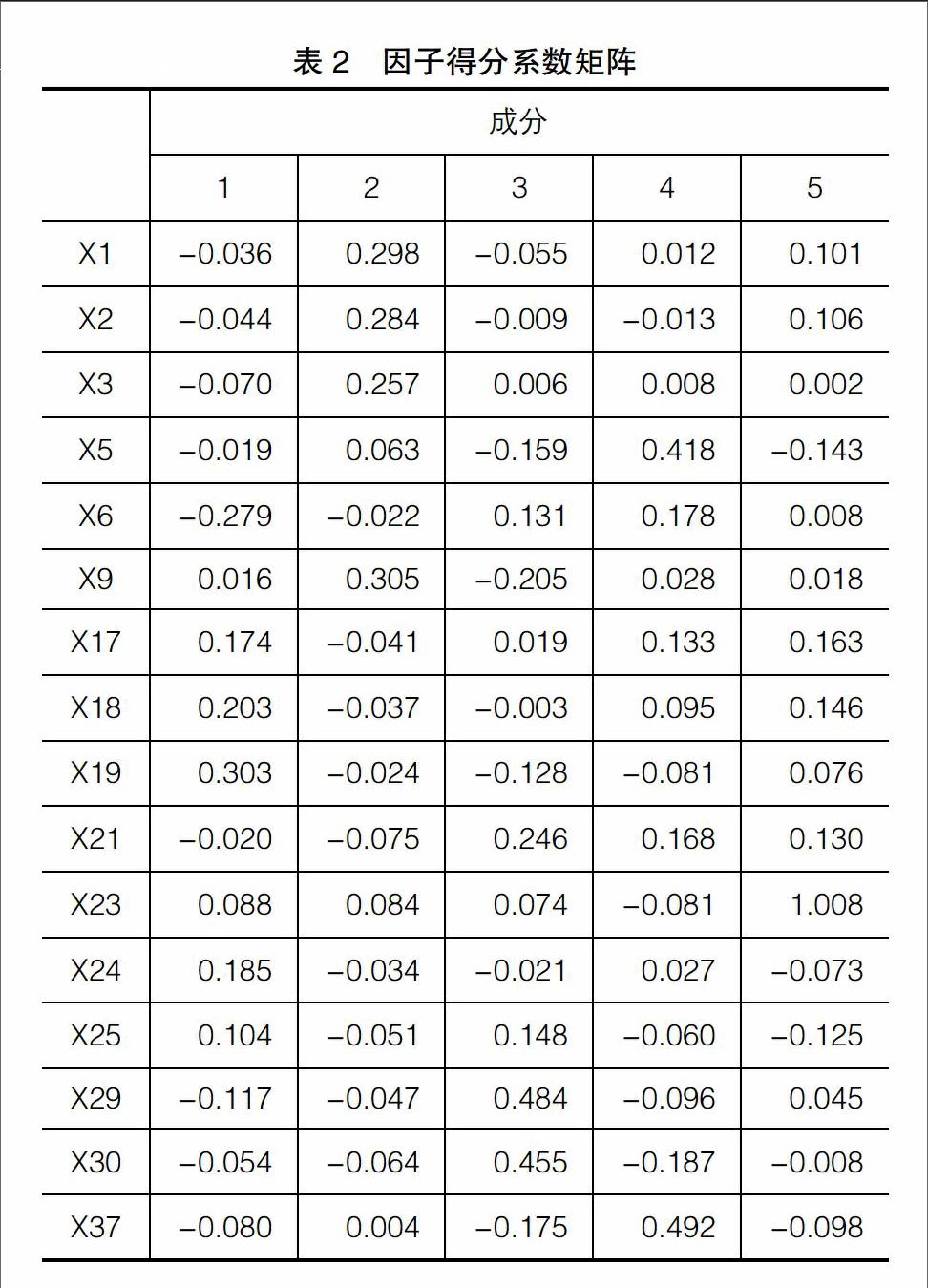
根据表2所列的因子得分系数矩阵可以计算出5项因子得分值，其与16个财务指标的线性表达式如下：

Z1=-0.036*X1 - 0.044*X2 - 0.070*X3 -0.019*X5-

0.279*X6 + 0.016*X9 + 0.174*X17 + 0.203*X18 +

0.303*X19 - 0.020*X21 + 0.088*X23 + 0.185*X24 +

0.104*X25-0.117*X29-0.054*X30-0.080*X37

Z2=0.298*X1 + 0.284*X2 + 0.257*X3 + 0.063*X5 -

0.022*X6 + 0.305*X9 - 0.041*X17 - 0.037*X18 -

0.024*X19 - 0.075*X21 + 0.084*X23 - 0.034*X24 -

0.051*X25-0.047*X29-0.064*X30+0.004*X37

Z3=-0.055*X1 - 0.009*X2 + 0.006*X3 - 0.159*X5 +

0.131*X6 - 0.205*X9 + 0.019*X17 - 0.003*X18 -

0.128*X19 + 0.246*X21 + 0.074*X23 - 0.021*X24 +

0.148*X25+0.484*X29+0.455*X30-0.175*X37

Z4=0.012*X1 - 0.013*X2 + 0.008*X3 + 0.418*X5 +

0.178*X6 + 0.028*X9 + 0.133*X17 + 0.095*X18 -

0.081*X19 + 0.168*X21 - 0.081*X23 + 0.027*X24 -

0.060*X25-0.096*X29-0.187*X30+0.492*X37

Z5=0.101*X1 + 0.106*X2 + 0.002*X3 - 0.143*X5 +

0.008*X6 + 0.018*X9 + 0.163*X17 + 0.146*X18 +

0.076*X19 + 0.130*X21 + 1.008*X23 - 0.073*X24 -

0.125*X25+0.045*X29-0.008*X30-0.098*X37

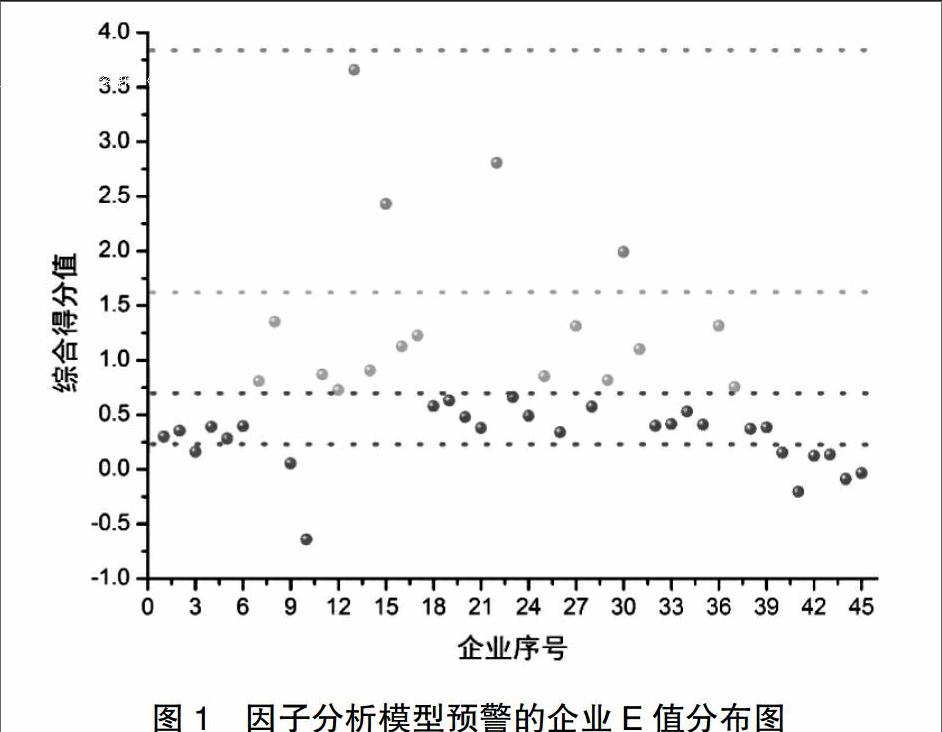
为了检验因子分析所建模型的准确性，将样本企业财务指标数据代入公式（2）进行计算并最终按照大小排序判别确定ST与非ST企业。该模型的准确率主要依据判别分割点的选择。为了表述简洁，对45个企业样本进行了编号处理，将预警模型得到的数据与对应企业绘制在图1之中。可以看出，这些样本企业得分可近似地划分为四个区域，黑色区域表示该企业财务处于危机状态，灰色区域分布了较多的企业，虽然得分相对黑色区稍高，但是有部分企业已经十分接近危机状态的边缘，甚至与其交错。在这之上的浅灰色区域的企业财务状态良好，处于最高区域的仅有少数几家。由相关文献可知，基于因子分析法所作的财务预警，大部分都是选择已知样本中ST和非ST的分割点建立模型的，最后使用该模型对预测样本作出判別。但是，由图1可以看到，对于该实证样本，其ST和非ST企业之间的分割点并不显著，在黑色线附近聚集了相对较多的企业。定性分析可知，这一现象在一定程度上将对所建模型的预警准确率产生影响，通过相关文献也可以证实采用因子分析法较其他预警方法并不很高明。需要说明的是，虽然图1给出因子分析预警模型对实证样本只误判了两家，但这一方面是由于样本数量小，另一方面则由于建模样本中的ST企业已知，从而能够选择出最佳分割点的缘故。

客观来说，因子分析的优势是能够综合企业财务指标的各个方面，取其精华而最终作出判断，同时可由提取的各主成分因子来进一步深入解读企业的财务能力。但是，通过上述实证研究发现，由于其综合能力很强，当考虑的指标信息量过多过杂时，会对所建模型的区分度矮化，模型分割点难以界定，从而不利于预警准确率的提升。

（二）费米分布模型实证研究

如前所述，关于费米分布模型在财务预警方面的基本物理内涵已经明确，下面采用该模型对样本财务预警进行实证分析。

为了证明费米分布模型的预警能力，分别使用了两种不同的方法获取企业E值来进行对比分析。第一种采用具有正、负相关性的企业各财务指标的算术和为E值；第二种是基于因子分析法所获得的E值。

分析可知，费米分布模型的重要判断依据是如何获得能够真实反映企业财务综合实力的相关指标。通过对大量企业财务指标的综合分析和评价发现，虽然财务指标很多，但是这些指标大致可分为三类：第一类指标是对于企业财务危机评价起不到显著作用，即危机企业和正常企业的指标不可区分；第二类指标是与企业财务危机程度呈现显著正相关，即指标值越大，企业财务状况越好；第三类指标是与企业财务危机程度呈现显著负相关，即指标值越大，企业财务状况越差。

为了简化研究过程中指标选取的受干扰程度，对于第一类指标进行排除或者尽量避免选择。第一种获取E值的方法是通过对因子分析法所得的16个具有显著性指标进一步分析，最终获得了具有正、负相关的8个指标。它们分别是X6资产负债率（负相关）、X17资产报酬率（正相关）、X18总资产净利润率（正相关）、X19流动资产净利润率（正相关）、X21长期资本收益率（正相关）、X24营业净利率（正相关）、X25成本费用利润率（正相关）、X29资本积累率（正相关）。于是可得到能够代表企业综合实力的计算公式：

E=X6+X17+X18+X19+X21+X24+X25+X29 （3）

采用费米分布模型进行预警，还需要赋予模型中参数EF值。理论上来说，在一个封闭的系统中，如果能够得到真实的EF值则其预警准确率接近100%，但在实际情况下是无法获得的，只能通过已知样本数据来进行估计。作为定性研究，本文给出了一种估计方式：即EF=（ST数/总样本数）*（样本E均值）。于是得出第一种方法的EF=9/45（E均值）=0.091927，第二种方法的EF=9/45（E均值）=0.1426754。

最后，将公式（2）和公式（3）两种方法获得的已知样本E值分别输入费米分布模型公式（1）中进行计算，即可得到实证结果。

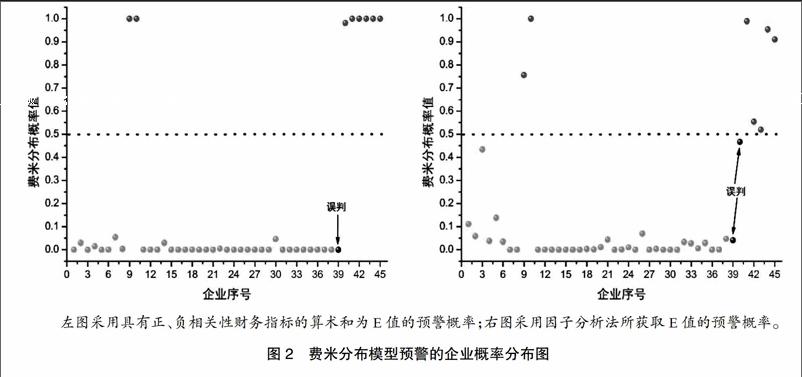
图2是两种E值的费米分布模型对已知样本的实证概率分布图。左图是采用6个具有正、负相关性财务指标的算术和得到的结果，45家企业误判的只有1家，而且预测出被ST的企业概率均接近1，而未被ST的企业概率均接近0。右图是采用因子分析获得的E值得到的结果，与前面的结果一致，有两家企业被误判。同时也可以看到另有3家（两家ST和1家非ST）企业的预测概率值接近于0.5，处于临界状态，交织状态明显。尽管如此，费米分布模型依然能够对其准确判断，这也说明其具有较高的分辩度。与此同时，这一结果同样证实了上面所述的问题：由于因子分析法考虑了过多过杂的综合财务信息，从而矮化了预警的灵敏性，表现出对于预警可靠性不高的事实。

整体而言，虽然采用了不同的方法来描述企业的综合实力，但都证实了从统计学中引入的费米分布模型是能够被应用于企业财务预警研究。可以推测，如果是基于大样本数据的统计结果，将会获得更接近于真实值的EF，其准确率有可能显著高于因子分析法的财务预警模型。另就预测结果而言，费米分布模型在相当程度上是二进制的，即1（代表被ST的概率）和0（代表非ST的概率）。这正是预警模型所需要的理想输出结果，同时该模型也可与其他预警模型协同，以弥补该模型未能提供的企业财务评价多元性分析。

四、结论

本文提出了一种基于统计学原理的费米分布模型来对企业财务预警进行了研究。

首先，该模型在一定程度上能够对输入的企业综合财务值E进行较准确的预警，其准确性主要决定于某一财务研究样本费米面EF的选择。当EF越接近于实际情况，其预警能力则会显著提高。

其次，对于费米分布模型而言，能够获得一种具有正、负相关性的企业综合财务值E对于财务预警的准确率至关重要。采用因子分析法所得到的E值，由于考虑的财务指标过多过杂，导致了无论是对因子分析预警模型还是费米分布模型的预警准确率产生干扰。相比之下，合理控制企业财务指标的数量，同时尽量选择具有正、负相关性的指标，可有效提高费米分布模型的二进制预警准确率。

最后，需要指出的是，对于引入费米分布模型到财务预警领域属于实证性研究，还需多方面的探索来完善。为了能够得到好的预警结果，仍有待进一步通过大量统计样本进行检验，并对模型中参数的财务内涵进行引申扩展。●

【参考文献】

[1] FITZPATRICK P J. A comparison of ratios of successful industrial enterprises with those of failed firms[M].New York：Certified Public Accountant，1932.

[2] BEAVER W H. Financal ratios as predictors of failures[J]. Journal of accounting research，1966（4）：71-111.

[3] ALTMAN E I.Financial ratios， discriminate analysis and prediction of corporate bankruptcy[J]. Journal of Finance，1968（9）：589-609.

[4] OHLSON J A. Financial ratios and the probabilistic prediction of bankruptcy[J]. Journal of Accounting Research，1980（1）：109-131.

[5] COATS P，FANT L F. Recognizing financial distress patterns using a neural network tool[J].Financial Management，1993（3）：142-155.

[6] 杨柳婷.基于因子分析法的采掘业上市公司財务绩效评价研究[J].经济研究参考，2014（5）：92-95.

[7] 孔宁宁，魏韶魏.基于主成分分析和Logistic回归方法的财务预警模型比较：来自我国制造业上市公司的经验证据[J].经济问题，2010（6）：112-116.

[8] 黄昆.固体物理学[M].北京：北京大学出版社，2009.

[9] 李建，宋丽平.指标选取对聚类分析的影响：以第三产业上市公司财务状况为例[J].财会月刊，2016（12）：84-87.