飞机等表速运动方程与稳态爬升参数计算

董新民, 陈勇

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

飞机等表速运动方程与稳态爬升参数计算

董新民, 陈勇

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

为了揭示等表速飞行的内在机理,建立了飞机等表速运动方程,提出了等表速爬升运动参数计算方法。对比等表速和等真空速爬升公式,提出了功率因子的概念,以反映飞机等表速与等真空速爬升所需单位剩余功率之间的关系。针对等表速等推力、等表速等梯度、等表速等升降速度3种典型爬升方式,应用飞机等表速运动方程给出了稳态运动参数计算方法。计算结果表明,3种爬升方式均存在稳态爬升剖面,稳态运动参数与表速呈一一对应关系。

飞机运动方程; 等表速; 功率因子; 稳态爬升剖面

0 引言

等表速爬升是飞机航线飞行中最常见的飞行动作[1-2]。等表速飞行能够确保飞机爬升升力不随高度变化,飞机姿态和轨迹易于控制,保证飞行安全。但目前飞机运动方程都是基于真空速建立的,给等表速运动的分析和计算带来了很大困难。国内外学者对飞机爬升性能及相关参数计算进行了深入研究[2-5]。美国空军飞行动力实验室总结了飞机起飞、爬升、巡航、转弯、下降和着陆等全飞行剖面运动参数的计算方法[6]。文献[7]建立了无人机巡航、爬升和下滑的轨迹优化模型。文献[8]以最短时间为指标,研究了大型军用运输机纵向飞行剖面的高度、速度和等效能量变化规律。文献[9-10]基于能耗最低、时间最短等指标研究了飞机爬升轨迹优化问题。但上述研究都是基于真空速展开的,其成果未拓展至等表速运动的参数计算。

本文建立了飞机等表速运动方程,并应用于等表速等推力、等表速等梯度和等表速等升降速度3种爬升方式,给出了稳态爬升参数计算方法。

1 基于表速的飞机质心运动方程

飞机纯纵向对称运动方程为:

(1)

式中:m为飞机质量;Vk为航迹速度;H为高度;G,D和L分别为飞机所受重力、阻力和升力;α和γ分别为飞机迎角和爬升角;T为发动机推力;σ为发动机安装角。通常σ≈0,则可得著名的能量公式为:

(2)

等式右边称为剩余功率。若剩余功率大于0,飞机保持高度则加速飞行,保持速度则爬升。必须指出,式(2)中Vk为航迹速度,在不考虑风时为真空速V。当飞机保持真空速不变时,等真空速爬升公式为:

(3)

但是,决定飞机气动力的不是真空速,而是表速。在实际飞行时,飞机大多是按表速飞行的。设表速为Vi,ρ0为标准海平面的大气密度,ρH为随高度变化的大气密度,则密度比υρ=ρH/ρ0,有[4]:

(4)

将式(4)求导并代入式(1),得到基于表速的飞机质心运动方程组为:

(5)

2 飞机等表速运动方程

在等表速飞行模态的任意时刻,Vi=Vi0为恒定的常值表速,可得飞机等表速运动方程为:

(6)

定义高度与表速的非线性函数为:

(7)

代入式(6)可得飞机等表速爬升公式为:

(8)

对比式(8)和式(3)可以看出,飞机等表速爬升的单位剩余功率比等真空速多了一项系数f(H,Vi0)。定义f(H,Vi0)为功率因子。显然,功率因子表示等表速爬升与等真空速爬升所需单位剩余功率的比值,为无量纲量。如果大气密度不随飞行高度变化,则f(H,Vi0)=1,两种爬升方式所需的能量相同。但实际飞行过程中,大气密度随高度不断变化,f(H,Vi0)≠1。因此,功率因子的存在说明,由于大气密度的变化,造成飞机等表速与等真空速爬升时所需的能量不同,这正是其物理意义所在。

3 等表速爬升运动参数计算

飞机主要有等表速等推力、等表速等梯度和等表速等升降速度3种典型爬升方式,下面分别讨论各爬升方式的运动参数计算方法。

3.1 等表速等推力爬升

飞机在等表速等推力爬升时满足Vi=Vi0,T=Tc,且均为常数。由式(6)和式(8)可得飞机等表速运动受力平衡方程为:

(9)

(10)

等表速下,马赫数随高度变化的关系式为:

式中:c为随高度变化的声速。升阻比与迎角α和Ma有关,等表速下Ma只与高度有关。令升阻比为K(α,H),从而有:

(11)

将式(10)和式(11)代入式(9),得到飞机的爬升角随高度变化的关系式为:

(12)

因为表速Vi=Vi0、爬升推力T=Tc均为常数,则式(9)和式(12)耦合后隐含变量α和H,可以采用数值法求出γ(H)及α(H)。若升力保持平衡,则等表速爬升剖面中稳态参数的计算步骤如下:

(1)对于任意高度H,若CLα为升力随迎角的变化率,Sw为机翼参考面积,α0为零升迎角,则根据以下力平衡方程组可求出稳态爬升迎角α;

(13)

(14)

(2)根据稳态爬升迎角α(H)计算不同高度下的升力L(α)、阻力D(α)和升阻比K(α,H);

(3)计算功率因子f(H,Vi0),由式(12)得到飞机等表速等推力爬升剖面的稳态爬升角γ(H);

(4)计算飞机俯仰角θ(H)=α(H)+γ(H)。

在定表速和定推力的前提下,存在一个稳态的爬升剖面,表速与迎角、爬升角、俯仰角等稳态运动参数之间存在一一对应关系。

3.2 等表速等梯度爬升

飞机在等表速等梯度(即爬升角)爬升时满足Vi=Vi0,γ=γc且为常数。通常,稳态爬升迎角α很小,根据式(9)可知爬升方式满足:

(15)

进一步结合式(14),求得迎角α为常值,且当给定爬升角γc不变时,存在对应的迎角α和俯仰角θ亦为常值。由式(11)得:

(16)

从而可知飞机在等表速直线平飞时,阻力为常值。结合式(10)得飞机推重比随高度变化的关系为:

(17)

可以看出,在飞机等表速等梯度直线飞行时,推力与表速之间存在稳态关系。爬升过程中需通过调节推力来稳定表速。

因表速Vi=Vi0、爬升角γ=γc均为常数,则式(17)耦合隐含变量α和H,可以采用数值法求解稳态参数。保持升力平衡,计算步骤如下:

(1)在任意高度H,由式(14)和式(15)组成升力平衡方程组,求出稳态爬升迎角α(H);

(2)计算不同高度下的升力、阻力和升阻比;

(3)计算功率因子f(H,Vi0),由式(17)得到等表速等梯度爬升剖面的稳态推力T(H);

(4)根据式(8)计算飞机稳态升降速度Vy(H)。

在定表速和定梯度的前提下,存在一个稳态的爬升剖面,爬升梯度与迎角、俯仰角等稳态运动参数之间存在一一对应关系。

3.3 等表速等升降速度爬升

飞机等表速等升降速度爬升时满足Vi=Vi0,Vy=Vy0为常值升降速度。结合式(1)得:

(18)

因此,爬升角随高度的变化规律为:

(19)

标准海平面对应的爬升角γ0=arcsin(Vy0/Vi0),即飞机等表速等升降速度爬升即表速不变、爬升角随高度变化的加速爬升过程。

对式(19)求高度的导数,可以得到:

(20)

通常,Vi0≫Vy0且ρ0≥ρH。由式(19)知,γ(H)较小,可认为处于线性范围内。则式(20)可简化为:

(21)

由于飞机稳态爬升时的迎角和爬升角均较小,可近似认为sinα≈0,cosγ(H)≈1。将式(19)和式(21)代入式(9)得:

(22)

结合式(10)和式(16),可以得到等表速等升降速度爬升方式下,飞机推重比随高度的变化规律为:

(23)

可以看出,飞机在等表速等升降速度爬升方式下,推力和表速之间存在稳态对应关系。爬升过程中需通过调节推力来稳定表速。

因表速Vi=Vi0、升降速度Vy=Vy0均为常数,则式(23)耦合隐含变量α和H,可采用数值法求解稳态参数。保持升力平衡,计算步骤如下:

(1)在任意高度H,结合式(14)和式(22)组成升力平衡方程组,求出稳态爬升迎角α(H);

(2)计算不同高度下的升力、阻力和升阻比;

(3)计算功率因子f(H,Vi0),由式(23)得到等表速等升降速度爬升剖面的稳态推力为T(H);

(4)根据式(8)计算飞机稳态爬升角γ(H)。

在定表速和定升降速度的前提下,存在一个稳态的爬升剖面,升降速度与迎角、爬升角、俯仰角等稳态运动参数之间存在一一对应关系。

4 计算结果及分析

4.1 等表速等推力爬升

以空客A-380飞机为例[11],重量为476 t,最大推力为4×311 169.6 N,稳定飞机推力5×105N,分别计算不同表速情形下等表速等推力爬升方式的稳态运动参数。图1所示为飞机稳态爬升角曲线,对应稳态爬升迎角如表1所示。

图1 稳态爬升角随高度变化曲线Fig.1 Curves of stable climb angle varying with height

Vi/kn260300340380α/(°)2.291.300.620.15

从图1可看出,飞机按等表速等推力爬升时,稳态爬升角随高度的增加逐渐减小,且飞机爬升至10 km高度时,稳态爬升角减小约1°。结合表1可知,稳态爬升角和稳态爬升迎角与表速对应,且随着表速的增大,稳态爬升角和迎角均逐渐减小。

4.2 等表速等梯度爬升

以空客A-380为例,给定爬升角γc=3°,计算等表速等梯度爬升方式的稳态运动参数。若飞机分别稳定在不同表速,结合式(15)和式(17)计算出的稳态爬升迎角如表2所示。图2为等表速等梯度爬升方式下飞机的稳态推力曲线,图3为相应的稳态升降速度曲线。

表2 不同表速时飞机的稳态爬升迎角

图2 稳态推力随高度变化曲线Fig.2 Curves of stable thrust varying with height

图3 稳态升降速度随高度变化曲线Fig.3 Curves of stable lifting velocity varying with height

由图2和图3可知,飞机在等表速等梯度爬升时,所需的推力随高度的增加逐渐增大;而稳态升降速度也在增加,即等表速等梯度爬升就是表速和爬升角不变的加速爬升过程。由图2可知,飞机表速越大,等梯度爬升需要的推力越大。

4.3 等表速等升降速度爬升

以空客A-380为例,给定升降速度Vy=15 m/s,计算等表速等升降速度爬升方式的稳态运动参数。若飞机分别稳定在不同表速,计算稳态爬升迎角,数值与表2一致。说明等表速等升降速度与等表速等梯度爬升时对应的稳态爬升迎角基本相同,进而可得到不同高度下保持升降速度爬升所需的推力,如图4所示。图5为相应的稳态爬升角曲线。

图4 稳态推力随高度变化曲线Fig.4 Curves of stable thrust varying with height

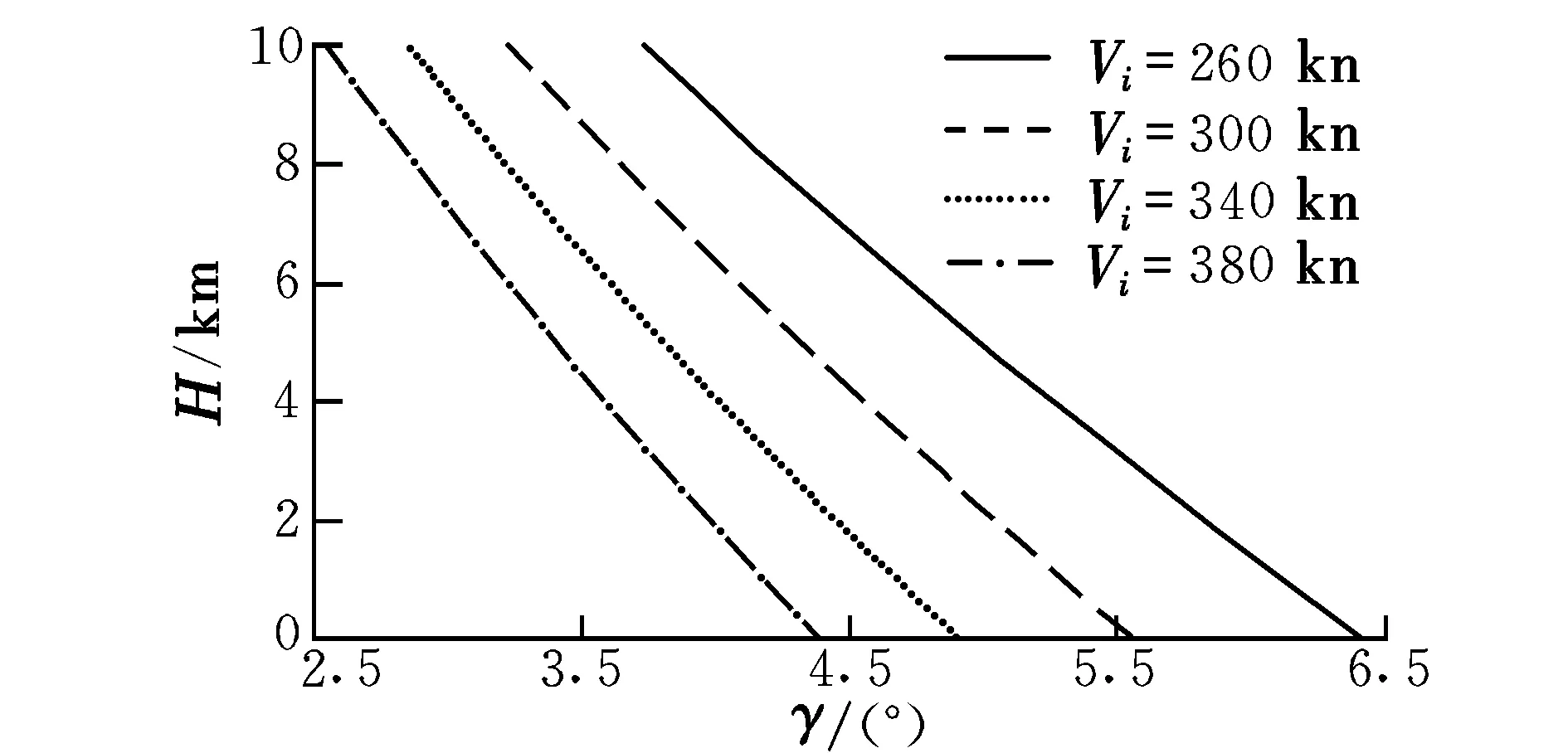
图5 稳态爬升角随高度变化曲线Fig.5 Curves of stable climb angle varying with height

在等表速等升降速度爬升方式下,飞机在不同表速时基本按恒定迎角爬升,以保证飞机等升降速度所需升力。由图4可知,推力随高度的增加逐渐降低,但与表速无明显变化规律。由图5可知,稳态爬升角随高度的增加逐渐降低,且相同高度下,表速越大,稳态爬升角越小。

5 结论

(1)飞机等表速爬升与等真空速爬升时所需的能量不同,其差异可用功率因子来描述;

(2)飞机在等表速爬升时,存在一个恒定的稳态爬升剖面,稳态运动参数在等表速等推力爬升时与表速和推力、在等表速等梯度爬升时与表速和爬升梯度、在等表速等升降速度爬升时与表速和升降速度均存在一一对应关系。

[1] 空中客车飞行运营支援及航线协助部.掌握飞机性能[M].图卢兹:空中客车公司,2002.

[2] 刘雪涛,张序.空客A320系列爬升性能研究[J].沈阳航空航天大学学报,2005,32(2):91-96.

[3] Timothy T T.Optimal climb trajectories through explicit simulation[R].AIAA-2015-2701,2015.

[4] 陈治怀,谷润平,刘俊杰.飞机性能工程[M].北京:兵器工业出版社,2006:26-28.

[5] 谷润平,李志超.飞机航路爬升与下降性能计算模型研究[J].中国民航飞行学院学报,2015,26(4):39-43.

[6] Air Force Flight Dynamics Laboratory.Aircraft flight performance methods[R].AFFDL-TR-75-89,1985.

[7] 陈晓,王新民,周健.无人飞行器纵向剖面轨迹优化[J].控制理论与应用,2013,30(1):31-36.

[8] 周堃,王立新.大型军用运输机的飞行航迹优化[J].北京航空航天大学学报,2010,36(6):654-658.

[9] 谷润平,刘芃.飞机航路爬升航迹的计算分析[J].中国民航大学学报,2003,21(4):13-15.

[10] 赵雷通,谢春生,张兆宁.航路爬升速度与爬升耗油函数模型研究[J].中国民航飞行学院学报,2014,25(6):5-8.

[11] 汇中.民用飞机设计参考机种之一:空客A380大型旅客机[J].民用飞机设计与研究,2010(3):25-28.

(编辑：李怡)

Aircraft equation of motion and stable climb parameters calculation with constant indicated airspeed

DONG Xin-min, CHEN Yong

(College of Aeronautics and Astronautics Engineering, AFEU, Xi’an 710038, China)

In order to find out the intrinsic truth about constant indicated airspeed (CIAS), the aircraft motion equation with CIAS was formulated and corresponding method to calculate the climb parameters was presented. Through comparing the climb formula between constant true airspeed (CTAS) and CIAS, the conception of power factor was proposed to reflect the relationship of the unit residual power required in climb between CIAS and CTAS. Three typical climb modes, such as CIAS and constant thrust, CIAS and constant climb gradient, CIAS and constant vertical speed, were discussed respectively. The methods to calculate the stable movement parameters were presented by applying the aircraft equation of motion with CIAS. Calculation results show that each mode has its stable climb section, stable movement parameters and CIAS present one-to-one correspondence.

aircraft equation of motion; constant indicated airspeed; power factor; stable climb section

2016-05-12;

2016-09-18;

时间:2016-11-10 09:10

国家自然科学基金资助(61304120；61473307)

董新民(1963-)，男，山东临沂人，教授，研究方向为飞行控制理论及应用； 陈勇(1984-)，男，四川中江人，讲师，研究方向为飞行控制理论及应用。

V212.1

A

1002-0853(2017)01-0011-05