基于高增益观测器的四旋翼无人机轨迹跟踪控制

王锐, 刘金琨

(北京航空航天大学 自动化科学与电气工程学院, 北京 100191)

基于高增益观测器的四旋翼无人机轨迹跟踪控制

王锐, 刘金琨

(北京航空航天大学 自动化科学与电气工程学院, 北京 100191)

为了实现四旋翼无人机对给定姿态的快速跟踪,基于Terminal滑模控制方法设计了一种四旋翼无人机的姿态控制器,在设计滑模面时引入非线性函数来保证跟踪误差在有限时间内收敛。考虑在线速度未知的情况下,通过设计高增益观测器来对无人机速度进行观测,并利用所观测的信号设计位置控制器。最后利用Lyapunov理论证明了系统的稳定性。仿真结果表明,四旋翼无人机在线速度不可测的情况下,仍可进行轨迹跟踪控制。

四旋翼无人机; 高增益观测器; Terminal滑模; 线速度反馈

0 引言

四旋翼无人机(Quadrotor UAV)具有结构简单、机动性强、安全可靠等优点,因此越来越多地被用来执行低空侦察、抢险救灾、航空摄影等任务[1]。四旋翼无人机具有4个控制输入和6个状态变量,是一个典型的欠驱动系统,这使得四旋翼无人机的控制问题具有一定的难度。许多文献研究了四旋翼无人机的控制问题,并提出了多种先进的控制算法,如滑模控制[2-3]、反馈线性化[4]、自适应控制[5]、模型预测控制[6]以及奇异摄动理论[7]等。文献[2]将四旋翼无人机的模型以状态空间的形式表示,采用内外环方法设计控制律,设计了滑模控制器。文献[5]利用内外环结构,对外回路设计了基于反步法的控制器,内回路引入了L1自适应控制对系统进行补偿。文献[6]设计了一种H∞控制器来追踪理想角度,基于模型预测控制理论设计了位置控制器。上述文献大多采用了内外环结构实现四旋翼无人机的控制器设计:先对四旋翼无人机的位置控制器进行设计,通过位置控制器得到理想姿态以及实际升力,最后设计姿态控制器来跟踪理想姿态。这就要求姿态控制器能够迅速跟踪姿态指令,因此,姿态控制器的性能决定了四旋翼无人机系统的整体性能。文献[7]利用奇异摄动理论,定量分析了内外环之间的增益关系,指出姿态收敛需要高的增益才能保证快速性,并给出了高增益参数的范围。

现有的大部分方法仅能够保证系统状态的渐进收敛。实际工程应用中,人们更需要系统在有限时间内收敛;然而在传统的滑模控制中,状态跟踪误差不会在有限时间内收敛到零。此外,无人机在低速飞行时,平动线速度可以根据GPS传感器的测量信号近似差分得到。但是,当四旋翼无人机位于室内或者桥梁下方,由于信号衰减或者阻塞,可能会导致GPS传感器失效。此时位置信号可以借助高度计和摄像头传感器得到,但是线性度不可测,平动线速度信息无法获得。为了获得更好的控制效果,本文考虑平动线速度不可测情况下的四旋翼无人机轨迹跟踪控制。

1 四旋翼无人机动力学模型

四旋翼无人机的结构如图1所示。

图1 四旋翼无人机结构图Fig.1 Structure diagram of quadrotor UAV

定义Ogxgygzg为惯性参考系,方向为北、东、地;Obxbybzb为本体坐标系,原点与无人机中心重合,满足右手定则。由于传统的欧拉角描述姿态会引起奇异现象,本文使用单位四元数描述无人机的姿态。定义单位四元数为Q=[qT,η]T∈R4,q=[q1,q2,q3]T∈R3为单位四元数矢量部分,η∈R为单位四元数标量部分,满足qTq+η2=1;R(Q)∈R3×3为从惯性坐标系到本体坐标系的旋转矩阵,可用四元数表示为[8]:

(1)

四旋翼无人机动力学微分方程为:

(2)

式中:m为无人机质量;g为重力加速度;I为惯性矩阵;T∈R为待设计的四旋翼无人机输入升力;MΣ为待设计的输入转矩,MΣ=[MΣ1,MΣ2,MΣ3]T∈R3。T,MΣ与旋翼转速fi(i=1,2,3,4)的关系为[9]:

(3)

式中:l为四旋翼本体坐标系原点到螺旋桨中心的距离;CD为阻力系数;CL为升力系数。

由式(3)可知,完成升力与转矩的设计后,即可唯一确定4个旋翼所需的转速。

2 姿态子系统控制器设计

(4)

其中:

从而可以建立模型(2)的姿态误差系统为:

(5)

其中:

选取滑模函数:

(6)

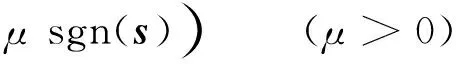
(7)

3 位置子系统高增益观测器及控制器

设计

3.1 高增益观测器设计及稳定性分析

(8)

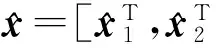
(9)

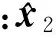
(10)

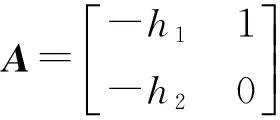
3.2 控制器设计

对于位置子系统,设计滑模函数为:

(11)

其中:

设计三维控制输入U=[u1,u2,u3]T为:

(12)

通过设计出的U可得到实际升力输入T为:

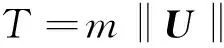
(13)

理想姿态以及理想角速度为:

(14)

(15)

4 稳定性分析

控制系统的稳定性可以总结为如下定理:

定理1:考虑式(2)描述的四旋翼无人机姿态子系统,对于式(14)和式(15)表示的参考信号Qd和Ωd,采用式(7)所设计的输入转矩M∑,可以使系统的状态变量q,η,Ω在有限时间内收敛到期望的轨迹。

(16)

因此有:

(17)

当s=0时,Terminal滑模面满足:

(18)

对式(18)分离变量,并对等号两端积分可得:

(19)

最终可以得到系统达到平衡状态的时间为:

(20)

定理2:考虑式(2)四旋翼无人机位置子系统,对于给定的参考信号Pd,采用式(12)和式(13)所设计的输入升力T和观测器(9),可以使闭环系统渐进稳定,且系统状态变量P,v收敛到期望轨迹。

(21)

(22)

其中:

(23)

5 仿真验证及结果分析

由图2可以看出,在线速度信号不可测时,状态高增益观测器可以仅通过位置信息实现对无人机速度的快速估计;由图3可知,利用所观测的速度信息设计的位置控制器可以保证系统对目标轨迹的跟踪;由图4可以看出,所设计的Terminal滑模控制器可以实现对目标姿态的快速跟踪。

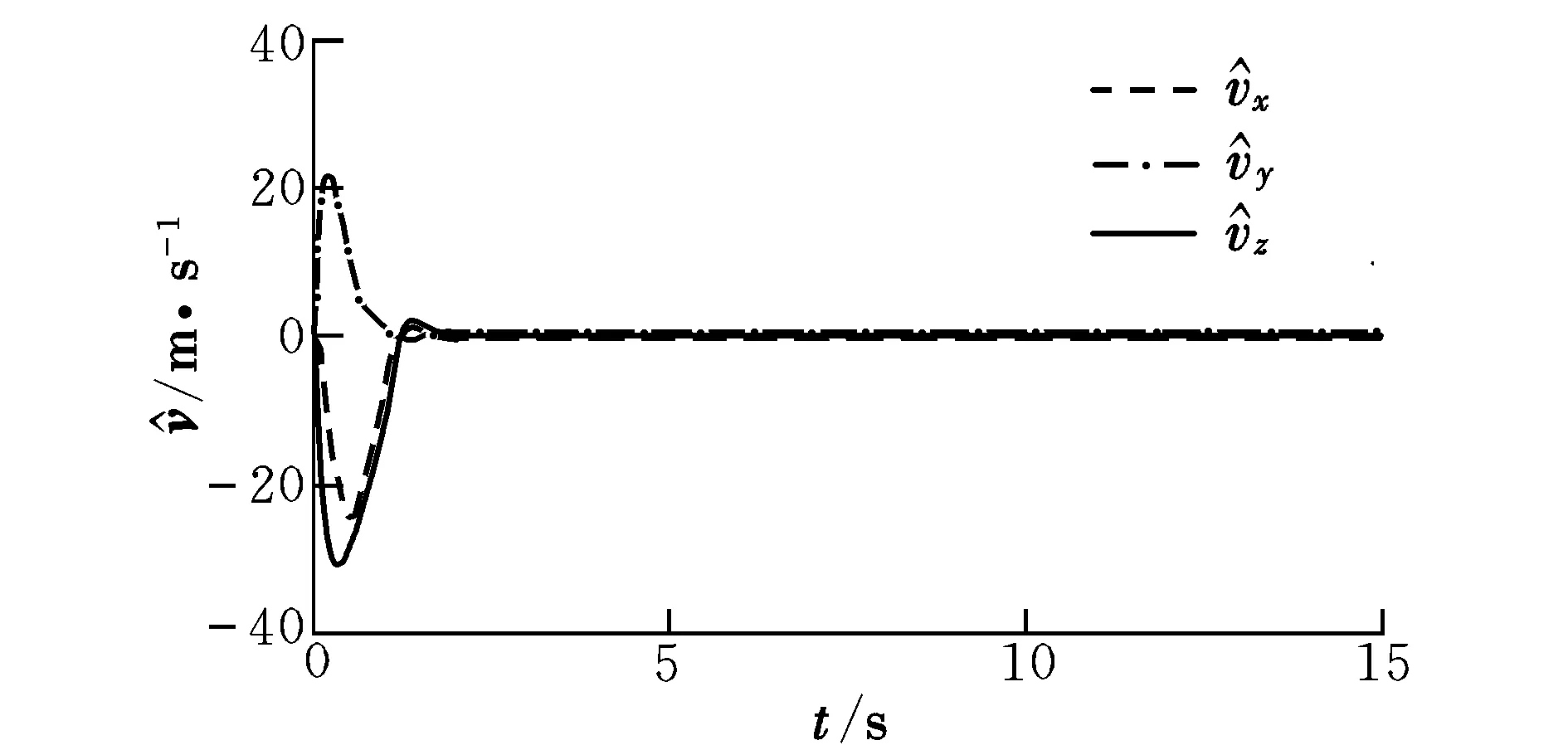
图2 速度观测误差Fig.2 Velocity estimate errors

图3 轨迹跟踪误差Fig.3 Trajectory tracking errors

图4 姿态跟踪误差Fig.4 Attitude tracking errors

6 结束语

为了实现四旋翼无人机姿态的快速跟踪,首先通过引入Terminal滑模面,设计出了在有限时间内收敛的姿态控制器;其次考虑在平动线速度不可测、仅知道位置信号的情况下,设计指数收敛的高增益观测器估计出速度信号;最后利用内外环结构,设计出了位置控制器。仿真效果表明,高增益观测器可以快速观测出实际的速度信息,所设计的控制器在平动线速度不可测的情况下,仍然可以实现对四旋翼无人机参考轨迹的快速跟踪。

[1] Yang L,Liu J.Parameter identification for a quadrotor helicopter using PSO[C]//Decision and Control (CDC),2013 IEEE 52nd Annual Conference on.Florence,Italy:IEEE,2013:5828-5833.

[2] 方旭,刘金琨.四旋翼无人机三维航迹规划及跟踪控制[J].控制理论与应用,2015,32(8):1120-1128.

[3] Besnard L,Shtessel Y B,Landrum B.Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer[J].Journal of the Franklin Institute,2012,349(2):658-684.

[4] Lee D,Kim H J,Sastry S.Feedback linearization vs.adaptive sliding mode control for a quadrotor helicopter[J].International Journal of Control,Automation and Systems,2009,7(3):419-428.

[5] 甄红涛,齐晓慧,李杰,等.四旋翼无人机L1自适应块控反步姿态控制器设计[J].控制与决策,2014,29(6):1076-1082.

[6] Raffo G V,Ortega M G,Rubio F R.An integral predictive/nonlinearH∞control structure for a quadrotor helicopter[J].Automatica,2010,46(1):29-39.

[7] Bertrand S,Guénard N,Hamel T,et al.A hierarchical controller for miniature VTOL UAVs:design and stability analysis using singular perturbation theory[J].Control Engineering Practice,2011, 19(10):1099-1108.

[8] Shuster M D.A survey of attitude representations[J].Journal of the Astronautical Sciences,1993,41(4):439-517.

[9] Zuo Z.Trajectory tracking control design with command-filtered compensation for a quadrotor[J].IET Control Theory & Applications,2010,419(11):2343-2355.

[10] Khalil H K,Praly L.High-gain observers in nonlinear feedback control[J].International Journal of Robust & Nonlinear Control,2007,24(6):249-268.

[11] Krstic M,Kanellakopoulos I,Kokotovic P.Nonlinear and adaptive control design[M].New York:Wiley Interscience,1995:74-75.

(编辑：李怡)

Trajectory tracking control of quadrotor UAV based on high-gain observer

WANG Rui, LIU Jin-kun

(School of Automation Science and Electrical Engineering, BUAA, Beijing 100191, China)

An attitude controller for quadrotor UAV was designed based on terminal sliding mode control method to ensure a rapid orientation tracking, where a nonlinear function was introduced to design a terminal sliding mode surface, so that the tracking error could converge to zero in finite time. Considering the linear velocity was unavailable for feedback, a high-gain observer was designed to estimate the linear velocity of the quadrotor UAV. With the estimate value of the linear velocity, a position controller was designed. Based on Lyapunov theory, the stability of the closed-loop system was proved. Simulation results show that a rapid trajectory tracking performance is guaranteed without linear velocity feedback.

quadrotor UAV; high-gain observer; Terminal sliding mode; linear velocity-free feedback

2016-06-16;

2016-10-25;

时间:2016-11-10 09:10

国家自然科学基金资助(61374048)

王锐(1992-)，男，山东烟台人，硕士研究生，研究方向为无人机飞行控制； 刘金琨(1965-)，男，辽宁大连人，教授，博士生导师，研究方向为先进运动控制。

V249.1

A

1002-0853(2017)01-0039-04