升力体式密闭救生舱无控制再入研究

王禹, 张劲柏, 洪娟, 徐航, 兰世隆

(1.北京航空航天大学 国家计算流体力学实验室, 北京 100191;2.中航工业航宇救生装备有限公司, 湖北 襄阳 441003)

升力体式密闭救生舱无控制再入研究

王禹1, 张劲柏1, 洪娟2, 徐航2, 兰世隆1

(1.北京航空航天大学 国家计算流体力学实验室, 北京 100191;2.中航工业航宇救生装备有限公司, 湖北 襄阳 441003)

将救生舱选定为升力体模型,利用数值模拟的方法动态研究救生舱再入过程中的稳定性和减速性,分析无主动控制的救生舱返回的可行性。针对高超声速和马赫数小于4两种工况,分别采用牛顿理论方法和CFD方法进行气动力计算;利用气动特性计算结果求解六自由度轨道仿真动力学方程进行轨迹计算。研究结果显示,救生舱初始再入条件合适时,其再入过程具有稳定性;仅依靠目前救生舱外形的结构减速不能满足减速性要求,需辅助其他减速措施。

救生舱; 高超声速; 稳定性; 减速性; 数值计算

0 引言

密闭救生舱是目前已知的唯一能可靠实现载人航天器“全轨道”安全救生的技术措施[1]。与传统敞开式弹射救生相比,最主要的优点是可适用的救生包线宽、乘员的高速防护性能优良、乘员落地或入水后的生存条件较好。在人类载人航天的发展过程中出现5次一等事故,共21名航天员遇难,其严重事故发生的概率超过了传统的军用作战飞机[2]。随着我国对高超声速飞机、空天飞机等新一代飞行器的研究已取得实质性进展,对救生舱这种救生模式的关注程度也逐渐提高。救生舱与返回舱不同,主要是其要求总体结构要尽量简单,但又具有较高的可靠性;因此，提出无动力无控制密闭救生舱升力体模型的概念。

在航天器以宇宙速度再入地球大气环境的飞行过程中,对航天器气动性能的要求主要包括减速飞行、控制轨迹、稳定飞行及气动加热[3]。本文从稳定性、减速性及再入轨迹特性出发,分析无动力、无控制密闭救生舱再入的可行性:首先,以“快船号”飞行器为救生舱原型机重构其三维模型,并针对救生舱任务对原型机模型进行修改;其次,分别利用工程估算法和Fluent计算平台进行救生舱气动特性的计算;最后,数值模拟救生舱再入过程,评估其稳定性和减速性。

1 救生舱模型及网格

1.1 救生舱模型

以无翼升力体式“快船号”飞行器为原型机进行建模。在原型机的基础上,基于反设计近似,将已知几何构型横截面划分为上表面、中间过渡曲面和下表面3个形状控制线。基于圆锥曲线拼接的思想将控制线封闭为统一的非轴对称参数化截面形状。通过动态调整少量的形状参数,可获得轮廓曲面,实现类“快船号”救生舱建模。“快船号”的详细几何尺寸见文献[4],对其头部进行修改,得到救生舱几何模型如图1所示。

图1 密闭救生舱几何模型Fig.1 Geometric model of closed-type rescue capsule

救生舱模型轨迹计算参数为:总质量为8 t;重心坐标为(3.6,0,-0.157)m;转动惯量矩阵为Iox=9 491 kg·m2,Ioy=21 568 kg·m2,Ioz=22 478 kg·m2,Ixy=-15.4 kg·m2,Iyz=0.461 kg·m2。

1.2 计算网格

计算中采用结构化六面体网格,网格总数约400万。为保证计算的准确性,在模型的近壁区和机头前部的网格均进行了加密处理,第一层网格离壁面的距离为1 mm。救生舱结构网格如图2所示。

图2 救生舱结构网格Fig.2 Structured grids of rescue capsule

2 计算方法

2.1 气动特性计算

为提高计算效率,在计算气动力、力矩时采用气动工程算法和CFD方法。气动工程算法计算速度快,计算耗费少[5]。大部分针对高超声速气动力的研究都使用了牛顿理论[6]、激波膨胀波理论以及活塞理论。气动工程算法假设高超声速气流无粘性并忽略真实气体效应,却可以提供足够精确的结果[7-8]。本文采用牛顿理论方法计算Ma>4工况下的气动力和力矩。

CFD方法直接求解N-S方程,得到的气动力计算结果精度较高,但计算耗时长。在较低马赫数工况(Ma<4)计算中可借助Fluent计算平台进行。Fluent计算时选取三种边界条件:将救生舱表面选为wall壁面边界条件,设定壁面参数;将Y=0平面选为symmetry对称面边界条件,以节省计算资源;设定外部流场的外边界为pressure-far-field压力远场边界条件,并针对不同工况将不同高度下的总温、静压、马赫数和来流方向等参数依据标准大气表进行设定。此外,在计算时设定密度基求解器Density Based、隐式求解方法Implicit、定常流动Steady,同时开启能量方程,选定湍流模型k-ω(2eqn)SST模型。

图3给出了Ma=5,H=30 km工况下,使用牛顿理论算法和Fluent软件计算气动特性的结果。

由图3可以看出,采用牛顿理论计算气动力的结果和Fluent的计算结果基本一致,误差很小。证明了气动工程算法程序的可靠性,以及Fluent计算边界条件设定的合理性。

2.2 轨迹计算

本文轨迹计算是求解六自由度轨道仿真动力学方程[9]。航天器返回时的六自由度轨道仿真动力学方程由质心动力学方程和绕质心动力学方程两部分组成,包含12个独立的微分方程和若干辅助计算方程。辅助计算方程主要包括坐标变换、绝对速度计算、过载计算等方程。具体算法、坐标系说明及方程的求解见文献[10-12],本文不再赘述。

3 数值计算及结果分析

3.1 计算工况

选取3组航天器典型再入初始条件对本文救生舱模型进行再入仿真计算,再入初始条件为:工况1:H=300 km,V=7.72 km/s,γ=-1°;工况2:H=300 km,V=7.72 km/s,γ=-1°,-2°,-3°;工况3:H=120 km,V=7.83 km/s,γ=-1°,-2°,-3°;工况4:H=30 km,Ma=4,γ=-1°,-2°,-3°。

3.2 稳定性计算

3.2.1 稳定性分析方法

飞行器再入过程中,航天器动态气动性能是保证航天器稳定飞行的关键。航天器以稳定的配平迎角减速下降,需满足如下条件:

本文主要考虑救生舱的静稳定性,根据救生舱再入过程迎角的变化情况分析其稳定性。若救生舱再入过程中发生翻转,则认为其不具备稳定性;而若救生舱始终在某一迎角值附近振荡,则进一步根据角速度的大小,判断其稳定性。

3.2.2 不同再入初始条件下稳定性分析

(1)在工况1条件下,救生舱的飞行轨迹特性如图4所示。

图4 工况1条件下的轨迹特性Fig.4 Trajectory characteristics for working condition 1

由图4可以看出,救生舱的飞行高度、迎角及爬升角均作周期性变化,周期约为5 700 s,救生舱在该初始条件下绕地球作椭圆轨道运动,未返回。

(2)在工况2条件下,救生舱的稳定性计算结果如图5所示。

图5 工况2条件下的稳定性Fig.5 Stability for working condition 2

由图5可以看出,救生舱在该工况下为返回过程:救生舱开始运动时迎角逐渐增加,从0°增加到40°以上;迎角达到最大值时纵向俯仰力矩变为低头力矩,迎角开始减小;但当迎角小于40°以后,纵向俯仰力矩又变为抬头力矩,迎角开始增加。此后救生舱将一直在迎角40°附近振荡且迎角值略有增加,同时振荡幅度越来越小。俯仰角速度最大值为0.06 rad/s,满足救生舱稳定性设计要求。

(3)在工况3条件下,救生舱的稳定性计算结果如图6所示。

图6 工况3条件下的稳定性Fig.6 Stability for working condition 3

与前面工况的计算结果一致,救生舱返回时迎角值在40°附近振荡,且振荡幅度减小,40°为其稳定迎角值。俯仰角速度最大值为0.25 rad/s,与上一工况相比略有增大。

(4)在工况4条件下以不同再入角返回时,首先计算初始迎角为0°的情况。计算结果显示救生舱迅速失稳、翻转。由前面计算结果可知，救生舱具有40°稳定迎角,因此考虑设定初始迎角为40°。在工况4和初始迎角40°条件下的稳定性计算结果如图7所示。

图7 工况4和初始迎角为40°条件下的稳定性Fig.7 Stability for working condition 4 and α0=40°

由图7可以看出,救生舱在减速至亚声速前,其迎角在40°附近振荡,同时其俯仰角速度值最大为0.1 rad/s,具有稳定性。但在亚声速时,救生舱迅速失稳、翻转。飞行器在超声速时压心位置靠后,具有一定稳定性,而减速至亚声速时,压心位置迅速前移并失稳。因此,亚声速时需辅助稳定伞等方法保证其稳定性。

3.3 减速性计算

3.3.1 减速性分析方法

分析救生舱减速性时考虑两方面情况:第一,救生舱减速所用时间及返回至特定高度时能否减速至相应速度。可参考两个减速性能指标:高度降低至30 km,速度减至Ma=4;高度降低至10 km,速度减至亚声速。第二,救生舱再入过程中过载的变化情况。

3.3.2 不同再入初始条件下的减速性

(1)在工况2条件下,救生舱的减速性如图8所示。

图8 工况2条件下的减速性Fig.8 Deceleration for working condition 2

由图8可以看出,救生舱高度下降至30 km,速度减至约1.2 km/s(Ma≈4)。再入角越大,救生舱再入时间越短,减速效应越明显。再入角为-3°时,其过载最大值接近12。救生舱在40～70 km高度减速最明显,在该高度下大气密度增大,救生舱所受气动力作用明显。在该段内过载值偏大,一方面可通过救生舱外形的设计,提高升阻比,优化再入轨迹特性;另一方面可以采用辅助减速措施,提高其减速性能。

(2)在工况3条件下,救生舱的减速性如图9所示。

图9 工况3条件下的减速性Fig.9 Deceleration for working condition 3

由图9可以看出,救生舱减速至25 km高度时,速度可以减至Ma≈4。同样地,再入角越大,救生舱再入时间越短。救生舱再入过程中过载最大值达到13。

(3)在工况4和初始迎角为40°条件下,救生舱的减速性如图10所示。

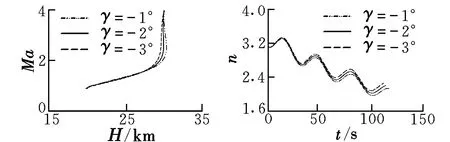
图10 工况4和初始迎角40°条件下的减速性Fig.10 Deceleration for working condition 4 and α0=40°

由图10可以看出,救生舱减速至亚声速时,对应高度约为18 km;在工况4初始条件下返回时,再入角对救生舱的返回时间几乎没有影响;此工况下,救生舱过载最大值约为3.4。

4 结束语

本文针对可用于邻近轨道空天飞机高超声速环境下的密闭救生舱进行探索性研究,利用数值模拟方法计算救生舱模型高超声速下的稳定性和减速性,分析升力体模型的密闭救生舱无动力再入的可行性。从计算结果看:一方面从稳定性方面考虑,现阶段计算的救生舱模型在超声速的范围内具有一定的稳定性,但要求其再入初始条件合适;在亚声速时,救生舱不具备稳定性,可采用稳定伞等方式保证其稳定性。另一方面从减速性考虑,救生舱的减速效率满足要求,但其在减速过程中可能面临过载过大的问题,需在下一步工作中通过外形的优化或者利用辅助减速措施进一步提升减速性能。综合考虑,认为密闭救生舱无主动控制再入返回的设计思路具有一定可行性,但前提必须在进一步的详细设计中解决上述问题。

[1] 王祥甫,姜楠.载人飞行器应急救生技术发展研究[C]//2008-2009航空科学技术发展报告.2009:96-106.

[2] 王向阳.国外载人航天器的应急救生[J].中国航天,1993(8):36-40.

[3] 方方,周璐,李志辉.航天器返回地球的气动特性综述[J].航空学报,2015,36(1):24-38.

[4] 赵彪,崔乃刚,郭继峰,等.快船式飞行器参数化建模及高超声速气动计算[J].宇航学报,2013,34(8):1040-1046.

[5] 杨超,谢赟,谢长川.高超声速飞行器气动弹性力学研究综述[J].航空学报,2010,31(1):1-11.

[6] 霍霖.复杂外形高超声速飞行器气动热快速工程估算及热响应分析[D].长沙:国防科学技术大学,2012.

[7] Hanson P W.Aerodynamic effects of some configuration variables on the aero-elastic characteristics of lifting surfaces at Mach numbers from 0.7 to 6.86[R].NASA-TN-D-984,1961.

[8] McNamara J.Aero-elastic and aero-thermo-elastic behavior of two and three dimensional surface in hypersonic flow[D].Michigan: University of Michigan-Ann Arbor,2005.

[9] 何争.载人飞船自主应急返回动力学与控制研究[D].长沙:国防科学技术大学,2009.

[10] 赵汉元.载人飞船再入轨道和制导规律设计及六自由度弹道仿真[J].航天返回与遥感,2001,22(1):38-42.

[11] 汤国建,赵汉元.载人飞船返回舱六自由度再入弹道仿真研究[J].飞行力学,2000,18(3):80-84.

[12] 白东升.载人飞船应急返回轨迹规划设计[D].北京:北京航空航天大学,2000.

(编辑：李怡)

Researches on non-control reentry for lifting-type rescue capsule

WANG Yu1, ZHANG Jin-bai1, HONG Juan2, XU Hang2, LAN Shi-long1

(1.National Laboratory for Computational Fluid Dynamics, BUAA, Beijing 100191, China;2.AVIC Aerospace Life-support Industries Ltd., Xiangyang 441003, China)

Lifting body model was used for rescue capsule. Stability and deceleration of rescue capsule during reentry process were studied dynamically with numerical simulation, and the feasibility of non-control rescue capsule’s reentry was analyzed. For the conditions of hypersonic andMa<4, the aerodynamic calculations were proceeded respectively with Newton theory and CFD method. With the results of aerodynamics characteristics, the trajectories were computed by solving six degree of freedom trajectory simulation dynamics equations. Study results show that rescue capsule has stability if its reentry initial conditions are appropriate. In addition, the deceleration only by its’ structure can not meet design requirements, it needs to be assisted by other deceleration measures.

rescue capsule; hypersonic; stability; deceleration; numerical calculation

2016-07-06;

2016-10-09;

时间:2016-11-10 09:10

航空科学基金资助(20140091555431)

王禹(1991-)，男，辽宁沈阳人，硕士研究生，研究方向为计算流体力学。

V411.8; V412.4

A

1002-0853(2017)01-0021-04