基于滑模控制的四旋翼无人机自适应跟踪控制
2017-02-15刘凯悦冷建伟
刘凯悦, 冷建伟
(1.天津理工大学 自动化学院, 天津 300384;2.天津市复杂系统控制理论及应用重点实验室, 天津 300384)
基于滑模控制的四旋翼无人机自适应跟踪控制
刘凯悦1, 冷建伟2
(1.天津理工大学 自动化学院, 天津 300384;2.天津市复杂系统控制理论及应用重点实验室, 天津 300384)
针对四旋翼无人机在系统内部模型参数不确定性情况下的轨迹跟踪问题,提出了一种基于滑模控制的四旋翼无人机自适应跟踪控制方法。首先,采用单位四元数来描述系统姿态,将系统分解为位置子系统和姿态子系统;考虑到位置子系统的欠驱动特性,引入了虚拟控制力,跟踪位置信息并解算出实际升力和理想姿态;其次,通过自适应滑模控制器补偿了质量和转动惯量的不确定性,实现了轨迹的跟踪;最后,利用Lyapunov理论证明了闭环系统的稳定性。仿真结果表明了算法的有效性。
四旋翼无人机; 单位四元数; 虚拟控制力; 自适应滑模控制
0 引言
与传统的直升机相比,四旋翼无人机的工艺更简单、安全性能更强、飞行效率也更高,因此在军事和民用领域的应用越来越广泛,例如监控、侦察、在恶劣环境下的探索和救援任务等[1]。然而其固有的非线性、欠驱动、强耦合性以及系统参数未知等特性,使得四旋翼无人机系统的控制器设计仍然是一项具有挑战性的任务[2-3]。
目前,在系统模型参数存在不确定性的前提下,为了实现四旋翼无人机轨迹跟踪的目标,已提出了多种控制器设计方案。文献[4]设计了模糊自适应控制器,有效地补偿了系统未建模参数的摄动和外界干扰。王焱等[5]采用鲁棒滑模控制方法,实现了对期望值的有效跟踪。甄红涛等[6]设计了一种鲁棒自适应反步控制器,抵消了不确定性对系统的影响,但采用欧拉角描述姿态会产生奇点,跟踪效果不佳。文献[7-9]在Lyapunov理论的基础上,采用自适应控制的方法,将位置子系统的跟踪误差收敛到0,保证了四旋翼无人机控制性能趋近于系统参数未改变时的控制性能。陈向坚等[10]提出了基于区间二型模糊神经网络的自适应控制器,通过在线逼近系统不确定性,证明了系统的闭环稳定性。
本文首先采用单位四元数法对姿态加以描述,同时考虑四旋翼无人机的欠驱动特性,将整个系统分解为位置和姿态两个子系统[11]。通过位置子系统中虚拟控制力的设计,可以得到实际输入升力和理想四元数,实现了位置子系统的指令跟踪。另外,针对四旋翼无人机的参数存在不确定性问题,采用自适应控制方法设计自适应律进行补偿,保证四旋翼无人机的轨迹跟踪。
1 系统数学模型
四旋翼无人机是由固定在一个十字框架结构上的两对互相旋转的螺旋桨组成,这种结构使得四旋翼无人机具有垂直起降、空中悬停和朝任意方向飞行等优点[12]。定义Obxbybzb为四旋翼无人机的本体坐标系;选取北、东、下坐标系作为无人机的惯性坐标系,表示为Ogxgygzg。图1为四旋翼无人机的模型结构图。

图1 四旋翼无人机模型结构图Fig.1 Structure of quadrotor UAV model
本文采用单位四元数描述四旋翼无人机的姿态信息。单位四元数定义为Q=[q,η]T=[q1,q2,q3,η]T,可以表示无人机在三维坐标系下的任何旋转。不同于描述姿态的其他方法,单位四元数法只需要在本体坐标系和惯性坐标系下进行四旋翼无人机的旋转估计,而且还避免了“万相锁”现象的产生[13]。由单位四元数表示的从惯性坐标系到本体坐标系的旋转矩阵为:
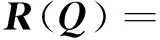
根据欧拉-拉格朗日进行建模,将四旋翼无人机的运动方程简化为:
(1)

2 虚拟控制力设计
将式(1)四旋翼无人机位置子系统模型表达式展开,得到其动力学方程为:
(2)
由式(2)可知,位置子系统有x(t),y(t),z(t)三个状态,控制输入为升力T,可判断出位置子系统为欠驱动系统。由此本文引入了虚拟控制力F=[F1,F2,F3]Τ,使F1,F2,F3分别跟踪x,y,z三个自由度的位置信息。
首先将位置子系统改写为:
(3)
其中:
(4)

式(4)等价为如下方程组:
(5)


3 四旋翼无人机系统控制器设计
四旋翼无人机系统控制器结构如图2所示。首先引入并设计虚拟控制力,使位置子系统控制器跟踪参考位置信息,同时解算出输入升力T和目标姿态Qd。再通过设计控制力矩MΣ,实现对目标姿态Qd的跟踪,从而实现对参考指令信号的跟踪。
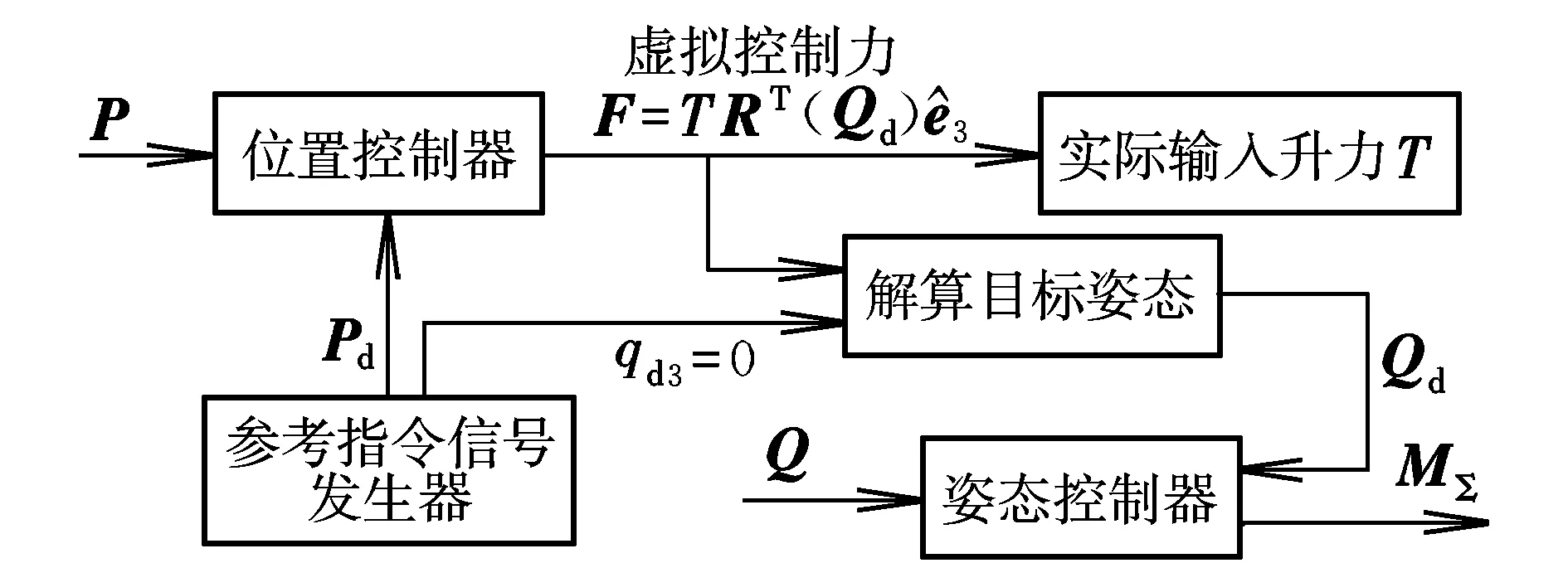
图2 四旋翼无人机系统控制器结构图Fig.2 Structure of quadrotor UAV system controller
3.1 位置子系统控制器设计
假设质量m未知,通过设计自适应滑模控制器得到F的控制律,解算出目标姿态Qd和输入升力T,保证闭环系统的稳定性。
令不确定参数f=m,则式(3)改写为:
其中:

假设不确定参数f是有界的,且f∈R{f:0 (6) 设计虚拟输入力的控制律为: (7) 质量m的自适应律设计为: (8) 3.2 姿态子系统控制器设计 由于m未知造成转动惯量I不确定,因此在姿态子系统控制器设计中,也采用自适应滑模控制方法。姿态子系统模型描述为: 定义误差向量为: (9) 其中: 式中:Ωd为飞行器的目标角速度。 推导出角速度误差模型为: (10) 令不确定参数y=I=diag(y1,y2,y3),则式(10)改写为: (11) 假设不确定参数y是有界的,其范围如下: 输入力矩的控制律设计如下: (12) 令A=[1,1,1]T,惯量矩阵I的自适应律设计为: (13) 其中: 定理:考虑基于欧拉-拉格朗日方法下的系统模型(1),在虚拟控制输入F和控制输入力矩MΣ作用下,整个四旋翼无人机系统稳定。 证明:考虑如下Lyapunov函数: 对其沿系统轨迹求导得: (14) 考虑式(1)给出的四旋翼无人机模型,取质量m=3 kg,重力加速度为9.8 m/s2。其中,系统控制器所需的参数系数和控制增益分别为:c=0.2,γ=2,ks=10,α=4,kβ=10,kq=15,kΩ=15。 假设四旋翼无人机的初始状态为:P(0)=[1,3,2]Τm,v(0)=[0,0,0]Τm/s,I(0)=diag(0.039,0.039,0.039) kg·m2,Q=[0,0,0,1]T,Ω(0)=[0,0,0]T。 目标轨迹为: 图4 质量跟踪仿真结果Fig.4 Simulation results of mass tracking 图5 转动惯量估计值Fig.5 The estimate values of inertia moment 本文在系统参数质量和转动惯量未知的情况下,对四旋翼无人机的轨迹跟踪问题进行了研究。采用单位四元数法对系统姿态进行描述,针对欠驱动特性以及参数的不确定性,采用自适应滑模方法设计虚拟控制律;所提控制方案可以不依赖于模型的精确参数,使四旋翼无人机能够准确跟踪目标。 [1] Islam S,Dias J,Seneviratne L D.Adaptive tracking control for quadrotor unmanned flying vehicle[C]//IEEE/asme International Conference on Advanced Intelligent Mechatronics.Besançon:IEEE,2014:441-445. [2] Xian B,Diao C,Zhao B,et al.Nonlinear robust output feedback tracking control of a quadrotor UAV using quaternion representation[J].Nonlinear Dynamics,2015,79(4):2735-2752. [3] 王璐,李光春,王兆龙,等.欠驱动四旋翼无人飞行器的滑模控制[J].哈尔滨工程大学学报,2012,33(10):1248-1253. [4] Pedro J O,Mathe C.Nonlinear direct adaptive control of quadrotor UAV using fuzzy logic technique[C]//Control Conference (ASCC),2015 10th Asian.Sabah,Malaysia:IEEE,2015. [5] 王焱,宋召青,刘晓,等.一种自适应滑模控制算法在四旋翼无人飞行器中的应用[J].海军航空工程学院学报,2013,28(5):471-474. [6] 甄红涛,齐晓慧,夏明旗,等.四旋翼无人机鲁棒自适应姿态控制[J].控制工程,2013,20(5):915-919. [7] Nicol C,Macnab C J B,Ramirez-Serrano A. Robust adaptive control of a quadrotor helicopter[J].Mechatronics,2011,21(6):927-938. [8] 李瑞琪,王洪福,李瑞雪,等.基于模型参考自适应的四旋翼飞行器控制[J].计算机测量与控制,2013,21(12):3260-3263. [9] Alessandretti A,Aguiar A P,Jones C N.Trajectory-tracking and path-following controllers for constrained underactuated vehicles using model predictive control[C]//2013 European Control Conference (ECC).Linz,Austria:IEEE,2013:1371-1376. [10] 陈向坚,李迪,续志军,等.四旋翼微型飞行器的区间二型模糊神经网络自适应控制[J].光学精密工程,2012,20(6):1334-1341. [11] 杨庆华,宋召青,时磊.四旋翼飞行器建模、控制与仿真[J].海军航空工程学院学报,2009,24(5):499-502. [12] Schreier M.Modeling and adaptive control of a quadrotor[C]//IEEE International Conference on Mechatronics and Automation.Chengdu China:IEEE,2012:383-390. [13] 丁少宾,肖长诗, 刘金根,等.X型四旋翼无人机建模及四元数控制[J].系统仿真学报,2015,27(12):3057-3062. [14] 乔继红,戴亚平,刘金琨.基于非线性干扰观测器的直升机滑模反演控制[J].北京理工大学学报,2009,29(3):224-228. [15] Khalil H K.Nonlinear systems third edition[M].Upper Saddle River,NJ:Prentice-Hall,Inc.,2002. (编辑:李怡) Adaptive tracking control of quadrotor UAV based on sliding-mode control LIU Kai-yue1, LENG Jian-wei2 (1.College of Automation, Tianjin University of Technology, Tianjin 300384, China;2.Key Laboratory of Complex Systems Control Theory and Application, Tianjin 300384, China) An adaptive control method was proposed based on sliding mode control for the trajectory-tracking problem of quadrotor UAV in the presence of model parameter uncertainties. Firstly, the attitude was described using unit quaternion and the system was decomposed into position subsystem and attitude subsystem. Considering the under-actuated characteristics of position subsystem, the virtual control force was introduced to track the position information and calculate the actual thrust and the desired attitude. Secondly, an adaptive sliding-mode controller was designed to compensate the mass uncertainty and moment of inertia uncertainty to guarantee the tracking of trajectory. Finally, the stability of the closed-loop system was proved based on Lyapunov theory. Simulation results show the effectiveness of algorithm. quadrotor UAV; unit quaternion; virtual control force; adaptive sliding-mode control 2016-05-11; 2016-09-06; 时间:2016-11-10 09:10 刘凯悦(1991-),女,山东高唐人,硕士研究生,研究方向为控制科学与工程。 V249.1; V279 A 1002-0853(2017)01-0043-05



4 系统稳定性证明


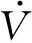
5 仿真验证



6 结束语
