2016年高考浙江理综试卷(物理)第25题评析

徐婷婷

(临海市回浦中学 浙江 台州 317000)

2016年高考浙江理综试卷(物理)第25题评析

徐婷婷

(临海市回浦中学 浙江 台州 317000)

分析了2016年高考浙江理综卷第25题的主要错误之处及失分原因.

错因分析 解题规范 三维目标

2016年高考浙江试卷是浙江现行高考模式的收官之卷.纵观全卷，试题秉承“重视基础、突出思考、联系实际、注重探究”的命题思路，力求稳中求新，同时严格遵照《考试说明》.试题兼顾不同程度考生的具体情况，既完成了知识和能力的考查，又体现出合理的难度和良好的区分度.笔者有幸参加了浙江高考理综试卷第25题的阅卷工作，现将阅卷中发现的考生的主要错误及失分原因作一些分析，并谈一些感想和启发供大家参考.

1 试题及参考答案

1.1 试题呈现

为了进一步提高回旋加速器的能量，科学家建造了“扇形聚焦回旋加速器”.在扇形聚焦过程中，离子能以不变的速率在闭合平衡轨道上周期性旋转.扇形聚焦磁场分布的简化图如图1所示，圆心为O的圆形区域等分成6个扇形区域，其中3个为峰区，3个为谷区，峰区和谷区相间分布.峰区内存在方向垂直纸面向里的匀强磁场，磁感应强度为B，谷区内没有磁场.质量为m，电荷量为q的正离子，以不变的速率v旋转，其闭合平衡轨道如图中虚线所示.

图1 试题题图

(1)求闭合平衡轨道在峰区内圆弧的半径r，并判断离子旋转的方向是顺时针还是逆时针；

(2)求轨道在一个峰区内圆弧的圆心角θ，及离子绕闭合平衡轨道旋转的周期T；

(3)在谷区也施加垂直纸面向里的匀强磁场，磁感应强度为B′，新的闭合平衡轨道在一个峰区内的圆心角θ变为90°，求B′和B的关系.

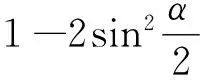
1.2 参考答案

(1)峰区内圆弧半径

旋转方向为逆时针方向.

(2)如图2所示，由对称性，峰区内圆弧的圆心角

每段圆弧的长度

(1)

每段直线长度

(2)

周期

(3)

将式(1)、(2)代入式(3)得

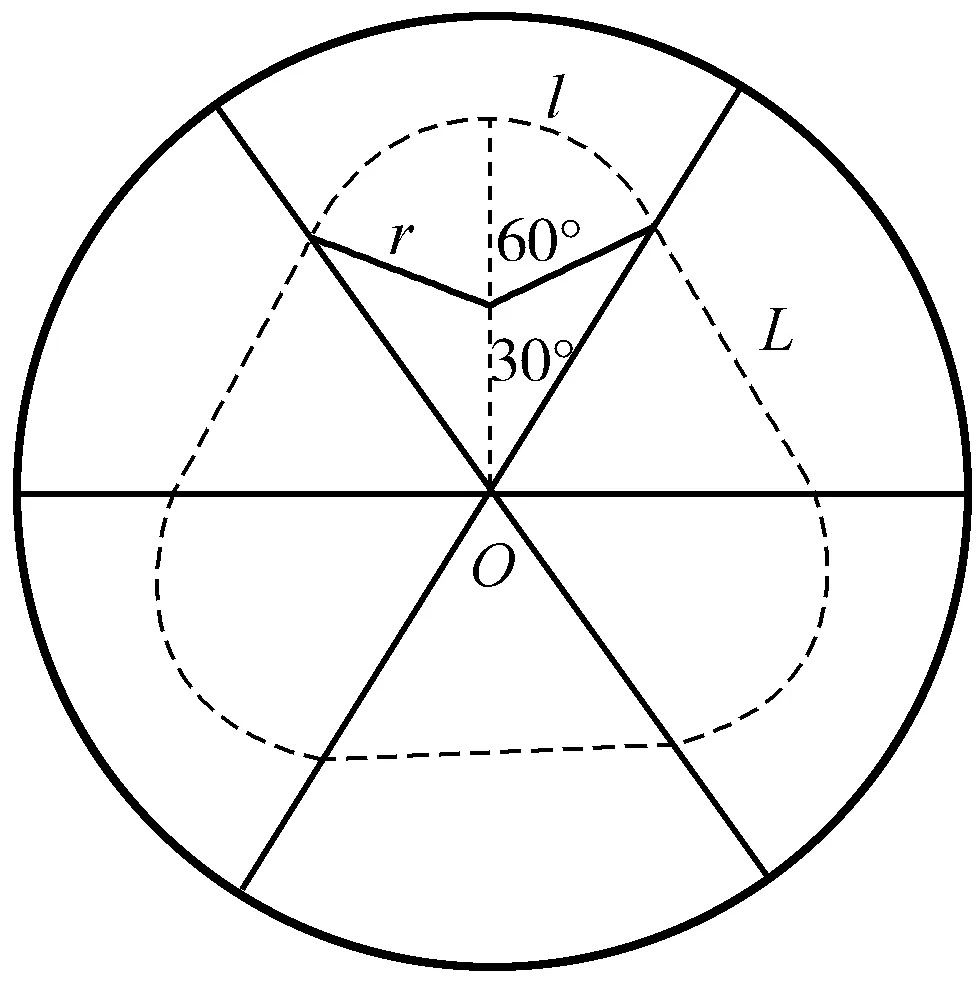
图2 第(2)问分析图

(3)如图3所示,谷区内的圆心角

θ′=120°-90°=30°

(4)

谷区内的轨道圆弧半径

(5)

由几何关系

(6)

由三角关系

(7)

联立式(4)～(7)得

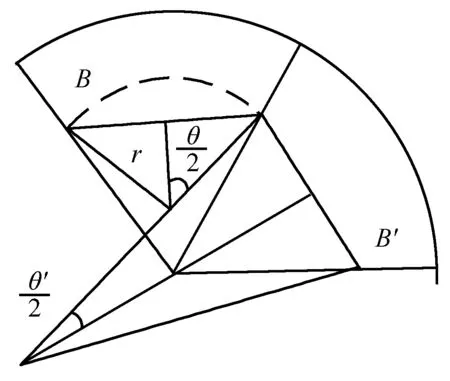
图3 第(3)问分析图

2 试题分析

从知识层面看，本题旨在考查带电粒子在磁场中的运动；从能力层面上看，本题突出考查了考生的推理能力、分析综合能力和应用数学处理物理问题的能力.本题的背景知识体现了试题注重理论联系实际，注重物理学科的自身价值，注重物理知识在生产、生活中广泛应用的特点，有利于激发考生学习科学的兴趣，促进“知识与技能”、“过程与方法”、“情感态度与价值观”三维课程目标的实现.尽管本题在教材基础上引入现代高新科技，但为便于考生建立模型，试题对“扇形聚焦回旋加速器”做了科学的简化，因此对学生建模能力的要求并不高.根据教师和学生的反映情况，2016年这道物理压轴题难度较往年不算太大，涉及的物理模型不多，需要的物理知识涉及面也不大.

3 错因分析

第(1)问在通读题意的基础上，根据磁场方向和正离子所受洛伦兹力的方向，借助左手定则可以判断出正离子的运动方向.再根据题目已知条件“质量为m，电荷量为q的正离子，以不变的速率v旋转”，依据正离子在磁场中做匀速圆周运动，其受到的洛伦兹力提供做圆周运动的向心力， 易得正离子的运动半径.

从高考阅卷的情况看，很多学生从第(2)问开始就出现错误.第(2)问的易错点在于题目所给出的示意图已经画出了正离子的运动轨迹，一些学生想当然地以为正离子运动轨迹的圆心就在圆形区域的圆心O上，因为圆心确定错误，导致圆心角和半径确定错误，进而导致运动周期也错误.然而从图上可知，若轨迹圆心在O点，正离子进入磁场时的速度方向与该点和O点的连线显然不垂直，这是矛盾的.我们可以利用两个速度垂线的交点找圆心，或者利用速度的垂线与弦的中垂线的交点找圆心，这就要求学生熟练掌握“找圆心、求半径”的方法.

第(3)题的难点是两段运动半径不同的匀速圆周运动的衔接.大多数学生都知道在谷区也加上磁场后，离子仍然做匀速圆周运动，但怎样画出运动轨迹，怎样确定圆心位置呢？根据对称性，每个峰区或谷区起到的作用是等效的，整个过程有3对峰区和谷区，正离子运动一周旋转360°，在一对峰区加谷区的区域内旋转120°，已知在一个峰区内旋转90°，那么在一个谷区内就要旋转30°，根据对称性就能将离子在一对峰区加谷区的区域内的运动轨迹补充完整.

第(3)问的另外一个难点就是寻找谷区与峰区内离子运动半径的关系，构建三角形,运用几何关系求解半径关系是本题的关键，这考查了学生应用数学处理物理问题的能力.本题中可以构建的几何关系有多种.现列举如下.

方法1：设在峰区内圆弧轨道的圆心为O1，半径为r，在谷区内圆弧轨道的圆心为O2，半径为r′，如图4所示.

图4 构建的几何关系分析图

由题知∠CO1A=45°，∠AO2D=15°，且CA=AD,所以rsin 45°=r′sin 15°.

方法2：研究对象为△O2AO,由题有

∠O2AO=∠AO2D=15°

所以△O2AO为等腰三角形，过O点作AO2的垂线交于E点,有

故

方法3：研究对象为直角△ADO2,因为

所以在直角△ADO2中

或

方法4：正弦定理

在△O2AO中，∠AOO2=150°，∠AO2O=15°,所以根据正弦定理，有

方法5：余弦定理

在△O2AO中，∠AO2O=15°,所以，根据余弦定理，有

4 教学启发

(1)加强学生的解题规范培养，养成良好的解题习惯

对于试卷中的计算题评分标准也是尽可能地细化至每一步，给出步骤的分值.在阅卷的过程中，发现一些学生对物理情景的理解是正确的，但是没有分步列式而是想一步到位列综合式，结果由于出了一些小错误而导致严重失分.所以，在平常的教学中，一定要认真落实分布解答计算题的解题习惯，在必要时要画出几何关系图并标明字母，让阅卷教师能尽快地理解自己的解题方法.

(2)注重基础知识和基本物理思想方法的教学

笔者认为本题考查的核心就是带电粒子在磁场中运动时“找圆心、求半径、画轨迹”的方法，但这个看似简单的内容却成了学生做题时的拦路虎.通过本题应该看到，日常教学过程中的重点、难点问题同样是考试考查的重点问题，更是具备甄选优秀人才能力的压轴考点.此外，本题很好地展现了物理思想方法中的对称性，教师在平时的教学中应有意识地注重物理思想方法的提炼，训练学生学会从思想方法的高度把握问题.

(3)注重培养学生应用数学处理物理问题的能力

《普通高中物理课程标准》在三维目标的“过程与方法”中，明确提出对应用数学能力的要求，高考物理考纲中也明确提出了要考查学生应用数学工具处理物理问题的能力.物理试题的解答离不开数学知识和数学方法的应用，借助物理知识渗透考查数学能力是浙江省高考命题的一个重要思路.其中解决带电粒子在场中的运动问题，往往需要利用几何图形中的边角关系并结合三角函数来分析.在具体的教学实践中，教师要做好数学思想与方法和物理知识间的相互渗透，长期注重把物理教学与数学教学结合起来，从而达到提高学生应用数学能力的目的.

徐婷婷(1991- )，女，中教二级，主要从事中学物理教学及研究.

2016-08-15)