解析延拓课程教学改革浅探*——兼谈最大熵方法

吕建平

(安徽师范大学物理系 安徽 芜湖 241000)

解析延拓课程教学改革浅探*
——兼谈最大熵方法

吕建平

(安徽师范大学物理系 安徽 芜湖 241000)

针对数学物理方法课程教学中学生普遍反映比较抽象的解析延拓部分，设计以数值模拟方法为技术路线的教学方案.通过物理模型的构建，介绍线性响应理论和最大熵解析延拓方法的基本原理，全面设计课堂教学环节，展示对具体实例的计算结果.最后，对课程实践过程中的有待提高之处进行反思和探讨.

数学物理方法 解析延拓 最大熵方法

数学物理方法课程是高等院校物理类本科专业必修的重要课程之一.然而，对中等程度的学生而言，学好这门课程并不容易.学生在学习过程中既需要高等数学等前期数学课程的良好基础，又需要对一些经典物理模型有清晰的认识[1,2].由于上述客观原因，加之笔者水平所限，在承担安徽师范大学卓越理科实验班数学物理方法课程之初，笔者常在课堂教学设计过程中感到困惑.通过课堂教学的反馈，常获悉学生在学习过程中感到概念过于抽象，无法和具体的物理系统进行有效联系.

和国内多数高校一样，我校数学物理方法课程在低年级开课，此时学生对一些重要物理问题的图像和机理还没有全面的认识.这要求教师在教学过程中，在有限的教学时长内补充介绍相关物理模型.而几乎所有经典教材在讲述偏微分方程部分时都会引入包括电导、热传导在内的输运过程作为主要物理模型.这引发笔者的思考：既然学生在数学物理方法课的学习过程中须对输运过程的物理图像有基本概念，可否将输运过程的相关模型拓展到偏微分方程以外的教学内容？此为笔者探索相关课程设计的背景.

本文讨论解析延拓的教学设计，旨在借助于较为具体的物理图像来避免教学内容过于抽象化，以探索提升教学质量的途径.沿用吴崇试先生《数学物理方法》教材中关于解析延拓的概念[2]: 两个函数f1(z)和f2(z) 分别在定义域g1和g2内解析，且在g1和g2的公共区域等价，则f2(z)可称为f1(z)在g2区域的解析延拓，且f1(z)可称为f2(z)在g1区域的解析延拓.又由同一性原理可知，对定义在同一个区域的两个解析函数，如果它们在该区域内的无穷多个点上相等，且这些点中有聚点存在，这两个函数必然在整个区域上等价.在多体物理系统的研究中常须借助于多种关联函数.在频域复平面上，延迟关联函数和相应的松原关联函数在无穷多个点上相等，且这些点中存在聚点(此处聚点为虚轴上正方向的无穷远点i∞)，因而必然在共同解析区域上等价，且松原关联函数可延拓到延迟关联函数的解析区域.在实际计算中，由于一些数值算法在计算松原关联函数时具有显著的优势.因此，在通常情况下，我们总是先直接计算松原关联函数，再借助于解析延拓手段探索延迟关联函数.

基于上述论证，同时借助于数值模拟方法，笔者将针对输运问题设计解析延拓教学方案，进而在实际教学中进行小范围实践.下文将对教学过程的设计原理和基本环节进行介绍，并对教学实践进行反思和总结.

1 物理问题的提出

输运过程有广泛的范畴，在物理学的教学和研究中具有重要的地位.输运过程研究的常用理论框架之一为线性响应理论.线性响应理论对近平衡态系统的输运行为有良好的描述.根据线性响应理论，我们只需要知道以时间为变量的电流-电流延迟关联函数，就可根据久保公式方便地计算出电导率[3].然而，如何求得电流-电流关联函数？首先，借助于数值模拟可获得电流-电流松原关联函数[4].接下来，可根据解析延拓手段由松原关联函数获得相应区域的延迟关联函数.关于电流-电流松原关联函数的计算，笔者通过前期科研工作已有方法上的积累，既可将程序代码以软件的形式提供给学生使用[5～7]，也可为学生直接提供松原关联函数的数据.无论哪种做法，都不会直接影响学生在解析延拓方面的训练.

在对物理系统平衡态性质的讨论中，基于松原虚时的路径积分蒙特卡洛方法已被广泛采用.然而，本教学过程涉及输运过程的数值实验，对蒙特卡洛方法有更高要求.原因是显然的：此处蒙特卡洛数据只是解析延拓的输入数据，而不再是与实验可比的最终结果.一旦蒙特卡洛数据的精度不高，或抽样数据之间的关联性不能被明确把握，相关的解析延拓过程就难以获得稳定可靠的结果.因此，高效的蒙特卡洛算法是必要的技术手段.在课程教学中，我们将使用高效的蠕虫型连续虚时蒙特卡洛算法，该算法通过新自由度的引入使得位形空间得以扩展，进而以马尔科夫链的形式产生可供抽样统计的位形.这种新位形的产生方式具有克服临界慢化的功能，因而算法效率将获显著提高.在此过程中，学生须知道松原关联函数的形式特点：若考虑频域复平面，在虚轴的松原频率点上松原关联函数可以直接计算，且等同于相应的延迟关联函数.

如前文所述，在物理上更重要的是实时延迟电流-电流关联函数.若已知松原关联函数在上半平面内一些点上的数值结果，如何通过解析延拓，获得无限靠近实轴时的关联函数数据？不失一般性，在已获得松原关联函数数据的情况下，可通过最大熵解析延拓办法获得以实频为变量的延迟关联函数，进而求得电导率.

2 最大熵解析延拓方法

通过多体物理理论中常用的莱曼(Lehmann)谱分解可知，在远离实轴的上半频域复平面内，延迟关联函数在形式上等价于相应的松原关联函数.在松原频率上，后者可由量子蒙特卡洛模拟直接测量.为探索实轴上的信息，可作解析延拓iωn→ω+i0+，其中ωn为松原频率.我们拟采用的最大熵方法是最具代表性的解析延拓方法之一[8,9].最大熵方法的主要思路是运用贝叶斯推理，把寻找最可能解析延拓结果的问题，转化为求解“自由能”最小值的问题，它的稳定性已被大量文献结果所证实.值得一提的是，最大熵方法对具有数值不确定性的数据具有强大的处理能力.在实际应用中，我们借助于高效量子蒙特卡洛方法产生的松原关联函数具有高度的精确性，完全可以通过最大熵方法获得稳定可靠的实频输出数据.另外，我们拟定的课堂教学方案中也包含了可靠的误差估计方法.他山之石，可以攻玉.在未来的教学过程中，我们也有可能借鉴其他的解析延拓方法，如随机优化方法[10]和随机抽样方法[11]，将它们作为传统最大熵方法的重要补充.

最大熵方法最早发展于工程科学领域，后被物理学家借鉴，用来解决具有数值不确定性数据的解析延拓问题[8].首先，根据相关问题情境，引入“自由能”的概念.“自由能”的定义为F=χ2-AS，在形式上与热力学中的自由能类似，其中χ2是描述拟合过程的协方差，S是相对于预设默认模型的熵密度，A是常系数，它的选取有不同的判定方法.而S类似于热力学中的熵，此即为最大熵方法名称的由来.我们不难想象，当A=0时，F中协方差χ2占主导地位，解析延拓过程就完全退化为数据拟合过程，拟合结果通常为噪声结果，不具有预测能力；当A很大时，S占主导作用，拟合结果对应于平庸的默认模式.这两种极限下，解析延拓结果都没有意义.实际上，根据χ2随熵权重变化的依赖关系可区分3个截然不同的区域：噪声拟合区域、信息拟合区域和默认模型区域.对这3个区域的探讨和分析，将有助于我们正确使用并最终发展最大熵方法[9].

在通过编程实现解析延拓的过程中，我们会尽可能地纳入有效信息而完全避免噪声信息.为此，我们把噪声拟合区域和信息拟合区域的分界点作为熵权重的最佳选择，并通过分析不同类型的熵权重选择方法，探索最佳的解析延拓方案.从理论上讲，无论输入数据是否有数值上的不确定性，最大熵方法都应该给出唯一稳定的解析延拓结果.但值得注意的是，熵权重的选取会影响误差估计的可靠性.而目前较为流行的熵权重选取方法是基于经验判据，即令协方差χ2等于样本数.该判据仅在样本数很大且χ2精确可知的情况下较好地工作，因而不是我们的选择.

3 课堂教学的实例

根据输运过程的基本特征，借助于相关的理论和方法，并考虑课堂教学的实际情况，我们拟定了如图1所示的课堂教学基本流程.

其中T为温度，kB为玻尔兹曼常数.若仅关注平衡态行为，通过附加的模拟可确定此时系统处于正常流体态，其低温下的超流特性被热涨落破坏，但仍然保留普通流体的一些特征，包括扩散性和可压缩性.我们在前文中提到的蒙特卡洛方法对该系统具有较为强大的刻画能力.

图1 课程教学的基本流程

通过数值模拟，我们获得了系统在平衡态的一系列数据.在图2中，我们展示了以虚频为自变量的电流-电流松原关联函数.不难发现，该函数以较快的速度衰减.又由线性响应理论可知，以实频为变量的电流-电流延迟关联函数的虚部与电导率的规则项对应.为获得该延迟关联函数的虚部，我们采用上文中提到的、经过优化的最大熵方法进行解析延拓.如图3所示，我们获得了电导率随实频率变化的关系.和我们的预期一致，相关的解析延拓手段展现出高度的精确性和稳定性，这一点体现为解析延拓结果极窄的上下界范围.最后，我们将直流(ω=0)电导率的规则项确定为0.085(2).

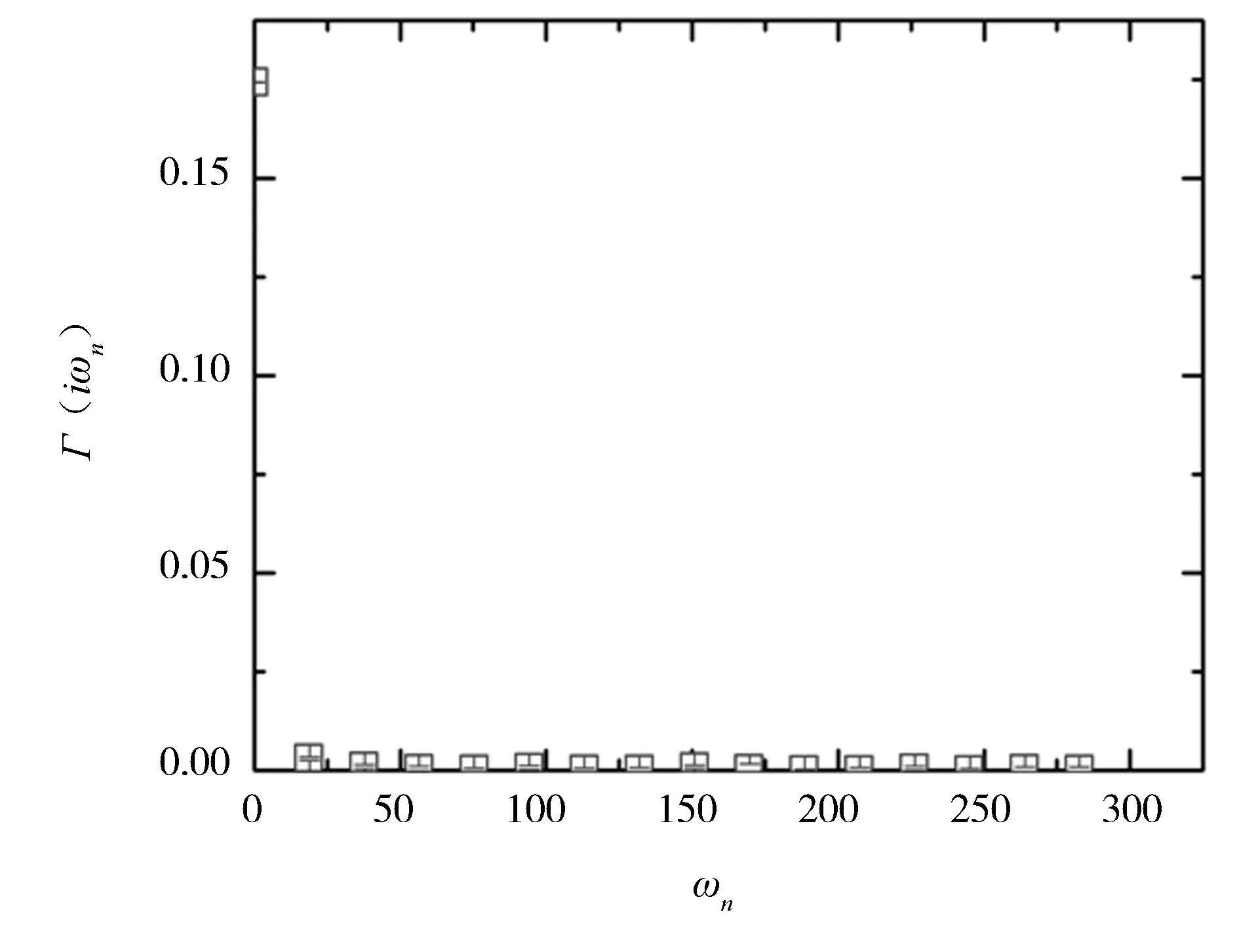
图2 高温下正常流体态的松原流-流关联强度(已设=1，

图3 高温下正常流体态的电导率，所取参数与图2相同

4 总结和反思

通过将数值模拟方法引入到解析延拓课程相关章节的教学过程中，学生可获得对解析延拓理论及其实践方法的直观印象.通过与实际物理问题的结合，学生意识到相关教学内容在现代物理研究中的重要性，因而在一定程度上增强了学习的积极性.然而，笔者也清楚地认识到教学过程中的若干不足之处.例如，产生松原关联函数的过程对学生而言类似于一个“黑匣子”，学生很难全面地理解数值模拟的细节，这可能会在一定程度上削减学生参与相关数值实验的热情.在数学物理方法课程的教学中，如何在有限的教学时长内，让学生通过课本知识获得完整解决一个实际物理问题的体验？以本文为起点，在后续的教学实践过程中，笔者将继续修正相关的课程教学环节，以期获得教学效率的持续提高.

1 四川大学数学学院高等数学、微分方程教研室．高等数学(第4册)(第3版).北京: 高等教育出版社, 2010.76～98

2 吴崇试.数学物理方法.北京：北京大学出版社, 1999.137～144

3 列夫·达维多维奇·朗道,E·M·栗弗席兹.理论物理学教程:统计物理学(第5版)．束仁贵,束莼，译.北京:高等教育出版社,2011.337～347

4K.Binder(edit.).TheMonteCarloMethodinConden-sedMatterPhysics.Germany:Springer, 2012

5J.P.Lv,Q.H.Chen,Y.Deng.Two-specieshardc-orebosonsonthetriangularlattice:AquantumMonteCarlostudy.Phys.Rev.A, 2014,89:013628

6J.P.Lv,G.Chen,Y.Deng.Z.Y.Meng,CoulombliquidphasesofbosonicclusterMottinsulatorsonapyrochlorelattice.Phys.Rev.Lett.115,2015:037202.

7J.P.Lv.Kaleidoscopeofsupersolidphasesofinterac-tinghard-corebosonsonthedicelattice.TheEuropeanPhysicalJournalB,2015,88:13

8M.Jarrell,J.E.Gubernatis.Bayesianinferenceandtheanalyticcontinuationofimaginary-timequantumMonteCarlodata.PhysicsReports1996, 269:133

9D.Bergeron,A.M.S.Tremblay.Algorithmsforopti-mizedmaximumentropyanddiagnostictoolsforanalyticcontinuation.arXiv, 2015, 1507.01012

10A.S.Mishchenko.StochasticOptimizationforAnalyt-icalContinuation:WhenaprioriKnowledgeisMissing, 14thchapterinCorrelatedElectrons:FromModelstoMaterials.ed.byE.Pavarini,W.Koch,F.AndersandM.Jarrell,VerlagdesForschungszentrumJülich, 2012: 1～24

11A.W.Sandvik.Stochasticmethodforanalyticcontinu-ationofquantumMonteCarlodata.Phys.Rev.B,1998, 57:10287

ExplorationontheTeachingReformofAnalyticContinuationCourse——AndTalkingabouttheMaximumEntropyMethod

LvJianping

(DepartmentofPhysics,AnhuiNormalUniversity,Wuhu,Anhui241000)

For the analytic continuation part in Mathematical Physics course which is more or less abstract to students, we design the course teaching based on numerical simulation methods. In this paper, via the construction of physical model, we introduce the basic aspects for linear response theory and maximum entropy analytic continuation method. We design the specific procedure in course teaching process, and demonstrate the numerical results for a specific example. Finally, we discuss the possible directions to improve present course teaching process.

Mathematical Physics; analytic continuation; maximum entropy method

*国家自然科学基金，项目编号：11405003,11147013

吕建平(1983- )，男，博士，主要从事数学物理方法、群论和大学物理等课程的教学，以及凝聚态物理理论研究.

2016-06-19)