高中物理教学中两种力的平均值的比较
2017-02-15殷勇
殷 勇
(武汉市黄陂区第一中学 湖北 武汉 430300)

高中物理教学中两种力的平均值的比较
殷 勇
(武汉市黄陂区第一中学 湖北 武汉 430300)
在高中物理教学中,会遇到变力在两种不同情况下求平均值问题,笔者通过两例对这两种情况做了分析.
力的平均值 时间 位移
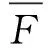
【例1】在水平光滑的地面上有一质量为m的木块,从某时刻计时t=0,对物体施加一水平外力,方向不变,大小与时间成正比,即F=kt,图像如图1所示.物体在外力作用下沿力方向做加速运动.在t=t0时刻,物体的位移s=s0,则在此过程中,力随位移的变化关系图像大致是( )
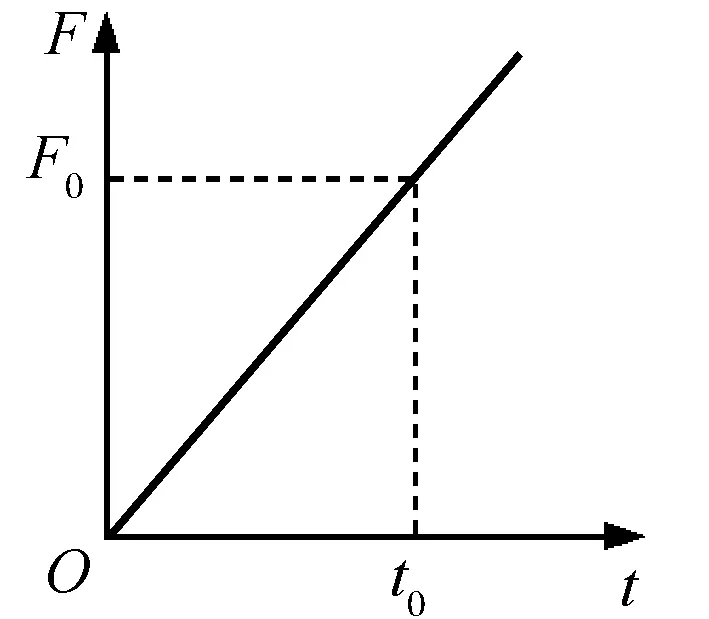
图1 例1题图
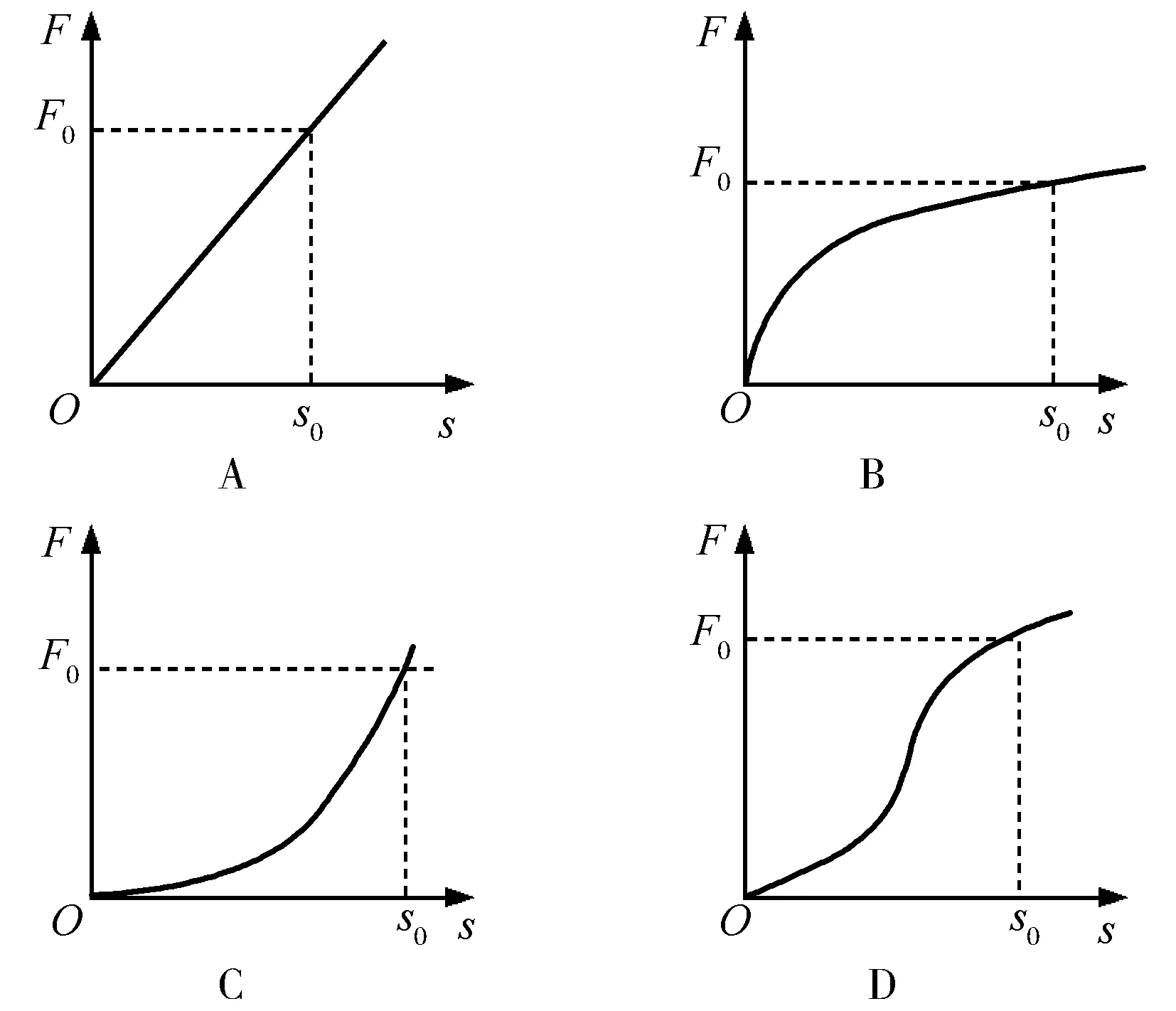
部分学生认为力对时间是线性的则力对位移也是线性的,会错误地选A.而绝大部分学生不知道力对时间的函数与力对空间的函数的变换,即使选对也是蒙的.
物理学研究对象是物质世界的时空规律(运动性),因此要理解力对时间的函数和力对空间的函数,必须从物体运动特征出发.
设某时刻的速度为v(t),则
F=kt
t时刻对应的位移为s(t),则
所以F-s的关系为
由函数关系得答案为B.
由于数学能力限制学生不能求出力对位移的函数关系,但在高中阶段可以利用图像斜率的变化来分析.
木块在外力F作用下做的是加速度变大的加速运动.在运动过程中任意取两个时间间隔相同的时段,设时间间隔为Δt,由F-t图像可知这两个时间间隔内力的改变量ΔF相同.由于物体做的是加速度变大的加速运动,则后一个时间间隔的位移Δs后大于前一个时间间隔的位移Δs前,所以
F-s图像中斜率越来越小,答案选B.
从上面分析可知,变力过程的两种平均值并不是相同的.力对时间是线性关系,则力对位移就不一定是线性关系.下面再探讨一下,力对位移是线性关系,那么力对时间会是怎样的变化?
【例2】如图2所示,水平弹簧振子的质量为m,弹簧的劲度系数为κ,振幅为A.求弹簧振子从最大位移B处到平衡位置C处的过程中,弹力的冲量和功是多大.
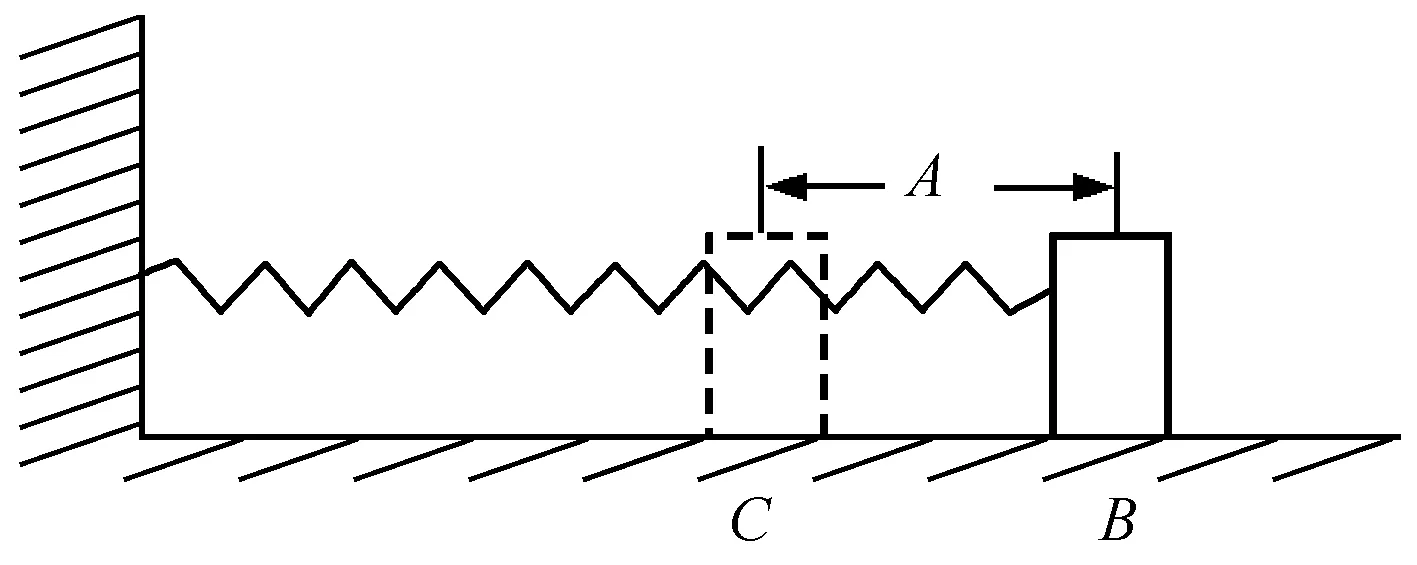
图2 例2题图
分析:振子从B到C运动的过程中,弹簧的弹力是一个变力,设法求出过程中的平均力,就可以求出弹力的冲量和功.
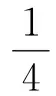
又因弹簧弹力的大小为F=κx,而
所以
即F是时间t的余弦函数.
当t=0时,F有极大值,Fmax=κA,这是振子在B处时的情形.
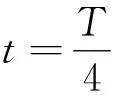
振子的F-t图像如图3所示.
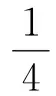
所以弹力的冲量为
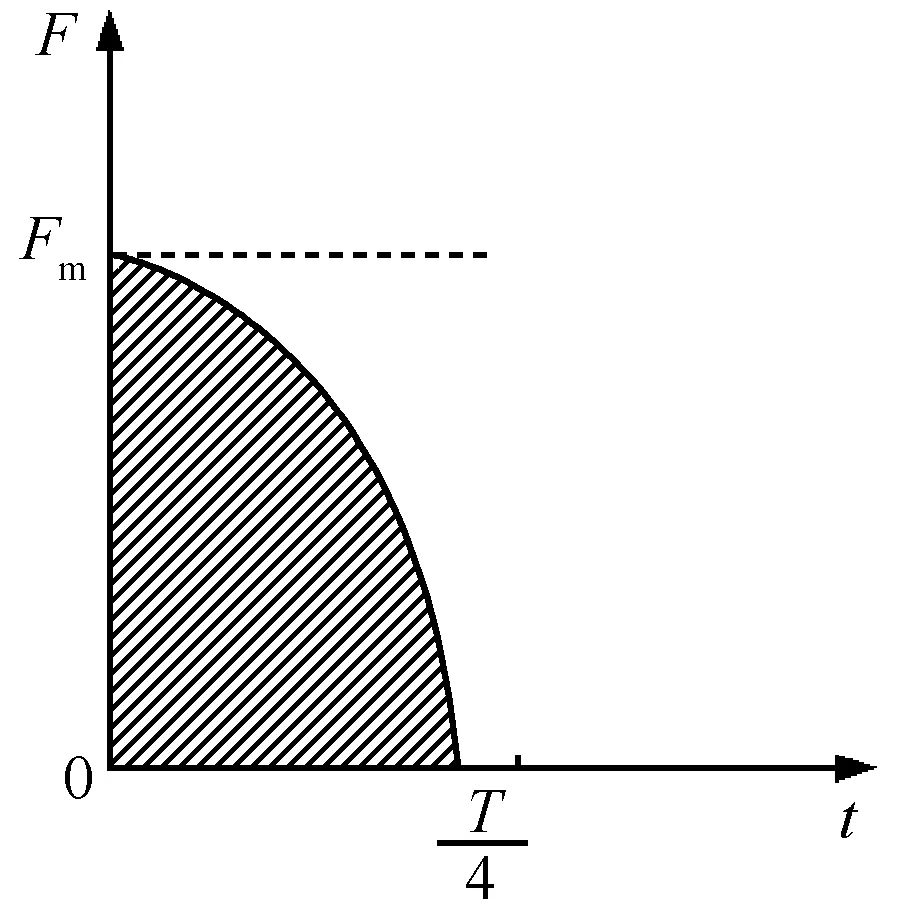
图3 F-t图像
以平衡位置C为参照点,由胡克定律得F=κx,所以力对位移的图像如图4所示.
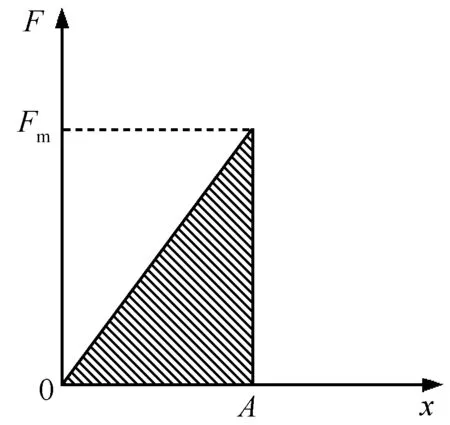
图4 F-x图像
而在B到C过程中F对空间的平均值为
所以弹力的功为
从上面分析可知力对位移是线性关系,但力对时间就不一定是线性关系.
一般只有在一维空间的情况下,动能定理求出的平均力是对位移的平均值,反映的是变力在空间上的累积效果,对应的是变力做功的过程.利用动量定理求出的平均力是对时间的平均值,反映的是变力在时间上的累积效果,对应的是变力的冲量过程.
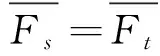
由动量定理
两式相除得
这个结果说明研究对象一定做匀变速运动.显然这与变力作用下物体的运动状态不符合.对位移的平均值和对时间的平均值是两种不同的平均方式,这两种不同的平均方式体现了不同的物理思想,在运用中不能混淆.由于动量是矢量,动能是标量,动量更能明确描述物体运动状态的改变.有些问题中,可以用动量定理求变力的平均值,而不能用动能定理求变力的平均值.例如完全弹性碰撞中,产生的弹力是一个变力,作用过程中,作用时间不为零,作用过程的位移可能为零,则此时用动能定理是无法求解的.
ComparisononMeanValuesofTwoKindsofForcesinSeniorHighSchoolPhysicsTeaching
YinYong
(HuangpiNo.1HighSchool,Hubei,Wuhan430300)
In high school physics teaching, the questions about solving the mean values of variable forces are often encountered, the author analyses the two situations through two cases.
mean values of force; time; displacement
2016-07-14)
