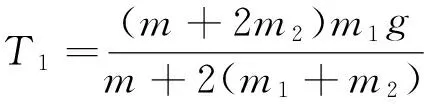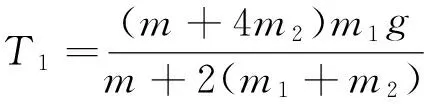高中物理中的“轻模型”
2017-02-15张郑兵
张郑兵
(安徽省庐江中学 安徽 合肥 231500)
房 英
(庐江第二中学 安徽 合肥 231500)
高中物理中的“轻模型”
张郑兵
(安徽省庐江中学 安徽 合肥 231500)
房 英
(庐江第二中学 安徽 合肥 231500)
通过例题研究了不同类型 “轻物体” 的动力学问题,探讨了不同类型“轻物体”的动力学特点,希望对广大学生和教学同仁有一定借鉴意义.
轻物体 轻模型 牛顿第二定律 合力为零
高中物理中描述一类物体时常在其前面加上限定词“轻”,如“轻结点”、“轻绳”、 “轻弹簧” 、“轻杆”、“轻滑轮”等.“轻”主要可以理解为物体质量对所研究的物理问题影响很小,可以忽略不计.这类物体我们可以把它叫做“轻物体”,利用牛顿运动定律我们可以建立“轻模型”来加以研究.由牛顿第二定律可以得出轻物体所受合力必然为零的特点,与其运动状态无关.这一特点通常是理解相关试题的切入点和突破口,然而学生对这一特点往往感到困惑.
所谓 “轻物体”,指的是质量可以忽略不计的物体,是一种理想化的物理模型.然而学生对这类物体缺乏感性认识,研究这类物体时的思维方式又与常规物体有很大差异,导致学生通常感觉这类问题难度甚大,无从下手.
要认清“轻物体”这一模型,首先要分清“轻物体”和 “重力不计的物体”的区别.“轻物体”质量可忽略,从而亦可以忽略其重力.“重力不计的物体”在电磁学中常有涉及,通常说明带电粒子 “重力不计”,即受力分析时不考虑其重力,但质量不能忽略,可由牛顿第二定律求出合力,再计算加速度.
其次,要清楚“轻物体”的受力特点.根据牛顿第二定律,物体加速度与其合外力、质量的关系F=ma,由于“轻物体”质量为零,无论其加速度多大,所受合外力必然为零,与物体的运动状态无关.这也是它与常规物体的最大区别,也是学生感到最为困惑的地方.
近几年高考对“轻物体”问题常有考查且学生失分较多.高中学习中常涉及到的“轻结点”、“轻绳”、“轻杆”、“轻弹簧”、“轻滑轮”都属于这类问题.下面我们就通过例题探讨不同类型“轻物体”的动力学特点.
1 轻结点(环)
【例1】(2016年高考课标全国Ⅲ卷)如图1所示,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a,b间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )

图1 例1题图
解答:受力分析如图2所示,设圆弧的圆心为O,悬挂小物块的点为c,左右两个小球的悬点分别为d,e.题中绳子结点均光滑,实际上是一根绳,各段绳子上弹力大小一定相等,且T=mg.对左侧轻环研究,由于其质量极小,重力可忽略不计,所受合力为零.左环受到的3个力分别为ad绳拉力,ac绳拉力,以及圆弧的弹力.圆弧弹力背离圆心,所以ad和ac绳拉力的合力一定指向圆心且在这两绳夹角的平分线上.令
∠Oac=∠Oad=θ
由于ab=R,所以三角形Oab为等边三角形,根据几何知识可得
∠Oab=60°θ=30° ∠acb=120°
而在一条绳子上的张力大小相等,故有
T=mg
小物块受到两条绳子的拉力作用大小相等,夹角为120°,故受到的两绳拉力的合力等于mg,因为小物块受到绳子的拉力和重力作用,且处于平衡状态,故拉力的合力mg等于小物块的重力,所以小物块的质量为m,故A,B,D错误,C正确.
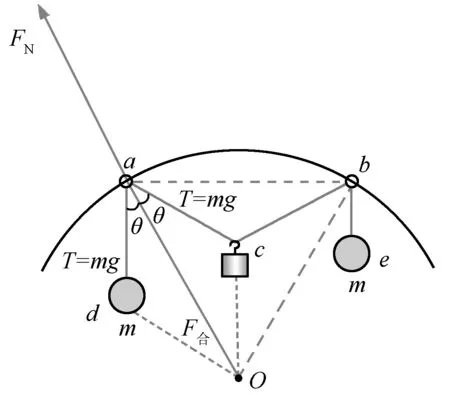
图2 例1分析图
2 轻绳
【例2】(2011年高考江苏卷)如图3所示,倾角为α的等腰三角形斜面固定在水平面上,一足够长的轻质绸带跨过斜面的顶端铺放在斜面的两侧,绸带与斜面间无摩擦.现将质量分别为M和m(M>m)的小物块同时轻放在斜面两侧的绸带上.两物块与绸带间的动摩擦因数相等,且最大静摩擦力与滑动摩擦力大小相等.在α角取不同值的情况下,下列说法正确的有( )

图3 例2题图
A.两物块所受摩擦力的大小总是相等
B.两物块不可能同时相对绸带静止
C.M不可能相对绸带发生滑动
D.m不可能相对斜面向上滑动
解析:本题中绸带质量不计且斜面光滑,可将绸带等效为一根轻绳,其所受合力必然为零,故无论任何情况下绸带对两物块的摩擦力大小均相等,A选项正确.接着可以仔细分析本题中两物块所有可能的运动状态.
假设M相对绸带发生滑动,其对绸带的滑动摩擦力为μMgcosα,而m对绸带的摩擦力最多为μmgcosα,由于μMgcosα>μmgcosα,绸带所受合力不为零,假设不成立.故M不可能相对绸带滑动,它受到绸带的静摩擦力作用.若M相对斜面静止,其所受摩擦力等于Mgsinα,此时m亦受到Mgsinα的摩擦力从而会加速上滑,绸带发生松弛,不符实际.若M相对斜面向上运动,同样可分析得出m会向上加速运动,假设同样不成立,故M必定向下加速.对二者的状态分析如表1所示.
表1M和m状态分析
若m也受到绸带静摩擦力作用,有一种可能的情况:M向下加速,m向上加速,且二者加速度相等.
若m受到滑动摩擦力作用,需讨论m受到的滑动摩擦力和重力沿斜面向下分力的关系,此情境有3种可能情况:若μmgcosα>mgsinα,m会向上加速;若μmgcosα=mgsinα,m相对斜面静止;若μmgcosα>mgsinα,m向下加速.
由此分析可知C正确,B,D错误.本题答案:A,C.
对M,m所有可能的运动情境,可结合上面系统表直观看出.
3 轻弹簧
【例3】如图4所示,4个完全相同的轻质弹簧都处于水平位置,他们的右端受到大小皆为F的拉力作用,而左端的情况各不相同:①中弹簧的左端固定在墙上,②中弹簧的左端受大小也为F的拉力作用,③中弹簧的左端拴一小物块,物块在光滑的桌面上滑动,④中弹簧的左端拴一小物块,物块在有摩擦的桌面上滑动.若认为弹簧的质量都为零,以l1,l2,l3,l4依次表示4个弹簧的伸长量.则有( )

图4 例3题图
A.l2>l1B.l4>l1
C.l1>l3D.l2=l4
解析:多数学生能分析出①、②两种情况实际是一种情况,得出l1=l2的结论.但是要比较③、④以及它们与①、②的区别往往就无法下手了.对于③、④两种情况,很多学生主观上认为④中桌面粗糙,对弹簧的拉力更大,从而得出l4 (1)若弹簧的劲度系数为κ,求轻杆开始移动时,弹簧的压缩量x; (2)求为使装置安全工作,允许该小车撞击的最大速度vm; (3)讨论在装置安全工作时,该小车弹回速度v′和撞击速度v的关系. 图5 例4题图 解析:本题的第一个问题较为简单,弹簧弹力等于杆受到的最大静摩擦力时轻杆就开始移动,由胡克定律可求出弹簧的压缩量.对后面两个问题解题的突破口是理解轻杆运动后弹簧的形变情况.对于轻杆而言,其质量为零合力必然为零,轻杆向右运动过程中所受滑动摩擦力不变,故而轻弹簧弹力不变,弹簧压缩量不变,小车与轻杆保持相对静止一起匀减速到零.然后杆保持静止状态,小车在弹簧弹力作用下向左加速直至弹簧恢复原长后,小车与弹簧分离. (1)轻杆开始移动时,弹簧的压缩量为x,由胡克定律得弹簧的弹力F=κx,轻杆所受合力为零,即F=f,联立解得 (2)设轻杆移动前小车对弹簧做功为W,对小车从撞击到速度减为零的过程中,由动能定理得 同样,以最大速度vm撞击时,有 联立解得 (3)设小车以速度v1撞击弹簧恰使轻杆移动,有 结合(2)可解得 讨论: 1)当 时,杆未动,小车的动能先转化为弹簧的弹性势能,弹性势能最终又转化为小车的动能,小车仍以原速弹回,即弹回速度 v′=-v 2)当 时,可使轻杆移动,且保证装置安全工作.系统速度减到零后,小车反弹,弹簧的弹性势能转变为小车的动能.可得出弹回速度 拓展思考:假设小车撞击为安全速度,且撞后立即与弹簧栓连,问最终杆和小车所处的状态? 栓连后小车压缩弹簧的过程和题中问题没有区别,小车被弹开过程在水平方向做简谐振动,根据简谐运动的对称性,弹簧的最大伸长量与最大压缩量相等,无法使杆运动,故最终杆静止,小车做简谐振动. 【例5】(2011年高考福建卷)如图6所示,一不可伸长的轻质细绳跨过滑轮后,两端分别悬挂质量为m1和m2的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的摩擦.设细绳对A和B的拉力大小分别为T1和T2,已知下列4个关于T1的表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析判断正确的表达式是( ) 图6 例5题图 解析:本题中出现的滑轮是有质量的,学生在高考环境中遇到此题的时候可能会觉得无从下手,甚至会怀疑高考复习中可能有遗漏的知识盲点.实际上利用高中知识是无法解决有质量滑轮转动问题的.那么是不是意味着本题我们就无计可施了呢? 做选择题无从下手的时候,特殊值法往往能起到出其不意的效果.本题最大的难点就是不会处理有质量的滑轮,那么如果把滑轮质量假设为零呢? 设m=0,滑轮即为轻滑轮,它受到两端绳拉力大小必然相等.可令T1=T2=T. 若m1 T-m1g=m1a 对B,有 m2g-T=m2a 可得到 把m=0代入A,B,C,D 4个选项,得C选项符合. 理论拓展:不少学生有疑问,对于质量m不可忽略的滑轮,难道细绳对A和B的拉力大小分别为T1和T2,二者不相等了吗?确实不等! 物体加速运动过程中,滑轮也在加速转动,题中说明“不计滑轮与轴之间的摩擦”,因而滑轮与轴间的摩擦力矩为零,轴对滑轮的支承力不产生力矩,可知两侧绳拉力对滑轮的合力矩不为零,因而拉力不等.结合大学物理中“刚体转动”方面的知识,可有如下解答过程. 假设m1 (T2-T1)r=Jβ (1) 其中转动惯量 角加速度 式中a为物体加速度. 将以上物理量代入式(1)有 (2) 根据牛顿第二定律,对A,有 T1-m1g=m1a (3) 对B,有 m2g-T2=m2a (4) 由式(2)、(3)、(4)可求出 值得注意的是,滑轮质量不可忽略的问题在高中物理实验中也有所体现,如在“验证机械能守恒”实验中,滑轮转动动能的增加是比较重要的实验系统误差,因此实验中应尽量选取质量小的滑轮. 综上所述,解决“轻物体”模型的关键在于理解其质量为零的特点,由牛顿第二定律分析得出“轻物体”所受合外力为零的规律,而与物体的运动状态无关.要区分“轻物体”与一般物体的不同,避免形成思维定势,注意具体问题具体分析,并在解题中磨练,做到熟能生巧. 1 姜胜,任才生,潘华君.“轻质问题”初探. 中学物理,2013,31(11):94~95 2 王玉霞.轻质物体——一个永远“平衡”的物体.物理教学探讨,2014,32(12):43~44 3 李建斌.高考中的轻质物体.中学物理教学参考,2014(20):60~61 TheLight ModelinHighSchoolPhysics ZhangZhengbing (LujiangMiddleSchoolAnhuiProvince,Hefei,Anhui231500) FangYing (LujiangNo.2MiddleSchoolAnhui,Hefei,Anhui231500) In this paper, we study the dynamics of different types of "light objects",discuss the dynamic characteristics of different types of "light objects", and hope to have a certain reference to the majority of students and teaching colleagues. light objects; light model; Newton′s second law; zero external force 2016-08-02)4 轻杆
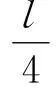

5 轻滑轮