含剪力销(锥)螺栓法兰连接结构弯剪扭耦合振动研究

芦 旭, 张宇航, 陈 岩, 毛鹏程, 余 飞, 关振群

(大连理工大学 工程力学系/工业装备结构分析国家重点实验室，辽宁 大连 116024)

含剪力销(锥)螺栓法兰连接结构弯剪扭耦合振动研究

芦 旭, 张宇航, 陈 岩, 毛鹏程, 余 飞, 关振群

(大连理工大学 工程力学系/工业装备结构分析国家重点实验室，辽宁 大连 116024)

大型工业装备中的连接结构，往往处于复杂多样的外载荷环境中，其振动特性分析尤为重要。针对含剪力销(锥)的螺栓法兰连接结构的振动特性开展研究，根据该类结构在实际工况中受弯、剪、扭组合作用的特点，建立了两种多自由度的质量-非线性弹簧系统，分别讨论了系统在弯剪组合作用以及扭转作用下的振动特性、耦合关系。在此基础上，研究锥角不同、装配间隙不同对螺栓最大拉力的影响，并给出相应关系图；指出在两种工况下剪力销最佳设计角度区间及相应的装配间隙。

连接结构；剪力销(锥)；非线性；耦合振动；装配间隙

螺栓法兰连接以及销式连接在许多大型机械、航空航天器中作为主要的连接支撑结构，箭体级间段的对接，核电站转动轴的装配都是极其典型的例子。这两种连接系统的动力学行为在不同条件下极为复杂[1-2]。因此，研究其在各种工况下的振动特点，分析装配间隙对该类结构动力学响应的影响就变得十分必要。

目前，连接结构形式多种多样，粘结工艺及其修复技术发展迅速[3]，螺栓法兰连接仍是作为主要连接手段广泛应用于航空航天、机械能源等领域。许多研究都是针对螺栓连接区域建立简化二维轴对称模型进行数值分析，用有限元计算及实验测试来探究滑移摩擦、屈服效应、动态响应传递关系等力学行为[4-7]。此类研究重心为连接局部分析，而LUAN等[8]把轴向拉压不同的刚度模型引入螺栓法兰连接结构中，将整体结构通过对称关系简化为两自由度的弹簧-质量系统，并给出了系统纵向与弯曲方向的耦合关系。

诸如外载荷工况、结构局部设计以及装配间隙都是影响连接结构振动特性的主要因素[9-11]。CHEN等[12]通过改变间隙设计参数，提出一种可以使临界区域最大第一主应力缩减30.39%，最大冯·米塞斯应力缩减25.34%的方法。KIRAL[13]对板的几何尺寸、销的直径对销式连接失效影响作出评价，发现装配间隙与过盈配合是机械连接部件失效的重要影响参数。王花娟等[14]分析表明装配间隙是影响连接强度的重要因素, 螺栓连接复合材料的挤压强度和最大破坏强度均随着间隙的增加而下降, 且下降程度很相似。在连接结构研究中，诸多相关因素对连接结构动力学影响及振动特性的研究还有待拓展。

本文分别建立了弯剪作用下的三自由度质量-双线性弹簧系统，以及扭转作用下的二自由度质量-双线性弹簧系统，两系统在工程结构上是相互对应的。在忽略摩擦、刚性接触等假设下分析两个系统的动力学特征。研究发现，两种工况下系统横向、扭转与纵向都存在振动耦合关系，给出不同倾角下剪力销对系统螺栓最大拉力的影响包络，并讨论了两种工况、不同剪力销倾角、不同装配间隙下螺栓最大拉力的变化趋势。这些结果对含剪力销(锥)的螺栓-法兰连接结构的优化设计具有重要的现实意义。

1 理论模型-含剪力销(锥)螺栓法兰连接结构

1.1 螺栓-剪力销受力机理分析

含剪力销(锥)的螺栓-法兰连接(图1)通过法兰盘、螺栓、剪力销之间的相互接触对力进行传递。根据其连接特点，接触面在动力学振动环境下，接触区较小，对接面存在间隙；并且，我们所研究的特定目标处于强振动和一定湿度的环境中，摩擦系数比一般条件下大大降低，因而本文假定忽略摩擦力[15-16]；同时，讨论中去除摩擦引起的能量耗散会使整个系统分析偏于更加安全的考虑。在弹性变形阶段，螺栓可简化为轴向拉压刚度不同的双线性弹簧，剪力销采取同样简化方法。值得注意的是，若剪力销处存在装配间隙，系统受横向冲击或扭转作用时，一端法兰通过滑移接触剪力销后，剪力销开始对系统产生作用。此时，将系统接触问题及结构非线性问题转化为材料非线性问题进行处理。如(图2和图3)。

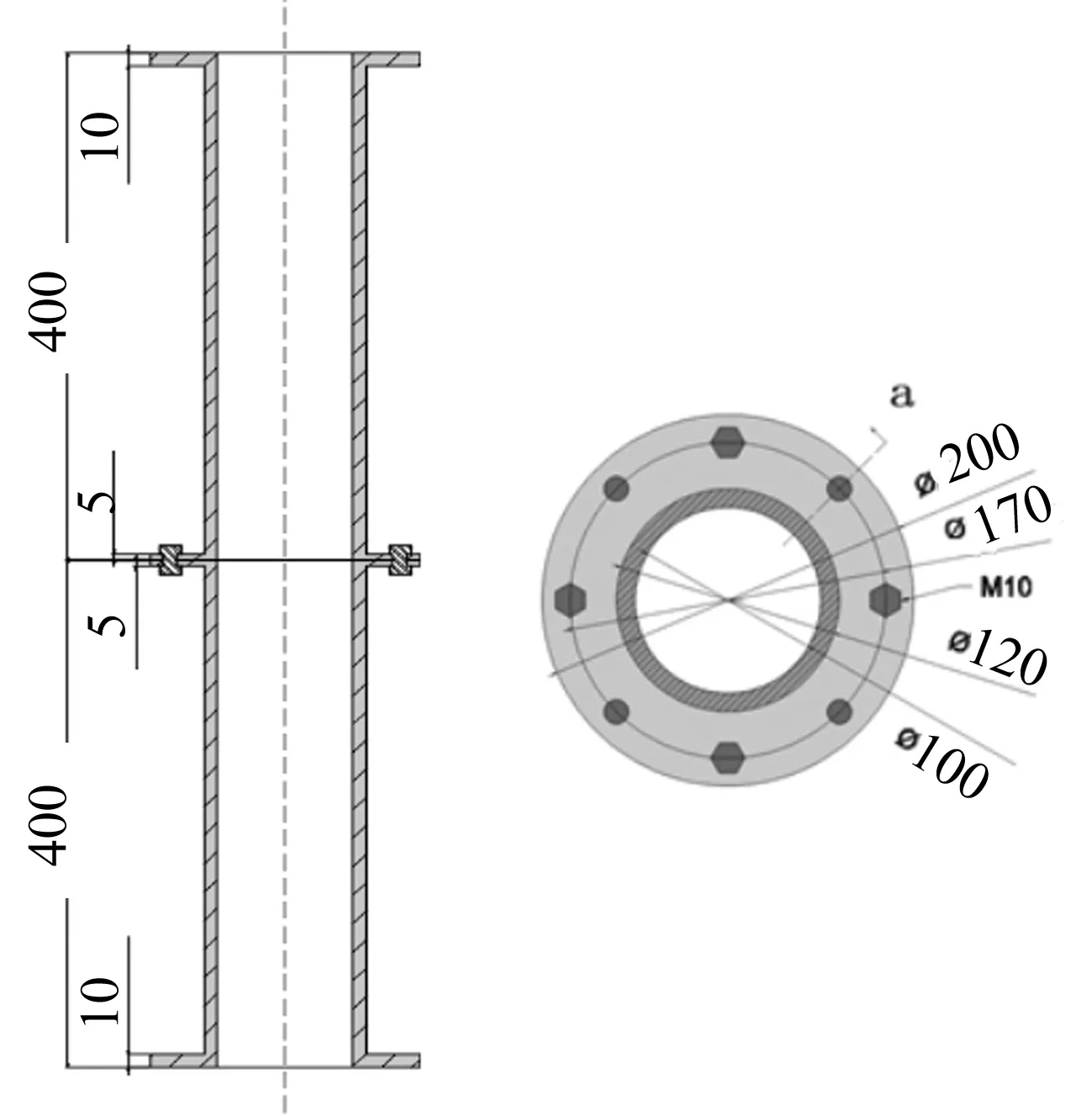
图1 螺栓法兰连接结构(mm)Fig.1 Bolted-flange assembled structure(mm)

(1)

式中：上标“*”表示由弹簧拉压状态决定其实际刚度；δ表示弹簧的拉压状态，受压为负，受拉或原始状态为正(图4)。系统内剪力销同样简化轴向拉压为双线性弹簧，不同的是弹簧的拉压状态，受压为负，受拉或不受力时为0。 剪力销弹簧由压缩刚度kp-确定，拉伸刚度由k0确定(图5(a))。

(2)

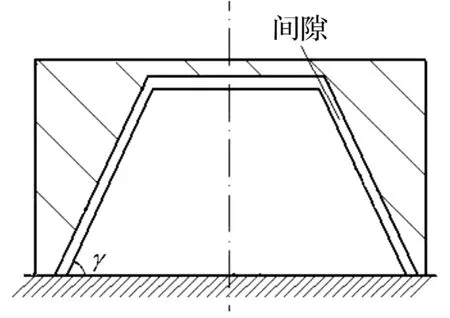
图2 剪力销受力过程Fig.2 The process of shear pin under force

图3 剪力销简化弹簧系统Fig.3 Simplified spring system of shear pin

图4 双线性弹簧Fig.4 Force-deflection curve for the bi-linear spring

特别的，系统装配间隙为ε时，其载荷位移曲线变为(图5(b))。

(3)

图5 双线性弹簧Fig.5 Force-deflection curve for the bi-linear spring

1.2 质量-拉压刚度不同系统

含剪力销(锥)螺栓法兰连接结构可以分为两个系统：螺栓-法兰系统、剪力销系统，其侧视图和剖面图如(图6)。

弯、剪、扭为螺栓-法兰连接典型的受力形式，为了结构的简化分析，现将(图5)结构抽象为抵抗弯、剪的三自由度质量-弹簧系统，以及抵抗扭转的二自由度质量-弹簧系统。下面分别对两种系统展开讨论。

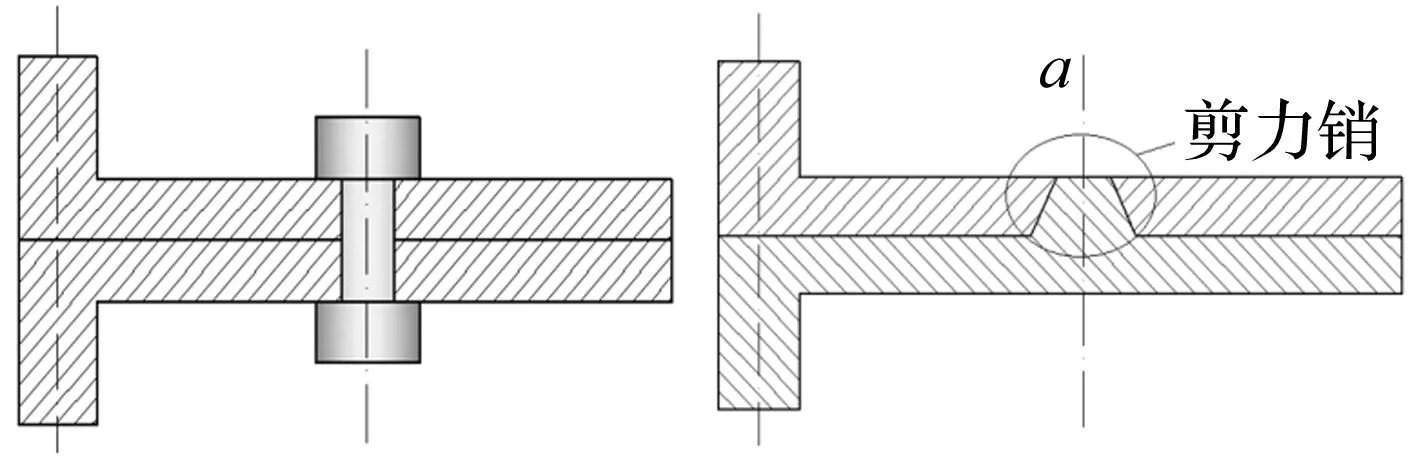
图6 剪力销与螺栓法兰连接结构示意Fig.6 Geometry of shear pin and bolted flange joint

1.2.1 横向冲击下三自由度系统

基于整体结构基本对称性(图1)，以连接部位接触面为对称面，取上半部分进行动力响应研究(图7)：

(1)上半部分连接的结构特性用相对O1点的质量m与转动惯量J表示；

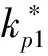
(4)以中心点O的位移u、v及转角θ分别描述系统的横向错动、轴向振动与弯曲振动。

由于双线性拉压不同刚度弹簧的引入，该系统可模拟结构轴向拉压不同刚度特性及轴向变形。在横向冲击作用时，剪力销弹簧可以模拟其抗剪特性，同时质量块m会产生面内转角。

在所建立的系统中，所有弹簧下端均固支，另一端与质量块相连。系统假设如下：①所有接触面均简化为无摩擦；②系统连接区域满足小变形；③连接处法兰盘为刚性平面，柱段也为刚性；④剪力销接触面受压时为线弹性小变形，且接触面受力均匀；⑤结构形心与质心重合于O1点；⑥受冲击作用时，弹簧只因自身轴向位移而产生作用，横向位移则对弹簧无影响；⑦系统轴向受压时，剪力销弹簧会产生微小恢复力，但其数量级远小于模拟螺栓弹簧的恢复力，因此忽略不计。

图7 三自由度质量-弹簧系统示意图Fig.7 The schematic of three degree freedom of mass-spring system

广义坐标δ下系统的无阻尼自由振动方程：

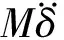
(4)

由刚体定轴转动时速度相互关系：

(5)

则系统动能表示为：

(6)

将式(5)代入式(6)中得：

(7)

由图7，根据O点位移与模拟两类弹簧连接点引起弹簧变形的转换关系为：

(8)

(9)

其中，δ1，δ2为左侧剪力销弹簧变形；δ3，δ4为右侧剪力销弹簧变形；δ5为左侧螺栓弹簧变形、δ6为右侧螺栓弹簧变形。由此可得，系统的弹性势能为：

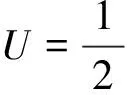
(10)

其中a为质量块高度，b为质量块宽度，r=a/2，α为剪力销弹簧倾角。

对于拉格朗日方程：

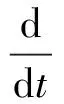
(11)

将系统动能式(7)，系统弹性势能式(10)代入拉格朗日方程，得出该三自由度质量—拉压双线性弹簧系统的无阻尼自由振动方程：

(12)

其中

通过式(12)的结构，可以得到如下推断：

1)方程中质量阵元素已知，为对称矩阵，且在横向与弯曲方向存在耦合项；

2)方程中刚度矩阵为满阵，三个自由度完全耦合，且由模拟螺栓与剪力销弹簧的拉压状态决定；

3)当α≠0°或α≠90°时，系统为全耦合状态，纵向、横向错动、弯曲三个自由度相互耦合。受弯、剪组合冲击时，该系统在三个自由度上会同时产生耦合振动；

4)方程解耦：

(1)当r=0，且α=0°或α=90°时。方程质量阵为对角矩阵，刚度阵为对称矩阵，横向与其它两个自由度解耦，仅纵向振动与弯曲振动耦合。

(2)当r=0，所有弹簧均为线性且刚度一致时，方程刚度阵、质量阵均变为对角阵，系统各自由度完全解耦。

(3)当系统初速度仅为轴向时，系统各自由度完全解耦。

1.2.2 扭转冲击下两自由度系统

为了描述扭转作用下螺栓-法兰连接的振动状态，同样基于对称性对上半部分进行分析(图8)。

图8 二自由度质量-弹簧系统Fig.8 Two degree freedom of mass-spring system

与三自由度系统不同的是，模拟两侧剪力销的1、2号弹簧，3、4号弹簧所在平面分别于质量块平面正交。中心点O的位移v及转角θ分别描述系统的轴向振动与扭转振动；在扭转冲击作用时，剪力销弹簧在表现为抗剪特性，由于倾角α的存在将力传递到轴向，使质量块m在其轴向产生扭转角θ。

系统的无阻尼自由振动方程：

(13)

由刚体定轴转动速度相互关系：

(14)

则系统动能表示为：

(15)

将式(14)代入式(15)中得：

(16)

根据O点位移与模拟剪力销弹簧及螺栓弹簧连接点的转换关系。

(17)

(18)

其中，δ1，δ2，δ3，δ4，δ5，δ6定义同上小节。b为质量块宽度，α为剪力销弹簧倾角。

所以，系统的弹性势能表示为：

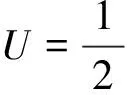
(19)

对于拉格朗日方程：

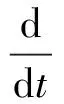
(20)

将系统动能式(15)，系统弹性势能式(19)代入拉格朗日方程，得出该三自由度质量-拉压双线性弹簧系统的无阻尼自由振动方程：

(21)

通过式(21)方程的结构，可以得到如下推断：

1)方程中质量阵元素已知，为对称矩阵；

2)方程中刚度矩阵为满阵，两个自由度完全耦合，且当α≠0°或α≠90°时，系统为全耦合状态纵向、扭转两个自由度相互耦合。

3)方程解耦：

(1)当α=0°时，方程刚度阵为对角矩阵，系统两个自由度解耦。

(2)当α=90°时，方程刚度阵为对称矩阵，系统两个自由度解耦。

(3)当系统初速度仅为轴向时，系统两自由度解耦。

2 计算模型验证

本文应用MATLAB建立计算模型，通过ODE求解器对模型进行动力学分析。相应动力学模型建立如下：

系统质量采用刚体表示其质量特性，刚体对O点转动惯量表示其惯性特性。当r=0且倾角α=0°，两侧剪力销模拟弹簧仅作为抗剪部件，对系统中轴向拉压无贡献(图9)。三自由度质量—弹簧系统中，刚体与螺栓弹簧连接，另外与两模拟剪力销弹簧相连接，所有弹簧另一端固支。O点分别释放平面内纵向、横向及z轴转向三个自由度。在系统刚体上加载绕z轴0.5 rad/s的初始转动速度，转动中心为O点，其它计算参数如(表1)。

图9 弹簧质量系统Fig.9 Mass-spring system

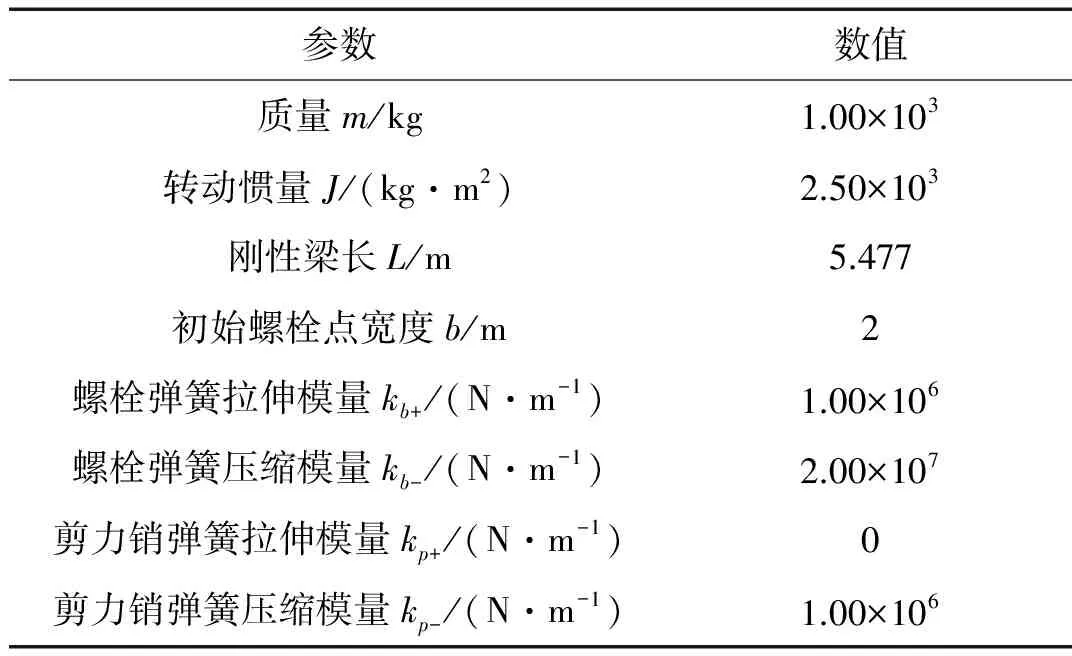
参数数值质量m/kg1．00×103转动惯量J/(kg·m2)2．50×103刚性梁长L/m5．477初始螺栓点宽度b/m2螺栓弹簧拉伸模量kb+/(N·m-1)1．00×106螺栓弹簧压缩模量kb-/(N·m-1)2．00×107剪力销弹簧拉伸模量kp+/(N·m-1)0剪力销弹簧压缩模量kp-/(N·m-1)1．00×106

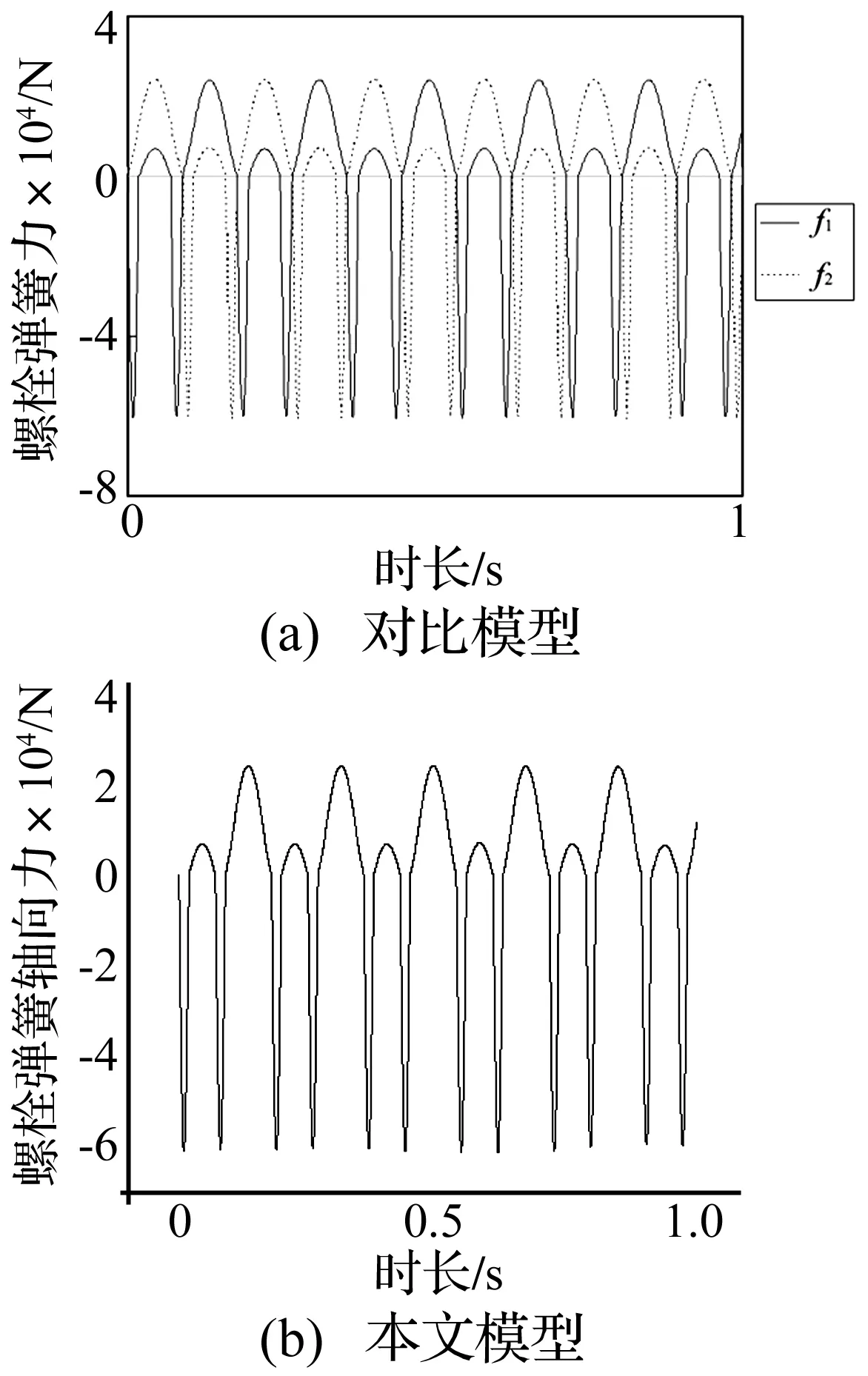
图10 螺栓弹簧力时程响应Fig.10 Time history response of spring force

由表2和图10可知，本文模型与栾[8]文中两自由度质量—弹簧精细模型的动力学特性一致。接下来本文重点分析剪力销倾角α，以及装配间隙对系统振动的影响。

表2 数值分析结果对比

3 含剪力销(锥)系统的振动特性分析

3.1 横向冲击作用下系统响应分析

本文1.2.1节中对横向冲击下三自由度系统机理阐述可知，α≠0°或α≠90°时，系统为全耦合状态。为了考量横向冲击下系统的振动状态，在三自由度系统中使r=0，此时系统排除了外载弯矩对振动状态的干扰，且仅受横向作用力，作用点为系统形心(图11)。

图11 形心处横向冲击模型Fig.11 Model of transverse impact on centroid

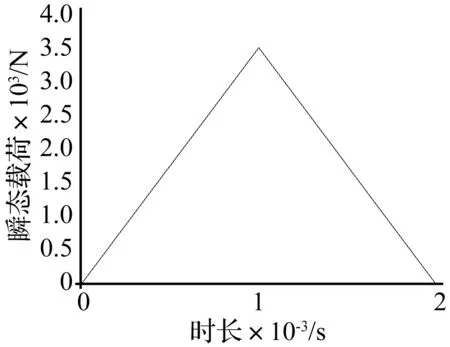
图12 横向冲击载荷Fig.12 Transverse impact

施加的作用力为横向瞬态冲击载荷，作用时长0.002 s内呈三角加载—卸载曲线(图12)，在0.001 s时达到峰值3 500 N，系统总运动时长为4 s。采集形心点处横向、纵向的时程—位移响应作为考察目标，通过快速傅里叶变换(FFT)获取响应频谱图(图13(a)、(b)、(c))。10°与20°时，纵向加速度低频存在干扰，且干扰接近横向频率，因此对两种角度下的频谱采用高通滤波。在30°时，纵向干扰频率出现在11～13 Hz，因此对该角度下频谱采用低通滤波排除干扰。从三个角度下的频谱分析可以看出，在横向冲击作用下，系统纵向振动频率为横向的2倍。

(a) α为10°横向与纵向位移频率响应 (b) α为20°横向与纵向位移频率响应 (c) α为30°横向与纵向位移频率响应图13 质量-弹簧系统形心处的冲击响应Fig.13 Vibration response on centroid of mass-spring system

3.2 扭转冲击作用下系统响应分析

由本文1.2.2节，对扭转冲击下两自由度系统机理阐述可知，当α≠0°或α≠90°，且冲击载荷为非轴向时，系统为全耦合状态，纵向、扭转两个自由度相互耦合。

3.3 螺栓最大拉力特性研究

由于含剪力销(锥)的螺栓法兰连接结构的非线性特性，其连接部段的几何突变及连续性缺失使得连接部段一直是该类结构设计所关心的重点。本文针对机理模型考查不同剪力销(锥)倾角，不同连接部段装配间隙对螺栓最大拉力的影响，得到不同参数下螺栓最大拉力分析图。

3.3.1 三自由度系统——螺栓最大拉力分析

剪力销(锥)在螺栓法兰连接结构中一直作为抗剪及改变冲击载荷传递方向的重要部件。具体分析中，当α≠0°或α≠90°，系统为全耦合状态，另使系统中r≠0，此时在刚体形心及两端中心点O、O1、O2施加同种横向瞬态冲击载荷(图7(a))。计算参数同上节，另a值为5.1 m，计算时长取T=4 s，输出结果步长为2.00×10-5s，系统为无摩擦假设。

对于作用点的不同，冲击力矩逐渐增大，在(表3)中给出0°、10°、20°、30°最大拉力及较初始状态的百分比结果。

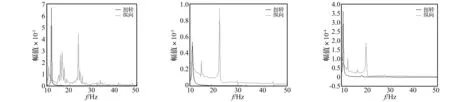
(a) α为10°纵向与扭转位移频率响应 (b) α为20°纵向与扭转位移频率响应 (c) α为30°纵向与扭转位移频率响应图14 质量-弹簧系统形心处的冲击响应Fig.14 Vibration response on centroid of mass-spring syste

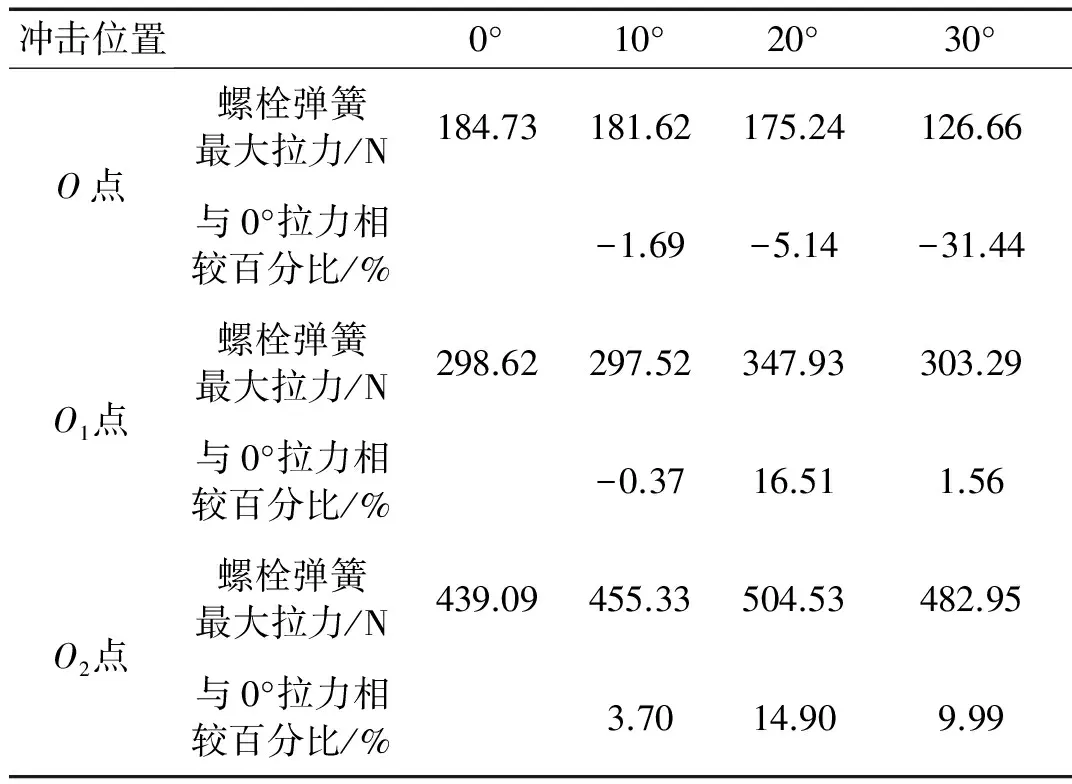
冲击位置0°10°20°30°O点螺栓弹簧最大拉力/N184．73181．62175．24126．66与0°拉力相较百分比/%-1．69-5．14-31．44O1点螺栓弹簧最大拉力/N298．62297．52347．93303．29与0°拉力相较百分比/%-0．3716．511．56O2点螺栓弹簧最大拉力/N439．09455．33504．53482．95与0°拉力相较百分比/%3．7014．909．99

由分析结果可以看出，系统在耦合状态下，剪力销(锥)随着其倾角变化对螺栓弹簧拉力贡献不同，主要体现在弹簧力-角度呈曲线状态(图15)。冲击作用在O点时，小角度范围内最大拉力普遍处于0°初值以下，并在30°时达到最小值。冲击作用在O1点时，0°～20°范围内最大拉力近似正弦曲线，在20°时达到最大值，增加幅值为16.51%。当作用力在O2点，力矩最大时，所得曲线形成螺栓弹簧最大拉力包络。在0°～20°范围内，虽然其变化幅度达到11.28%，但在15°时出现最小值。

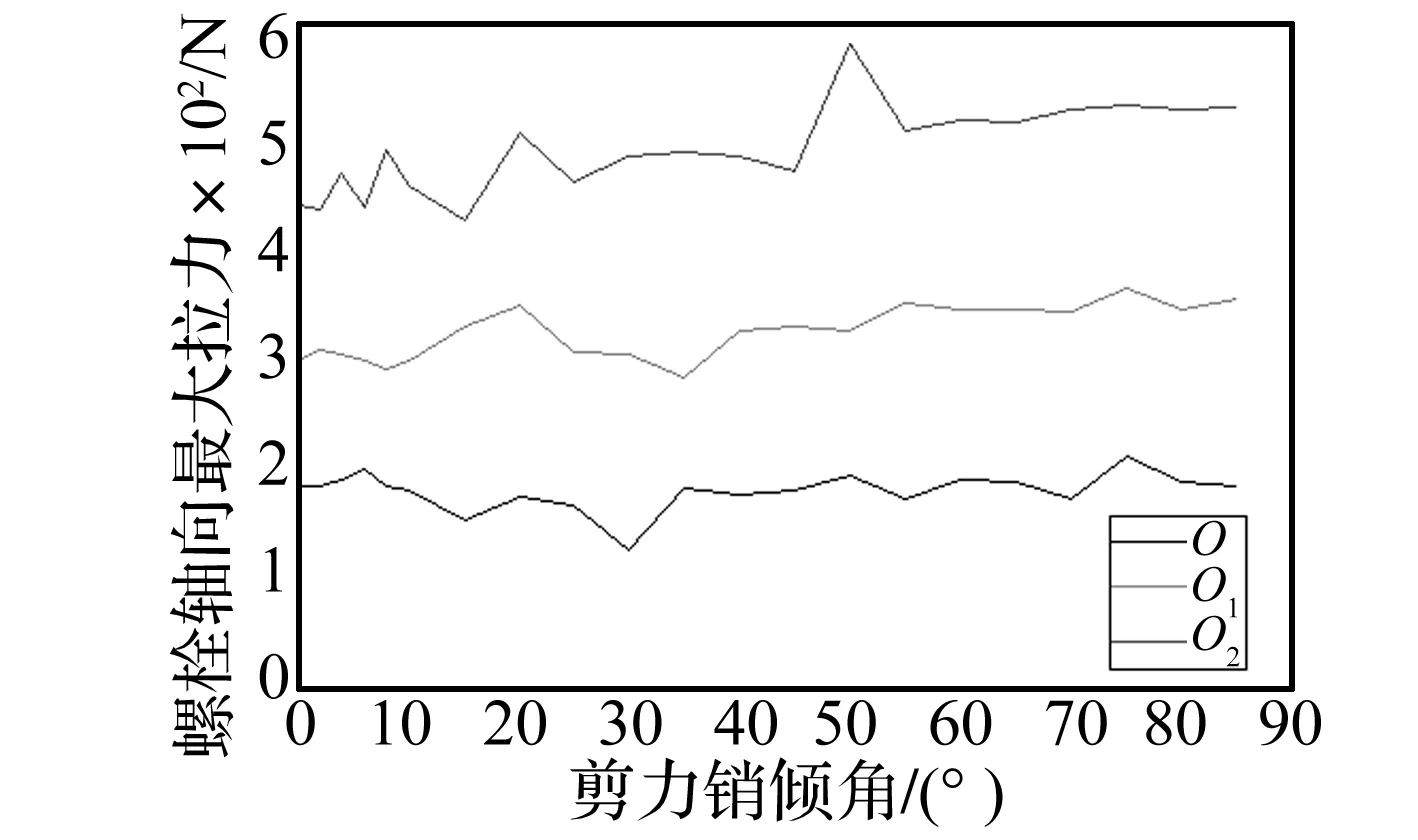
图15 螺栓弹簧力-角度曲线Fig.15 Curve of the spring force-angle

对于连接结构，影响其振动特性的又一动力学因素为装配间隙。实际结构中，装配间隙的存在往往加剧了结构非线性、接触非线性的影响。本文将此类问题转换为材料非线性，并结合剪力销(锥)倾角变化对螺栓最大拉力加以分析(图16)。在剪力销仅受抗剪作用时，0.2 mm为各间隙下拉力的最小值。结合倾角考虑，间隙在0.2 mm，剪力销倾角在16°时，拉力达到最小值371.73 N。并且各角度下，装配间隙为0.2 mm时，螺栓最大拉力相对较小，所以0°～20°范围为剪力销(锥)设计相对较好的角度区间。

图16 螺栓弹簧力-角度-间隙柱状图Fig.16 Histogram of the spring force-angle-clearance

3.3.2 两自由度系统——螺栓最大拉力分析

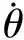
图17 螺栓弹簧力-角度曲线Fig.17 Curve of the spring force-angle

装配间隙与倾角变化综合考虑下(图18)，最大拉力值相较变化不大。在α=16°时，各间隙中0.2 mm与0.4 mm 螺栓所受最大拉力相对较小。0.2 mm间隙下最大拉力为2 231.9 N，0.4 mm间隙下最大拉力为2 191.6 N，两者相差2%以内。同时在受横向冲击时，间隙在0.2 mm时为最优。所以0.2 mm为较合理的装配间隙设计参考值。

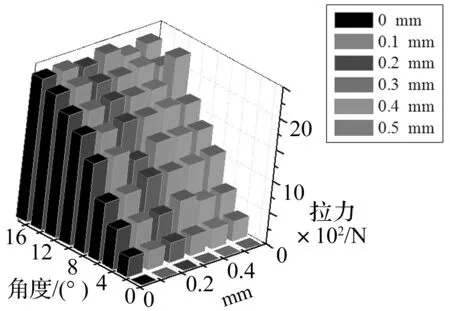
图18 螺栓弹簧力-角度-间隙柱状图Fig.18 Histogram of the spring force-angle-clearance

对横向冲击与扭转作用下系统螺栓弹簧最大拉力曲线进行归一化处理(图19)，在0°～40°范围内，扭转冲击下最大拉力增长率曲线一直处于横向冲击曲线下方，且小角度范围内相差较大。当α=50°时同时会达到峰值。在同量级横向冲击与扭转作用下，综合考虑剪力销设计角度，只要满足横向冲击设计即可。且随着连接件之间的磨损、腐蚀、外力撞击，会使接触部位倾角发生变化，因此20°并非理想设计方案。此时，0°～20°作为角度设计区间更加合理。

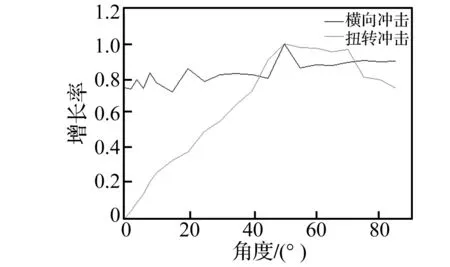
图19 最大拉力增长率-角度曲线Fig.19 Curve of the spring force growth rate-angle

4 结 论

为了对含剪力销(锥)的螺栓法兰连接结构进行振动特性分析，本文将接触非线性、结构非线性转化为材料非线性。基于此种转化，首先，对结构受力机理进行分析，提出转化模拟弹簧刚度曲线。其次，建立两种自由度质量-弹簧系统非线性动力学模型，通过其数学列式讨论了相关参数对耦合的影响，并编写程序对数值、图像校验模型正确性。再次，对两种自由度系统施加冲击载荷，观察相应的系统频域响应，发现对应的倍频关系。最后，探讨了剪力销(锥)倾角变化对螺栓最大拉力的影响，并得到两种机理模型的最大拉力包络线，在此基础上，本文引入装备间隙，根据柱状图像得出最佳剪力销(锥)倾角设计区间及相应的装配间隙。

[1] 卫洪涛，孔宪仁，王本利，等. 基于振型转换的螺栓连接梁非线性振动研究[J]. 振动与冲击，2014，12(33)：42-47. WEI Hongtao ，KONG Xianren，WANG Benli，et al.Non-linear dynamic response of a beam with bolted joint based on modal shape transfer[J].Journal of Vibration and Shock，2014，12(33)：42-47.

[2] 郑晓亚，徐超，王焘，等. 螺栓-法兰连接结构非线性优化设计方法研究综述[J]. 强度与环境，2008，3(1)：7-13. ZHENG Xiaoya，XU Chao，WANG Tao，et al. Study on nonlinear optimization design for bolted flanged connection[J]. Structure & Environment Engineering，2008，3(1)：7-13.

[3] KATNAM K B， DA SILVA L F M， YOUNG T M. Bonded repair of composite aircraft structures: a review of scientific challenges and opportunities[J]. Progress in Aerospace Sciences， 2013， 42： 26-42.

[4] FUKUOKA T,TAKAKI T. Elasto-plastic analysis of bolted joint during tightening process[J]. Transactions of the Japan Society of Mechanical Engineers: A,2001,67(660) ：1269-1275.

[5] ZHAO Hua. Stress concentration factors within bolt-nut connectors under elasto-plastic deformation [J]. International Journal of Fatigue，1998，20(9)：651-659.

[6] 杨敏. 螺栓连接结构的一种简化数值模拟方法[J]. 机械设计与制造，2012(7)：165-167. YANG min. A simplified numerical simulation approaches for bolted joint connections[J]. Machinery Design & Manufacture，2012(7)：165-167.

[7] 陈长盛,王强,柳瑞锋,等.螺栓连接对结构模态及传递特性影响研究[J].振动与冲击,2014,33 (2):178-182. CHEN Changsheng，WANG Qiang，LIU Ruifeng，et al.Effect of bolt connection on structural vibration modes and transfer characteristics[J]. Journal of Vibration and Shock，2014，33(2):178-182.

[8] LUAN Yu， GUAN Zhenqun， CHENG Gengdong， et al. A simplified nonlinear dynamic model for the analysis of pipe structures with bolted flange joints[J]. Journal of Sound and Vibration， 2012,331(2)：325-344.

[9] 石永久，潘斌，施刚，等.高强度钢材螺栓连接抗剪性能试验研究[J]. 工业建筑，2012，42(1) ：56-61. SHI Yongjiu，PAN Bin，SHI Gang，et al. Experimental study on high strength steel-plate-bolted connections under shear force[J]. Industrial Construction，2012，42(1) ：56-61.

[10] 杨东升，胡伟平，吕来清. 销钉耳片连接件接触应力分析的能量解法[J]. 应用力学学报，2011, 28(3)：304-308. YANG Dongsheng，HU Weiping，LÜ Laiqing. The energy approach to contact stress analysis of pinned connections[J]. Chinese Journal of Applied Mechanics，2011,28(3) ：304-308.

[11] 施永恒. 高速铁路空间刚架结构剪力销疲劳性能研究[D]. 成都:西南交通大学，2012.

[12] CHEN Qiuren，GUO Haiding， ZHANG Chao，et al. Structural optimization of the uniaxial symmetry non-circular bolt clearance hole on the turbine disk[J].Chinese Journal of Aeronautics, 2014, 27(5): 1142-1148

[13] KIRAL B G. Effect of the clearance and interference-fit on failure of the pin-loaded composites[J]. Materials & Design，2010，31(1)： 85-93.

[14] 王花娟，杨杰，刘新东，等. 装配间隙对GF/E螺栓连接强度的影响[J]. 宇航材料工艺，2008，38(1)：78-80. WANG Huajuan，YANG Jie，LIU Xindong，et al. Fit-up gap effect on bolted joints strength of twill GF/E composites[J]. Aerospace Materials & Technology，2008，38(1)：78-80.

[15] CHOWDHURY M A, HELALI M M. The effect of frequency of vibration and humidity on the coefficient of friction[J]. Tribology International, 2006,39: 958-962.

[16] CHOWDHURY M A, HELALI M M. The effect of amplitude of vibration on the coefficient of friction different materials[J].Tribology International, 2008,41: 307-314.

Coupled vibration of bolted flange connections containing shear pins (cone)

LU Xu, ZHANG Yuhang, CHEN Yan, MAO Pengcheng, YU Fei, GUAN Zhenqun

(State Key Laboratory of Structural Analysis for Industrial Equipment/Department of Engineering Mechanics, Dalian University of Technology, Dalian 116024, China)

Under complex and multiple external loads, the coupled vibrations of joint structures in large industrial equipments were analysed. Two schematic nonlinear dynamic models with multi DOFs were developed to study the dynamics mechanism of bolted flange joints containing shear pins (cone) subjected to the combined action of bending moment, shearing force and torsion moment. The vibration behavior and coupling relationship under the combined loading were discussed. On this basis, the effects of cone angle and assembly clearance on the maximal axial tensile force on the bolts were investigated to give the most appropriate angle design region and the corresponding assembly clearance range.

joint structure; shear pin (cone); nonlinearity; coupled vibration; assembly clearance

国家自然科学基金(10872040;11272074)；国家科技重大专项(2011ZX02403)

2015-06-18 修改稿收到日期：2016-01-06

芦旭 男，博士生，1982年生

关振群 男，硕士，教授，1965年生

V414.1

A

10.13465/j.cnki.jvs.2017.02.023