单面瓦楞机光辊机构动力学分析

尚 雯, 杜群贵

(华南理工大学 机械与汽车工程学院，广州 510640)

单面瓦楞机光辊机构动力学分析

尚 雯, 杜群贵

(华南理工大学 机械与汽车工程学院，广州 510640)

单面瓦楞机在成型的过程中存在较大的振动，为了分析振动的原因及减振，对单面瓦楞机的关键机构——光辊机构进行动力学建模，发现推杆刚度不足，造成光辊机构的非线性。进行振动测试，验证了动力学模型的正确性，得到单面瓦楞机振动的主要原因：单面瓦楞机在正常工作转速范围内，存在两个共振频率。最后对光辊机构提出改进方案，并仿真对比改进前后光辊机构在受迫振动下的振动位移，改进后的位移幅值降低了35.2%。研究结果为降低瓦楞机的振动提供了理论依据。

瓦楞机；光辊机构；动力学建模；振动测试

单面瓦楞机是瓦楞纸板生产线上关键的机器。光辊(又叫压纸辊)是单面瓦楞机中的三大辊子之一，其主要作用是将面纸与已经成瓦楞型的芯纸粘合。随着瓦楞机械和瓦楞机生产线的高速化发展[1]，以及对生产纸板宽度要求的增加，瓦楞机的机型在不断改进。在改进的过程中瓦楞机会出现较大的振动，但是目前很少有学者对光辊机构进行单独的动力学研究。

在瓦楞辊工作的过程中，由于啮合方式不同于齿轮，每次只有一个齿啮合，上、下瓦楞辊成型纸张时中心距是变化的，这也是冲击存在的原因[2]。光辊与上瓦楞辊的啮合是齿线与面的接触，光辊在气缸压力下会保持与上瓦楞辊的压紧，因此运动时会产生定量的中心距变动[3]。实际上，光辊与上瓦楞辊中心距的变动大小是随着转速变化而变化的，据分析见文中第2节。

引起单面瓦楞机的振动原因很多，光辊的冲击是其振动的主要原因之一。本文主要是为了研究某型号单面瓦楞机光辊机构的运动对瓦楞机振动的影响，并且对光辊机构进行优化。

1 光辊机构动力学建模

瓦楞机三维模型的左视图如图1所示。图中:4为光辊机构中的光辊，由于光辊较长，可以被简化为简支梁，故可以考虑建立其完整的动力学模型，如图2所示为光辊机构三维模型平面化的视图。

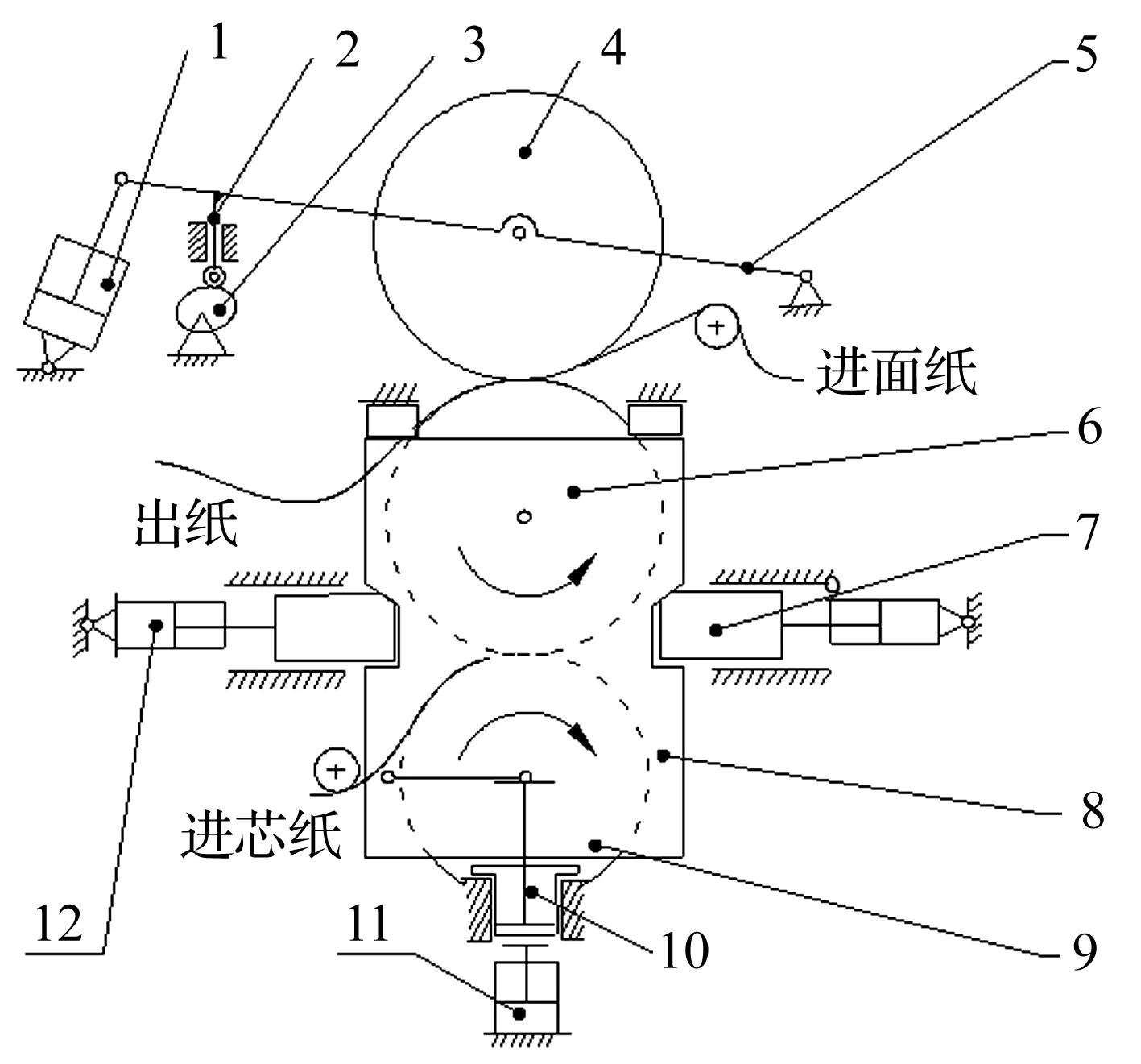
1-气缸，2-限位杆，3-凸轮，4-光辊，5-光辊支架，6-上瓦楞辊，7-油缸，8-卡闸机架，9-下瓦楞辊，10-油缸，11-油缸12-油缸 图1 瓦楞机装配原理图Fig.1 The assemble theory graph of corrugating machine

1、6-光辊支架，2、5-限位杆，3、4-气缸，7-光辊图2 光辊机构的简化模型Fig.2 The simplified model of pressure roller mechanism

上瓦楞辊是主动辊，其与下瓦楞辊啮合的过程中将芯纸成型为带瓦楞的芯纸，之后上瓦楞辊带着芯纸与光辊带着的面纸进行粘合形成单面瓦楞纸。

由图1中的构件1～5组成光辊机构完整模型如图2所示，光辊7由光辊支架铰接，可以看作简支梁。图中：光辊7的质量M及其转动惯量J2；光辊支架1和6质量m及转动惯量J1;油缸3和4的弹簧等效刚度K1；限位杆2和5的弹簧等效刚度K2;l1为光辊到铰接点的长度；l2为光辊支架质心到铰接点的长度；l3为限位杆到铰接点的长度；l4为气缸到铰接点的长度。

由图2(a)转化到图2(b)时，将油缸3和4等效为刚度K1的弹簧，而限位杆可以等效为刚度K2的弹簧。

图2(b)中所建模型具有两个自由度，分别是两个光辊支架的转角θ1、θ2，当瓦楞机工作的时候，上瓦楞辊带着已经成型的涂着均匀浆糊的芯纸与光辊带着的面纸相互粘合、贴紧，在此过程中光辊与上瓦楞辊没有直接接触，中间隔着芯纸、浆糊、面纸。粘合的压力F要控制好，F过大，则纸张会被压烂；F过小，则不能使芯纸与面纸很好的粘合在一起。F的大小是由限位杆和油缸共同决定的，其中限位杆与光棍机构是通过螺纹连接的，可以通过凸轮调整限位杆位置，防止纸张被压烂，达到调整F的目的。

当瓦楞机正常工作时，与图2(a)所示限位杆接触的凸轮已经被完全固定的(不可以转动)，此时将凸轮看作一个支撑点即可，由于光辊与上瓦楞辊之间有中心距的变化，所以当θ1>0时，限位杆2刚度K2=0，此时限位杆与凸轮脱离；当θ1>0时，限位杆2刚度K2≠0，此时限位杆与凸轮接触。同理限位杆5的刚度变化也是如此。由于限位杆刚度K2是非线性变化，光辊机构动力学模型的求解变为非线性问题。阻尼C难以确定且其对固有频率的影响较小，为简化计算将其忽略。对于刚度K2分两步研究，第一步按定值处理，后续再考虑其非线性因素。

研究机构的动力学特性，首先要研究其固有频率及阵型，当激励频率等于固有频率时，会有共振发生，所以设计及修改机构时要避开共振区。

本节首先计算光辊机构自由振动的固有频率和阵型，之后再讨论其受迫振动的情况。

对简化的模型运用拉格朗日函数列方程。

设Qi为与广义坐标qi(i=1,2,3，…，n)相对应的非保守力，L=T-V(T为动能，V为势能)，由拉格朗日函数，拉格朗日第二类方程[4]的一般形式为：

(1)

下面计算光辊机构的固有频率，其中qi对应于θ1与θ2，Qi=0；

对光辊7计算动能T，由两部分组成，一部分是光辊质心平动的动能，另一部分是光辊绕质心转动的动能：

对光辊支架1列T和V(势能)：

对光辊支架6列T和V：

将以上计算得到的T和V代入式L=T-V和式(1)得到标准方程：

(2)

其中

以下是某型号瓦楞机的参数的具体值：

M=1 139.4 kg；J1=8.25 kg·m2；J2=584.47 kg·m2；

m=135 kg；K1=159 947.2 N/m；K2=45 560 N/m；

l1=368.787 mm；l2=385.947 mm；

l3=652.24 mm；l4=798.46 mm。

代入方程，求解得

然后将ωn1=10.75，ωn2=23.47分别代入式(4)计算得到阵型依次为：

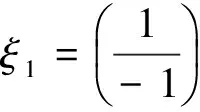
非线性模型的求解过程比较复杂，有以下几种方法：正规摄动法、多尺度法和线性平均法等。

结合本文光辊机构的模型，第三种线性平均法是最简便的方法，模型中非线性的因素是K2，所以在计算非线性模型时，只需要将刚度矩阵线性化，质量矩阵不变，方程形式同式(2)。

在不考虑图2～4中2-限位杆材料非线性的情况时，刚度矩阵中的K2，由于角位移而导致的刚度非线性[5-9]如下所示：

其中xe等于图2(a)中2-限位杆的预压缩量，为便于后续对刚度进行线性化计算，令振动角位移x=Acos(φ)，其中A为幅值，φ对应于限位杆变形得到的角度与图2(b)中弹簧变形量有关的值，刚度K2可表示为

(3)

由式(3)可知当φe=0，光辊机构自身的非线性因素就会消失，即K2转化为常量。所以精确确定瓦楞机正常工作时的限位杆初始变形量是很有必要的，上面的参数xe是一个近似值，通过测试可以找到精确值。

线性化过程如下：

由线性平均法一个周期内将K11线性化

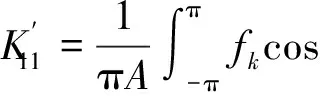
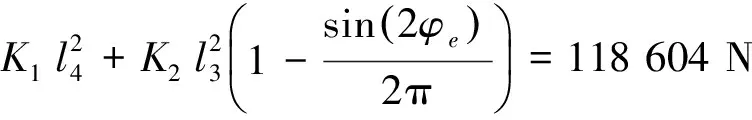
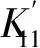
式(2)转化为

(4)

解得：

与前面用线性的方法求得的固有频率相比，一阶、二阶固有频率均有略微减小，阵型是一致的。而且随着φe值的变化，K11会发生变化，固有频率也会有变化。当φe接近零时，非线性的解就会逐步接近线性解。

2 振动测试

为了验证前文中所建立模型的可行性，对该型瓦楞机整机进行振动测试实验，由于本文只关注光辊机构的振动情况，所以重点研究光辊支架上的加速度传感器测得的信号。振动测试所用仪器为东华振动测试仪DH5922N及其配套振动加速度传感器和一个光电转速传感器。

加速度传感器安装在光辊支架上，光电转速传感器直接测量下瓦楞辊的转速。由于测试现场环境的限制，啮合频率(由下瓦楞辊转速转化得到)每增加20 Hz，在该频率下采样10 s左右，采样频率5 120 Hz，所以测试结果中的振动峰值处的频率会有一定的误差。

图3 光辊与上瓦楞辊一个周期啮合的过程Fig.3 The mesh process of the pressure roller and the top corrugated roller in a mesh circle

图3中做出了随着上瓦楞辊转动，光辊与其啮合的过程，当圆频率ω很小的时候，会有两个上瓦楞辊的辊齿同时与光辊接触；当ω逐渐增大到一个临界值ω0后，会出现只有一个齿接触的情况，即图3中ωt=0时的状态，ω0的取值与光辊机构所连接的油缸的响应速度有关，由此可以得出，光辊与上瓦楞辊的中心距的变动大小是随着转速变化而变化的，当达到转速取ω0，中心距几乎不再变化。

依据振动测试数据作图4，其横坐标为光辊与上瓦楞辊的啮合频率，由下瓦楞辊转速转化而来，纵坐标为光辊机构加速度峰峰值，该值为在某啮合频率下测试的最大值幅值，因此图4可以看作是光辊机构振动的幅值图。

图4 振动测试加速度峰峰值图Fig.4 Peak-to-peak value graph of the acceleration of vibration test

由图4可知，峰峰值随着转速增大先增大，再减小，可验证前面提到的中心距在到啮合频率达临界值ω0时就不再变化。因此可以判断光辊机构在啮合频率为217 Hz左右时出现共振。为了分析共振的原因，在啮合频率为217 Hz时，对此时采集的加速度信号进行傅里叶变换(FFT)、细化分析[10]以及Hilbert解调分析如图5。

图5 加速度信号频谱分析Fig.5 The spectral analysis of the acceleration signal

图5所示的FFT变换分析采样分析点数为40 539个点，细化的中心频率在217 Hz，细化倍数50倍，频谱的细化可以得到更加精确的共振频率和调制频率对应的幅值，图5中细化频率216.3 Hz处的峰值比未细化时的峰值要精确一些。而Hilbert变换可以提取精确的调制频率。

由光电转速传感器间接得到的啮合频率217 Hz与振动加速度频谱分析得到的基频216.3 Hz基本一致，由此可以得出瓦楞辊的啮合是光辊振动的振源。

从振动加速度信号中发现啮合频率周围存在对称分布的变频带，由此可以判断光辊振动中存在幅值调制[11-12]，调制频率为1.64 Hz，经过分析发现该调制信号来自下瓦楞辊的转频，而下瓦楞辊与光辊并不直接接触，所以光辊振动的调制频率应该是由上瓦楞辊传上来的，其与上瓦楞辊和光辊之间的啮合频率叠加，得到振动测试中的信号成分。而这个调制频率与上一节建立的光辊机构非线性动力学模型的一阶固有频率1.69 Hz非常接近，可以断定光辊机构在激振频率为1.64 Hz左右(因为测试频率间隔较大所致)的时候出现共振，同时也说明非线性的模型计算得到的结果更为准确。

3 对光辊机构的改进方案

3.1 改进方案的提出

光辊的改进可以有两种方案，方案一：将限位杆改为油缸以实现限位的作用，为了控制面纸与芯纸之间的粘合力F，还需要采用控制阀对两个油缸的流量或者压力进行控制，此方案成本高、复杂，如果使用得当会有很好的减振效果；方案二：在限位杆与凸轮接触的位置安装减振器，这个方案简单，成本低，需要配合较高的工艺和装配，才能使限位杆处消除冲击。

综合考虑，本文采用方案二，在限位杆处安装减振器会直接改变限位杆处的刚度K2的值，在MATLAB中作出光辊机构固有频率随着K2变化而变化图。

由图6曲线可以看出，随着刚度K2增大，光辊机构的一阶和二阶固有频率不断增大，理论上可以通过增大或者减小光辊机构的固有频率避开瓦楞机正常工作时的频率。如果考虑通过减小光辊机构的固有频率来使其二阶固有频率小于瓦楞辊(调制频率的来源)的转频，由图6可知，这会使K2的值过小而导致光辊机构的运动位移增大，不利于系统的稳定，说明减小光辊固有频率是不可行的。所以本文考虑通过增加光辊机构的固有频率来达到要求。

图6 光辊机构固有频率随着K2变化图Fig.6 The natural frequencies of the pressure roller mechanism vary with the value of K2

要增大固有频率即增加K2的值，只需要增加限位杆的直径，这在生产上是简单易完成的。

瓦楞机正常工作时瓦楞辊的转频(振动测试时的调制频率)比较接近光辊机构的频率，虽然现在瓦楞机朝着高速化的方向发展，但是考虑到该型号瓦楞机的线速度目前还达不到400 m/min(其对应瓦楞辊的转频为6.5 Hz)所以本文通过增大K2至3.88×106N/m以增加光辊机构自身的固有频率使其大于瓦楞辊工作时的转频，以此来改善瓦楞机振动状况。结果对比如表1所示。

表1 光辊固有频率对应刚度K2表

3.2 改进前后仿真计算对比

为了对比光辊机构改进前后仿真计算振动的结果，首先找一组实验数据作为参照，依据该位移倒推出光辊振动过程的激励力。

实际工况下，瓦楞机最常见的线速度为150 m/min，对应的下瓦楞辊转频为2.45 Hz，提取此时的光辊振动位移信号如图7所示。

图7 提取振动测试中的调制信号Fig.7 Modulation signal extracts from the vibration test

由图7可得其位移的最大值为0.014 mm，以此作为参考，对比光辊在刚度K2改变前后，在相同的受迫力F(t)下，其稳态位移的改善情况。

由图7中振动加速度的测试数据提取的粗实线可以看出在时域上位移存在明显的幅值调制，受迫力F(t)随着光辊与上瓦楞辊中心距的变动出现浮动，上瓦楞辊对光辊的激励信号由啮合频率及其倍频与下瓦楞辊的转频叠加形成的。

因此假设力F(t)按照三角函数的规律变化，令

F(t)=

其中，ω1=2π×2.45 rad/s为调制圆频率，ω2=132ω1(132为齿数)为载波圆频率。取F(t)>0的部分如图8，F(t)是均布力，仿真时设置的采样频率也是5 120 Hz，可以等价为直接在光辊轴两端的光辊支架上对应位置施加F(t)/2的力，由于粘合力大小不能精确计算，取一个近似值F0=3 688 N。

图8 力F-t图Fig.8 The graph of force F to time

同理由拉格朗日函数(1)列方程得

其中力矩M(t)=F(t)×l1，F(t)可以由谐波分析法(傅里叶级数)转化一系列谐波的叠加，F(t)的常量产生的位移可以通过平移消除，所以这里不考虑常量的影响。由第2节可知，该系统可以转化为线性系统，可用叠加法，即分别求得各个分量对应的稳态响应x1，x2，x3，x4，……,之后将这些稳态响应叠加得到稳态振动位移x。

在MATLAB进行求解，分别令K2=4.56×105N/m和3.88×106N/m进行计算得到位移x如表2。

表2 位移随着K2变化表

振动测试得到的位移与未改进时仿真计算的结果较为接近，说明仿真计算中用到的力F(t)是较为准确的，对刚度比改进前后的位移，发现最大位移减少了35.2%，说明可以起到一定的减振作用。由图6知K2越大，则光辊机构的固有频率越大，即远离激振频率。由此可见K2在一定范围内是越大越好，由于限位杆的尺寸限制，K2只需满足要求即可。

4 结 论

由于限位杆可能有非线性存在，本文分别建立线性和非线性光辊机构的动力学模型，前者计算得到的光辊机构的固有频率略大于后者的计算结果，在一定条件下非线性可以转化为线性。振动测试实验得到的共振频率与动力学模型计算的结果是一致的，说明该模型是可行的。

最后又根据该模型对光辊机构提出了改进的措施，通过增大限位杆的刚度K2将光辊机构的固有频率提高到6.5 Hz以上，避开下瓦楞辊转频(调制频率)的频率范围，并仿真计算光辊机构在刚度K2改变前后的受迫振动位移的变化，对比发现改进后的机构振动位移降低，对降低单面瓦楞机的振动起到积极的作用。

[1] 刘丕群. 瓦楞纸板生产线运动学和动力学仿真[D]. 广州: 华南理工大学, 2013.

[2] 柯晖，周世棠,葛峰，等. 高速瓦楞辊机构的中心距方程及其运动分析[J]. 湖北工学院学报, 2001,16(1): 48-51. KE Hui，ZHOU Shitang，GE Feng,et al. Synthesis of the center’s distance of high-speed corrugating roller[J]. Journal of Hubei Polytechnic University,2001，16(1)：49-51.

[3] 熊桂超，杜群贵. 单面瓦楞机的瓦楞辊机构中心距变动方程[J]. 科学技术与工程, 2011,11(22): 5290-5294. XIONG Guichao，DU Qungui. The equation of the changing center of single-sided corrugating machine corrugating roller[J]. Science Technology and Engineering, 2011，11(22)：5290-5294.

[4] 刘延柱. 振动力学[M]. 北京: 高等教育出版社, 1998.

[5] 王立华，李润方，林腾蛟,等. 齿轮系统时变刚度和间隙非线性振动特性研究[J]. 中国机械工程, 2003，14(13): 1143-1146. WANG Lihua，LI Runfang，LIN Tengjiao，et al. Research on nonlinear vibration characterisitcs due to time-varing mesh stiffness and gear backlash in gear system[J]. China Mechanical Engineering, 2003, 14(13): 1143-1146.

[6] 刘北辰. 多自由度非线性动力方程求解的新方法[J]. 昆明工学院学报,1994，19(6): 64-72. LIU Beichen. A new methods for the solution to multivariate nonlinear dynamic equations[J]. Journal of Kunming Institute of Technology, 1994，19(6): 64-72.

[7] 刘国华，李亮玉，李培明,等. 含间隙和时变刚度的齿轮系统非线性动力学模型的研究[J]. 机械设计,2008，25(5): 27-30. LIU Guohua，LI Liangyu，LI Peiming, et al. Study on nonlinear dynamics model of the gear system with clearance and time varying stiffness [J]. Journal of Machine Design, 2008，25(5): 27-30.

[8] 卢绪祥，刘正强，黄树红,等. 含间隙碰撞振动系统的非线性振动特性[J]. 动力工程学报,2012，32(5): 388-393. LU Xuxiang，LIU Zhengqiang，HUANG Shuhong，et al. Nonlinear vibration characteristics of a vibro-impact system with clearance [J]. Journal of Chinese Society of Power Engineering,2012，32(5): 388-393.

[9] 王常峰，陈兴冲，朱春林,等. 考虑支座及限位装置非线性的接触摩擦单元模型[J]. 工程力学, 2013，30(8): 186-192. WANG Changfeng，CHEN Xingchong，ZHU Chunlin，et al. The contact and friction element considering nonlinear performance of movable supports and restrainers [J]. Engineering Mechanics,2013，30(8): 186-192.

[10] 丁康，潘成灏，李巍华. ZFFT与Chirp-Z变换细化选带的频谱分析对比[J]. 振动与冲击,2006，25(6): 9-12. DING Kang，PAN Chenghao，LI Weihua. Spectrum analysis comparison between ZFFT and Chirp-Z transform [J]. Journal of Vibration and Shock,2006，25(6): 9-12.

[11] 周福昌，陈进，何俊,等. 循环平稳信号处理在机械设备故障诊断中的应用综述[J]. 振动与冲击, 2006，25(5): 148-152. ZHOU Fuchang，CHEN Jin，HE Jun，et al. Survey of the application of cyclostationary signal processing in machinery fault diagnosis [J]. Journal of Vibration and Shock,2006，25(5): 148-152.

[12] 丁康，孔正国，李巍华. 振动调频信号的循环平稳解调原理与实现方法[J]. 振动与冲击,2006, 25(1): 5-9. DING Kang，KONG Zhengguo，LI Weihua. Principle and method of cyclostationary analysis for demodulating frequency modulated vibration signal [J]. Journal of Vibration and Shock,2006, 25(1): 5-9.

Dynamic analysis on the pressure roller mechanism of the single-sided corrugating machine

SHANG Wen, DU Qungui

(School of Mechanical and Automative Engineering, South China University of Technology, Guangzhou 510640, China)

In the process of paper forming, serious vibration is usually existing in a single-sided corrugating machine. In order to analyze the causes of vibration and thus reduce it, a dynamic model was set up to study the key mechanism of the single-sided corrugating machine—the pressure roller mechanism. The simulation results show that it is the insufficient stiffness of the push bar which causes the nonlinearity of the pressure roller mechanism. An additional experiment was carried out to verify the validity of the dynamic model, from which the main reason resulting in the vibration of the machine was revealed. It turns out that the single-sided corrugating machine has two resonance frequencies when it works within the normal rotating speed range. Finally, an improvement solution was proposed to control and reduce the vibration by increasing the stiffness of the push bar. Simulation comparisons show that the forced displacement of the mechanism is reduced by 35.2 percent using the improvement solution, which provides a theoretical reference for reducing the vibrations of corrugating machines.

corrugating machine; pressure roller mechanism; dynamics model; vibration test

广东省省部产学研项目(2012B091000140);广东省省级科技计划项目(2013B010203016)

2015-08-13 修改稿收到日期：2015-12-31

尚雯 男，硕士生，1989年12月生

杜群贵 男，博士，教授,博士生导师，1965年6月生 E-mail：ctqgdu@scut.edu.cn

TH132.4

A

10.13465/j.cnki.jvs.2017.02.012