双变激振超细振动磨电机驱动转速多工况组合优选研究

高 远, 贾民平, 杨小兰, 刘极峰

(1.东南大学 机械工程学院，南京 211189； 2.南京工程学院 机械工程学院，南京 211167)

双变激振超细振动磨电机驱动转速多工况组合优选研究

高 远1, 贾民平1, 杨小兰2, 刘极峰2

(1.东南大学 机械工程学院，南京 211189； 2.南京工程学院 机械工程学院，南京 211167)

针对恒速振动电机振动磨在超细粉碎过程中易出现物料团聚而引起颗粒细化难度增大、超微粉碎发展受限的情况，提出振动电机转速、激振偏心块矢径随时间变化的双变激振方式，结合Adams仿真及样机试验对电机转速变化曲线进行优化,从而实现了对高振强特性超微粉碎激励方法的研究。通过模拟分析振动磨机不同转速工况下的运动响应特性、振强变化规律，对电机转速最佳变化范围和组合效应进行研究，以平均粒径为10 μm的金刚石粉末为研磨对象进行120 h新型振动磨机的碎磨试验，从而验证了组合优选所得到的电机转速变化曲线能够使得颗粒进一步细化。

振动磨；超细粉碎；电机转速；高振强

纳米级的超硬材料不仅硬度高、抗磨损性能好，还具备特殊的物理化学特性，具有极为广阔的应用前景。近几年来，工业生产广泛采用机械粉碎法制备纳米颗粒，该方法具有成本低、易规模化等优势。振动磨[1-2]作为机械法的主要应用设备，相对能耗小、效率高且产品粒度分布集中。但是由于粉体物料细化过程中随着粒径的减小易出现颗粒聚团现象，导致现有振动磨机制粉产品的颗粒粒径最小只能达到0.5 μm左右。因此，改善超细粉碎的团聚、不细化现状是必要的。

为解决超细粉碎硬团聚、不细化的技术难题，多年来国内外学者在振动粉碎领域进行了大量研究。BECKER等[3]通过实际试验证实物料粉碎效果的影响参数为振强和比能；GONZALEZ等[4]采用理论推导与试验相结合的方法证明了振强、振频与产品粒度间存在特定关系，在同等研磨时间下振强越大产品粒度越细；ROMANKOV等[5]通过实验确认振动磨粉磨效率随振强增加基本呈单调增趋势；GOCK等[6]提出具有不平衡振源的偏心振动磨配以大振幅，导致冲击力的集中，可有效提高振强，降低能耗；IMJ磨机研制者钱汝中基于共振理论说明在超细粉磨时应采用较高的振强[7]；徐波等[8]通过建立介质层的运动方程和仿真试验指出：在适当的振动强度下可以提高介质的能量传递率。上述研究均证实了颗粒细化的关键是提高振强并根据材料特性调整最佳振强，但其研究过程中只采用了恒定振频或简单变频的控制方法，碎磨过程振强成分单一，实际取得的效果有限[9-10]。

本文从振动磨破碎机理出发考察金刚石物料破碎与磨机电机转速间的关系，提出变频变矢径的双变激振控制方法并研究其优化组合范围，确定具有瞬态高振强特性的激励参数，并通过试验对该方法的有效性进行了验证。

1 振动磨机工作机理

振动磨机工作时筒内磨介可以看做离散的耦合系统[11-13]，借助高速摄影技术对振动磨机工作时筒内磨介的运动状态进行观察分析，可以将磨介的运动大致分为分层循环运动和抛射运动2种。

分层循环运动是指磨介群绕筒体瞬时中心做分层循环回转运动，考察其分层现象，如图1所示。

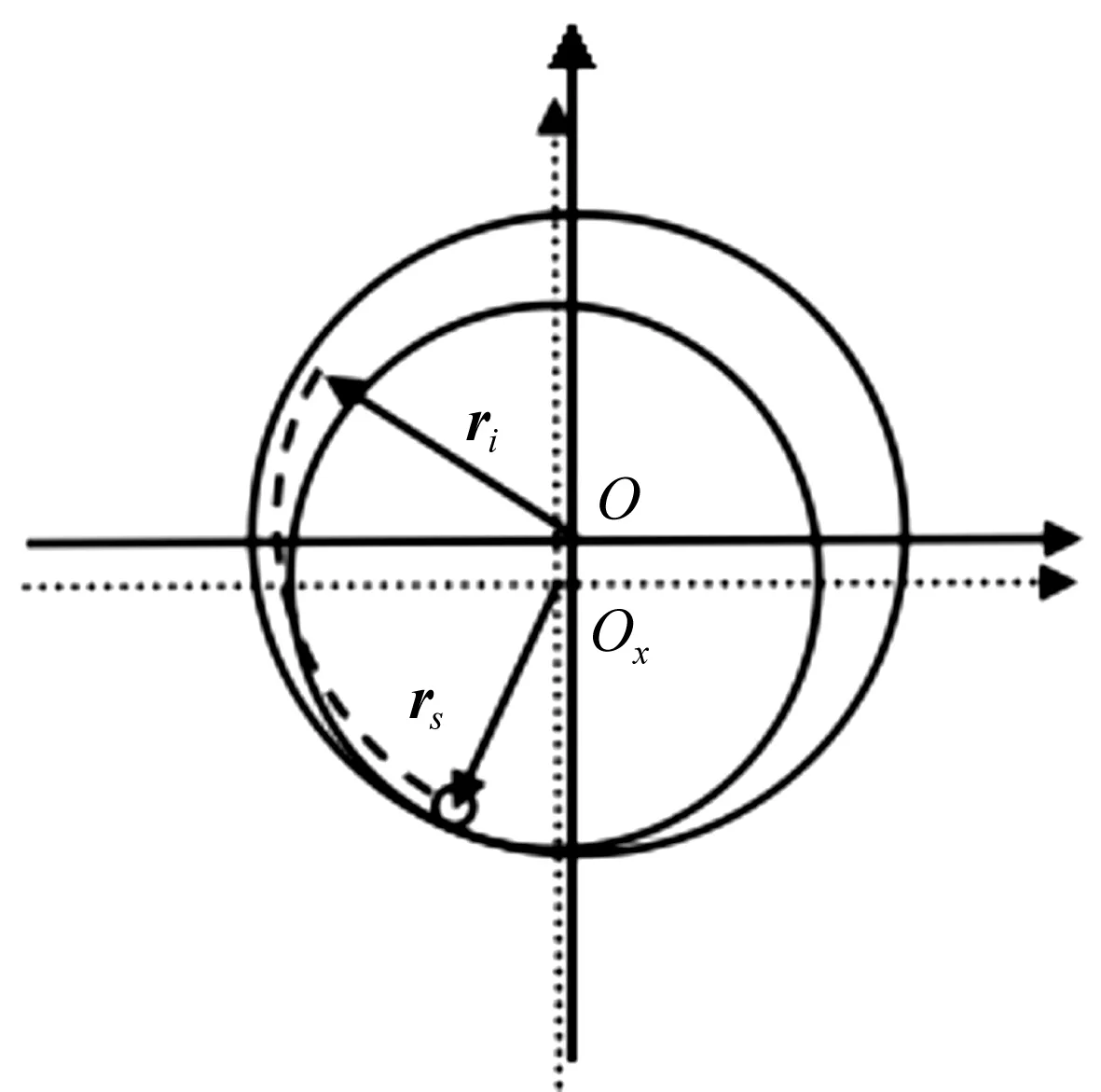
图1 磨介层分层运动位置矢量图Fig.1 Position vector diagram of grinding medium layer motion

对第i层磨介，其运动由磨介随磨介群的回转运动和随磨机筒体的运动合成，其位置矢量rp为：

rp=ri+rs

(1)

式中，ri为第i层介质相对筒体的位置矢量，rs为第i层介质相对瞬时回转中心的位置矢量。则第i层磨介层单个磨介的运动方程为：

(2)

式中，A为振动磨机振幅，ω为偏心块角速度，Rs为第i层介质对应的回转半径，ωs为第i层介质对应的回转频率，α,β为相位差，求导得速度方程：

(3)

则速度大小为：

抛射冲击运动是指磨介群做分层回转运动沿筒壁上升运动到最高点，磨介向上抛起，做抛射运动。抛射运动初速度的最大值和最小值，分别对应抛射轨迹线簇的上下边界，如图2所示。

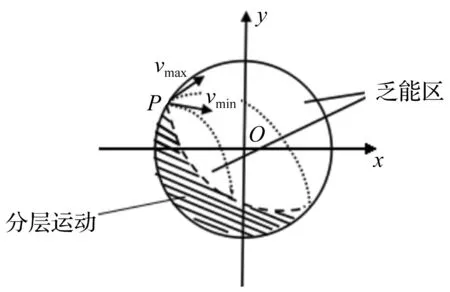
图2 磨介群冲击运动示意图Fig.2 Diagram of grinding medium impact motion

设磨介由P点抛射而出，P点坐标为(xp,yp),由牛顿第二定律可以得到其抛射运动轨迹为：

综上，分层循环运动和抛射冲击运动与磨机转速、磨筒振幅密切相关。转速越大，分层运动越明显；振幅越大，抛射运动越激烈。

平均粒径为10 μm的金刚石粉体，其晶体结构已趋于完美，且金刚石物料属于超硬材料，抗压强度远大于抗剪强度，应将回转运动对应的磨剥破碎作为主要破碎形式，增大筒体振动频率，辅以冲击破碎，形成超细金刚石粉体的最佳破碎形式组合。

为此，本文提出电机转速随时间变化的变转速激振方法。振动磨机工作时电机输出转速随时间变化从而引起一级、二级偏振块的当量矢径跃动产生瞬态高振强，以高振强的强势撞击力对物料解团聚，使颗粒进一步细化至1 μm以下。

2 双变激振振动磨模型建立

磨机工作时，偏心块产生的离心作用使得机体振动，偏心块在驱动电机的带动下产生离心力：

P0=m0rω2

其中，m0为偏心块质量，r为偏心块矢径，ω为电机输出转速。普通磨机的偏心块矢径为定值，得到的激振力为单一值，不利于增加筒内磨介与物料碰撞的几率。

将传统的偏心块变为二级偏心块组合，该组合偏块激振器具有变当量矢径功能，结构示意图见图3。电机输出转速随时间变化时，一级偏心块的速度会发生波动，利用该速度波动使具有独立运动的二级偏心块产生速度矢量的跃动变化，让夹角ψ2的变化具有时变性，则r1、r2合成当量矢径r也会随时间变化，从而形成变矢径激振方法。变转速变矢径激振方法可以使得激振力大小不断变化，形成振强成分多元化且具有瞬态高振强特性的激励方法。

1.一级偏心块 2.二级偏心块图3 二级偏心块结构示意图Fig.3 Structure of double eccentric block

双变激振振动磨是利用电机转速及偏心块矢径的时变性，使得磨机做高频、宽频振动。一方面，磨机的高频振动会让磨介与物料间产生冲击、摩擦、剪切等作用从而使物料破碎细化，另一方面，磨机的宽频振动会加剧磨介与物料间的相互作用，加快被磨物料的粉碎。

双变激振振动磨主要由筒体、支架、弹簧、激振电机、联轴器和偏心块组成，其虚拟样机仿真模型如图4所示，仿真基本参数如表1。偏心块尺寸及质量与实际物理样机保持一致。

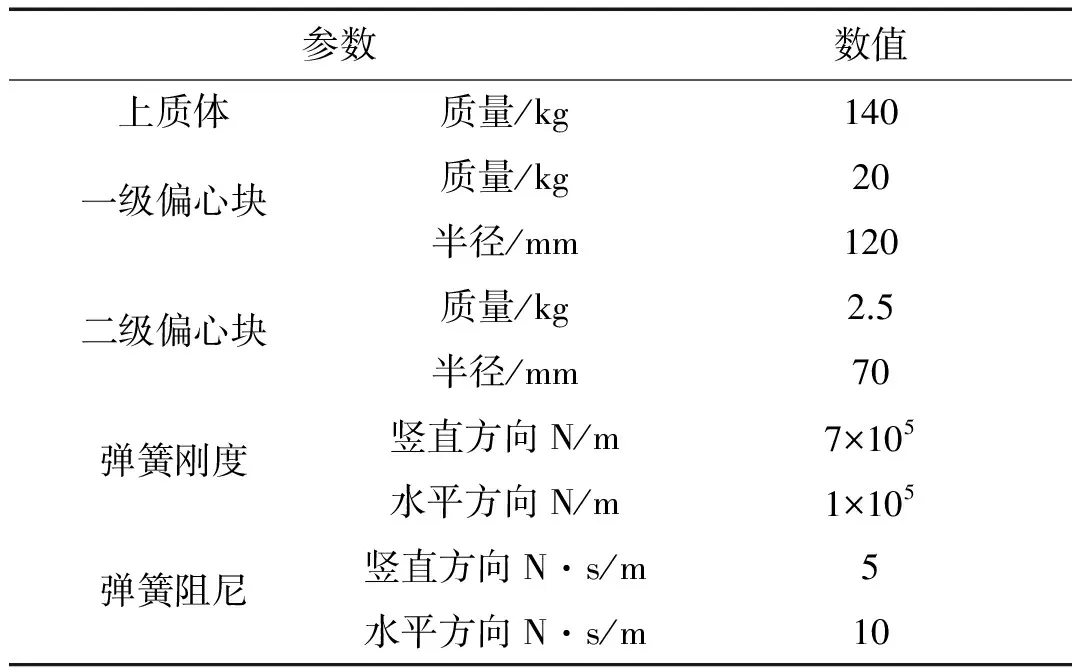
表1 仿真基本参数

1.上质体 2.变节距硬特性线弹簧 3.一级偏心块 4.二级偏心块 5.环形橡胶复合弹簧 6.筒体 7.振动电机 8.下质体图4 偏心振动磨示意图Fig.4 Schematic diagram of eccentric vibration mill

3 双变激振振动磨仿真试验

电机转速是影响振动磨机效率的一个重要因素，在固定球料比的条件下进行仿真分析，改变电机转速的同时保持其他参数不变，讨论振强K、振幅A及速度v在不同电机转速ω工况下的变化规律，探索电机转速ω的最佳变化范围。振强K定义如式(4)。

(4)

式中，A为振幅;ω为电机输出转速。

根据文献[14]，磨机振动强度通常取4～6，一般振强大于10时称为高振强。振强增大会降低磨机的抗疲劳寿命，且工程中为了减小机体惯性力，通常采用较小的振幅。设置振强最大值为30，振强变化范围为(5,30)，振幅在(5,10) mm内变化。

具体分析电机转速对振动磨机机体运动状态的影响，以1 000 r/min为电机基本转速，使转速以100 r/min为步长递增，转速变化范围由(900,1 100) r/min增大至(400,1 600) r/min，得到6种工况如表2，各工况下电机均采用正弦驱动。

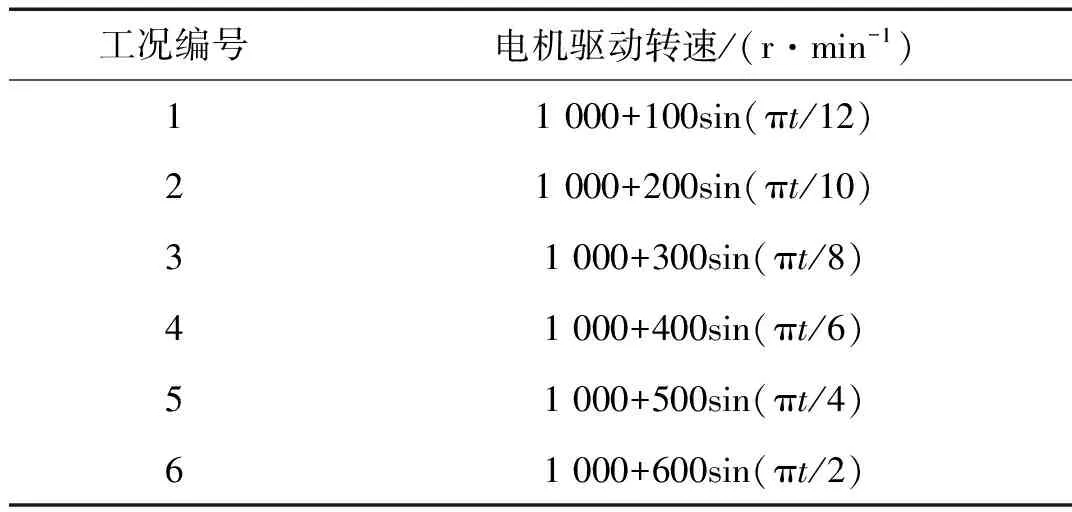
表2 振动磨机6种工况下电机驱动转速

磨机由电机直接驱动工作，机体的振动频率f机与电机的转速ω变化趋势一致，具体转换关系如式(3)。

(5)

式中,ω为电机驱动转速(r/min)。

由式(5)可知，电机驱动转速以正弦曲线变化时，机体振动信号的频谱图应为某一范围内连续变化的曲线，计算得各工况条件下振动磨机体振动的频率分布见表3。振动磨机物料粉碎过程中粒径随时间变化而需要不同的振频，由表3可知随着电机转速变化范围的增大，机体的振动频带越宽，有益于物料的研磨。

表3 各工况下机体振动频率分布

4 不同工况运动响应特性对比分析

对振动磨机6种工况下的运动响应特性及振强变化规律进行分析，可以进一步获得电机转速最佳变化范围及组合。

6种工况下机体振幅A在A≤5、A>5两区间的占比随工况的变化曲线见图5。由图5可知随着电机转速变化范围增大，筒体竖直方向的振幅在A≤5区间占比越小，在A>5区间占比越大。

图5 振幅A占比随工况变化曲线Fig.5 Proportion of amplitude versus conditon curve

提取振动磨机在不同转速工况下的振动速度v，并通过统计分析计算振动速度的平均值及标准差，得到如图6所示的变化曲线。

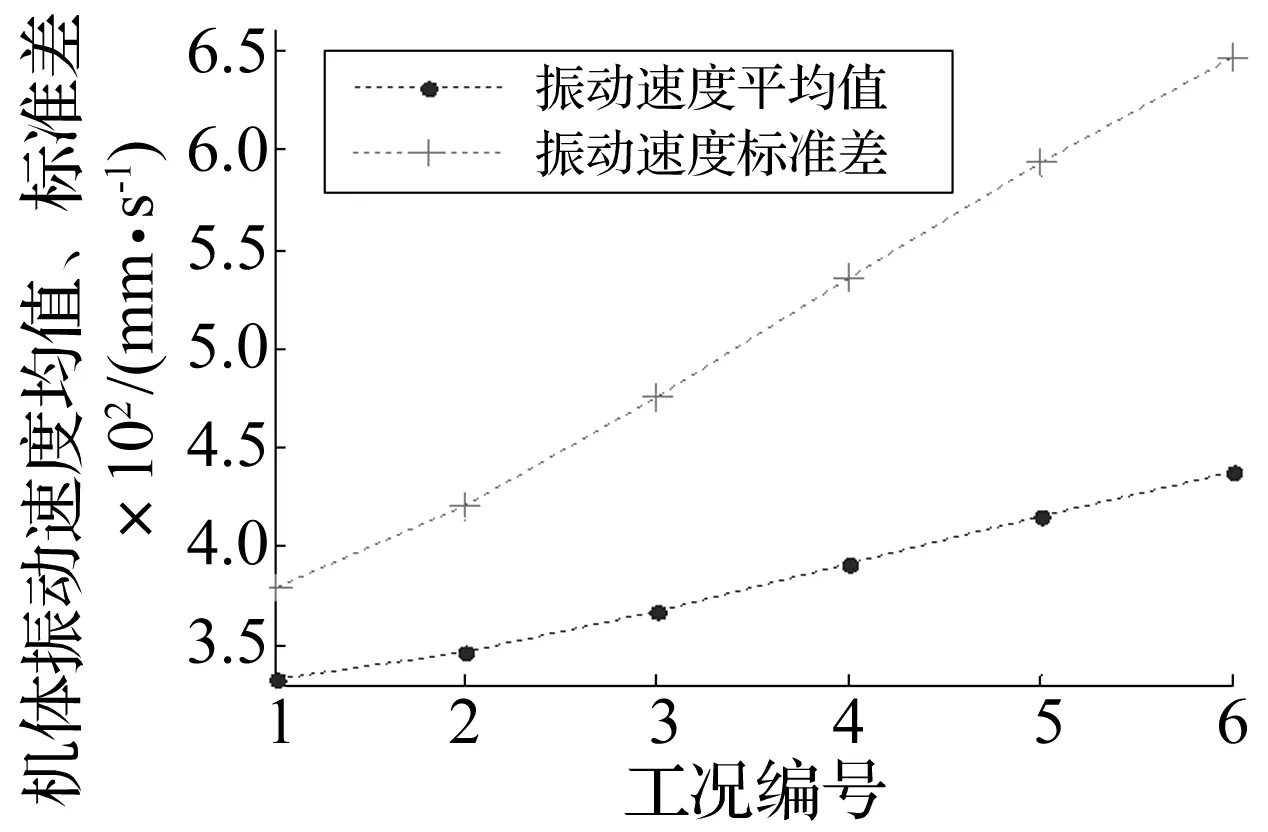
图6 不同工况振动速度平均值及标准差Fig.6 Average vibration velocity and standard deviation

由图6可知，机体振动速度的平均值及标准差均随着电机转速变化范围的增而增大，说明电机转速变化范围越大，机体的振动速度越大，振动越激烈，则筒壁传给磨介的初速度越大，研磨效果越强。

在分析了电机驱动转速对机体的振幅及速度的影响的基础上，讨论振强随电机驱动转速的变化规律。根据式(2)计算振强的最大值，并分析振强标准差的变化规律如图7所示。

图7 不同工况振强最大值及标准差Fig.7 Maximum vibration strength and standard deviation

如图7所示，机体振强最大值及标准差均随着电机转速的变化范围增大而增大。其中，第1工况下最大振强为8.31，高振强无占比，在选取电机转速时应避开该转速变化范围。

机体振强K在(0,10]、(10,20]、(20,30]这3个区间内的占比随工况变化，分别作出各区间振强K占比随工况的变化曲线如图8所示。

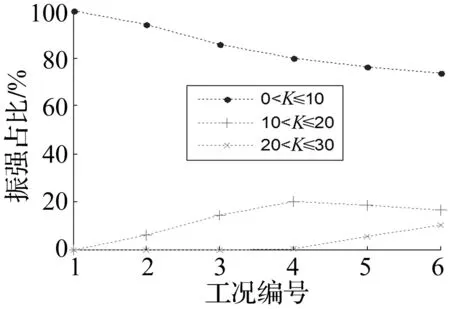
图8 不同工况振强K占比变化曲线Fig.8 Proportion of vibration strength versus conditon curve

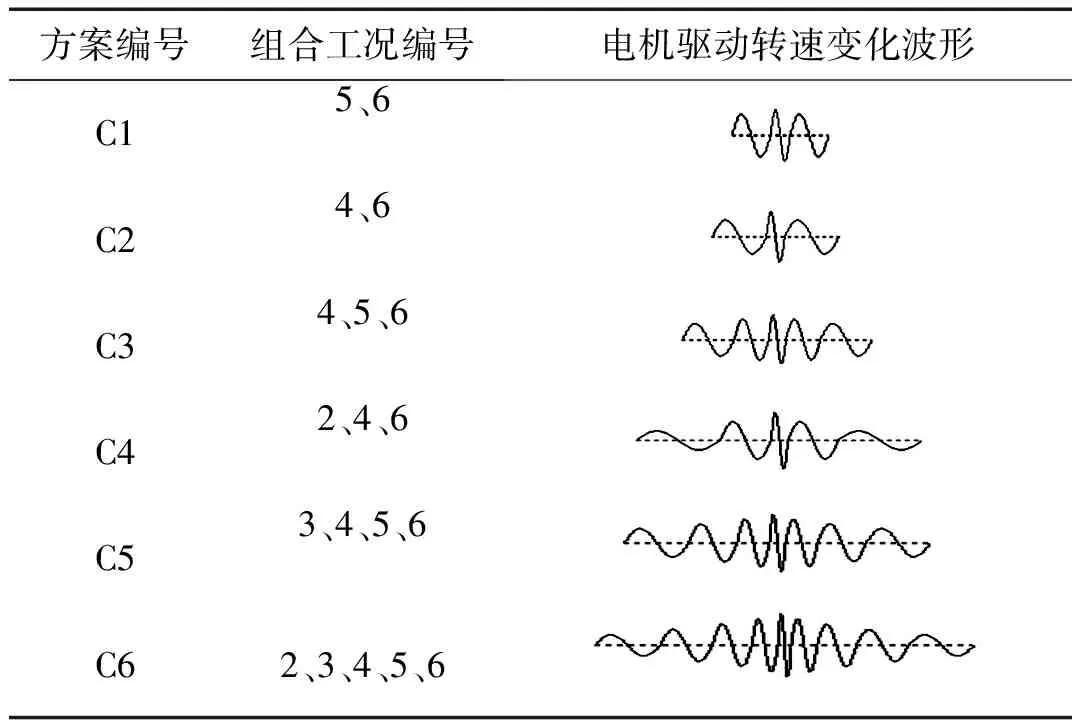
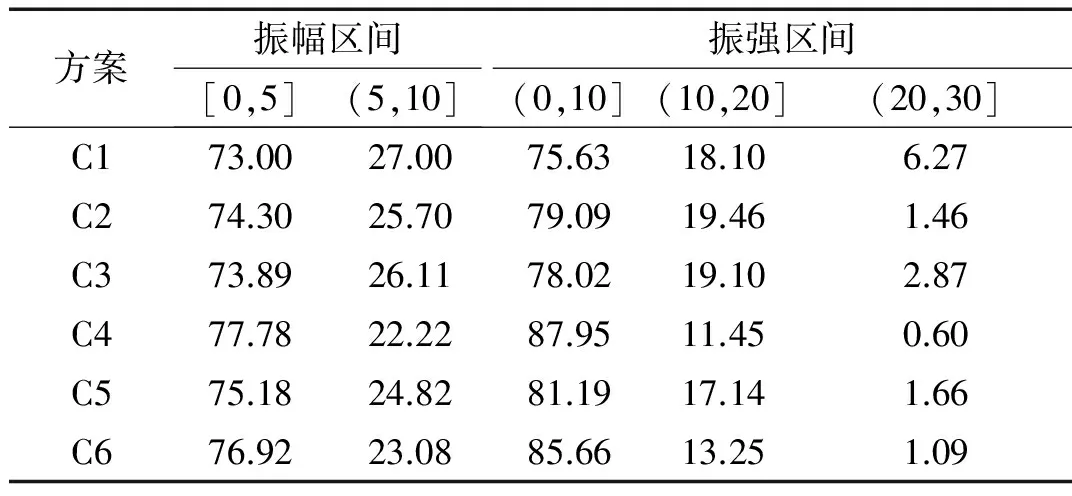
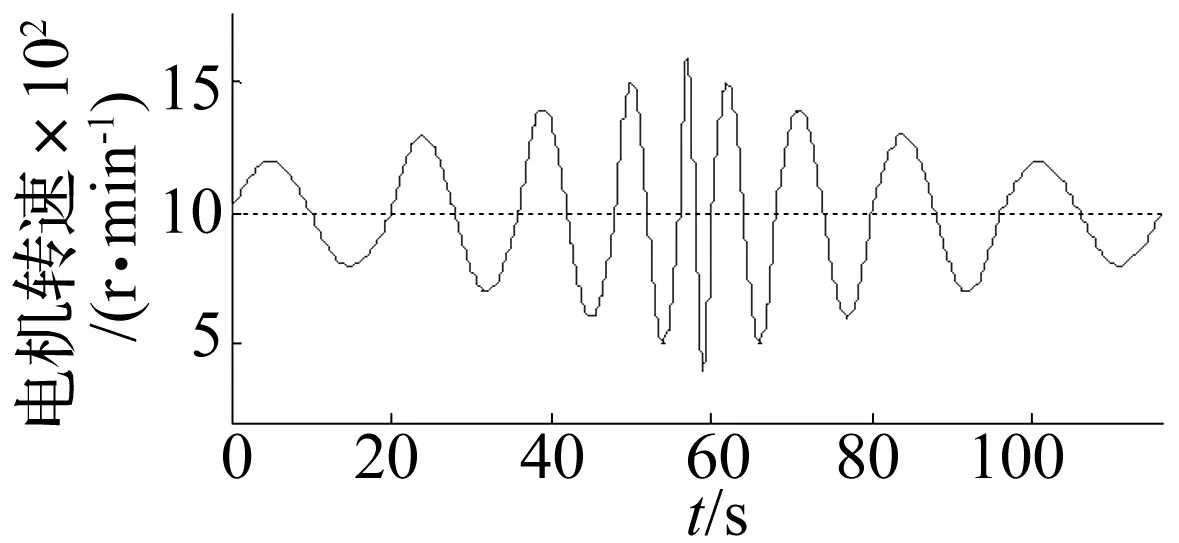
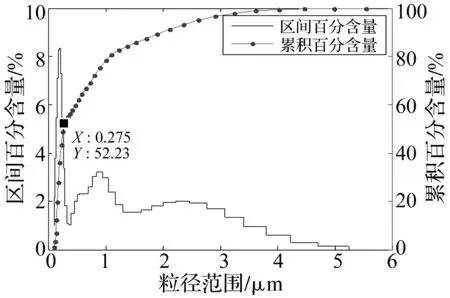
由图8可以看出，振强在(0,10]、(10,20]区间内的占比在第4工况后基本不随电机转速变化范围的增大而增大，但超高振强K(20

综上，振幅A>5区间占比随着电机转速的增大而增加；机体振动速度增长趋势明显，振动速度变化激烈；当电机最大转速大于1 400 r/min，即电机转速为第4、5、6工况时，磨机工作周期内出现一定比例的超高振强，振强的最大值和波动程度都随着转速的变化范围增大而增大。总体上，随着电机转速的增大，机体振动越剧烈，碎磨效果越好。

5 多工况组合优选

由上述不同工况运动响应特性对比分析可知，电机转速以单一工况对应的曲线变化时，振动磨机体振幅A、振强K分布并不理想，应采用多个工况的组合。除去工作周期内高振强及超高振强均无占比的第1工况，选择第2、3、4、5、6工况做组合优化，优先选取机体振动频带较宽的组合，同时为避免电机转速在变化过程中出现较大跳跃而损坏，工况组合采用对称分布组合，具体组合方案如表4。

表4 工况组合方案

分析各组合方案对应的振幅、振强分布规律如表5。为了保证振动磨机的正常运转，超高振强(20

表5 各组合方案对应的振幅、振强分布规律

方案C6对应的电机驱动转速变化曲线如图9，转速变化区间为400～1 600 r/min，变化周期为116 s。该变频驱动工况下，降低了高振幅占比，同时保证磨机工作周期内超高振强有占比，并将超高振强控制在振动磨机的正常工作强度内。

图9 优化后电机转速变化曲线Fig.9 Motor speed curve after optimization

6 物理样机粉磨试验

为了验证工况组合优化分析给出的电机转速优化曲线的有效性，分别对电机转速为恒定、电机转速按照优化曲线变化两种工况进行双变激振振动磨样机试验对比研究，以粉碎后的金刚石粉体颗粒的平均粒径以及颗粒断裂形貌作为评价指标，试验样机如图10，试验条件如表6。采用Labview测控系统[14]控制电机转速。

1.筒体 2.变节距硬特性线弹簧 3.振动电机图10 双变激振振动磨样机Fig.10 New vibration mill prototype

试验条件材料金刚石入料粒度10μm磨介填充率75%研磨时间120h

图11给出了优选前后后金刚石粉体产品的电镜扫描图像，由图像可以看出优化后金刚石粉体粒径有明显减小。利用Winners2000激光粒度仪测定试验后金刚石粉体产品的粒度大小及分布，测定结果如图12，更直观地比较了优选前后金刚石产品粒径的变化。

对比电机转速恒定和转速随优化曲线变化两种工况下的碎磨效果如表7。由表7知优化后金刚石粉体碎磨产品平均粒径为0.27 μm，而恒定转速工况下的金刚石粉体碎磨产品平均粒径为2.52 μm，优化后产品平均粒径有明显的减小。此外，由图11也可以看出优化后金刚石颗粒产品的粒度分布较窄。上述样机试验结果分析证实了电机转速优化曲线的有效性。

表7 不同工况下样机试验结果

图11 金刚石颗粒产品电镜扫描图像Fig.11 Diamond particle product SEM image

图12 优化后金刚石颗粒产品累积粒度分布图Fig.12 Product cumulative particle size distribution

7 结 论

通过本次研究得到如下结论：

(1)对于金刚石等超硬脆性颗粒，磨机应采用较大振频，将磨剥作为主要粉磨形式对物料进行细化的主要方式。

(2)电机转速是振动磨机粉磨过程中可控的主要影响因素，不仅会影响到筒内介质的运动状态外，还会对振强、振幅及振动速度等筒外运动参数造成影响。因此，确定了合理选择电机转速变化是提高粉磨效率的有效途径。

(3)双变激振振动磨工作时具有高振强以及适当的超高振强，有利于打破粉体聚团，使物料颗粒进一步细化，获得较好的粉磨效果。

[1] ZOU Jingchao, YANG Xiaolan, LIU Jifeng. Study on preparation of superhard nanopowder by chaos vibration with high strength [J]. Information Technology Journal, 2012, 11(4): 461-465.

[2] Microgrinding Systems Inc. The VKE mill energy comparative efficiency tests [R].Little Rock:Technical Report, 1991.

[3] BECKER M, KWADE A, SCHWEDES J. Stress intensity in stirred media mills and its effect on specific energy requirement[J]. International Journal of Mineral Procesiing, 2001, 61(3): 189-208.

[4] GONZALEZ G, D’ANGELO L, OCHOA J, et al. The influence of milling intensity on mechanical alloying [J]. Metastable, Mechanically Alloyed and Nanocrystalline Materials, 2002, 386(3): 159-164.

[5] ROMANKOV S, KALOSHKIN S D, HAYASAKA Y, et al. Effect of process parameters on the formation of Ti-Al coatings fabricated by mechanical milling[J]. Jounal of Alloys and Compounds, 2009, 484(1/2): 665-673.

[6] GOCK E, KURRER K E. Eccentric vibratory mills-theory and practice [J].Powder Technology, 1999, 105(1): 302-310.

[7] 罗帆，聂鸿丽，孔祥忠. 振动粉磨和振动破碎技术的发展回顾[J]. 中国水泥，2004(4): 41-45. LUO Fan, NIE Hongli, KONG Xiangzhong. Review on the development of vibration grinding and crushing technology [J]. China Cement,2004(4):41-45.

[8] 徐波，王树林，李生娟.振动磨碎机动力学分析及仿真试验[J]. 机械工程学报， 2008, 44(3):105-109. XU Bo, WANG Shulin, LI Shengjuan. Dynamic analysis and simulation of ground vibration test [J]. Journal of Mechanical Engineering,2008,44(3): 105-109.

[9] TANG Guoning, PENG Meng, LIU Wei, et al. Kinematic characteristics research of the superfine particles in the superfine vibration mill [J]. Applied Mechanics and Materials, 2011,103: 480-487.

[10] 刘极峰，杨小兰，邹景超. 新型高振强双质体振动磨的非线性振动[J].机械工程学报，2008, 44(7): 190-194. LIU Jifeng, YANG Xiaolan, ZOU Jingchao. The nonlinear vibration model with high vibrating intensity vibrating mill [J].Journal of Mechanical Engineering,2008, 44(7):190-194.

[11] 刘建芳，沈超. 立式振动磨磨介动力学分析及振动强度设计[J].机械设计与制造，2013(2): 51-58. LIU Jianfang, SHEN Chao. The design of vertical vibration analysis of dielectric dynamics and strength of vibration mill [J]. Mechanical Design and Manufacturing, 2013(2):51-58.

[12] 唐果宁，彭猛. 离散磨介群动力学特性数值分析[J].振动与冲击，2009, 28(8): 51-58. TANG Guoning, PENG Meng. Lumerical analysis on the dynamic characteristics of discrete grinding media [J].Journal of Vibration and Shock, 2009, 28(8): 51-58.

[13] 唐果宁，黄良沛，刘伟，等. 团聚性对超细振动磨机粉碎影响的试验分析[J].振动、测试与诊断，2013, 33(1): 48-51. TANG Guoning, HUANG Liangpei, LIU Wei, et al. Experimental analysis of the impact of agglomeration on the crushing of ultrafine vibration mill [J].Vibration, Testing and Diagnosis,2013, 33(1):48-51.

[14] 杨小兰, 刘极峰, 林莉, 等. 振动机械高振强性能的LabVIEW测控系统研究与试验[J]. 煤矿机械, 2014, 35(12):74-77. YANG Xiaolan, LIU Jifeng, LIN Li, et al. Research and test of measurement and control system for high vibration intensity of vibrational machine based on LabVIEW[J]. Coal Mine Machinery, 2014, 35(12):74-77.

Optimization of the motor speed of ultrafine vibration mill

GAO Yuan1, JIA Minping1, YANG Xiaolan2, LIU Jifeng2

(1.College of Mechanical Engineering, Southeast University, Nanjing 211189, China；2.College of Mechanical Engineering, Nanjing Institute of Technology, Nanjing 211167, China)

Material agglomeration is easy to appear during the ultrafine grinding process by ordinary vibration mill with constant motor speed. Because of that, the difficulty to refine the particles is increased and the development of ultra-fine powder is limited. A new excited mode with the motor speed changing over time was put forward, and an ultrafine grinding excitation method with high vibration strength was explored through Adams simulation and prototype experiments. The motion response characteristics of the body, the changing rule of vibration strength and the optimal range of motor speed were obtained through simulation analysis of vibration mill at different speed. Grinding tests on the new vibration mill were conducted with diamond powder as the grinding object, whose average particle size was 10 microns. The results show that the reasonable change of motor speed is conducive to the further refinement of particles.

vibration mill; ultrafine grinding; motor speed; high vibration strength

国家自然科学基金(51375221)

2015-07-30 修改稿收到日期：2016-01-11

高远 女，硕士，1992年生

贾民平 男，教授，博士生导师，1960年生

TH113.1

A

10.13465/j.cnki.jvs.2017.02.008