基于KVMD-PWVD与LNMF的内燃机振动谱图像识别诊断方法

牟伟杰， 石林锁， 蔡艳平， 孙 钢， 郑 勇

(第二炮兵工程大学 五系，西安 710025)

基于KVMD-PWVD与LNMF的内燃机振动谱图像识别诊断方法

牟伟杰， 石林锁， 蔡艳平， 孙 钢， 郑 勇

(第二炮兵工程大学 五系，西安 710025)

为了直接对内燃机振动谱图像进行诊断识别，提出一种基于改进变分模态分解(VMD)、伪魏格纳时频分析(PWVD)与局部非负矩阵分解(LNMF)的内燃机振动谱图像识别诊断方法。该方法首先针对VMD分解过程中的层数选取问题，提出了一种中心频率筛选的VMD分解层数改进方法(KVMD)，然后将内燃机振动信号利用KVMD分解成一组单分量模态信号，并对生成的各个单分量信号进行伪魏格纳分析处理后表征成振动谱图像；在此基础上，对生成的内燃机KVMD-PWVD振动谱图像分别采用非负矩阵分解(NMF)和LNMF形成编码矩阵，并采用最近邻分类器、朴素贝叶斯分类器和支持向量机对上述编码矩阵直接进行模式识别，以实现内燃机振动谱图像的自动诊断。最后，将该方法应用在内燃机故障诊断实例中，结果表明：该方法改进了传统图像模式识别中的特征参数方法，能有效诊断出内燃机气门间隙故障，三种分类器识别精度均大于93%，其中支持向量机的分类精度最高，达到99.8%，且采用LNMF形成的编码矩阵识别精度整体高于NMF，为内燃机振动诊断探索了一条新途径。

内燃机；故障诊断；时频分布；特征提取；局部非负矩阵

内燃机的振动信号是一种典型的非平稳的时变信号它包含了极其丰富的特征信息, 直接、快速、准确地反映内燃机的运行状态，因此一直是内燃机故障诊断研究的热点和前沿。

内燃机振动分析诊断法主要包括信号检测、信号处理、特征提取、模式识别四个环节，其中最关键也最困难的环节是故障信号的分析处理和特征提取，直接关系到故障诊断的准确性和故障早期预报的可靠性。针对内燃机振动信号的处理和特征提取，国内外学者开展了大量研究工作，如文献[1] 将图像分割理论引入柴油机故障诊断中，提出一种基于时频谱图、图像分割和模糊模式识别的柴油机故障诊断方法；文献[2] 提出一种基于自适应形态提升小波与改进非负矩阵分解的发动机故障诊断方法；文献[3]将对称极坐标方法和数字图像处理技术结合应用到柴油机故障诊断中；文献[4] 将高阶累积量与图像纹理特征提取方法相结合有效提取了柴油机振动信号的故障特征；这些方法为内燃机故障诊断提供了必要的方法，但是到目前为止，还没有形成一个“针对内燃机不同故障，采用何种时频分析方法，如何提取特征参数” 的共识。内燃机振动信号时频分析方法虽有许多，但往往选择越多时，如何去选择能更好刻画出内燃机不同故障振动信号非线性特征的方法就成为一个问题；在利用图像分析技术进行特征参数提取时，大多只是提取图像的单一特征量作为特征参数，特征指标选择模糊，易把一些重要的时频信息遗漏[5-8]，这些都对故障识别造成很大影响。针对以上存在的问题，提出了一种基于KVMD-PWVD振动谱图像生成，LNMF图像特征参数提取的内燃机故障诊断新方法。该方法实质是 “KVMD-PWVD振动谱图像生成→LNMF振动谱图像特征提取→分类器→设备故障状态识别”的故障诊断方法。

VMD(Variational Mode Decomposition)分析方法是由DRAGOMIRETSKIY等[9]提出的一种新的自适应信号处理方法。本文通过中心频率筛选，优化了变分模态分解K值的选取，并在此基础上提出了一种KVMD-PWVD时频分析方法。该方法不仅有效避免了WVD分布交叉项的干扰，而且保留了其优良特性，能够准确地表征出内燃机振动信号的特征。

在特征参数提取环节，针对传统NMF中存在非正交的基矩阵，导致数据冗余性较大，影响识别率的提高问题，提出采用局部非负矩阵(LNMF)[10]的方法。LNMF将图像描述为一个以基矩阵为码本, 系数矩阵为相应编码系数的矩阵乘积，文中取其编码系数矩阵作为特征参数。LNMF可以针对不同的图像自适应地计算图像的编码系数作为特征参数，数据降维效果明显，避免了不同图像特征指标的选择，而且具有明确的物理意义。

使用KVMD-PWVD和LNMF对内燃机气门间隙的四种工况信号进行了分析和特征参数提取，分别结合最近邻分类器(NNC)、朴素贝叶斯分类器(NBC)和支持向量机分类器(SVM)三种分类器进行诊断分类，平均识别正确率达到98.1%。实验结果表明KVMD-PWVD分析具有良好的时频特性，LNMF具有自适应特征参数提取和数据降维的优点，两者结合实现了对内燃机振动信号的自动化分析和诊断。

1 基于变分模态分解的魏格纳时频分布

1.1 变分模态分解

变分模态分解(Variational Mode Decomposition，VMD)是一种全新的自适应信号处理方法。VMD分解方法是通过迭代搜寻变分模型的最优解来确定每个本征模态分量(IMF)的频率中心及其带宽，实现了信号频域和各个分量的自适应剖分[11]，它是一种完全非递归的信号分解方法。

信号经过VMD被分解成一系列本征模态分量(IMF)，每个IMF都可以表示为一个调幅-调频uk(t)信号，表达式为

uk(t)=Ak(t)cos(φk(t))

(1)

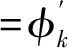
假设信号经VMD分解为K个IMF分量，则可得到变分约束模型：

(2)

式中：δ(t)为Dirac分布，*表示卷积。{uk}代表信号经VMD分解后得到的K个IMF分量，{uk}={u1,…,uk}；{ωk}为各个IMF分量的频率中心，{ωk}={ω1,…,ωk}。

为求取变分约束模型的最优解，引入二次罚函数项和拉格朗日乘子便可得到：

L({uk},{ωk},λ)=

(3)

式中：α为惩罚参数；λ为Lagrange乘子。

VMD方法中采用乘法算子交替的方法来求取上述变分约束模型，得到最优解将信号分解成为K个窄带IMF分量。

在进行变分模态分解时需要依靠经验预设分解层数K，这对VMD的自适应性造成了很大影响。信号VMD分解后得到K个本征模态分量(IMF)，每个本征模态分量都存在着一个频率中心ωk(t)。K值与ωk(t)有着密切的关系，K值选取的恰当与否，直接决定了分解结果的好坏。K值选取过小，对信号的分解不彻底，K值选取过大，会出现过分解现象。现在大多是采用观察中心频率的方法确定K，即先计算出多个不同K值下的中心频率，如果出现中心频率过于相近的情况，既认为出现了过分解。本文对VMD的分解层数K进行了优化，提出同一K值下，相邻中心频率的比值与阈值θ相比较来最终确定K值的筛选方法KVMD，经大量试验阈值θ取值为1.1。

KVMD算法的主要步骤为：

步骤1 初始化K值，(内燃机频带较宽，取K=3)。

步骤2 对信号进行VMD分解，得到K个IMF分量和每个IMF分量的频率中心ωk(t)。

步骤3 用前一个IMFk-1分量的中心频率ωk-1(t)比上后一个IMFk分量的中心频率ωk(t)得到一组频率比值λ1,λ2,…,λK-1(λk=wk-1/wk)。

步骤4 设定阈值θ=1.1。当λk>θ时，认为VMD分解不彻底，令K=K+1，重复步骤2～步骤3。

步骤5 当λk≤θ时可判定为IMFk-1和IMFk频率混叠，VMD出现了过分解，因此得出结果K=K-1，并输出其分解结果。

1.2 魏格纳时频分布

Wigner时频分布(WVD)是一种的非平稳信号分析的工具。作为一种能量型的时频联合分布，WVD时频分布与其它时频分布相比，具有真边缘性,弱支撑性,平移不变性等优良性质。由于双线性核函数的引入，使多个分量在时频平面发生耦合产生了交叉项。当信号中包括的分量成分越多，交叉项也越多，使WVD时频分布很难将有多个频率成分的信号表示清楚[12]。对WVD进行加窗处理，就得到了伪魏格纳分布(PWVD)。PWVD在时域上对交叉项有一定抑制作用。

WVD时频分布中出现频率混叠和交叉干扰现象的主要原因是被分析的对象不是单分量的信号。内燃机的振动信号频谱范围较宽成分复杂，若直接使用WVD对内燃机振动信号进行分析，得到的时频分布图往往很难将信号描述清楚。KVMD-PWVD时频分布是利用了线性时频表示满足叠加原理的思想。为消除交叉干扰项，可以将待分析的信号经KVMD分解成一组单份量信号，先对各个单分量信号单独进行伪魏格纳分析和处理，再将结果线性叠加组合成原信号的魏格纳时频分布。KVMD-PWVD时频分布结合了VMD在频域自适应剖分的特点和PWVD时域抑制交叉干扰项的优点，既有效地消除了WVD的交叉干扰项，又保留了WVD时频分布的优良特性。

信号x(t)的KVMD-PWVD时频分布定义为：

KVMD_PWVDx(t,f)=

(4)

KVMD-PWVD时频分布算法的主要步骤为：

步骤1 首先对待分析信号进行KVMD分解，生成一组本征模态分量IMF1,IMF2,…,IMFK。

步骤2 对各个本征模态分量IMF首先进行希尔伯特变换然后进行PWVD分析(本文窗函数类型及大小均采用默认值)。

步骤3 将分析结果进行线性叠加得到KVMD-PWVD时频分布结果。

2 局部非负矩阵分解

局部非负矩阵(LNMF)分解方法在非负矩阵分解(NMF)[13]基础上提出的，其根本目的是为了使分解后的基图像能够得到更为局部的特征，该方法已经被成功用于人脸识别中[14-15]。LNMF算法是通过对K-L散度目标函数施加基的列正交性约束，以减少基向量之间的冗余。

LNMF的目标函数如下式所示：

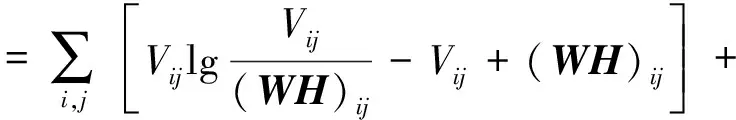
(5)

其迭代公式如下所示：

(6)

(7)

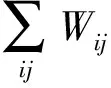
(8)

使用局部非负矩阵直接对时频分布图像进行特征参数的提取，数据的降维效果明显，简化了计算，避免了复杂的图像运算和传统方法复杂参数的设置问题，具有很好的自适应性。

3 燃机故障诊断实例

3.1 内燃机实验工况

本文所用的内燃机台架由BF4L1011F型柴油机、传动轴、电机和控制台四部分组成。取内燃机缸盖表面振动信号对内燃机进行故障诊断，采样频率25 kHz，转速为3 000 r/min，测试过程中，内燃机空载运行，实验平台如图1所示。在正常状态下，BF4L1011F柴油机的进气门间隙应调整为0.25～0.30 mm，排气门间隙应调整为0.35～0.40 mm。实验中模拟了常见的4种气门间隙状况，分别对应气门间隙正常与不当，具体情况如表1。其中，正常进、排气门间隙0.3 mm、0.4 mm，气门间隙过小为0.06 mm，气门间隙过大为0.6 mm，严重漏气为开口4 mm(长)×1 mm(宽)。实验共采集内燃机气门4种故障状态下各70种振动信号样本，总计280个。

图1 试验平台Fig.1 Experimental platform

Tab.1 Four states of IC engine’s valve train mm

状态编号1234进气门0．300．300．300．30排气门0．400．060．60开口4×1

3.2 内燃机智能故障诊断流程

基于KVMD-PWVD与LNMF的故障诊断方法对内燃机的故障诊断，共分为以下几个步骤：首先对采集到的内燃机振动信号进行KVMD-PWVD时频分析得到时频分布图像，然后采用局部非负矩阵对时频图像进行分解得到图像的特征参数，最后用分类器对特征参数进行分类完成对内燃机的故障诊断，方法步骤如图2所示。

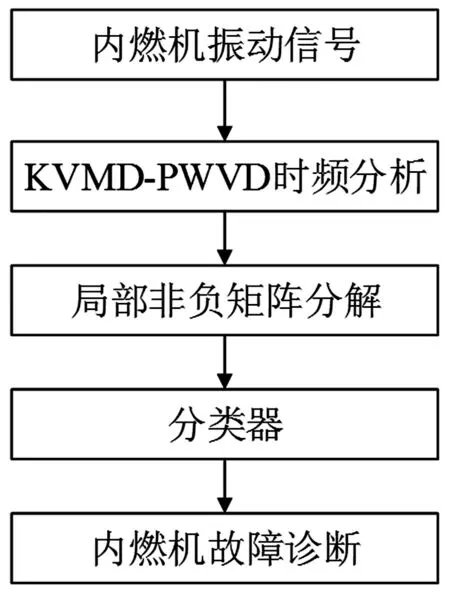
图2 基于KVMD-PWVD与LNMF的故障诊断方法的步骤Fig.2 Fault diagnosis method based KVMD-PWVD and LNMF

3.3 内燃机缸盖振动信号的KVMD-PWVD时频分析

首先取内燃机气门间隙正常工况下的缸盖振动信号，并绘制其时域分布图，功率谱图，WVD时频分布图和KVMD-PWVD时频分布图，为使时频图与信号的时域和频率一一对应，将信号时域图和功率谱图分别放在时频分布图的上方和左侧，如图3和图4所示。

图3 振动信号的WVD时频图Fig.3 WVD image of vibration signal

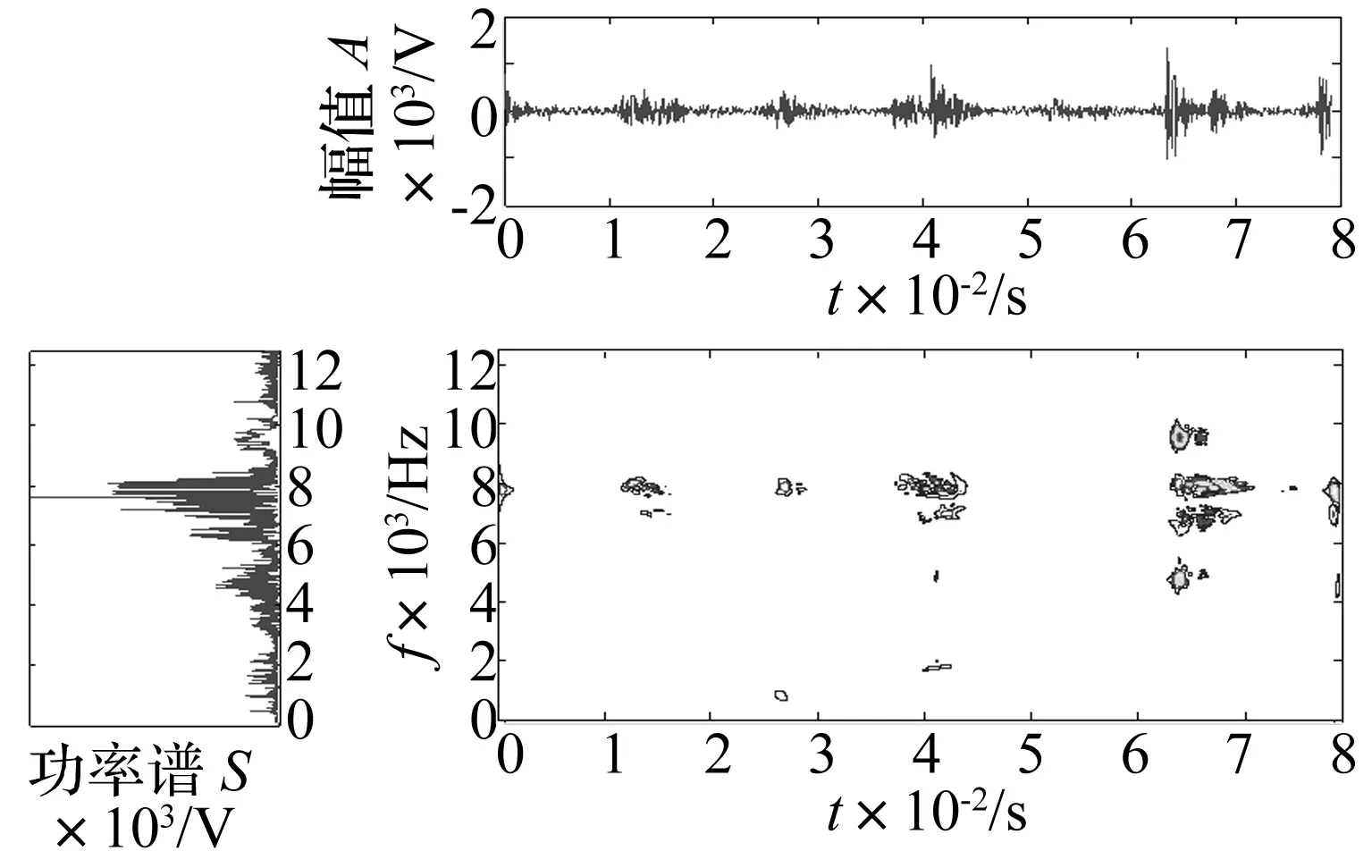
图4 振动信号的KVMD-PWVD时频图Fig.4 KVMD-PWVD image of vibration signal

从图3的时域波形图可以看出，在0 ms附近、25～29 ms之间、37～44 ms之间、62～66 ms之间、以及77 ms处，振动信号有较大的振动幅度，振动幅度最大处发生时刻大约在62～66 ms时间段内，从功率谱图中可看出振动信号的频谱主要集中在6～10 kHz。但是时域波形图和功率谱图不能直观的反应出时间、频率和幅值三者的关系。

为使图像更加清晰, 便于观察, 文中给出的时频分布图像是用等高线表示的,横坐标与时域波形图一一对应表示时间，纵坐标与功率谱图一一对应表示频率，颜色代表幅值。然而在实际的故障诊断中,为便于计算与特征提取，使用的都是灰度图像，灰度越深振动幅值越大。对比图3和图4可得，图3用WVD方法对缸盖振动信号进行时频分析时存在严重的交叉干扰项，这给分析造成了很大影响。而图4中KVMD-PWVD方法可以有效地抑制WVD方法的交叉项。该方法清晰地分辨出在0 ms附近存在有8 kHz的频率；25～29 ms时间段附近，振动信号存在6.5～8 kHz 的频率；37～44 ms时间段内存在2kHz和 6～10 kHz频率；62～66 ms时间段内存在在5～ 9 kHz频率；77ms时振动信号的频率为6. 5～ 8. 5 kHz。这些重要的时频信息是振动信号傅里叶频谱和WVD所不能反映的。

采用KVMD-PWVD时频分析方法分别对其余三种故障工况的柴油机缸盖振动信号进行处理得到其时频分布图，如图5所示。

图5 三种典型工况缸盖振动信号的KVMD-PWVD时频分析Fig.5 KVMD-PWVD time-frequency image for three states

气门机构其主要故障有两种：一是气门机构的间隙异常，二是气门机构的气门漏气。若气门间隙过小，气门受热膨胀后，会使气门密封不严，导致气门烧蚀，燃烧不良，功率下降，油耗增加；而气门间隙过大，则使进、排气门迟开、早关，使进、排气的时间变短，造成进气不足，排气不净，使工质更新恶化，还会使气门与气门推杆间撞击严重，磨损加剧，造成噪音过大等故障现象；而气门漏气则会直接引起内燃机的功率下降，气门烧蚀等故障，使内燃机工作不稳定。由于内燃机气缸盖直接承受气缸压力和气门机构冲击等作用力，这些激励力是各自按一定的规律作用于缸盖系统，并且频率特性也各不相同，因而作为对这些激励力的响应，缸盖表面振动信号是由一系列频率、幅值差别较大的瞬态响应组成。通过对缸盖振动信号进行时频分析，在生成的时频图像中不同工况的时间、频率和幅值的差别较大，可以通过不同工况图像之间的差异来进行故障分类。

比较图4和图5可以看出，缸盖振动信号的频率主要出现在5～12 kHz之间的高频区，各个故障时频分布图呈现出较大差异。故障信息在时频图上出现和消失时间不同，幅值大小不同，并且它们频率组成更不相同。当气门间隙过小时，频率主要集中在9～12 kHz；气门间隙过大时，频率主要集中在11～12 kHz；气门漏气时，频率主要集中在10～11 kHz。KVMD-PWVD时频分布图能清楚显示出内燃机缸盖振动信号每一时刻的频率分布情况，提取其中的峰值及对应的时间和频率作为特征量就可以对四种工况进行分类。

3.4 KVMD-PWVD时频谱的局部非负矩阵分解

取采集到的280个信号作为研究对象并分别作其KVMD-PWVD时频分布图，相应得到293×401个像素点的时频矩阵。由于得到时频矩阵维数高，计算量大，不利于进行特征参数的提取，因此在保留时频图像主要特征的前提下，对图像进行预处理，将其转化为90×120的灰度图像。

KVMD-PWVD时频谱的局部非负矩阵特征参数提取流程如下:

步骤1 对预处理所得到的时频矩阵进行重排操作，将每个时频矩阵由90×120维变形为10 800×1维列向量，并对其进行归一化处理;

步骤2 从四类工况时频分布图中每一类随机选取30幅共120幅，组成LNMF样本集V，V的维数为10 800×120;

步骤3 对样本集V进行LNMF分解，可得特征矩阵W，W的维数为10 800×r。r表示特征维数，它的取值对LNMF分解的结果和后续的识别精度有较大影响;

步骤4 将所有时频图像向基矩阵W投影，可得280个系数向量H，H的维数为r×1。每一个系数向量H代表了它所对应的时频图像;图6给出的是特征维数r=60时，KVMD-PWVD时频分布图像训练集对应的特征系数。为方便表示，将每一个样本的特征系数矩阵对应成图中的一行编码矩阵，维数为1×60，图中每个像素的灰度值严格与样本系数值一一对应。图6(a)、(b)、(c)、(d)各代表一种内燃机工况，依次为气门间隙正常、气门间隙过小、气门间隙过大和气门漏气。可以看出LNMF对数据进行了非常有效的降维，将10 800维数据压缩到60维，大大降低了识别复杂度和计算量。从图中可以看出，同种工况编码矩阵各像素灰度值较为相似，不同工况间编码矩阵各像素灰度值区别较大，而灰度值又与工况系数一一对应，说明同种工况的系数很相近，不同工况的系数差异大，说明所提取的特征参数有利于后续的分类计算。

图6 LNMF提取的测试集特征系数 Fig.6 Test set features parameters for LNMF

3.5 故障分类

支持向量机是基于统计学习理论的一种新的学习机器。SVM与传统学习机器相比具有适合小样本学习、推广能力好、对数据维数不敏感等优点[16]，因此本文选择SVM作为对内燃机运行工况判别的智能学习机器。

在对内燃机气门间隙工况进行分类时，从四类工况中每一类中随机选出30个系数向量H共120个，组成训练样本集合用于训练SVM。采用5重交叉检验法选择最优的RBF核函数参数σ和惩罚系数C，σ=2.5，C=250。然后用剩余的160个系数向量对训练好的SVM进行分类测试，用识别正确率作为指标来评价文中方法的性能。

在利用LNMF对时频分布图进行分解过程中涉及特征维数对识别准确率的影响。为研究特征维数r对识别准确率的影响，本文采用不同的特征维数r对KVMD-PWVD时频分布图进行LNMF分解。结果如图8所示。从图8中可以看出，取得当基向量的特征维数较小时，识别率准确率不高；随着特征维数的不断增加，识别率准确率不断提高，当特征维数r=40～70时，所提取的特征参数取得了最优的识别准确率；然而随着特征维数的继续增加，识别准确率反而有下降的趋势。这是因为特征维数的大小反映的是原时频分布图的特征图像多少，每个数据集的特征空间的维数都是确定的，当特征维数r的取值等于特征空间的维数时，得到的基图像刚好可以重构所有原始图像，此特征空间的基最有意义；当特征维数r的取值小于特征空间的维数时，虽然数据降维效果明显，但是损失了图像特征信息，得到的基不足以描述整个空间，导致识别准确率率的降低；当特征维数r的取值大于特征空间的维数，得到的基才有可能描述整个特征空间，但过大的特征维数大时，不仅降维效果不好，还有可能带入信息冗余和噪声，影响识别率。图7中，当r=1时，得到的基向量远不能描述整个空间，所以识别率最低；随着特征维数r的增大，识别准确率不断提高，当特征维数r处于40～70的区间内时识别准确率取得最大值；随着r继续增大，在r>70的区间内识别准确率又有所减小。文中实验选取特征维数r=60。

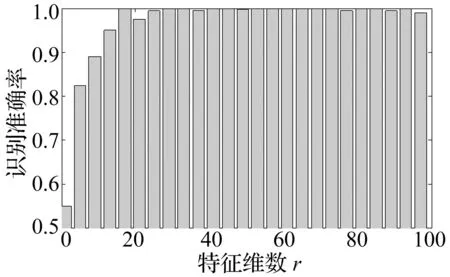
图7 工况特征识别率Fig.7 Recognition rate of LNMF feature extraction method

为验证KVMD-PWVD和LNMF方法所提取特征参数的通用性，使用KVMD-PWVD和NMF与文中方法进行比较，并选用多个分类器进行故障诊断分类。首先使用NMF方法和LNMF分别对KVMD-PWVD时频分布图进行特征参数提取，然后选用最近邻分类器(KNNC)、朴素贝叶斯分类器(NBC)和支持向量机分类器(SVM)三种分类器进行诊断分类，重复以上实验30次取平均值。实验结果如表2所示。

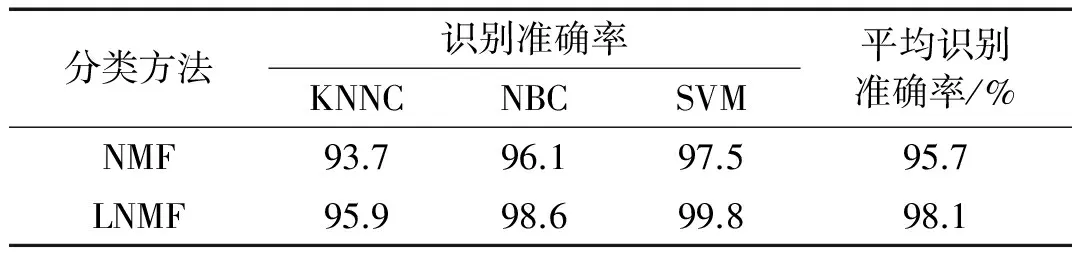
表2 内燃机故障诊断精度

由表2可以看出对KVMD-PWVD和LNMF方法所提取的特征参数采用不同的分类器，平均识别准确率达到98.1%明显高于采用NMF特惨参数提取法的95.7%；且采用多个分类方法，识别准确率都在95.9%以上；说明该方法识别准确率高，具有较好的通用性，适用于内燃机气门间隙的故障诊断。

4 结 论

(1)对VMD分解中K值的选取进行了优化增强了VMD分解的自适应性，并在此基础上提出了KVMD-PWVD时频分析法，该方法能够有效抑制WVD中存在的交叉干扰项，不仅可对内燃机振动信号的全部信息进行描述，还能提供任一局部时间信号变化的激烈程度信息。用该方法对不同气门间隙工况进行分析，各工况的时频分布特征明显。

(2)用LNMF分解对KVMD-PWVD时频谱提取特征参数，进行故障分类，并对LNMF分解中的特征参数对识别准确率的影响进行了研究。结果表明，LNMF既能对数据进行有效降维，又能不丢失图像有效信息，对时频分布图特征参数的提取自适应性好，且相比于NMF方法，LNMF的故障识别准确率高。

(3)将提取的特征参数分别用最近邻分类器(KNNC)、朴素贝叶斯分类器(NBC)和支持向量机分类器(SVM)三种分类器测试其识别准确率，得出基于KVMD-PWVD振动谱图像生成，LNMF图像特征参数提取的方法，可适用于内燃机气门间隙的故障诊断，且具有很高的识别准确率。

[1] 蔡艳平,李艾华,王涛,等.基于时频谱图与图像分割的柴油机故障诊断[J] .内燃机学报,2011,29(2):181-186. CAI Yanping,LI Aihua,WANG Tao,et al.IC diesel engine fault diagnosis based on time-frequency spectrum image and image segmentation [J]. Transactions of CSICE, 2011，29(2)：181-186．

[2] 李兵，徐榕，贾春宁，等.基于自适应形态提升小波与改进非负矩阵分解的发动机故障诊断方法[J].兵工学报，2013，34(3)：353-360. LI Bing, XU Rong, JIA Chunning, et al.Engine fault diagnosis Utilizing adaptive morphological lifting wavelet and improved non-negative matrix factorization[J].Acta Armamentarii, 2013，34(3)：353-360.

[3] 任金城，张玲玲，肖云魁，等.基于对称极坐标和图像处理的柴油机故障诊断研究[J].车用发动机，2013， 6(209)：80-85. REN Jincheng, ZHANG Lingling, XIAO Yunkui, et al. Diesel engine fault diagnosis based on symmetrical polar coordinate and image processing [J].Vehicle Engine, 2013，6(209)：80-85.

[4] 沈虹，赵红东，梅检民，等.基于高阶累积量图像特征的柴油机故障诊断研究[J].振动与冲击，2015，34(11)：133-138. SHEN Hong, ZHAO Hongdong, MEI Jianmin, et al. Diesel engine fault diagnosis based on high-ordercumulant image features[J]. Journal of Vibration and Shock, 2015，34(11)：133-138.

[5] 毛永芳,秦树.重分配谱图和多窗谱在机械故障诊断中的应用[J].振动与冲击,2009,28(1):161-165. MAO Yongfang,Qin Shu. Re-allocation of spectrum and multi-spectral windows and its application in machinery fault diagnosis [J].Journal of Vibration and Shock,2009,28(1):161-165.

[6] 王成栋，张优云，夏勇. 基S变换的柴油机气阀机构故障诊断研究[J].内燃机学报，2003，21(4):271-275. WANG Chengdong,ZHANG Youyun,XIA Yong.Fault diagnosis for diesel valve train based on S Transform[J]. Transaction of CSICE, 2003，21(4):271-275.

[7] 王成栋，张优云，夏勇. 模糊函数图像在柴油机气阀故障诊断中的应用研究[J]. 内燃机学报，2004，22(4)：162-168. WANG Chengdong,ZHANG Youyun,XIA Yong.Study on the use of ambiguity function images in fault diagnosis for diesel valve train[J]. Transaction of CSICE, 2004，22(4)：162-168.

[8] HUANG N E, SHEN Z,LONG S R, et al. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London, Series A,1998,454:903-995.

[9] DRAGOMIRETSKIY K,ZOSSO F. Variational mode decomposition [J]. IEEE Transactions on Signal Processing, 2014,62(3):531-544.

[10] LI S Z, HOU X W, ZHANG H J, et al. Learning spatially localized,parts-based representation[J]. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2001,1:207-212.

[11] 唐贵基，王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J].西安交通大学学报，2015，49(5)：73-80. TANG Guiji, WANG Xiaolong. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J].Journal of Xi’an Jiaotong University, 2015，49(5)：73-80.

[12] 蔡艳平，李艾华，王涛，等．基于EMD-Wigner-Ville的内燃机振动时频分析[J]．振动工程学报，2010，23(4)：430-437． CAI Yanping,LI Aihua,WANG Tao,et al. IC engine vibration time-frequency analysis based on EMD-Wigner-Ville[J].Journal of Vibration Engineering, 2010，23(4)：430-437．

[13] LEE D D, SEUNG H S. Learning the parts of objects by no n-negative matrix factorization [J].Nature,1999,401(6755):788-791.

[14] 刘昱昊.基于非负矩阵分解算法的人脸识别技术的研究[D]. 吉林：吉林大学，2014．

[15] 袁宝华, 王欢，任明武. LBP与LNMF特征融合的人脸识别[J].计算机工程与应用, 2013, 49(5):166-169. YUAN Baohua,WANG Huan,Ren Mingwu.Fusing local binary pattern and LNMF of face recognition[J].Computer Engineering and Application, 2013, 49(5):166-169.

[16] 向阳辉，张干清，庞佑霞.结合SVM和改进证据理论的多信息融合故障诊断[J].振动与冲击，2015，34(13)：71-77. XIANG Yanghui, ZHANG Ganqing, PANG Youxia. Multi-information fusion fault diagnosis using SVM & improved evidence theory[J]. Journal of Vibration and Shock, 2015，34(13)：71-77.

IC engine fault diagnosis method based on KVMD-PWVD and LNMF

MU Weijie, SHI Linsuo, CAI Yanping, SUN Gang, ZHENG Yong

(Department NO.5, the Second Artillery Engineering University, Xi’an 710025, China)

In order to directly diagnose and recognize IC engine vibration spectrum images, based on the improved variational mode decomposition (VMD) , pseudo Wigner-Ville time-frequency analysis (PWVD) and local non-negative matrix factorization (LNMF), an IC engine vibration spectrum image recognition and diagnosis method was proposed. Aiming at the VMD layers selection during the decomposition process, a center frequency selected VMD decomposition method (KVMD) was proposed, then the vibration signal of IC engine was decomposed into a set of single component modal signals by KVMD, and each single component of the signal, by using PWVD, was characterized as a vibration spectral image. On this basis, to get a code matrix, the non-negative matrix factorization (NMF) and local non-negative matrix factorization (LNMF) were used to the IC engine KVMD-PWVD vibration spectral image, and the KNNC, NBC and SVM were applied to the code matrix for pattern recognition in order to realize the automatic diagnosis of vibration spectrum images. The method has been used in practical IC engine fault diagnosis and the results show that the method improves the traditional characteristic parameters of image pattern recognition, it can effectively diagnose the IC engine valve clearance fault, the recognition accuracy of the three classifiers is all not less than 93%, the SVM has the highest classification accuracy which reaches 99.8%, and the code matrix using the LNMF has higher accuracy than the NMF. The method explores a new way for the IC engine vibration diagnosis.

internal combustion (IC) engine；fault diagnosis；time-frequency distribution；feature extraction；local non-negative matrix factorization(LNMF)

国家自然科学基金青年基金项目(51405498)；陕西自然科学基金项目(2013JQ8023)； 中国博士后基金资助项目(2015M582642)

2016-03-10 修改稿收到日期：2016-05-03

牟伟杰 男，博士生，1984年生

石林锁 男，教授,博士生导师，1958年生

TK428

A

10.13465/j.cnki.jvs.2017.02.007