龙门加工中心移动横梁静动态分析及结构改进*

鞠家全，任 东，崔德友，刘传进，邱自学

(1.南通大学 机械工程学院，江苏 南通 226019；2.南通国盛机电集团有限公司，江苏 南通 226003)

龙门加工中心移动横梁静动态分析及结构改进*

鞠家全1，任 东2，崔德友2，刘传进2，邱自学1

(1.南通大学 机械工程学院，江苏 南通 226019；2.南通国盛机电集团有限公司，江苏 南通 226003)

机床移动横梁因自身重力及外加载荷而发生变形，为此，对横梁进行了简化，得到其振动力学模型，理论计算求解出横梁最大变形量和一阶固有频率。对移动横梁进行了三维建模与有限元分析，横梁最薄弱位置位于横梁上下导轨部位，针对最薄弱部位，对横梁上下导轨局部结构进行了改进设计。结果表明，横梁结构理论计算的最大变形量和一阶固有频率与仿真结果相近，优化后的横梁形变减小了10.6%，质量减轻了136kg，轻量化效果明显。为机床其他零部件的优化设计提供了有益的方法参考。

龙门加工中心；横梁；优化设计 ；轻量化；有限元分析

0 引言

机床作为制造机器的机器，在航空航天、船舶机械，汽车等行业中得到广泛的应用。作为机床的主要结构部件，机床横梁在机床的动、静态性能方面起到极为重要的作用[1]。对于移动横梁，因自身重力及外载荷作用引起的横梁形变对机床加工性能有着重要的影响，因此减轻移动横梁的重量，提高横梁刚性对横梁系统结构的优化设计意义重大。

国内外在机床关键零部件的研究上主要采用优化筋板整体结构，利用仿生学原理布置筋板结构，优化零部件外形尺寸等方法，从而达到优化设计的目的。文献[1]对筋肋分布形式进行拓扑优化设计，从而提高横梁静、动态特性。文献[2]采用仿真分析软件，证明了横梁中部导轨—滑块结合部是横梁最薄弱地方，同时分析了导轨接触刚度和导轨接触阻尼对系统固有频率的影响情况；文献[3] 分析了横梁四种筋板结构，论证了O字型设计的最优性及O字高与宽的比值越接近1，横梁性能越好。文献[4]采用了仿生学原理，对机床立柱进行优化设计，提高立柱性能。SOROKIN S V等人对梁单元进行了能量流动的分析与优化[5]。

然而上述方法考虑了如何合理选择和布置筋板结构及筋板的厚度，对横梁有限元仿真分析主要集中在横梁最薄弱的中间位置，忽视了其它位置横梁的形变情况，也未直接提出针对薄弱位置的结构改进措施。本文中构建了横梁振动力学简图，并对最大变形量和一阶固有频率作了理论计算。以横梁的质量，总形变，固有频率为优化目标，通过改进横梁上下导轨局部结构，同时对优化后的横梁受力导轨面的不同位置施加相同载荷，获得横梁受力导轨面变形曲线，证明了优化设计后横梁的可靠性。

1 移动横梁变形量及一阶固有频率理论计算

横梁在左右两侧受到滚珠丝杠螺母的支撑力，在横梁上下导轨上承受滑板、主轴箱等零部件的重量(见图1)。结合机械振动学和材料力学将横梁简化成如图2所示的横梁振动力学简图。

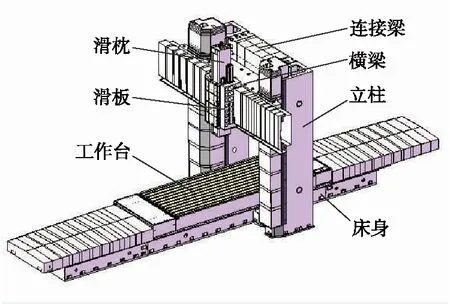
图1 龙门加工中心整机三维装配图

图2 横梁振动力学简图

振动系统的微分方程一般表达式为[6]：

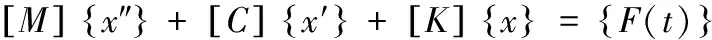
(1)

式中[M]是质量矩阵；[C]是阻尼矩阵；[K]是刚度矩阵；{x}是位移矢量；{F(t)}是力矢量；{x′}是速度矢量；{x″}是加速度矢量[6]。

对于无阻尼模态分析，其运动方程如下：

(2)

结构的自由振动为简谐振动，即位移为正弦函数：

x=xsin(ωt)

(3)

带入上式得：

(4)

根据材料力学，对于机床系统模型，距支座距离x处的位移表达式为[7]：

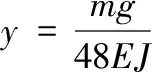
(5)

其中,ym为中点挠度，根据材料力学：

(6)

横梁动能：

(7)

式中,ρ为横梁单位长度上的质量。

因为有限元模态力学特性是以简谐振动为前提的，因此设：

ym=Asin(ωnt+φ)

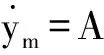
(8)

横梁系统的最大总动能为：

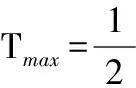
(9)

横梁最大弹性势能：

(10)

由Tmax=Umax得：

(11)

计算得：

(12)

式中,k为横梁的弹性刚度，对于简支梁中间带有集中质量时：

又因为：ωn=2πf，则：

(13)

在计算横梁固有频率时，为模拟横梁在自由状态下(无负载)的一阶固有频率，在计算时将式(12)中的m计为零计算，由式(13)得：

f=145.79Hz

由式(6)、(13)可知：横梁自重ρL和横梁系统的刚度K是影响横梁形变量和频率的主要影响因素，因此适当增加横梁的刚性和减轻横梁的质量可以减少横梁的静力学变形量，增加横梁的振动频率，从而提高横梁综合性能。

2 移动横梁有限元分析

2.1 移动横梁的建模与受力分析

由于数控龙门加工中心机构复杂，为提高分析速度和精度，在使用SolidWorks建立横梁三维实体模型时，简化无关紧要的细小结构或零件；在ANSYS Workbench中分析时，不直接把龙门加工中心整体导入进来，仅对横梁导入进行分析[8-9]。

图3 受力分析简图

如图3所示，移动横梁在底部两侧受到安装于立柱上滚珠丝杠螺母的支撑力2F1，竖直方向上受到除自身重力G外，还有滑板部件(包括滑板、滑枕、主轴箱等零部件)的总重力G1，为便于分析，将G1对移动横梁的作用效果等效为：垂直于移动横梁上导轨面与下导轨面的力F2和F3，垂直于上导轨内侧面力F4和垂直于下导轨外侧面力F5。

根据静力学公理可得：

2F1=G1+G2

(14)

滑板、滑枕、主轴箱等的重力G1在竖直方向上：

(15)

G1对O点产生的转矩等效为F4和F5对O点产生的扭矩：

(16)

根据式(14)～ 式(16)，图3中各参数取值如表1所示。

表1 各参数计算取值

2.2 移动横梁静、动态仿真分析

将已建好的移动横梁三维模型导入ANSYS Workbench中，对移动横梁进行网格划分，得到如图4所示的移动横梁有限元模型，共有节点数415985个，单元数239915个。

图4 移动横梁有限元模型

横梁的材料属性：材料为灰铸铁，密度7250kg/m3，弹性模量120GPa，泊松比0.27，环境温度设为22℃。对移动横梁施加载荷与约束时，将F1作用约束和夹紧装置作用约束转化为对应面的固定约束；为模拟横梁自重对分析结果的影响，在竖直方向上添加重力加速度1g；因滑板部件在横梁上运动时，横梁会产生不同程度的弯曲变形，而当滑板部件处于横梁中间位置时横梁产生最大的弯曲变形[2]，因此按此种情况进行施加F2、F3、F4、F5载荷，依据受力分析简图所示施加到对应的面上。分析结果如图5所示，横梁最大变形为36.109μm，一阶固有频率为138.68Hz。

由上述分析显示，横梁主要形变在上导轨面，方向主要在Y向和Z向；最大应力为4.5MPa，未超过300MPa，一阶固有频率为138.68Hz，大于横梁的激振频率(主轴转速为0～6000r/min，频率范围为0～100Hz)，不会发生共振现象。由以上分析可知：移动横梁整体应力较小，横梁主要受力位置和主要形变位置在上下导轨处，上下导轨位置结构强度较低，需对其优化以提高横梁刚性。

(a)最大变形云图

(b)一阶固有频率振型云图图5 优化前最大变形和一阶固有频率云图

2.3 求解结果分析

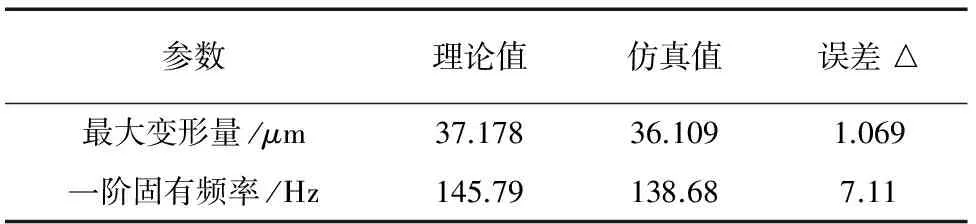
表2 理论计算与仿真分析值

由表2中数据可知：横梁最大变形量的理论值与仿真分析值非常接近，误差△=1.069μm；频率的理论计算值与仿真分析值也很接近，误差△=7.11 Hz，说明横梁系统振动力学模型的建立是合理的。误差的主要原因是：进行理论计算时，①将横梁内部箱体式筋板结构简化成空心矩形结构；②将外载荷(质量m)面力作用的效果，简化为点作用效果；③将横梁四棱柱型外形结构简化为简单的等厚度矩形截面外形结构。

3 移动横梁优化设计

3.1 横梁优化设计

根据横梁静态分析结果，选择横梁上下导轨支撑筋板作为设计变量，以横梁总形变最小及重量最小为目标函数。在优化设计分析过程中，保证优化前与优化后的横梁所施加的载荷与约束相同。

如图6所示，因滑板部件位于横梁中间位置时，横梁形变最大，为提高横梁刚性，将横梁上导轨部位的下支撑筋板设计成45°倾斜状；将横梁下导轨部位的上支撑筋板设计成45°倾斜状。

(a)优化前 (b)优化后图6 横梁优化前后对比图

图7所示。为优化前后横梁上导轨力学分析简图及其剪力和弯矩图。力学平衡方程：

(a)优化前 (b)优化后图7 上导轨力学模型及剪力和弯矩简图

由以上分析可知优化后横梁上导轨面在竖直方向上受力减少了Fy'，弯矩减小了Fy'l。因下导轨支撑筋板设计与上导轨类似，这里不做具体介绍。

3.2 横梁优化结果分析

对优化后的横梁模型进行有限元分析，对比优化前后滑板部件位于横梁中间位置时的有限元分析主要性能参数，如表3所示，优化后横梁形变总位移减小了10.6%，质量减轻了136kg，一阶固有频率也有所增加，X、Y、Z轴向形变均有减少，且Y向形变降低幅度最大，降幅达13.1%，说明优化后横梁的整体刚度有所提高，轻量化效果明显。

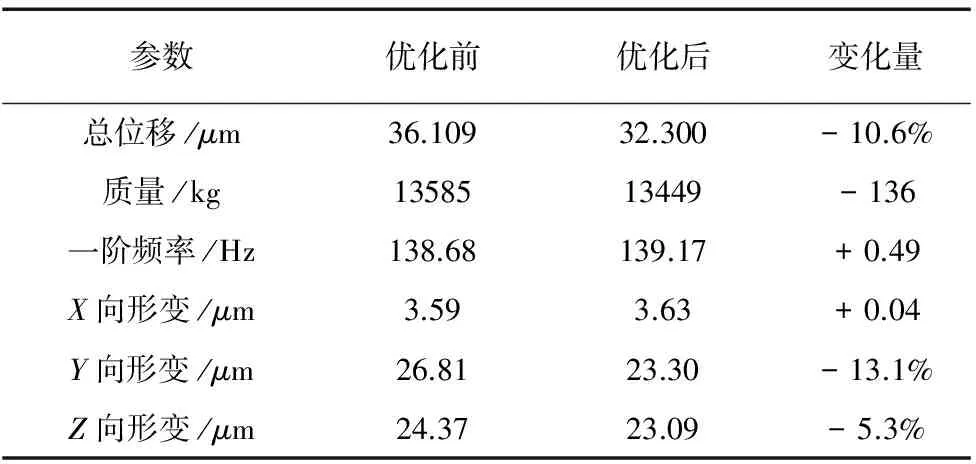
表3 优化前后主要参数

注：“+”表示增加，“-”减少。

横梁各阶振型频率与振幅如表4所示，可以发现，在振幅基本不变的情况下，优化后横梁的前6阶固有频率均有所提高，且均大于机床最大激振频率(机床主轴转速为0～6000r/min，主轴对横梁的激振频率为0～100Hz)[10]，说明横梁的优化设计是合理的。

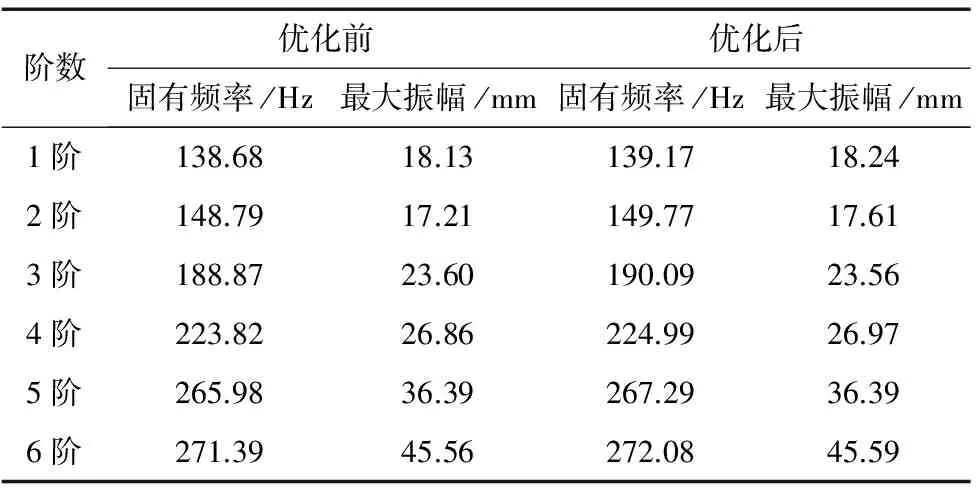
表4 各阶振型参数

图8 优化前后横梁形变情况

为对比优化前后横梁其他位置的变形情况，分别对优化前后横梁滑板部件位于横梁不同位置时的静态特性进行分析。因该横梁滑板在横梁上的行程为3700mm，因此从距横梁左侧1200mm处开始取受力面中心，依次每间隔200mm进行不同位置的静态特性有限元分析，取至距横梁左侧4.8m处为止。分析出的横梁总变形曲线图如图8所示，优化前后横梁最大形变位置均位于横梁中间位置，并且向横梁两侧随着距离的增大形变逐渐减小，优化后横梁形变减小明显。

4 结论

(1) 对横梁进行结构简化并建立振动力学模型，理论计算原横梁的最大变形量和一阶固有频率，其结果与仿真结果相近。通过优化设计横梁外形结构，对比优化前后横梁静、动态特性，优化后的横梁中间薄弱位置总变形减小了10.6%，y向形变减少了13.1%，横梁整体质量减轻了136kg，一阶固有频率也有所增加，横梁整体刚性得到了提高，取得了良好的轻量化效果。证明了该优化设计方法的合理可性，为其它零部件优化设计提供了借鉴方法。

(2) 文中仅对横梁上下导轨处的结构进行了设计与改进，从而达到提高横梁刚性及轻量化效果。若对横梁内部筋板结构(井字形，口字形，X形，等)进行设计与分析，以及针对横梁变形问题采取相应的补偿措施，将进一步优化横梁结构与性能，这将作为今后的研究方向。

[1] 王晓煜, 贾振元, 杨帆, 等. 龙门加工中心横梁的拓扑优化设计与分析[J]. 制造技术与机床, 2009(11):64-68.[2] 许丹, 刘强, 袁松梅. 一种龙门式加工中心横梁的动力学仿真研究[J]. 振动与冲击, 2008, 27(2):168-172.

[3] 周乐, 袁军堂, 汪振华. 龙门式机床横梁筋板结构分析与优化[J]. 机械设计与制造, 2014(1): 15-17.

[4] Shihao Liu, Wenhua Ye, Peihuang Chen, et al. Bionic design for column of gantry machining center to improve the static and dynamic performance[J]. Shock and Vibration, 2012(19): 493-504.

[5] SOROKIN S V, NIELSEN J B, OLHOFF N. Analysis and Optimization of Energy Flows in Structures Composed of Beam Elements [J]. Structure Multidisc Optim, 2001(22): 12-33.

[6] 丁欣硕, 凌桂龙. ANSYS Workbench 14.5有限元分析案例详解[M]. 北京: 清华大学出版社, 2014.

[7] 张义民. 机械振动[M]. 北京: 清华大学出版社, 2007.

[8] 王宇清, 曹忠亮. 大型铣床横梁模态分析及装配改进方法研究[J]. 制造技术与机床, 2014(9):137-139.

[9] 朱金波, 王宇, 阳红, 等. 基于转移质量方式的龙门加工中心动横梁结构优化设计方法[J]. 机械设计与制造, 2012(9):37-39.

[10] 季彬彬, 张森, 杨玉萍, 等. GMF3022龙门加工中心横梁的模态及谐响应分析[J]. 组合机床与自动化加工技术, 2013(10):36-39.

(编辑 李秀敏)

Static and Dynamic Characteristics Analysis and Structure Improvements for Moving Crossbeam of Gantry Machining Center

JU Jia-quan1, REN Dong2, CUI De-you2, LIU Chuan-jin2, QIU Zi-xue1

(1.School of Mechanical Engineering, Nantong University, Nantong Jiangsu 226019, China;2. Nantong Guosheng Electromechanical Group Company Ltd., Nantong Jiangsu 226003, China)

The deformation of moving beam is caused by its own gravity and the loads. Therefore, The crossbeam was simplified to get the mechanical vibration model，the maximum coupling deformation and the first-order frequency were solved by the theoretical calculation method. Through establishing its 3D model and finite-element analysis, which shows that the most vulnerable position is the upper and lower guide rail. To the weakest part, the local structure of ribbed plate on the upper and lower guide rail was designed. The results show that, Theoretical analysis and simulation results are very similar. Compared with the original beam, the lightweight effect is obvious that the beam deformation is decreased by 10.6%, the weight is reduced by 136 kg, which proved a reasonable method for other parts of machine tool.

gantry machining center; crossbeam; optimization design; lightweight; finite element analysis

1001-2265(2017)01-0004-05

10.13462/j.cnki.mmtamt.2017.01.002

2016-03-04 ;

2016-04-13

江苏省产学研前瞻性联合研究项目(BY2015047-11)；南通市重大科技创新专项(XA2014011)

鞠家全(1990—)，男，江苏淮安人，南通大学硕士研究生，研究方向为机电装备及测控技术，(E-mail)1183559116@qq.com；通讯作者：邱自学(1963—)，男，江苏南通人，南通大学教授，博士生导师，研究方向为机电装备及测控技术，智能结构及其健康监测技术，(E-mail)nqiuzx@163.com。

TH122;TG502

A