基于粒子群算法的机床支承件不确定性多目标优化*
2017-02-15马雅丽
马雅丽,徐 涛,钱 峰
(大连理工大学 机械工程学院,辽宁 大连 116024)
基于粒子群算法的机床支承件不确定性多目标优化*
马雅丽,徐 涛,钱 峰
(大连理工大学 机械工程学院,辽宁 大连 116024)
考虑支承件材料密度、弹性模量以及切削载荷的不确定性,提出基于不确定性分析的支承件多目标优化设计方法。以某型号机床主轴箱为例,基于灵敏度分析方法选取对切削点位移和主轴箱重量影响较大的特征尺寸作为优化变量;以支持向量机方法构建切削点位移、主轴箱重量和主轴箱一阶固有频率的近似模型;基于稳健性考虑建立优化问题目标函数,以主轴箱固有频率为约束,利用粒子群算法对此多目标优化问题进行优化。优化结果在满足设定频率要求的前提下,得到切削点位移减小和主轴箱重量减轻的最优解集。
不确定性;多目标;近似模型;粒子群算法
0 引言
为保证机床精度,支承件设计需满足各项性能指标。采用传统的经验法和相似产品类比法设计机床支承件,效果远达不到预期要求,且设计周期长、效率低[1-2]。支承件设计制造过程中存在的各种不确定性因素,更使得传统设计方法无法满足现代高精度机床的设计要求。因此在不确定性因素影响下,研究支承件满足多性能需求的多目标优化设计,成为机床设计的一个重要方向。
不确定性多目标优化方法可在充分考虑各不确定因素的情况下,使设计的各项性能指标达到预期水平,因此也越来越多地被用来解决实际问题。VoβT等[3]针对进化多目标优化中存在噪声的问题,提出了一种新的稳健选择策略。Tenerelli P等[4]提出一种多标准、多目标和不确定性分析的方法来评估能源作物转换的一系列可能性。Cardona-Valdés Y等[5]提出基于客户需求不确定性的双目标供应链设计方法。
常规有限元方法无法解决由于不确定因素引入带来的不确定性建模问题,也无法提供用于不确定性多目标优化的算法。本文以某型号机床主轴箱为例,根据主轴箱特征尺寸对刚度、重量的灵敏度分析选取优化变量;利用支持向量机方法建立主轴箱的近似模型;利用一阶固有频率作为约束,保证主轴箱的动态性能;采用粒子群算法求解主轴箱不确定性多目标优化问题。
1 主轴箱不确定性多目标优化问题
支承件主要性能评价指标有静刚度、重量和动态性能,因此本节就如何建立旨在提高支承件各项性能的不确定性多目标优化问题进行了阐述。
基于粒子群算法求解立足不确定性多目标优问题的流程如图1所示。

图1 主轴箱不确定性多目标优化设计流程
1.1 不确定性多目标优化问题描述
考虑不确定因素影响的支承件多目标优化问题不同于常规多目标优化问题。本文以支承件切削点位移和支承件重量为目标,以支承件一阶固有频率为约束,建立目标函数和约束函数都包含不确定变量的不确定性多目标优化问题。则带约束的支承件不确定性多目标优化问题可描述为:

1.2 不确定性多目标优化问题转化
在不确定因素的影响下,机床切削点位移、主轴箱重量和主轴箱一阶固有频率也会是区间值,这里采用其区间中点值来衡量支承件性能的优劣:
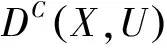


考虑到静刚度稳健性会对主轴箱性能产生深刻影响,此处计入切削点位移波动区间大小,则主轴箱不确定性多目标优化问题最终转化为:

1.3 基于粒子群算法的不确定性多目标优化
不确定性多目标优化问题属于复杂的嵌套优化问题。这就要求优化算法需能精确求解优化目标不确定区间、且求解速度快。为此,本文选用粒子群算法进行主轴箱不确定性多目标优化问题求解。
粒子群算法作为一种较新的智能算法,以其全局搜索能力强和求解速度快的特点[6-7],被越来越多的应用到求解多目标优化问题。粒子群算法优化过程中,个体粒子会以自身的飞行经验以及群体的飞行经验来调整飞行速度。假设一个群落由m个粒子组成,第i个粒子位置为xi,速度为vi,i=1,2…,m。其个体搜索到的历史最优位置为pbesti,整个群落搜索到的历史最优位置为gbesti,则第i个粒子演化公式如下:

其中:w为惯性权重,c1和c2为加速系数。
为加强不确定性多目标优化算法的全局搜索能力,本文采用加入max-min(最大最小)适应度函数的改进多目标粒子群算法来对主轴箱不确定性多目标优化问题进行优化,该算法能够提高非劣最优解集的分散程度。算法中第i个粒子u(设该种群有N个粒子)的max-min适应值求解过程如下:首先求解粒子u和其他粒子在m个目标函数差值的最小值:
然后上述集合中最大值作为粒子u的max-min适应值:
2 主轴箱支持向量机模型建立
采用粒子群算法对主轴箱不确定性多目标优化问题进行优化,若每次都调用有限元软件求解优化目标,求解效率会非常低,因此建立高效的近似模型来代替有限元模型成为了解决这一问题的有效途径。
支持向量机(SVM)作为近年来发展迅速的近似建模方法,其在实际工程问题中国应用越来越广泛[8]。非线性支持向量机是在线性支持向量机基础上加入核函数得到的。支持向量机算法的核心思想是:利用核函数将样本数据映射到特征空间中;按照样本点在特征空间中距离近似超平面的大小排序;将离近似超平面最近的一定量的样本与本次近似超平面的支持向量构成新的训练样本;以上述训练样本构建新的近似超平面;如此循环往复,最终得到所有支持向量。支持向量机模型记为:

利用支持向量机方法建立主轴箱近似模型,需要首先确定不确定性多目标优化问题的优化变量和不确定变量。
2.1 不确定变量的选取
支承件不确定性多目标优化问题中不确定变量的选取影响设计结果的可靠程度,按照不确定因素对支承件性能影响大小选取不确定变量,在此基础上的设计将会表现出良好的稳健性。
支承件材料属性与支承件重量、机床切削点位移和支承件固有频率密切相关,机床切削载荷更是直接影响着切削点位移大小,选取主轴箱材料密度、弹性模量及切削载荷为不确定变量。铸铁密度不确定区间参考钢铁材料手册取值;铸铁弹性模量依据文献[9]计算得到;切削载荷依据机床典型工况,并参考文献[10]划定变化区间,所有不确定变量及其变化区间见表1。

表1 不确定变量变化区间
2.2 基于灵敏度分析选取优化变量
选取对优化目标(切削点位移、主轴箱重量)灵敏度较高的主轴箱特征尺寸,作为主轴箱多目标优化问题的优化变量。
建立如图2所示主轴箱三维模型,选取主轴箱主要外形尺寸、主要壁板尺寸和主要筋板尺寸作为灵敏度分析参数,分别有侧壁板厚P1、水平壁板厚P2、隔板厚P3、主轴支承孔壁厚P4、筋板厚P5和筋板宽P6。

图2 主轴箱三维模型
将切削点位移和主轴箱重量作为灵敏度分析的评价指标,利用ANSYS workbench软件建立6个灵敏度分析参数与评价指标间的灵敏度分析模型,最后输出灵敏度分析柱状图(见图3)。

图3 特征尺寸灵敏度柱状图
图3中分别表示特征尺寸对切削点位移和主轴箱重量的灵敏度大小。由图可以看出侧壁板厚P1、水平壁板厚P2、隔板厚P3对切削点位移和主轴箱重量的灵敏度比较高。因此选取这3个特征尺寸作为主轴箱不确定性多目标优化问题的优化变量,分别为主轴箱侧壁板厚、水平壁板厚、隔板厚,其取值区间见表2。其他为选为优化变量的特征尺寸则按照各自灵敏度高的评价指标达到最高时的尺寸圆整得到(主轴支承孔壁厚P4为10mm,筋板厚P5为23mm,筋板宽P6为66mm)。

表2 优化变量区间
2.3 支持向量机模型建立过程及其精度验证
采用拉丁超立方试验方法有效减少采样数量,最大化数据利用率,以此建立支承件近似模型。支持向量机模型建立过程如下:
首先,将拉丁超立方试验设计方法得到的优化变量和不确定变量的300组设计点,使用ANSYS Workbench中进行非线性有限元计算,得到相应的切削点位移D、主轴箱重量M和一阶固有频率f1;利用支持向量机方法构建设计变量和不确定变量与切削点位移D、主轴箱重量M和一阶固有频率f1的SVM模型;再次随机抽取抽取3组对比点,将其有限元模型计算值和SVM模型计算值对比,若误差在允许范围内,则证明近似模型符合要求。
表3给出主轴箱切削点位移、主轴箱重量和一阶固有频率的SVM模型计算值与有限元模型计算值进行对比,并求得误差,可以看出其误差都在1.5%以内,以此可证明SVM模型精度达到要求。

表3 主轴箱有限元模型与SVM模型对比表
3 求解结果分析
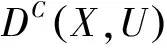

图4 Pareto最优解集
相对于优化前主轴箱(切削点位移均值5.26μm,位移区间0.78μm,重量233.8kg),选取图4中重量在220kg附近的最优解,切削点均值可降至4.59μm,位移区间降至0.62μm,重量降至215.8kg。由此可看出,优化后的主轴箱各项性能均有了比较明显的提升。

图5 最优解集的一阶固有频率
4 结论
本文考虑支承件材料属性和切削载荷的不确定性,采用支持向量机方法解决了有限元方法无法建立不确定优化模型的问题。运用改进的嵌套粒子群算法对加入一阶固有频率约束的主轴箱不确定性多目标优化问题进行求解。优化后的主轴箱,在保证固有频率不低于原模型的情况下,刚度提高14.6%,稳健性提升25.8%,质量降低8.3%。
[1] Ma Ya Li, Gong Zhen, Ma Chao. Structure Design of a Machining Center Bed Based on Topology Opti-mization Technique[J]. Applied Mechanics & Mat-erials, 2014, 490-491:580-585.
[2] 马雅丽, 赵二鑫, 赵宏安,等. 拓扑优化的数控车削中心床鞍轻量化设计[J]. 机械设计与研究, 2011,27(3):103-107.
[3] Voβ T, Trautmann H, Igel C. New Uncertainty Handling Strategies in Multi-objective Evolutionary Optimization[J]. Lecture Notes in Computer Science, 2010, 6239:260-269.
[4] Tenerelli P, Carver S. Multi-criteria, multi-objective and uncertainty analysis for agro-energy spatial modelling[J]. Applied Geography, 2012, 32(2): 724-736.
[5] Cardona-Valdés Y, álvarez A, Ozdemir D. A bi-objective supply chain design problem with uncertainty[J]. Transportation Research Part C Emerging Technologies, 2011, 19(5):821-832.
[6] Frans V D B, Engelbrecht A P. A Cooperative approach to particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3):225-239.
[7] Cheng S, Shi Y. Diversity control in particle swarm optimization[C]// Proceedings of the 7th International Conference on Evolutionary Programming VII. Springer-Verlag, 2011:591-600.
[8]丁世飞,齐丙娟,谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报,2011,40(1):2-10.
[9] 宋晓东. 杨氏模量不确定度的评定方法[J]. 吉林建筑工程学院学报, 2009,26(5):100-102.
[10] Wang W P, Peng Y H, Li X Y. Fuzzy-grey prediction of cutting force uncertainty in turning[J]. Journal of Materials Processing Technology, 2002, 129(s 1-3):663-666.
(编辑 李秀敏)
Machine Tool Support Uncertainty Multi-objective Optimization Based on Particle Swarm Optimization Algorithm
MA Ya-li,XU Tao,QIAN Feng
(School of Mechanical Engineering,Dalian University of Technology, Dalian Liaoning 116024, China)
A machine tool support multi-objective optimization method based on uncertainty analysis has been proposed, in which the uncertainty of support density, modulus and cutting loads are considered. A case study on a particular type of machine tool spindle box has been carried out using this method. First, the optimization variables are selected out based on the sensitivity analysis of spindle box feature sizes relative to the cutting point displacement and the column weight. Then the approximation models of cutting point displacement, spindle box weight and spindle box first inherent frequency are established. Next, the objective function of the optimization problem is built by considering robustness, with the spindle box first inherent frequency as the constraint. By adopting particle swarm optimization algorithm, the spindle box multi-objective optimization problem is solved. Finally, the optimal solution set of cutting point displacement decreasing and spindle box weight losing is obtained which satisfies the given frequency request.
uncertainty; multi-objective; approximation model; genetic algorithm
1001-2265(2017)01-0001-03
10.13462/j.cnki.mmtamt.2017.01.001
2016-05-04;
2016-05-18
国家科技重大专项(2015ZX04005002);国家科技重大专项(2015ZX04014-021-03)
马雅丽(1963—),女,辽宁鞍山人,大连理工大学副教授,博士,研究方向为机械设计理论与方法,(E-mail)myl@ dlut.edu.cn;通讯作者:徐涛(1989—),男,满族,山东青岛人,大连理工大学硕士研究生,研究方向为机床结构设计,(E-mail)xutao4412008@163.com。
TH122;TG506
A
