不同续航里程动力辅助系统启停控制优化

林歆悠 张少博 冯其高福州大学机械工程及自动化学院,福州,350002

不同续航里程动力辅助系统启停控制优化

林歆悠 张少博 冯其高
福州大学机械工程及自动化学院,福州,350002

针对某款增程式电动车，为满足不同负荷功率需求，制订了多点能量管理策略，以油耗最小为目标构建了动力辅助系统(APU)启停控制优化模型，以性能指标和电池循环寿命为约束，优化了不同工况不同行驶里程的APU启停控制参数，实现了续航里程自适应APU启停控制。结果表明：与优化前油耗相比，NEDC100/NEDC200、CUDC100/CUDC200分别减少15.87%/2.09%、42.24%/14.54%。对比优化前后能量消耗，得到同里程下减少油耗方式：单一负荷下，缩短APU工作时间；不同负荷情况下，延长中低负荷下工作时间，从而缩短高负荷下工作时间。

增程式电动车；续航里程；动力辅助系统；启停控制

0 引言

由于能源危机，汽车制造商很早就出于家用或商用的目的，致力于纯电动汽车的性能改善。然而，与传统内燃机汽车相比，有限的里程仍然是它不可逾越的障碍。统计研究表明，纯电动汽车单次充电可以满足90%的日常行驶需求[1-2]。但是，用户在遇到偶尔超出电动车可用行驶里程或恰好在电池无电可用但需要使用情况下，纯电动汽车就会显得“束手无策”。此外，在现有电池技术条件下，环境因素将严重影响纯电动汽车的行驶里程，低的室外温度条件下，电动汽车行驶里程几乎缩水20%。这些因素都使得增程式电动车(range-extended electric vehicle，R-EEV)成为目前的研究焦点[3]。

由于增程式电动车可以从发电机组和外接电网获得电能，故它被归类为插电式串联混合动力汽车。混合动力汽车能量管理策略的目标主要是在满足车辆性能的条件下，通过有效的模式切换和能量分配使得燃油经济性最优，可以将其归纳为基于直观逻辑规则和基于优化算法两类。

基于规则的控制策略由于简单易行被广泛应用。文献[4]针对非线性的插电式串联混合动力汽车系统，利用模糊逻辑建立了基于规则的能量管理策略，但是这些规则不适用于多变量的复杂系统。文献[5]针对一款增程式电动车，在研究发动机定点能量管理策略的基础上，以燃油经济性为目标对增程器的开关时刻进行了优化，没有考虑负荷的变化对需求功率的影响。文献[6]也是针对定点能量管理策略，研究了通过缩短定里程下发动机工作时间来减少油耗，但对于多点能量管理策略而言，发动机工作时间最短并不意味着燃油消耗最少。为此，通过研究特定里程下，多点工作模式下动力辅助系统的启停对油耗的影响，分析影响油耗的因素，建立油耗与其影响因素之间的关系成为需要解决的关键问题。

对于优化算法的控制策略，在解决全局最优问题中，动态规划和最小值原理是优化算法中常用的方法，但是动态规划常遭遇“维数灾难”[7]。最小值原理涉及在边界约束下解复杂的哈密顿函数[8]。等效燃油消耗最小控制策略作为瞬时优化算法，并不能保证全局最优[9]。文献[10]利用改善的粒子群优化(PSO)算法构建了三输入(转速、电池荷电状态(SOC)、需求转矩)单输出(能量分配系数)的次优能量管理模型。文献[11]利用PSO算法来设计插电式混合动力汽车控制参数，以燃油经济性为适应度函数，在不牺牲动力性的条件下，改善了燃油经济性，并研究优化后的控制参数在不同工况下的表现。文献[12]通过PSO算法优化动力系统参数和控制策略参数，从而减少油耗、排放和降低混合动力汽车(HEV)的制造成本。

本文基于动力辅助系统多点工作模式控制策略，研究了各负荷点的工作时间、油耗、启停次数随动力辅助系统启停阀值SAPU_strat和SAPU_off的变化，来建立油耗和行驶里程L、负荷P、SAPU_strat和SAPU_off之间的关系,从而构建四输入单输出的适应度函数模型。以油耗最小为目标建立优化模型，以性能指标和电池寿命为约束，利用PSO算法优化不同工况不同行驶里程下的动力辅助系统(APU)启停控制参数，以此实现里程自适应APU启停控制。

1 R-EEV动力系统

如图1所示，增程式电动车动力系统主要包括动力电池组、APU、电机驱动系统和动力传动系统。

增程式电动车与串联式混合动力汽车的动力系统结构类似，但是与串联式不同的是增程式电动车的动力电池为主能源，发动机只用于发电，不直接参与汽车驱动。增程式电动汽车有两种工作模式：①纯电动模式(EV)，电量充足时，发动机不工作，驱动电机由动力电池提供能量，也可称作电量消耗阶段;②增程驱动模式(RE)，当电量消耗至低于阀值时，APU启动,提供的电能一部分用于驱动，另一部分为动力电池充电,当电量恢复至充足时，发动机又停止工作，继续由电池为电机驱动提供能量,也可称作电量保持阶段。增程式电动车的能量流动如图1箭头所示。图1中，VCU表示整车控制器；CAN表示控制器局域网络；EMS表示发动机控制系统；BMS表示电池管理系统；ISG电机为启动/发电一体化电机。

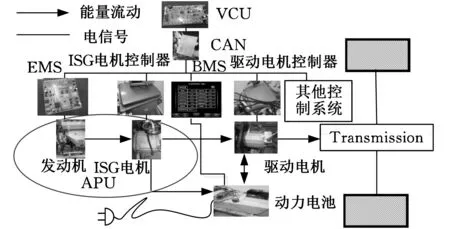
图1 R-EEV动力系统结构及能量流动Fig.1 Power-train and energy flow of R-EEV

1.1 R-EEV动力性指标

以某款R-EEV为原型车，其性能指标如表1所示，性能指标直接决定动力系统参数的匹配。

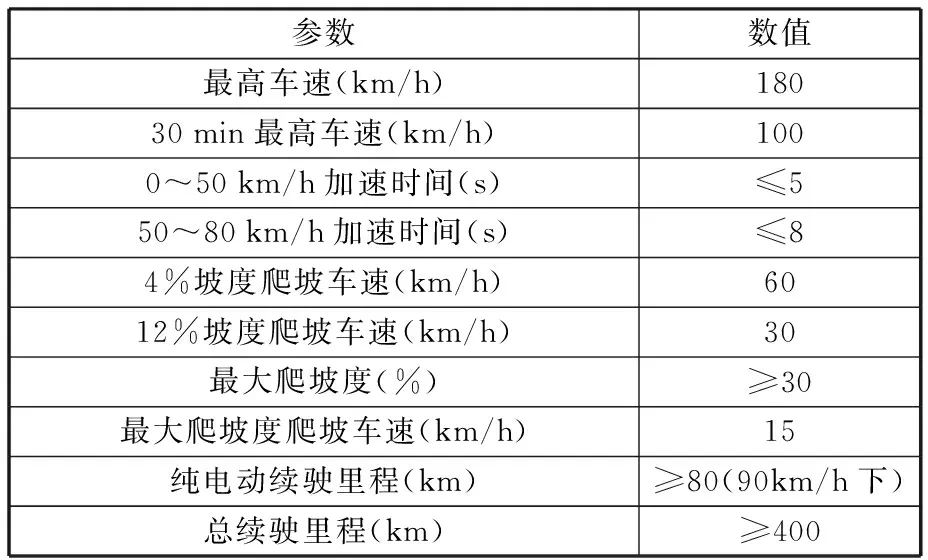
表1 某款R-EEV性能参数Tab.1 Performance parameters for R-EEV

1.2 动力电池模型

动力电池组作为R-EEV的主能源，根据性能指标匹配的磷酸铁锂电池如表2所示。采用内阻模型来计算电池荷电状态S，开路电压Voc(S，T)主要与S和温度T有关，等效内阻Rb通过试验获得。S的精确计算是能量管理的基础[13]。回路电流的计算公式为

(1)

式中，Pb为电池功率。

则SOC随时间的变化如下：

(2)

式中，Sinit为初值；Qmax为电池总容量，A·h。

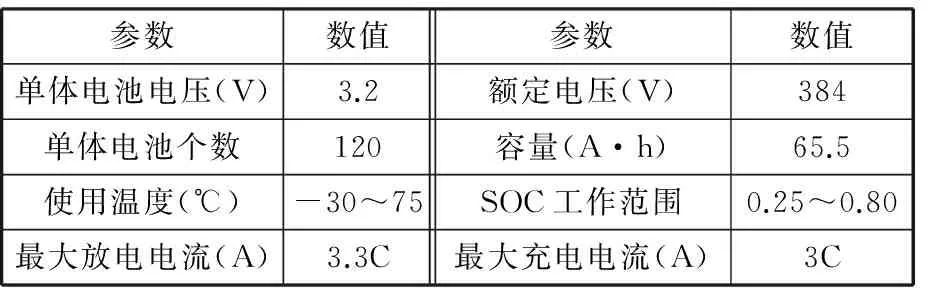
表2 磷酸铁锂电池主要参数Tab.2 Main parameters of phosphoric acid iron battery

1.3 动力辅助系统模型

APU作为延长车辆里程的辅助能源，是R-EEV关键部件之一，参数匹配结果如表3所示，发动机的万有特性曲线如图2所示。图中线条上大于100的数据表示燃油消耗率，单位为g/(kW·h)；小于100的数据表示发动机功率，单位为kW。

表3 APU工作参数Tab.3 Operational parameters of APU

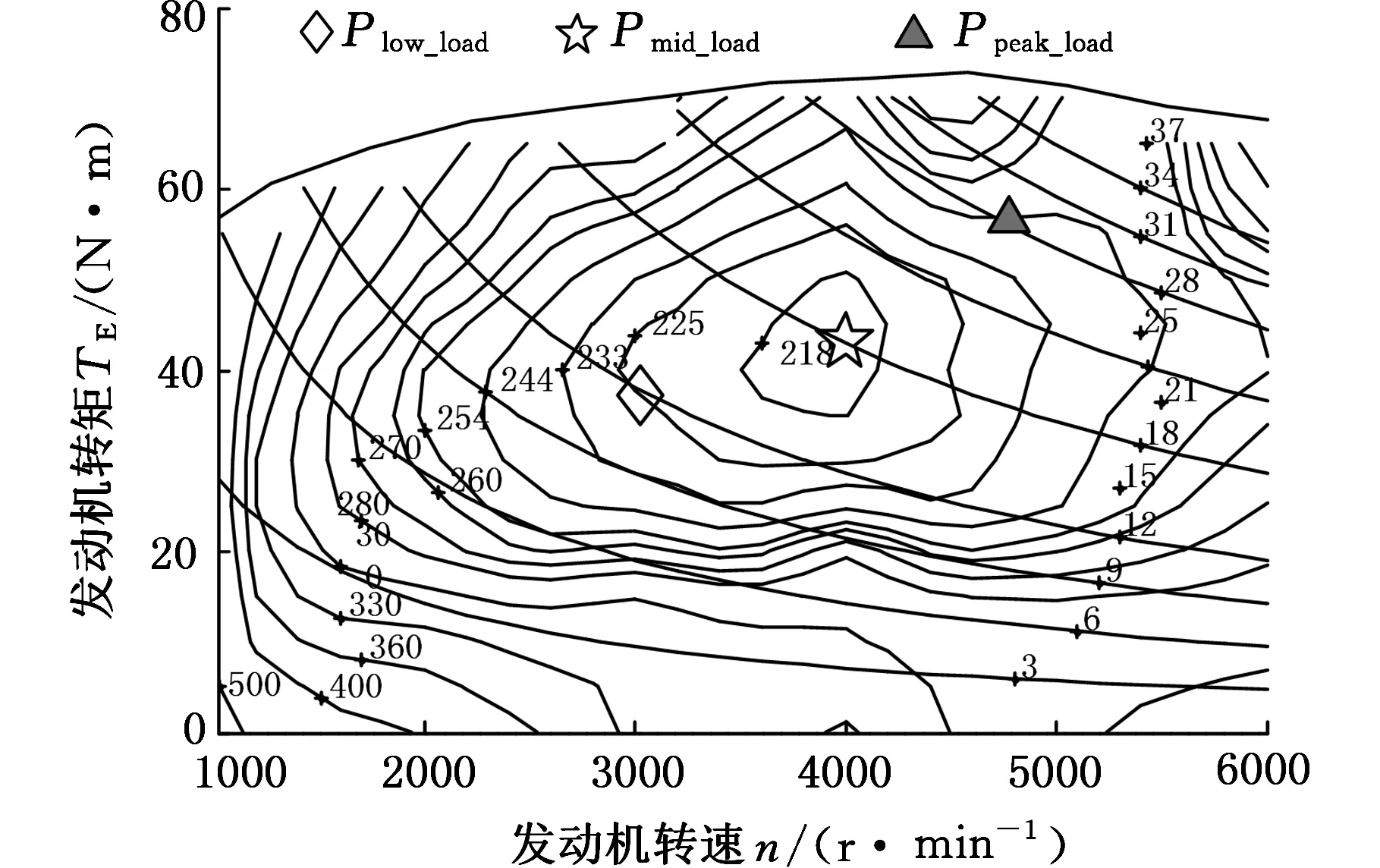
图2 发动机万有特性曲线Fig.2 The map of engine fuel consumption characteristics

2 基于不同里程的APU启停控制

2.1 APU多点工作模式控制策略

文献[14]采用人工智能算法来预估电动汽车的纯电动行驶里程，但是由于计算量大，这些方法在增程式电动车的纯电动里程预测时可行性变差。文献[15]针对插电式混合动力汽车纯电动行驶里程预测提出了三种简单模型：基于牛顿力学的物理模型、能量模型和SOC模型。本文采用SOC模型对增程式电动车的纯电动续航里程进行预先估计，其续航里程和SOC的关系可表示如下：

(3)

式中，S0为当前初始电池荷电状态；SAPU_start为增程器开启时的SOC值；h为电池的健康状况表征值；Lrange0为电池额定容量下的某工况下最大纯电行驶里程；Lrange为由初始S0决定的某工况下纯电行驶里程。

R-EEV开始启动时，驾驶员设定目标行驶里程L, VCU根据目标行驶里程L进入到数据库中，选择事先存储的与之对应的控制策略参数，并根据BMS提供的初始S0计算电池能够支持的纯电里程Lrange。

VCU根据转速传感器的信号计算实时行驶里程L(t)。当L(t)小于Lrange时，增程式电动汽车相当于纯电动汽车，APU不参与工作；当行驶里程大于Lrange时，APU介入。为满足不同负荷功率需求，采取多点能量管理策略，其控制逻辑流程如图3所示。其中SAPU_start为APU开启时SOC；SAPU_off为APU关闭时SOC值;Sload为功率点切换判定SOC值;车速vhigh和vlow将需求功率分为Plow_load、Pmid_load和Ppeak_load。考虑到城市工况车速和高速工况车速，三个APU工作点如图2所示，分别为12 kW、18 kW、30 kW。

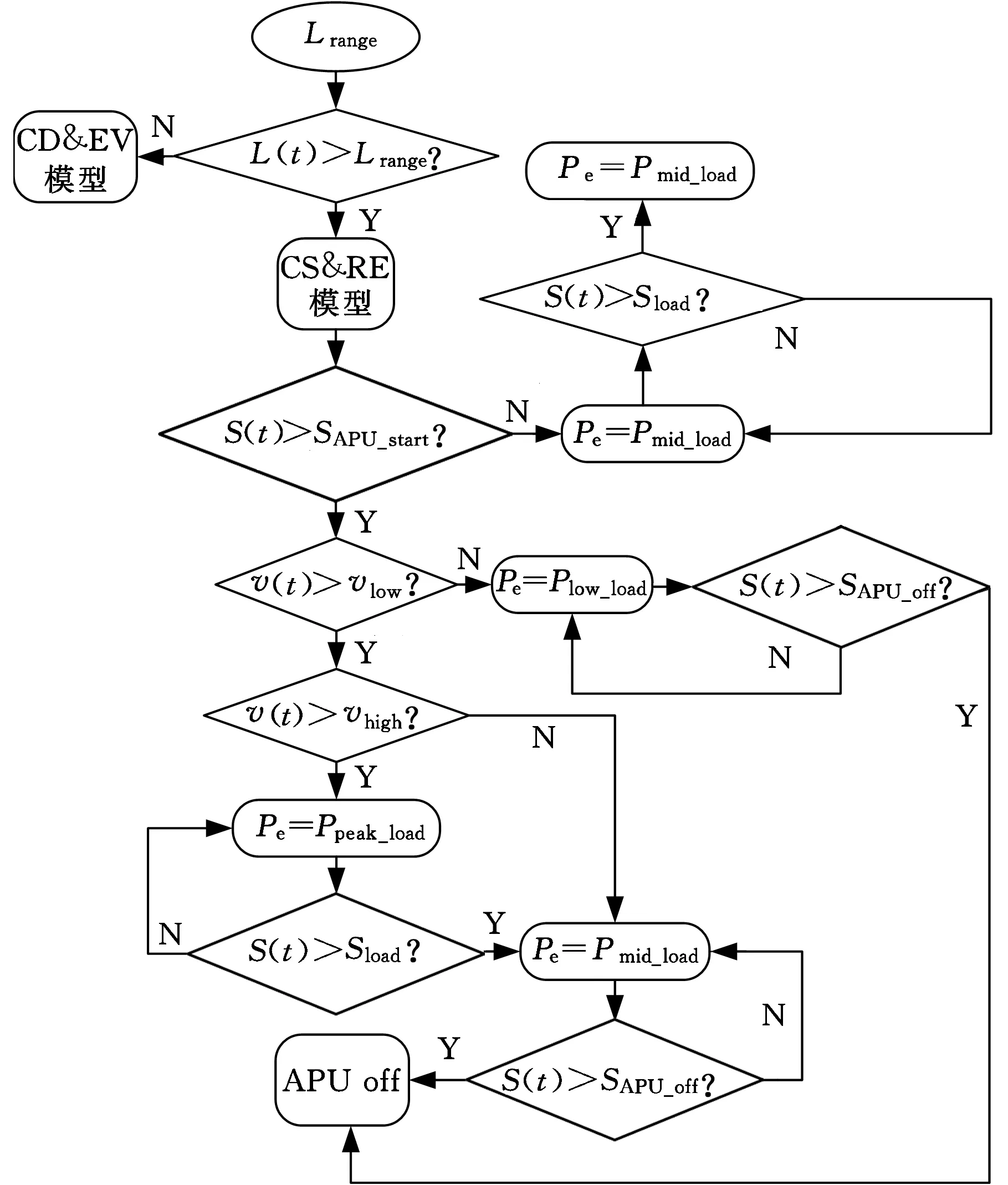
图3 APU多点工作模式控制策略流程图Fig.3 The flow chart of APU multi point working model

2.2 多点控制策略的示例验证

为了验证上述所制订的多点能量管理策略，基于Simulink建立增程式电动汽车仿真模型，采用中国轻型车辆城市工况CUDC来验证相同工况相同行驶里程(400 km)不同APU启停控制策略下的能量消耗，其结果如图4和图5所示。结果表明，不同的APU启停策略将会影响增程器的工作方式，进而影响油耗。

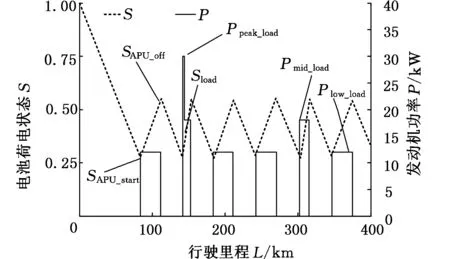
图4 APU启停方式一的能量消耗Fig.4 Energy consumption of method 1 of APU start-stop

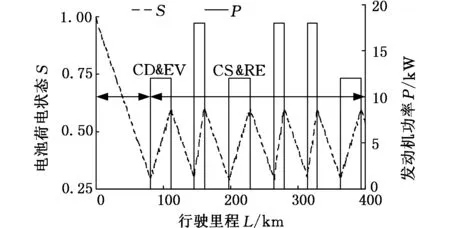
图5 APU启停方式二的能量消耗Fig.5 Energy consumption of method 2 of APU start-stop

3 不同里程APU启停控制优化

由于上述相同里程不同APU启停方式将影响发动机的工作方式，所以有必要构建APU启停控制优化模型，寻求特定里程下的最优启停方式，使得车辆能够根据续航里程自适应改变APU启停方式，从而达到节油的目的。

3.1 构建APU启停控制优化模型

假设电池满电，不断改变SAPU_start，固定SAPU_off为0.55，并使基于多点能量管理策略Simulink R-EEV模型在NEDC循环工况下运行200 km，得到燃油消耗和APU启停次数随SAPU_start变化情况，以及各负荷点工作时间。

由图6和图7可知，随SAPU_start的增大，APU启停次数逐渐增大，燃油消耗呈现非线性增加。SAPU_start由0.25增加到0.28过程中，低负荷功率点没有参与工作，中等负荷工作时间逐渐延长，高负荷功率点工作时间逐渐缩短。由于中等负荷点燃油消耗率最小，高负荷电功率点最高，所以燃油消耗在0.28时达到最小；至0.29时，中等负荷和高负荷都不参与工作，低负荷工作时间大量延长，使得油耗发生突变；达到0.3时，中等负荷参与工作，使得油耗减少；之后油耗呈现不规则周期性变化。

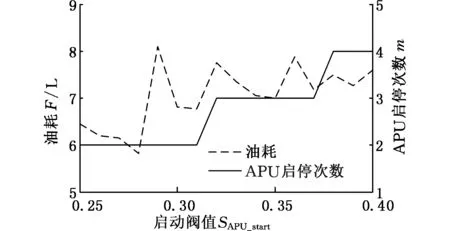
图6 APU启停次数和油耗随SAPU_start变化Fig.6 Change of APU start-stop times and fuel consumption with the change of SAPU_start

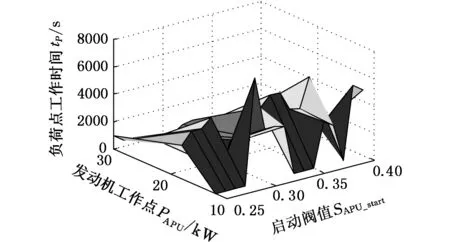
图7 各负荷点工作时间随SAPU_start变化Fig.7 Change of working time of each load point with the change of SAPU_start

相同电池状态和行驶里程条件下，固定SAPU_start为0.28，改变SAPU_off得到油耗和启停次数随SAPU_off变化情况，以及各个负荷点的工作时间。

由图8可知，在SAPU_off为0.54和0.8时，油耗相对较低。SAPU_off由0.45增加到0.8过程中，APU启停次数逐渐减少，油耗呈不规则周期性变化。不同于单点控制策略，APU启停次数和油耗没有线性关系。

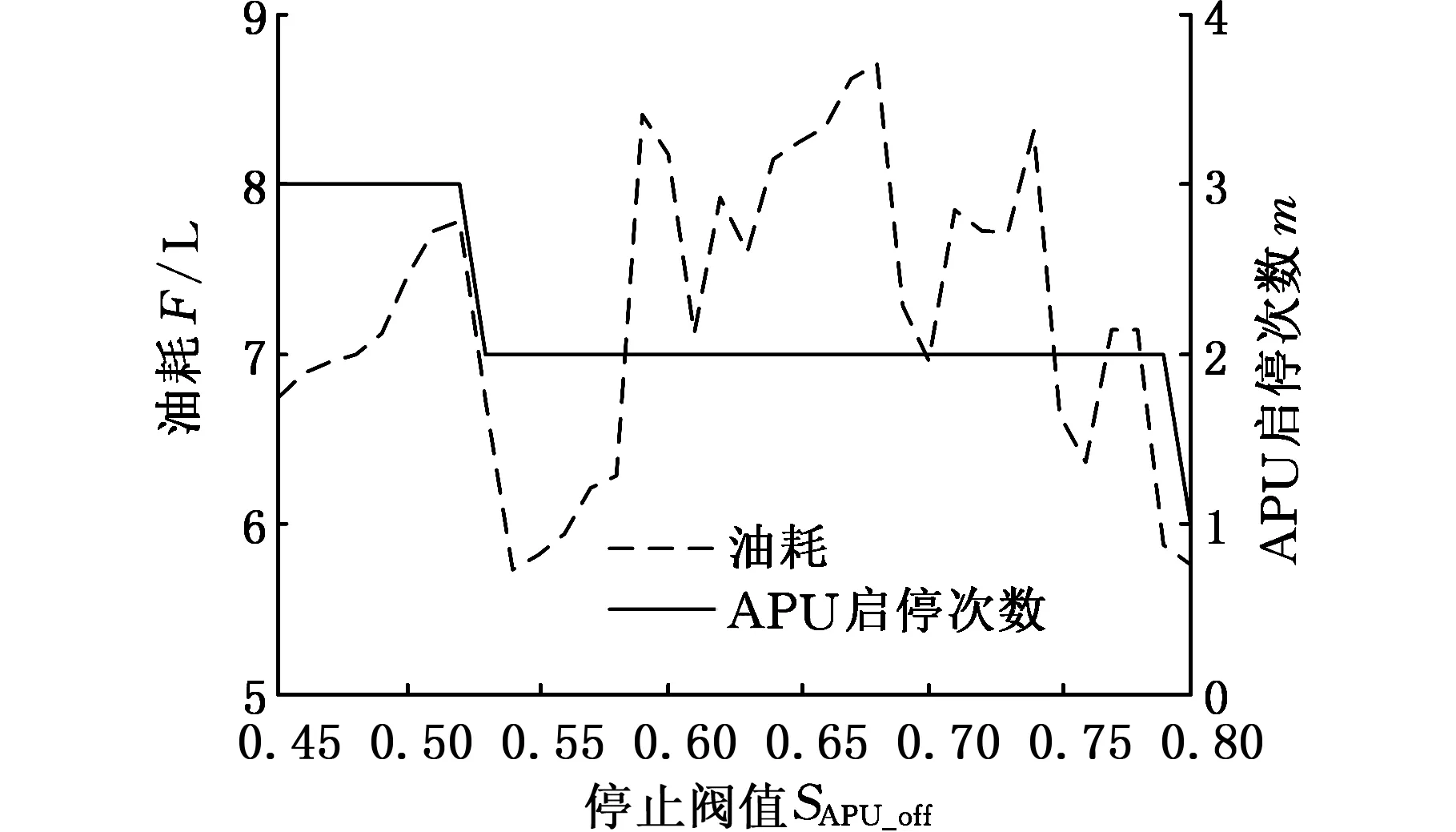
图8 APU启停次数和油耗随SAPU_off变化Fig.8 Change of APU start-stop times and fuel consumption with the change of SAPU_off

综合图8和图9可知，油耗和总的APU工作时间无线性关系。随SAPU_off变化，三个功率点工作时间此消彼长而导致油耗呈现不规则周期性变化。

图9 各负荷点工作时间随SAPU_off变化Fig.9 Change of working time of each load point with the change of SAPU_off

各负荷点固定，其对应的燃油消耗率固定，所以总的燃油消耗是各个负荷点的燃油消耗量对各负荷点工作时间的积分:

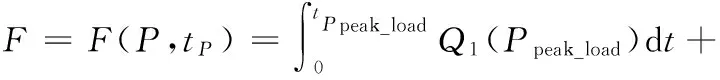
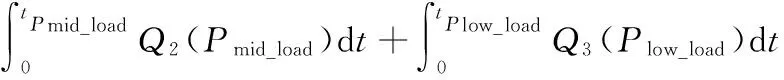
(4)

式中，Q1(Ppeak_load)、Q2(Pmid_load)、Q3(Plow_load)为各负荷点的燃油消耗率，L/s；F为总油耗，L。

由于图7和图9各负荷点的工作时间都是在特定里程200 km下得到的，故不断改变行驶里程，将得到不同的各负荷点工作时间随APU启停的变化数表，形成四维数表。

APU工作时间tP的计算公式为

(5)

其中，函数g(P,SAPU_start，L)如图7所示；h(P,SAPU_off，L)如图9所示。

总油耗F可表示为负荷P、行驶里程L、SAPU_start或SAPU_off的函数：

(6)

3.2 基于PSO不同里程APU启停控制策略优化

在上述优化模型的基础上，以油耗最小为目标，使用PSO算法优化APU启停控制参数。

PSO算法首先在可行域初始化一群粒子，每个粒子具有SAPU_start、SAPU_off两个维度；每个粒子也具有位置、速度、适应度值三个特征。其演化过程如图10所示，粒子对其行为(位置和速度)的修正通过综合考虑其自身因素(惯性或粒子对自身的认同度)、个体最优Pbest,id(认知部分)和全局最优Gbest,id(社会部分)。速度更新公式为

Vid(k+1)=wVid(k)+c1rand(Pbest,id-Xid(k))+
…+c2rand(Gbest,id-Xid(k))

(7)

位置更新公式为

Xid(k+1)=Xid(k)+Vid(k+1)

(8)

式中,Vid(k+1)为第k+1代粒子i的第d维分量的速度；Xid(k+1)为第k+1代粒子i的第d维分量的位置；rand是[0，1]区间的随机数;c1、c2分别为个体和社会学习因子；w为惯性权重。

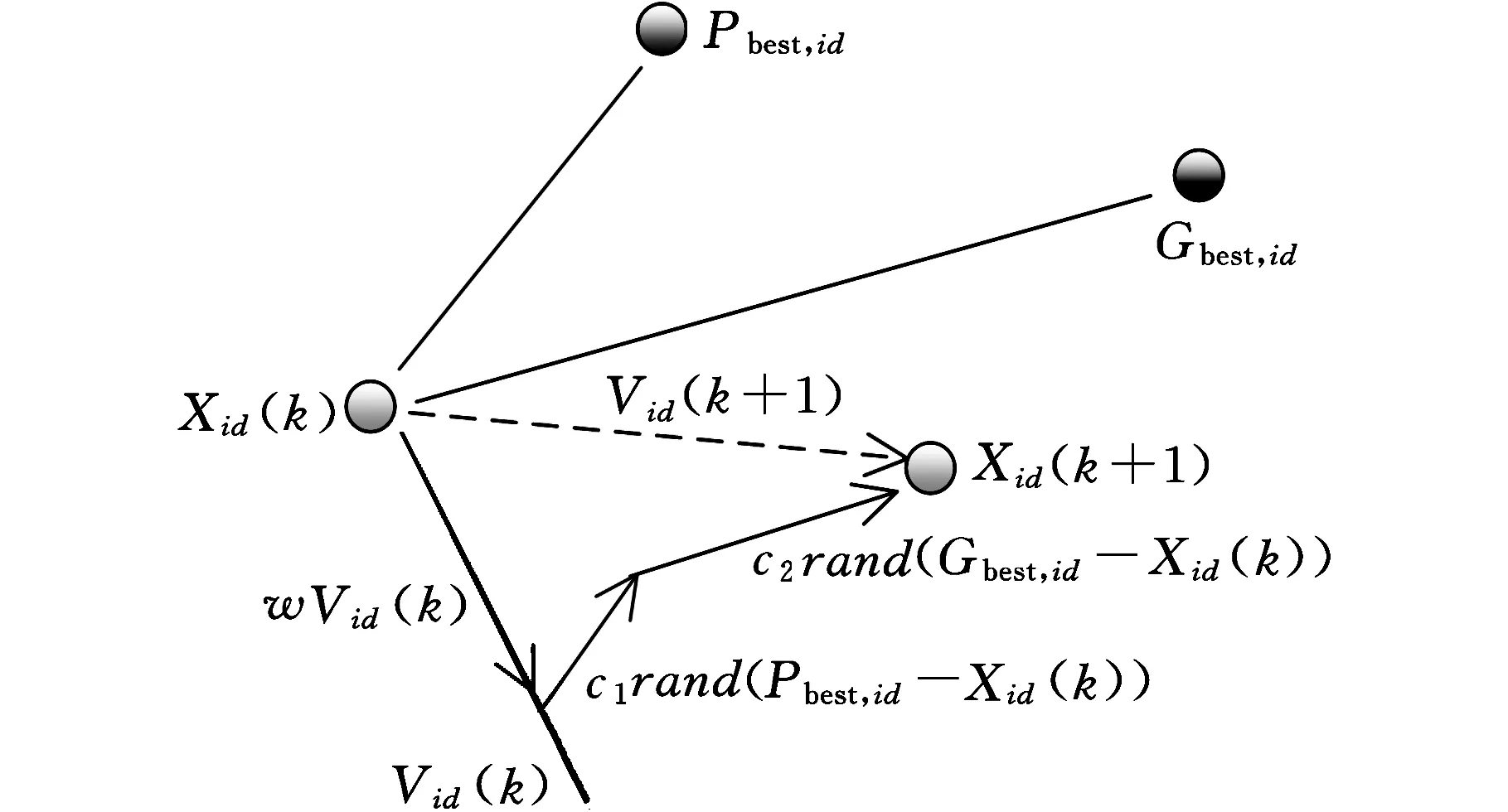
图10 APU启停控制参数PSO优化示意Fig.10 Sketch of optimization about parameters of APU start-stop

适应度函数(油耗)通过调用增程式电动汽车Simulink模型来计算，其值的好坏代表粒子优劣。约束条件为性能指标和电池循环寿命。性能指标转化为电池、电机和APU参数；动力电池的循环寿命和SOC使用范围息息相关，为了保证电池使用寿命，其工作范围为0.25～0.8。

VPSO算法设置为：迭代次数30，种群规模30，个体学习因子和社会学习因子c1=c2=1.4，惯性权重w初始值为0.9，随着粒子的修正，逐渐减为0.5，避免后期陷入局部最优。PSO迭代过程如图11所示。

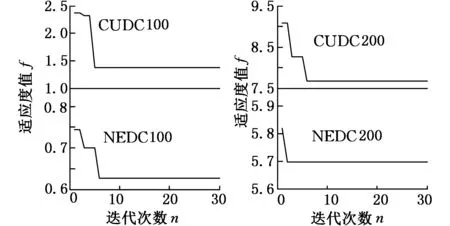
(a)100 km行驶里程 (b)200 km行驶里程图11 PSO迭代过程Fig.11 The iterative process of PSO

4 仿真实验验证及结果分析

采用NEDC和CUDC循环工况，分别以100 km和200 km进行验证，图12～图15所示为不同工况不同行驶里程优化前后的能量消耗，图16所示为优化前后油耗随里程变化情况，表4为优化前后参数对比。

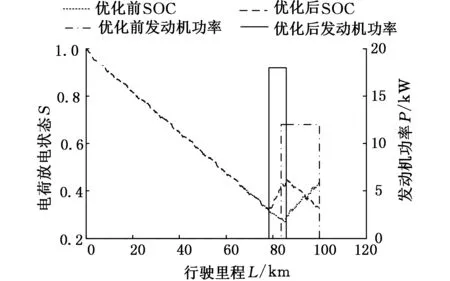
图12 CUDC工况100 km优化前后能量消耗Fig.12 Energy consumption before and after optimization in the condition of CUDC 100 km

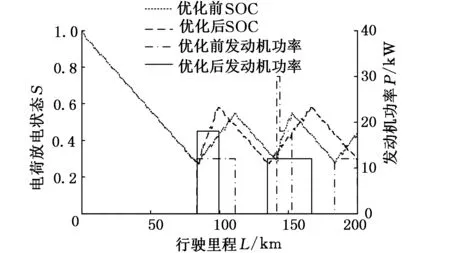
图13 CUDC工况200 km优化前后能量消耗Fig.13 Energy consumption before and after optimization in the condition of CUDC 200 km

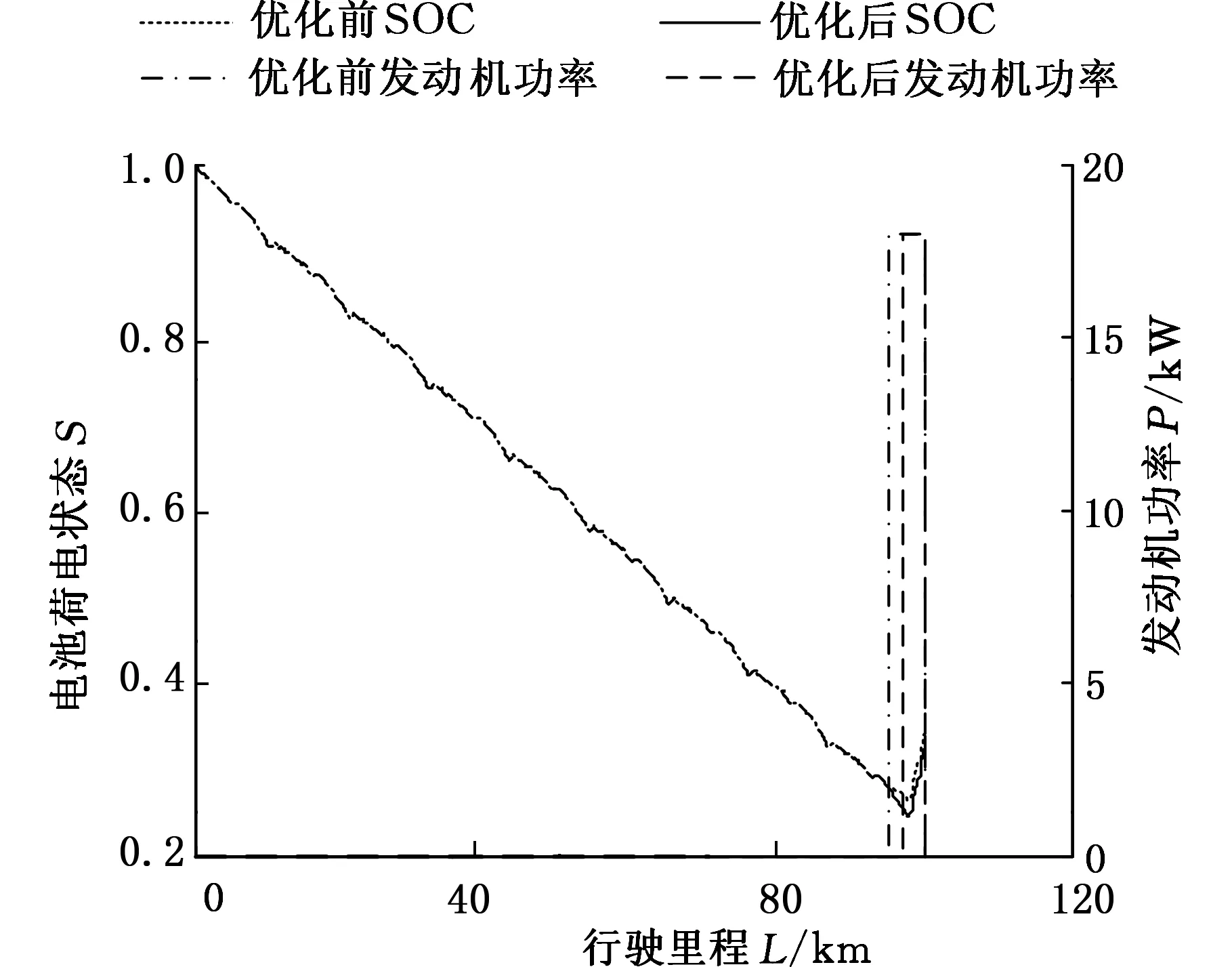
图14 NEDC工况100 km优化前后能量消耗Fig.14 Energy consumption before and after optimization in the condition of NEDC 100 km

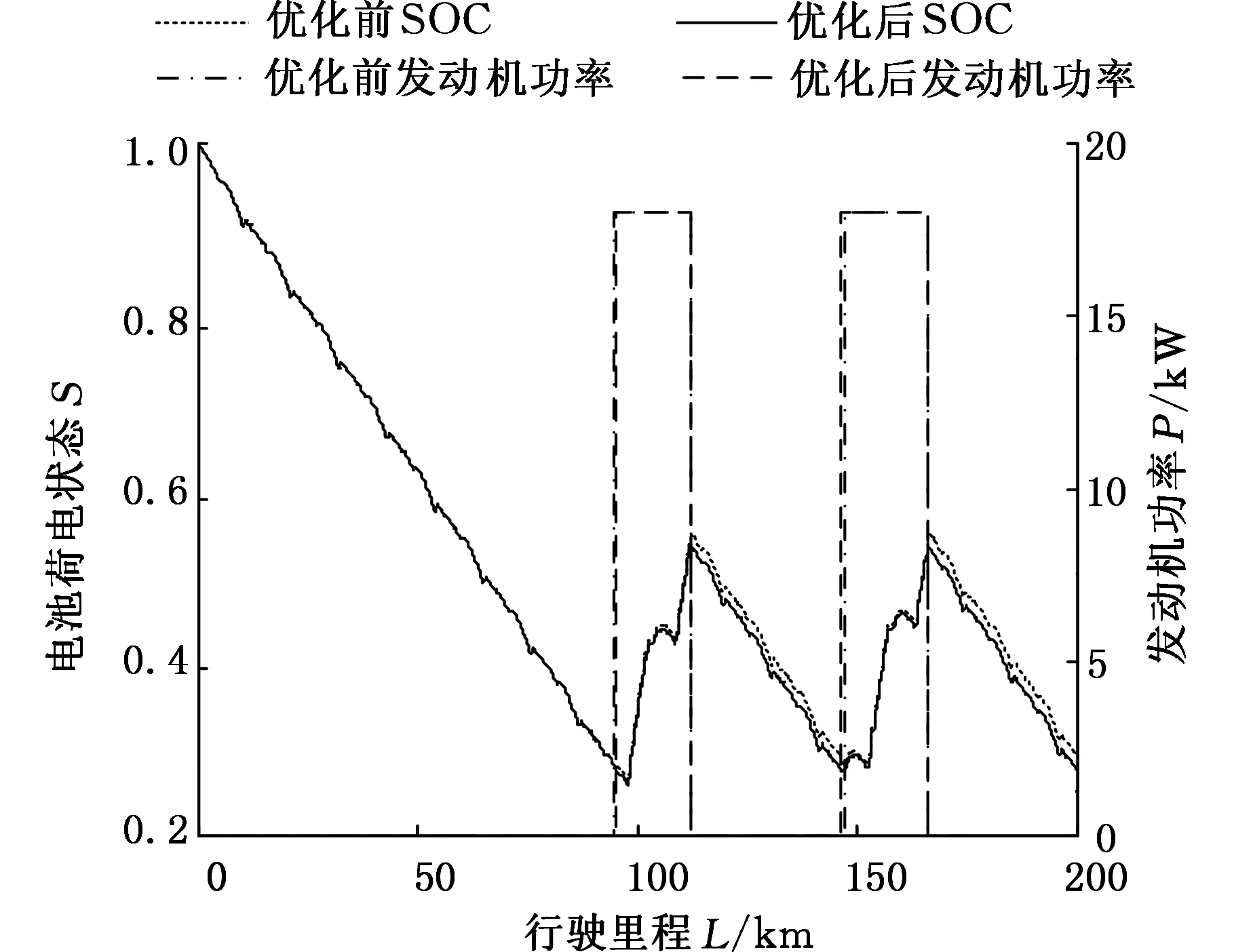
图15 NEDC工况200 km优化前后能量消耗Fig.15 Energy consumption before and after optimization in the condition of NEDC 200 km

CUDC工况100 km行驶里程(简称CUDC100)优化后，经济性提升最多，原因在于相比于优化前，提前开启APU，工作点由原来的低负荷点Plow_load变为Pmid_load中等负荷点，并提早关闭APU，此后APU未再开启直至里程终结。

CUDC工况200 km行驶里程(简称CUDC200)优化后，APU启停次数减少一次，运行工作点由原来的Ppeak_load、Pmid_load和Plow_load三工作点变为Pmid_load和Plow_load两工作点，燃油消耗减少14.54%。

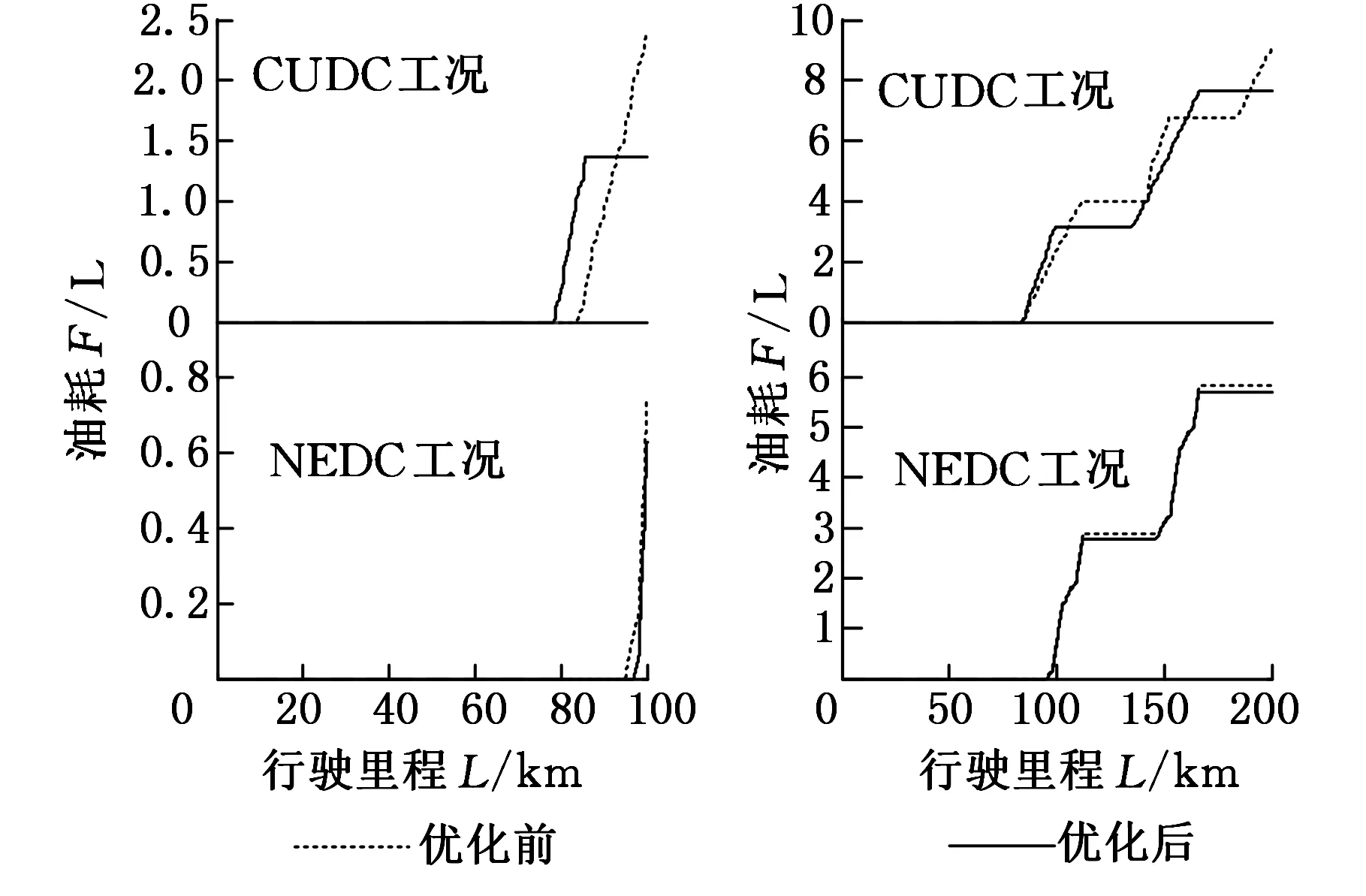
(a)100 km优化前后油耗 (b)200 km优化前后油耗图16 不同工况不同行驶里程优化前后油耗对比Fig.16 Fuel consumption contrast before and after optimization

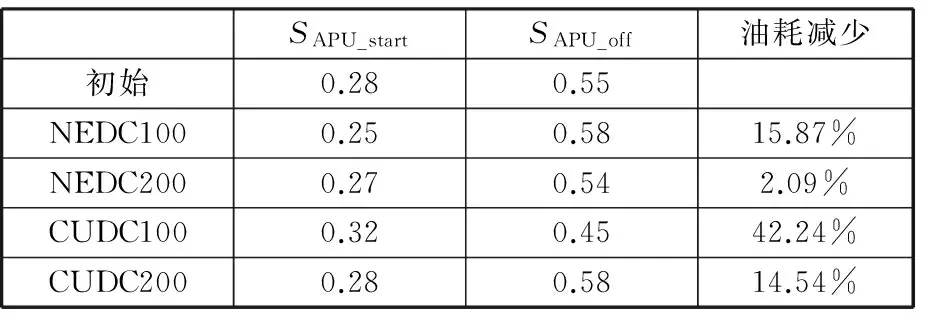
表4 优化前后参数对比Tab.4 Parameters contrast before and after optimization

NEDC工况100 km行驶里程(简称NEDC100)优化后，油耗减少15.87%，主要原因在于在允许范围内降低了SAPU_start，使得APU工作于Pmid_load时间缩短。APU延迟关闭不对油耗产生影响，在达到100 km时，优化前后均没有达到APU关闭阀值。

NEDC工况200 km行驶里程(简称NEDC200)优化前后燃油消耗略有减少，主要是初始参数是在此条件下优化得出的。

不同工况相同里程横向比较得出，尽管里程相同，不同工况将使得燃油消耗差异显著。100 kmCUDC工况比100 kmNEDC工况燃油消耗增加1.19倍(优化后)，200 kmCUDC工况比200 kmNEDC工况增加34.54%(优化后)。

细化行驶里程，得到里程与控制参数对应数表，在已知工况和行驶里程情况下，使得车辆VCU能够根据续航里程自适应改变控制参数。

5 结论

(1)针对某款增程式电动车，基于APU多点工作模式控制策略，以油耗最小为目标建立优化模型，以性能指标和电池寿命为约束，利用PSO算法对不同工况不同行驶里程下的APU启停控制参数进行优化，从而实现续航里程自适应APU启停控制。

(2)仿真实验结果表明所优化的控制参数效果明显，与初始参数相比，油耗在工况NEDC100、NEDC200、CUDC100、CUDC200分别减少了15.87%、2.09%、42.24%、14.54%。

(3)对于APU多点工作模式控制策略，油耗与APU总的工作时间和APU启停次数都无直接线性关系，而与每个工作点的时间都有关系，正是各个工作点的时间的此消彼长使得油耗呈现不规则周期性变化。同里程下减少油耗的方法为：单一负荷下，缩短APU工作时间；不同负荷情况下，延长中低负荷下工作时间，缩短高负荷下工作时间。

[1] RODRIGUES M, KING S, SCOTT D, et al. Advanced Energy Management Strategies for Range Extended Electric Vehicle[J]. SAE International,2015-26-0121.

[2] MILLO F, ROLANDO L, MALLAMO F, et al. Development of an Optimal Strategy for the Energy Management of a Range-extended Electric Vehicle with Additional Noise, Vibration and Harshness Constraints [J]. IMechE,2012,227(1):4-16.

[3] GUO Rong，MI Yi, CAO Chong. Subjective and Objective Evaluation of APU Start-stop NVH for a Range-extended Electric Vehicle[J].SAE International, 2015-01-0047.

[4] LI S G, SHARKH S M, WALSH F C, et al. Energy and Battery Management of a Plug-in Series Hybrid Electric Vehicle Using Fuzzy Logic [J]. IEEE Trans. Veh. Technol., 2011,60:3571-3585.

[5] 牛继高，周苏.增程式电动汽车增程器开/关机时刻的优化[J].汽车工程，2013,35(5)：418-423. NIU Jigao，ZHOU Su.On/off Timing Optimization for the Range-extender in Extended-Range Electric Vehicles[J]. Automotive Engineering,2013,35(5):418-423.

[6] LI Xianjing，LI Liguang，SUN Yongzheng，et al. Optimization of Control Strategy for Engine Start-stop in a Plug-in Series Hybrid Electric Vehicle [J].SAE International,2010-01-2214.

[7] CHEN B-C, WU Y-Y, TSAI H-C. Design and Analysis of Power Management Strategy for Range Extended Electric Vehicle Using Dynamic Programming [J]. Applied Energy,2014,113:1764-1774.

[8] HOU C, OUYANG M, XU L, et al. Approximate Pontryagin’s Minimum Principle Applied to the Energy Management of Plug-in Hybrid Electric Vehicles [J]. Applied Energy, 2014,115:174-89.

[9] GAO J-P, ZHU G-M,STRANGAS E G, et al. Equivalent Fuel Consumption Optimal Control of a Series Hybrid Electric Vehicle [J]. IMechE,2009,223:1003-1018.

[10] CHEN S-Y, HUNG Y-H, WU C-H, et al. Optimal Energy Management of a Hybrid Electric Powertrain System Using Improved Particle Swarm Optimization [J].Applied Energy,2015,160:132-145.

[11] WU X, CAO B, WEN J. Particle Swarm Optimization for Plugin Hybrid Electric Vehicle Control Strategy Parameter [C]// IEEE Vehicle Power and Propulsion Conference. Harbin,2008:3-5.

[12] WU J, ZHANG C H, CUI N X. PSO Algorithm-based Parameter Optimization for HEV and Its Control Strategy [J]. International Automot Tech., 2008,9(1):53-69.

[13] CHEN Zheng, XIA Bing, YOU Chenwen, et al. A Novel Energy Management Method for Series Plug-in Hybrid Electric Vehicles[J].Applied Energy,2015,145:172-179.

[14] WARREN V, ARUP K R, ROBERT G, et al. Electric Vehicle Range Prediction for Constant Speed Trip Using Multi-objective Optimization[J].Power Sources,2015, 275:435-446.

[15] GREWAL K S, DARNELL P M. Model-based EV Range Prediction for Electric Hybrid Vehicles[C]//Hybrid and Electric Vehicles Conference 2013. London, 2014:1-6.

(编辑 袁兴玲)

Optimization of APU Start-stop Control for Diverse Mileage Ranges

LIN Xinyou ZHANG Shaobo FENG Qigao
College of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, 350002

For a range-extended electric vehicle, a multi point energy management strategy was developed to meet different demands of power and energy. Then an optimization model of APU was formulated to achieve the target of minimum fuel consumption. In the constraints of performance index of range-extended electric vehicle and battery cycle life, optimization of control parameters of APU start-stop was performed by the SIMULINK model with diverse mileage ranges under different driving cycles to realize APU start-stop control for adaptive range. Compared with before optimization，the results show that fuel consumption is reduced by 15.87%/2.09%，42.24%/14.54% respectively corresponding to NEDC100/200,CUDC100/200. Based on energy consumption comparisons before and after optimization，the fuel economy may be obtained through reducing APU operation time under the condition of single loads and transferring operation time from peak loads to medium loads and low loads under the condition of multiple loads.

range-extended electric vehicle; mileage range; auxiliary power unit(APU); start-stop control

2015-12-07

国家自然科学基金资助项目(51505086)

U469.72

10.3969/j.issn.1004-132X.2017.01.019

林歆悠，男，1981年生。福州大学机械工程及自动化学院讲师、博士。主要研究方向为车辆动力传动与控制、混合动力电动汽车控制。张少博，男，1989年生。福州大学机械工程及自动化学院硕士研究生。冯其高，男，1989年生。福州大学机械工程及自动化学院硕士研究生。