基于有约束多目标进化算法的冷轧负荷分配分析

孙 浩 肖 宏 胡庆军1.燕山大学电气工程学院，秦皇岛，066002.燕山大学机械工程博士后流动站，秦皇岛，06600.燕山大学机械工程学院，秦皇岛，06600.天津电气科学研究院有限公司，天津，0001

基于有约束多目标进化算法的冷轧负荷分配分析

孙 浩1,2肖 宏3胡庆军4
1.燕山大学电气工程学院，秦皇岛，0660042.燕山大学机械工程博士后流动站，秦皇岛，0660043.燕山大学机械工程学院，秦皇岛，0660044.天津电气科学研究院有限公司，天津，300301

冷轧负荷分配问题可以抽象为一个有约束多目标优化问题。为解决此问题，提出了基于环境Pareto支配选择策略的有约束多目标进化算法。该算法更加客观地评价了两个不同解的优劣，利用优秀不可行解加速算法收敛。以等功率裕量、最小轧制能耗、最小综合打滑函数、末机架板形良好轧制力为优化目标，利用有约束多目标进化算法得到了4个目标函数之间的定量关系，使决策者不需要掌握复杂的轧制理论知识就可以直观地掌握轧制规律，并进一步说明了多目标策略在压下负荷分配中的必要性。

有约束多目标优化问题；约束处理技术；冷轧压下负荷分配；差分进化算法

0 引言

在冷连轧生产过程中，负荷分配直接关系到机组生产状态和产品质量。国内外科研人员通过建立不同的目标函数和约束条件来达到不同的生产目标[1]。单目标优化算法以其求解效率高、速度快等特点，在生产实际中得到了广泛应用。但轧制过程是一个多变量、时变性和强耦合的系统，根据单目标优化而来的结果很难满足各种要求，所以轧制过程的多目标优化问题被提出[2-4]。

轧制负荷分配本质是一个有约束多目标优化问题。国内外对无约束多目标优化问题的研究成果很多[5-6]，但对于约束处理技术的研究相对较少。王勇等[7]对当前基于进化算法的约束处理技术进行了较为详尽的概括。多目标约束处理技术大致分为三类：基于罚函数的约束处理技术、基于多目标算法的约束处理技术和基于排序的约束处理技术[8-10]。

在以往轧制负荷分配问题中，约束处理主要采用罚函数法。虽然罚函数法构造简单易于实现，但合理的惩罚系数难以确定。为克服这一缺点，本文提出基于环境Pareto支配选择策略的多目标进化算法。此策略更注重可行解与不可行解的客观比较，使得优秀不可行解在进化过程中得以保留，加快算法的收敛速度。

1 有约束多目标优化问题模型

以最小多目标优化问题为例，有约束多目标优化问题(multi-objective constrained optimizat-ion problem，MOCOP)可定义如下[11]：

min F(X)=(f1(X),f2(X),…,fk(X))s.t. gi(X)≤0 i=1,2,…,p
hj(X)=0 j=1,2,…,q

其中，F(X)为目标函数；X=(x1,x2,…,xn)∈Rn为n维决策向量;gi(X)、hj(X)分别为不等式约束和等式约束条件，满足约束条件的解空间S为上式的可行域。对于等式约束hj(X)=0可以设定容许误差δ>0，将它转变为如下不等式约束：

|hj(X)|≤δ

在后文问题的讨论中，仅考虑带有不等式约束的优化问题。

2 改进的有约束多目标进化算法

2.1 基于环境Pareto支配选择策略的提出

选择操作决定着算法的进化方向，是进化算法前进的动力，不同的选择策略会使进化种群向着不同的方向进化。利用这一生物学上的特性，对于有约束多目标问题，采用同样的处理策略。

在有约束多目标问题中，目前应用最广泛的是DEB等[12]提出的约束占优直接支配选择策略：

(1)两个个体相比较，如果一个个体为可行解，而另一个个体为不可行解，则选择可行解作为较优个体；

(2)两个个体相比较，当两个个体均为可行解，则选择非支配个体作为较优解，如果两个个体互不支配，则选择拥挤度较大的个体作为较优解；

(3)两个个体相比较，如果两个个体均为不可行解，则选择违反约束程度较小的个体作为较优个体。

通过以上描述不难看出，以上策略的选择结果更加倾向于可行解。不论在什么情况下可行解总是优于不可行解，这显然是不合理的。在有约束多目标问题中，决策空间被约束条件分为可行域和不可行域两部分。形象地说，如果将整个决策空间想象为一个大湖，那可行域就像是漂浮在湖中的数个孤岛，不可行域就是孤岛周围的湖水，想要登上这些孤岛和其中的“最佳解”，势必需要湖水中所携带的“信息”。如果仅仅依靠有限的可行解去寻找其中的最佳解集，其寻优效率势必低下，只有充分发掘不可行解的信息，两者相互配合才能更快更精准地寻找到全局最优解，所以，优秀的不可行解在寻优过程中所起的作用远远大于那些劣质的可行解。

在有约束多目标问题中，判断解的优劣不应只以约束作为唯一标准，应结合更多的环境信息。以进化种群作为计算整体，每一个个体均具有以下环境信息：违反约束程度、与约束边界的距离、拥挤度、支配关系。本文结合以上4个环境信息提出了一种环境Pareto支配选择策略：

(1)当一个个体为可行解，另一个个体为不可行解，如果可行解的边界距离小于不可行解的边界距离，则选择可行解作为较优个体，否则选择两个个体中的非支配个体，如果两个个体互不支配，则选择拥挤度较大的个体；

(2)当两个个体均为可行解时，选择非支配个体，如果两个个体互不支配，则选择拥挤度较大的个体；

(3)当两个个体均为不可行解时，选择非支配个体，如果两个个体互不支配，则选择违反约束程度较小的个体。

违反约束程度C及与约束边界距离D的计算公式为

式中，p为不等式约束个数；gj(xi)为第i个个体在不等式约束j下的值。

拥挤度W计算公式：

式中，k为目标函数个数;N为种群个体数;fj(1),fj(2),…,fj(N)为全部个体在目标函数j上从小到大的排列。

以上选择规则可用图1～图3表示。通过比较两种不同的选择策略可知，环境Pareto支配选择策略对规则(1)进行了较大的改动，不再以是否可行作为选择的唯一准则。由图1可知，环境Pareto支配选择策略中的规则(1)结合了其他环境因素，更加客观地评价了两个解之间的优劣，使得可行解与不可行解竞争时，优秀的不可行解得以胜出。对于有约束问题，这一选择机制更加合理，更加有利于优秀不可行解的保留，从而为变异、交叉等操作提供更有利的信息；环境Pareto支配选择策略规则(2)两者相同，仍然以支配关系作为选择标准；环境Pareto支配选择策略规则(3)增加了支配关系的比较，将其作为首要判断标准，使得不可行解也在一定程度上向着Pareto前沿进化，其次将约束程度作为最终判定指标，选择出违反约束程度较低的个体。

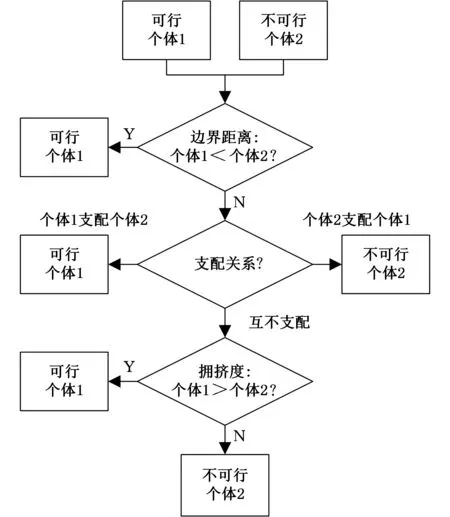
图1 环境Pareto支配选择策略规则(1)Fig.1 The first selection strategy of environmental Pareto dominance

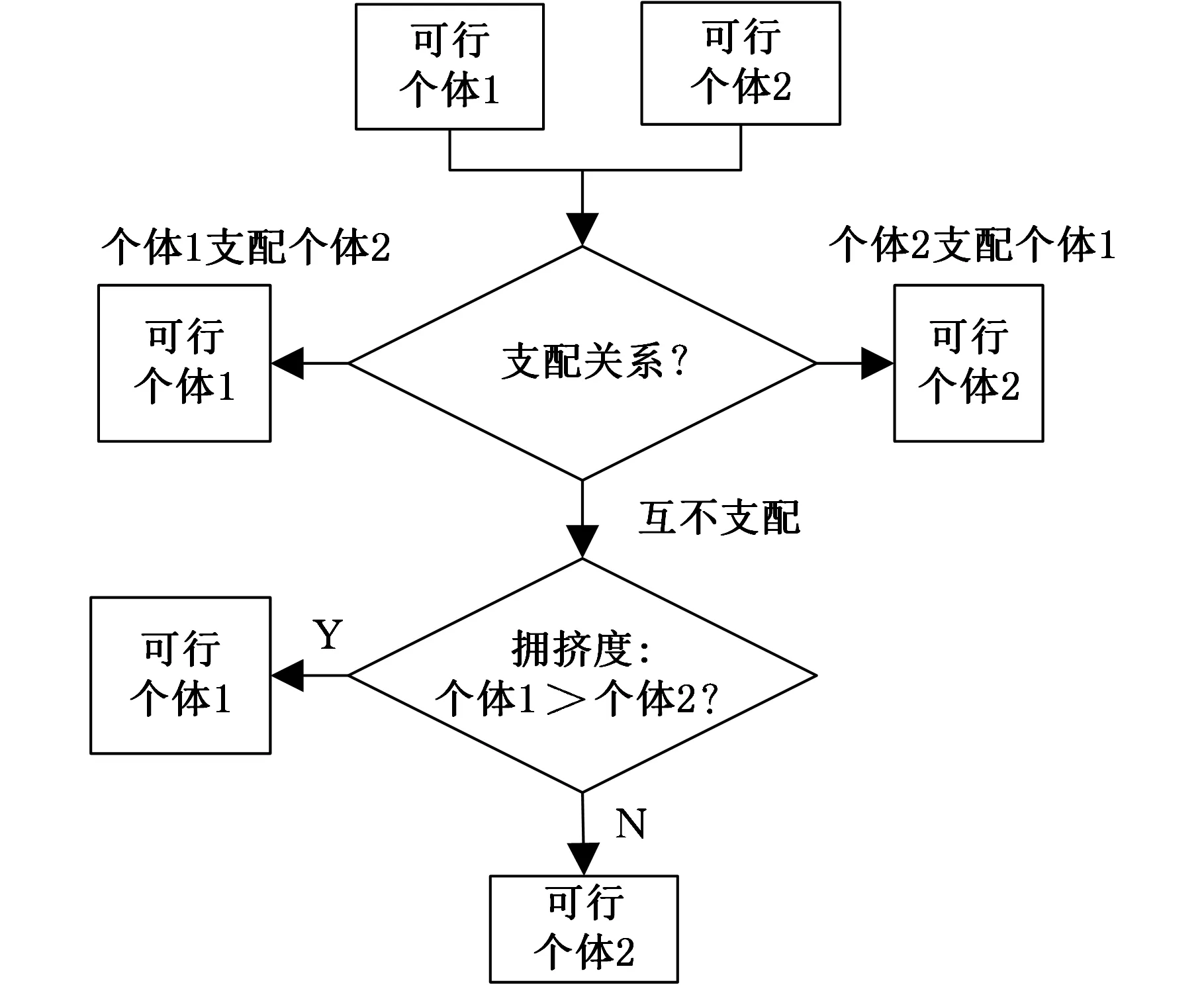
图2 环境Pareto支配选择策略规则(2)Fig.2 The second selection strategy of environmental Pareto dominance

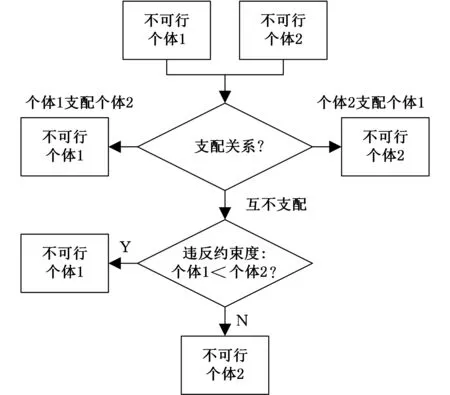
图3 环境Pareto支配选择策略规则(3)Fig.3 The third selection strategy of environmental Pareto dominance

2.2 改进的变异策略

有约束多目标问题有它自身的特点，最优Pareto前沿往往位于可行域与不可行域之间的边界。在进化计算中，优秀的不可行解同样不容忽视，它可以为进化过程提供有益的方向信息。为充分利用这一部分优秀不可行解，提出以下改进措施。

在进化过程中，外部不可行解集可能为空，所以定义以下两种情况：

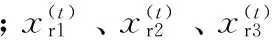
2.3 外部种群更新策略的改进

外部种群分为可行解集和不可行解集，设其最大容量分别为N1和N2(N1>N2)，具体更新方式如下。

可行解集的更新：将本代新产生的可行个体与可行解集结合为一个新的种群，选出其中的非支配个体，删除其他个体，如果个体数目小于N1则直接构成新的可行解集；如果数目大于N1则采用循环删除的方法删除拥挤度较小的个体[13]。

不可行解集的更新：设置平衡系数β2(0<β2<1)，将本代新产生的不可行个体与不可行解集结合为一个新的种群，选出其中的非支配个体，删除其他个体，如果个体数目小于N2，则直接构成新的不可行解集；如果个体数目介于N2与N2(1+β2)之间，则采用循环删除的方法删除拥挤度较小的个体；如果个体数目大于N2(1+β2)，则首先删除违反约束度较大的个体，使个体数目为N2(1+β2)，然后采用循环删除的方法删除拥挤度较小的个体。

2.4 算法流程

基于环境Pareto支配选择策略的有约束多目标差分进化算法的具体实现步骤如下：

(1)初始化，设定相关参数：种群大小P，可行解集大小N1，不可行解集大小N2，缩放因子F、变异概率PCR，变异策略选择概率β1，平衡系数β2，最大迭代次数G；

(2)随机产生大小为P的初始种群，计算其目标函数值和约束程度；

(3)依据2.3节生成可行解集与不可行解集；

(4)依据2.2节及基本差分进化算法[14]对本代个体进行变异及交叉操作；

(5)运用基于环境Pareto支配选择策略选择出下一代个体；

(6)更新可行解集与不可行解集；

(7)判断是否满足终止条件，若不满足转到步骤(4)，否则输出可行解集，即优化结果。

3 冷轧负荷分配分析

3.1 负荷分配计算流程

轧制负荷分配计算涉及一系列相关模型[15-17]，这些模型相互关联，相互影响。轧制负荷分配主要计算流程见图4。

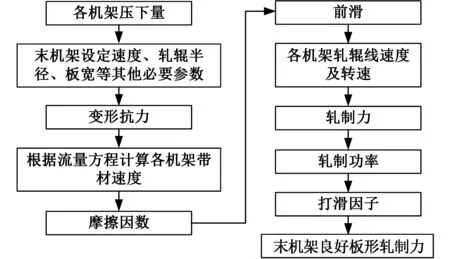
图4 负荷分配计算流程Fig.4 The flow chart of load dispatch

3.2 目标函数及约束条件的确定

为了充分发挥电机能力，一般选取等功率裕量为目标函数。为了保证末机架出口板形良好，其压下量只允许较小的值，所以不考虑末机架的功率裕量，其目标函数为

式中，Ni为i机架功率;kW；NHi为i机架额定功率，kW。

为了达到轧制过程中节能减排的目的，需制订最小轧制能耗目标函数。因为轧制能耗即为实际轧制功率与时间的乘积，所以本文采用最小轧制功率作为实际的目标函数：

其值越小，说明轧制能耗越低。

冷轧板形是评价板材质量的一个重要指标，所以建立末机架板形良好目标函数：

式中，KP为轧制力对辊系弯曲变形影响的横向刚度，kN/mm；Psh为保持良好板形所应有的轧制力，kN；Δ为原料凸度，mm；H0为原料厚度，mm；KF为弯辊力对辊系弯曲变形影响的横向刚度，kN/mm；h1为出口厚度，mm；Fw为弯辊力，kN；ω∑为综合初始辊型，mm；Eω为综合辊型影响系数。

为防止带材出现打滑现象，致使表面产生划痕，降低产品质量，各机架打滑因子应小于0.5，因此建立防打滑综合目标函数：

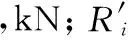
在负荷分配计算过程中，有一些必要的限制条件。计算结果不能超出设备和工艺要求的极值，定义以下约束条件。

设备因素约束条件：

Pi≤PiMNi≤NiMMi≤MiM

式中,Pi、Ni、Mi分别为轧制力、轧制功率和轧制力矩；PiM、NiM、MiM分别为设备允许的最大轧制力、最大轧制功率和最大轧制力矩。

工艺因素约束条件：

Tmin≤T≤Tmax

εmin≤ε≤εmax

nmin≤n≤nmax

式中,T、ε、n分别为张力、道次压下率和转速。

3.3 结果分析

仿真设定来料厚度5 mm，成品厚度1 mm，轧辊半径均为300 mm，张力由一机架入口到五机架出口依次为150 kN、130 kN、110 kN、90 kN、70 kN、50 kN，末机架出口板材速度8 m/s，板宽1250 mm，各个机架电机额定总功率均为18 000 kW，钢种Q235。

根据上述目标函数和约束条件，应用基于环境Pareto支配选择策略的有约束多目标差分进化算法对上述问题进行求解，可以得到4个目标函数之间的相互关系。由于4个目标函数之间的可视化显示难以表示，图5～图10给出了4个目标函数之间的两两关系，Pareto前沿以1000点描绘。图5～图10中，1表示等功率裕量极端点； 2表示最小能耗极端点；3表示综合打滑因子极端点； 4表示末机架最佳轧制力极端点；5表示选定的4个目标的均衡点。

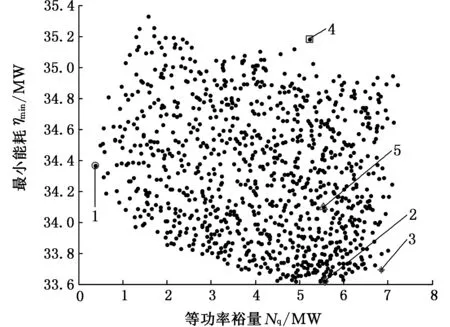
图5 功率裕量与最小能耗之间的关系Fig.5 The relationship between the power margin and minimum power

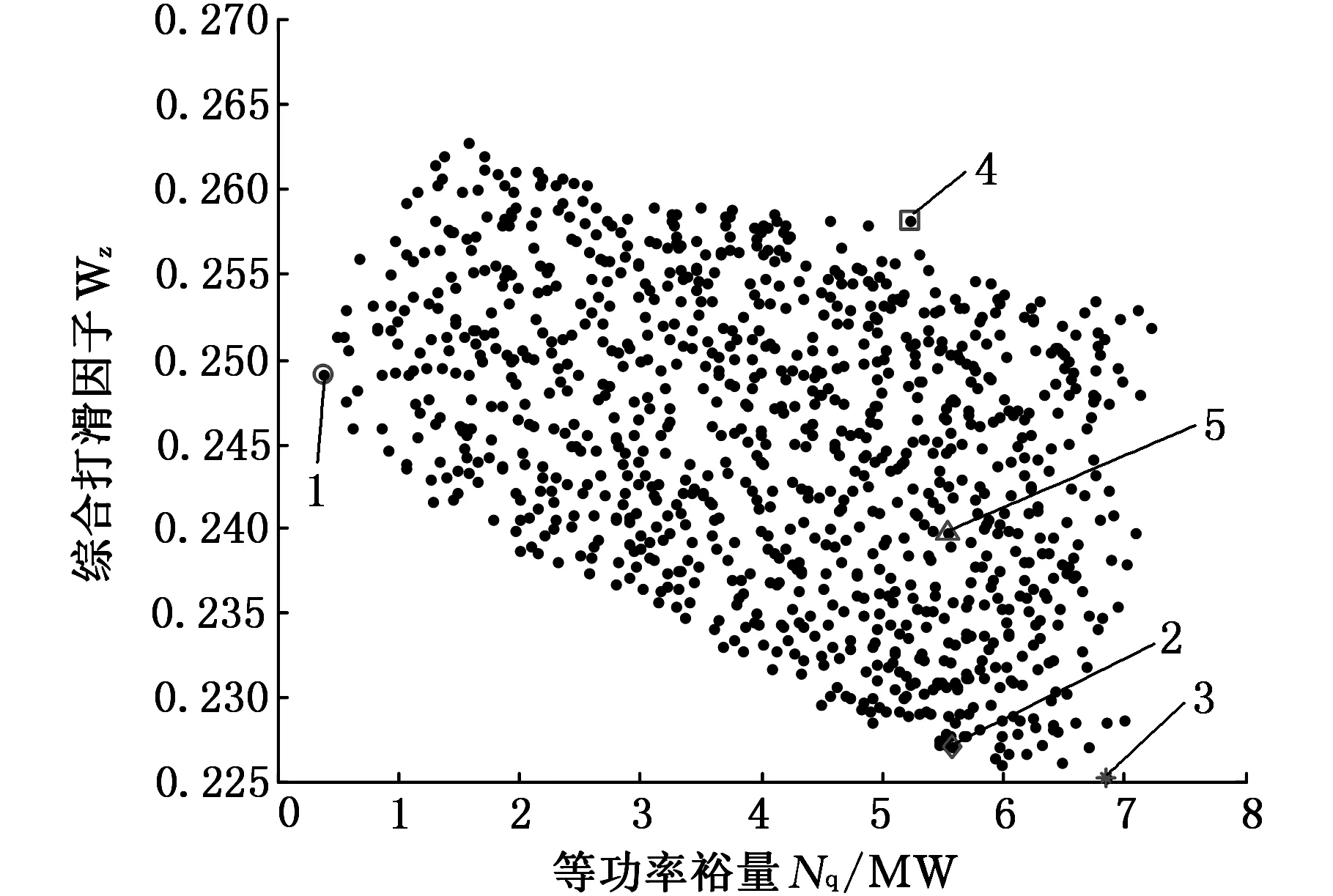
图6 功率裕量与打滑因子之间的关系Fig.6 The relationship between the power margin and slip factor

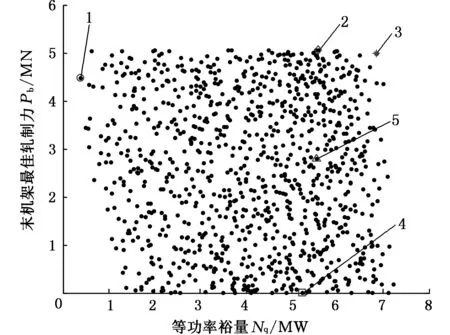
图7 功率裕量与板形良好轧制力之间的关系Fig.7 The relationship between the power margin and rolling force for quality shape

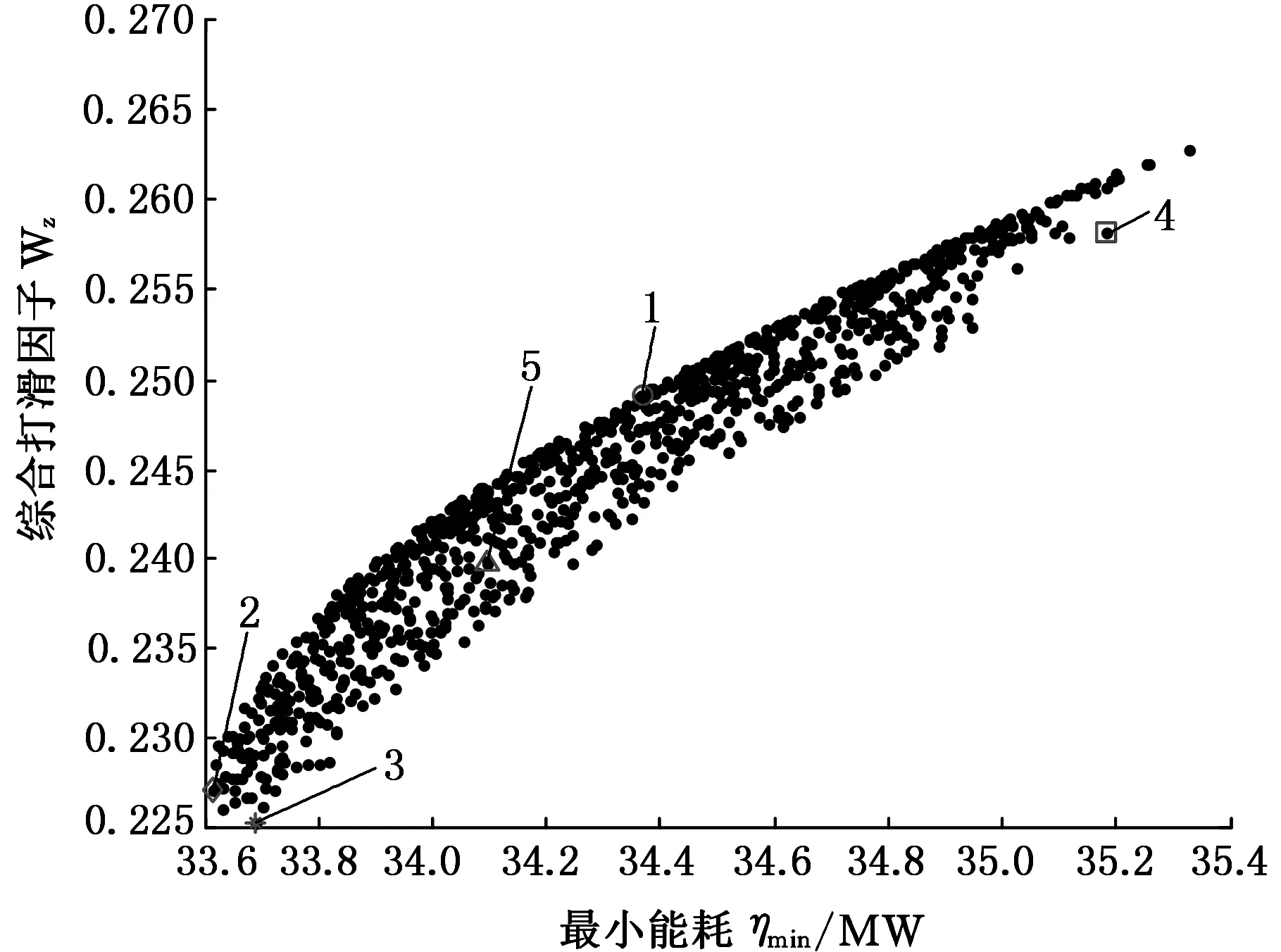
图8 最小能耗与打滑因子之间的关系Fig.8 The relationship between the minimum power and slip factor

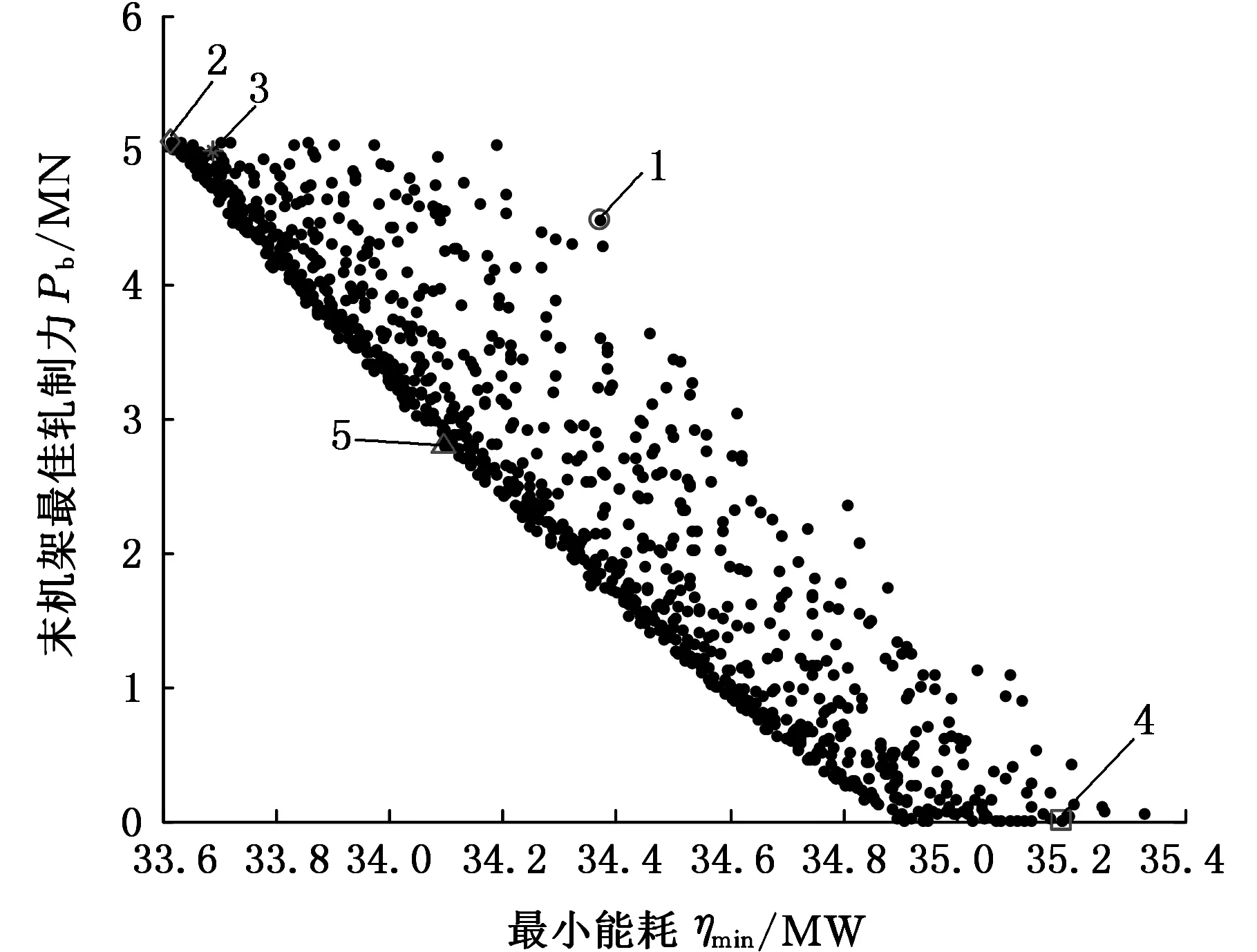
图9 最小能耗与板形良好轧制力之间的关系Fig.9 The relationship between the minimum power and rolling force for quality shape

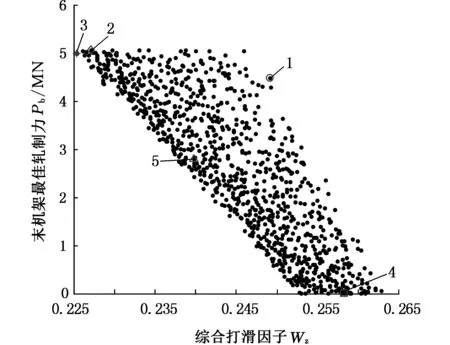
图10 打滑因子与板形良好轧制力之间的关系Fig.10 The relationship between the slip factor and rolling force for quality shape

在同时兼顾4个目标的情况下，由图5可知，等功率裕量和最小能耗两个目标之间呈四边形分布，两个目标函数均不可能同时达到最优，在这个近似的四边形区域内，当等功率裕量最小时最小功耗目标函数大约为3.44×104kW，能耗最大最小之间的差值为1800 kW，也就是说不论什么压下策略，轧制所消耗的能量最大值与最小值之差不超过1800 kW，这符合基本的能量守恒定律，即生产产品的单位能耗最小值是一定的，不可能无限减小，也不可能无限增大。

由图6可知，等功率裕量和打滑因子之间也呈四边形分布。当打滑因子目标函数最小时，功率裕量大概为6000 kW。若只考虑这两个目标函数，也不可能同时达到最优，在等功率裕量减小时，必然伴随着打滑因子的增大，如果产品更加偏重于板面质量，则要牺牲等功率裕量来尽可能减小打滑因子的值，反之亦然。理论上，只要保证各个机架的打滑因子小于0.5，则可显著降低打滑产生的概率。

由图7可知，等功率裕量和末机架板形良好轧制力之间没有明显的关系。等功率裕量只考虑了前4个机架的电机功率，而末机架板形良好只考虑了第五机架，前4个机架的功率平衡并不会对末机架轧制力产生较大的影响，所以，在优化结果的关系图中，可以很清楚地看出，两者之间的关系不明显。

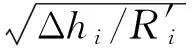
由图9可知，最小能耗和末机架板形良好轧制力之间呈现明显的负相关性，当能耗增大时，末机架板形良好轧制力将减小，直至为0。说明在增加能耗的情况下，有利于减小设定轧制力与期望轧制力之间的绝对差值，利于提高产品质量。

由图10可知，打滑因子与末机架良好板形轧制力之间也是负相关，也就是说必须在两者之间寻找一个平衡点，既不能使打滑概率超过期望值，也不能使末机架产生较大的板形偏差。

表1给出了当4个目标函数中每一个达到最优值和4个目标函数相对均衡时的计算参数。4个极端点及均衡点在Pareto前沿上的位置在图5～图10中已标记。由表1可知，当每一个目标函数达到最优时，可以看成是以这个目标函数为单目标问题的求解结果，结合图11～图14可知，当等功率裕量为最优时，轧制能耗高于两个策略而低于另一个，不能达到最佳节能，末机架板形良好轧制力也与预测需要的轧制力相差较大，5个机架的打滑因子分布也不均匀，第一机架的打滑因子明显略高，其他机架依次降低。当另外某一目标函数为最优时，相同的现象也会发生在其他目标函数上面。而选定的均衡点则综合考虑了4个目标函数之间的关系，使得各个目标函数值在满足生产条件的情况下达到相对最优。从优化结果中也可以看出，单目标优化不能兼顾其他，已经不能满足生产要求。而压下策略的制订必然要满足多种条件，以达到各方面生产工艺的要求。

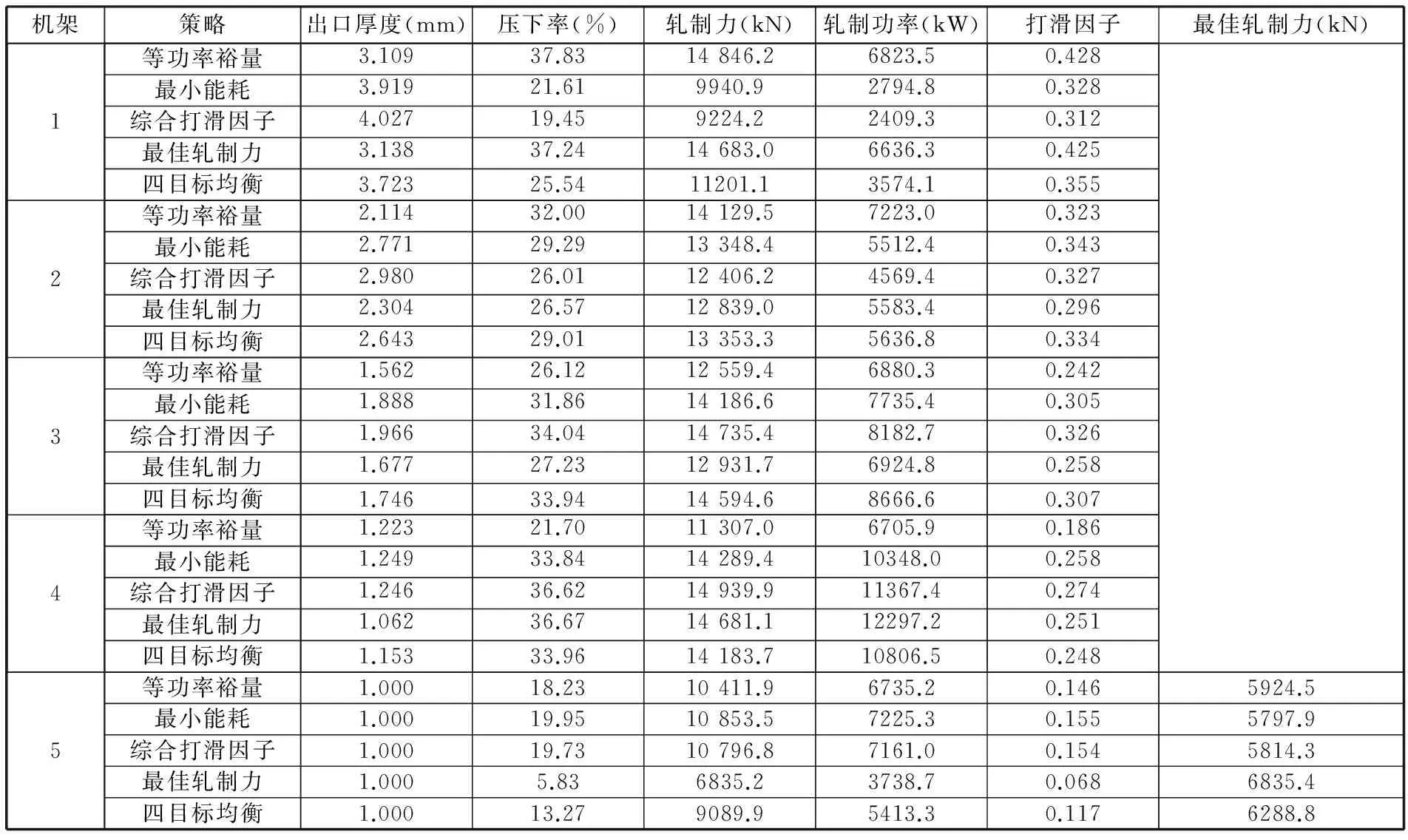
表1 不同策略下的计算参数Tab.1 The calculating parameters under different strategies

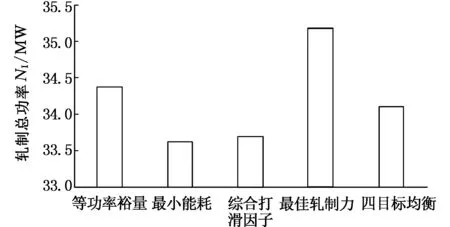
图11 不同极端策略下的轧制总功率比较Fig.11 The total power of rolling under different extreme strategy

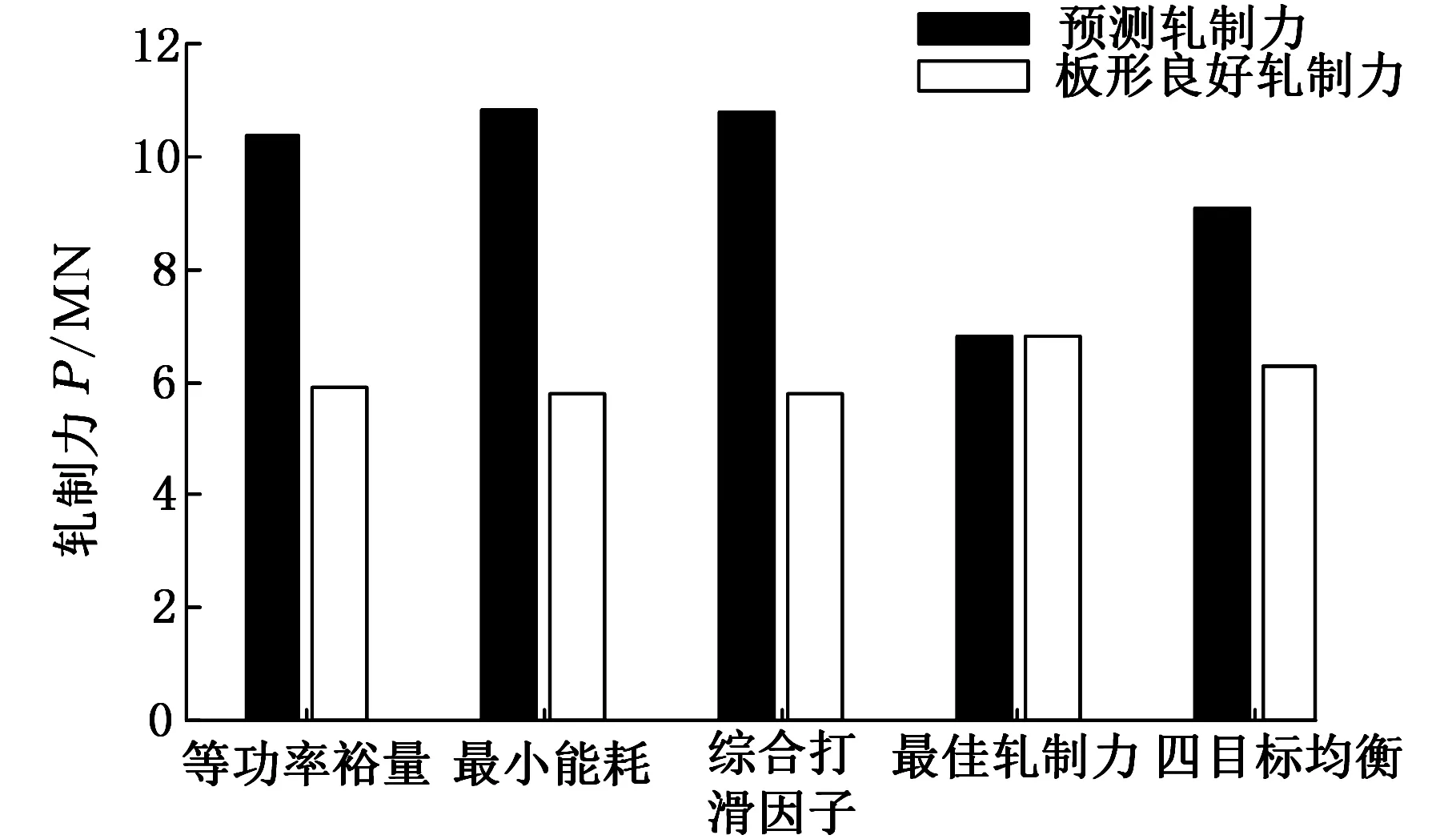
图12 不同极端策略下的末机架轧制力比较Fig.12 The rolling force of end stand under different extreme strategy

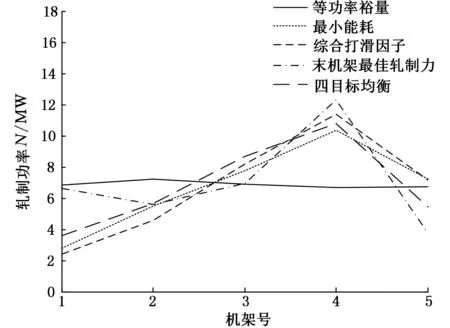
图13 不同极端策略下的各机架轧制功率比较Fig.13 The rolling power of each stand under different extreme strategy

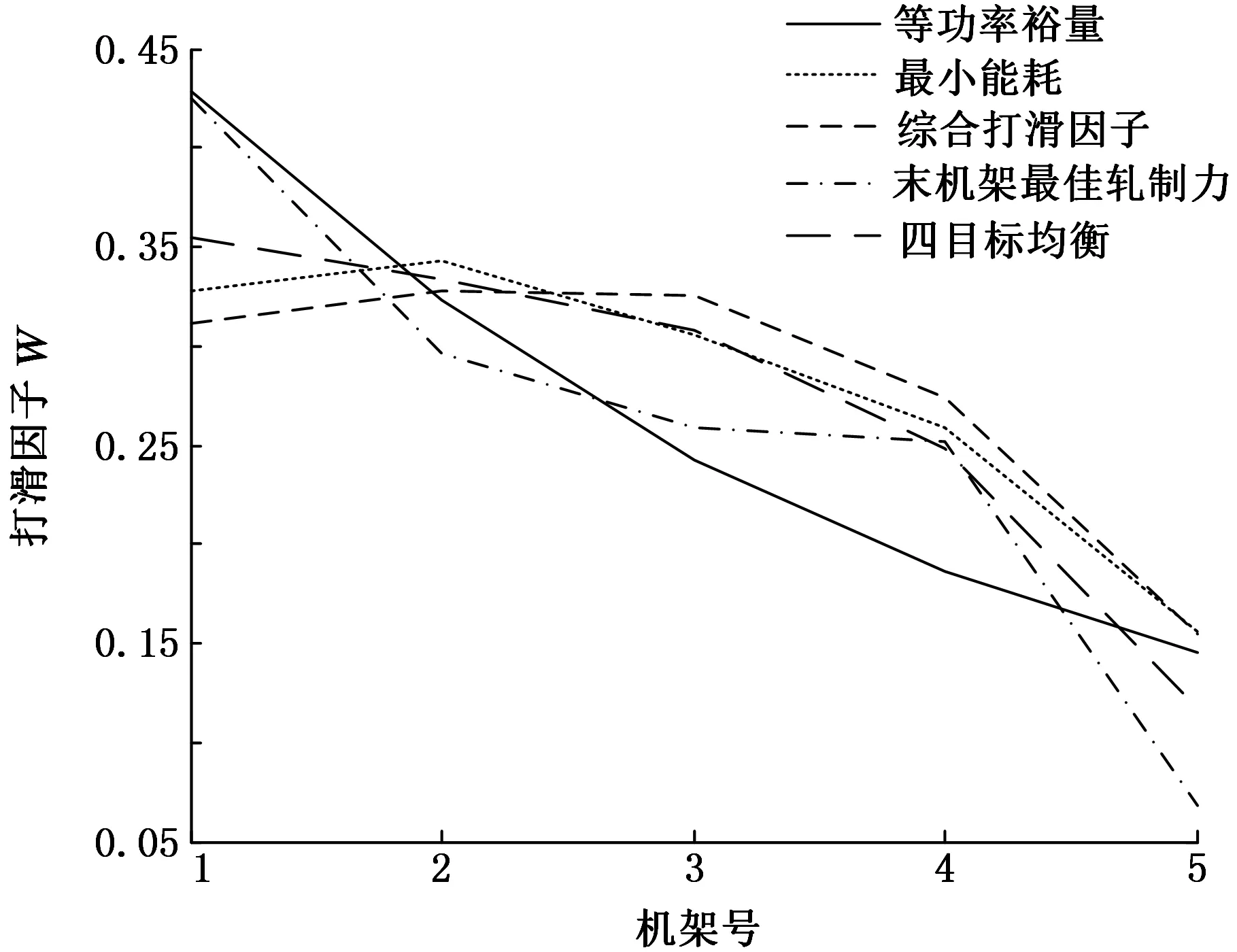
图14 不同极端策略下的各机架打滑因子比较Fig.14 The slip factor of each stand under different extreme strategy

通过基于环境Pareto支配选择策略的有约束多目标差分进化算法对4个目标函数进行求解，得到两两目标函数之间的定量关系，可以使得决策者不需要掌握复杂的轧制理论知识就可以很直观地掌握轧制规律。根据生产要求，通过对以上4个目标函数的综合分析，制订更加科学合理的压下策略。

4 结论

有约束多目标进化算法在科研及生产中有着广泛的应用，本文提出基于环境Pareto支配的选择策略，使得相较于劣质可行解的优秀不可行解得以进化到下一代，并且参与到变异当中，应用上述策略来处理多目标优化问题中的约束条件。该方法简单易行，不需考虑多余的参数。

轧制压下策略的多目标优化问题，不仅仅是一个优化求解问题，还可以从优化解集中形象地表示出各个目标函数之间的定量关系。通过这一最优解集，可以使得决策者不需要了解轧制理论就可以形象科学地认知到各个目标函数之间的定量关系，然后根据生产要求，制订不同的压下策略。

[1] YANG Jingming, ZHANG Qing, CHE Haijun, et al. Multi-objective Optimization for Tandem Cold Rolling Schedule[J]. Journal of Iron and Steel Research, International,2010,17(11):34-39.

[2] 李勇, 刘建昌, 王昱. 改进权重自适应 GA 及冷连轧轧制规程多目标优化[J]. 控制理论与应用,2009,26(6):687-693. LI Yong, LIU Jianchang, WANG Yu. An Improved Adaptive Weight Approach GA for Optimizing Multi-Objective Rolling Schedules in a Tandem Cold Rolling[J]. Control Theory and Applications,2009,26(6):687-693.

[3] 魏立新, 王利平, 马明明, 等. 基于改进多目标粒子群算法的冷连轧规程优化设计[J]. 中国机械工程,2015,26(9):1239-1259. WEI Lixin, WANG Liping, MA Mingming, et al. Optimization of Tandem Cold Rolling Schedule Based on Improved Muti-objective Particle Swarm Optimization Algorithm[J]. China Mechanical Engineering,2015,26(9):1239-1259.

[4] 魏立新, 李兴强, 刘泽, 等. 基于自适应遗传算法的冷连轧负荷分配优化[J]. 中国机械工程,2009,20(20):2506-2509. WEI Lixin, LI Xingqiang, LIU Ze, et al. Load Distribution Optimization in Tandem Cold Rolling Based on Adaptive Genetic Algorithm[J]. China Mechanical Engineering,2009,20(20):2506-2509.

[5] DEB K, JAIN H. An Evolutionary Many-objective Optimization Algorithm Using Reference-point-based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints[J]. Evolutionary Computation, IEEE Transactions on,2013,18(4):577-601.

[6] LI Hui, ZHANG Qingfu. Multiobjective Optimization Problems with Complicated Pareto Sets, MOEA/D and NSGA-Ⅱ[J]. Evolutionary Computation, IEEE Transactions on,2009,13(2):284-302.

[7] 王勇, 蔡自兴, 周育人, 等. 约束优化进化算法[J]. 软件学报,2009,20(1):11-29. WANG Yong, CAI Zixing, ZHOU Yuren, et al. Constrained Optimization Evolutionary Algorithms[J]. Journal of Software,2009,20(1):11-29.

[8] ZHANG Hao, ZHU Yunlong, ZHANG Dingyi. Self-adaptive Root Growth Model for Constrained Multi-objective Optimization[C]// Evolutionary Computation (CEC), 2013 IEEE Congress on. Cancun, Mexico,2013:2360-2367.

[9] 王建林, 吴佳欢, 张超然, 等. 基于自适应进化学习的约束多目标粒子群优化算法[J]. 控制与决策,2014,29(10):1765-1770. WANG Jianlin, WU Jiahuan, ZHANG Chaoran, et al. Constrained Multi-objective Particle Swarm Optimization Algorithm Based on Self-adaptive Evolutionary Learning[J]. Control and Decision,2014,29(10):1765-1770.

[10] 尚荣华, 焦李成, 胡朝旭, 等. 修正免疫克隆约束多目标优化算法[J]. 软件学报,2012,23(7):1773-1786. SHANG Ronghua, JIAO Licheng, HU Chaoxu, et al. Modified Immune Clonal Constrained Multi-objective Optimization Algorithm[J]. Journal of Software,2012,23(7):1773-1786.

[11] KARABOGA D, AKAY B. A Modified Artificial Bee Colony (ABC) Algorithm for Constrained Optimization Problems[J]. Applied Soft Computing,2011,11(3):3021-3031.[12] DEB K, PRATAP A, MEYARIVAN T. Constrained Test Problems for Multi-Objective Evolutionary Optimization[C]//Evolutionary Multi-criterion Optimization. Zwrich, Switzerland,2001:284-298.

[13] 罗辞勇, 陈民铀, 张聪誉. 采用循环拥挤排序策略的改进NSGA-Ⅱ算法[J]. 控制与决策,2010,(2):227-231. LUO Ciyong, CHEN Minyou, ZHANG Congyu. Improved NSGA-Ⅱ Algorithm with Circular Crowded Sorting[J]. Control and Decision,2010,(2):227-231.

[14] DAS S, SUGANTHAN P N. Differential Evolution: A Survey of the State-of-the-Art[J]. Evolutionary Computation, IEEE Transactions on,2011,15(1):4-31.

[15] 孙一康. 冷热轧板带轧机的模型与控制[M]. 北京: 冶金工业出版社,2010:30-36. SUN Yikang. Model and Control of Hot and Cold Strip Mill [M]. Beijing: Metallurgical Industry Press, 2010:30-36.

[16] 王军生, 金兰, 刘相华. 带钢冷连轧原理与过程控制[M]. 北京: 科学出版社, 2009. WANG Junsheng, BAI Jinlan, LIU Xianghua. Principle and Process Control of Cold Strip Rolling[M]. Beijing: Science Press, 2009.

[17] 白振华, 王骏飞. 冷连轧过程中实用摩擦系数模型及其影响因素的研究[J]. 中国机械工程,2005,16(21):1908-1911. BAI Zhenhua, WANG Junfei. Research on Practical Friction Coefficient and Its Influencing Factor in Cold Rolling Processes[J].China Mechanical Engineering,2005,16(21):1908-1911.

(编辑 袁兴玲)

Analysis for Load Distribution of Tandem Cold Rolling Based on Constrained Multi-objective Evolutionary Algorithm

SUN Hao1,2XIAO Hong3HU Qingjun4

1.School of Electrical Engineering,Yanshan University, Qinhuangdao，Hebei，066004 2.Post-Doctoral Stations of Mechanical Engineering, Yanshan University, Qinhuangdao，Hebei，066004 3.School of Mechanical Engineering, Yanshan University，Qinhuangdao，Hebei，066004 4.Research Institute of Electric Science Co.，Ltd.，Tianjin，300301

The load distribution of tandem cold rolling might be abstracted as a constrained multi-objective optimization problem. To solve this problem, an evolution algorithm was proposed based on environmental Pareto dominated selection strategy. The algorithm which accelerated the convergence speed by excellent infeasible solutions gave a more objective evaluation of the different solutions. Taking the power margin, minimum total rolling energy consumption, minimum slip factor and the best rolling force at last rack as optimizing criterion, the quantitative relationship among four objective functions was obtained by the constrained multi-objective evolutionary algorithm, which made decision-maker grasp the rules of rolling intuitively without proficient in complex rolling theory knowledge. And the necessity of the multi-objective strategy in the load distribution of tandem cold rolling was illustrated.

constrained multi-objective optimization problem； constraint-handling technique； the load distribution of tandem cold rolling； differential evolution algorithm

2016-03-09

燕山大学博士基金资助项目(B963)；国家自然科学基金委员会与宝钢集团有限公司联合资助项目(U1260203)；河北省自然科学基金资助项目(F2016203249)；河北省高等学校创新团队领军人才培育计划资助项目(LJRC013)；国家冷轧板带装备及工艺工程技术研究中心开放课题资助项目(2012005)

TG335

10.3969/j.issn.1004-132X.2017.01.016

孙 浩，男，1985年生。燕山大学电气工程学院讲师、博士。主要研究方向为轧制过程自动控制及多目标进化算法。E-mail:sunhao@ysu.edu.cn。肖 宏，男，1962年生。燕山大学机械工程学院教授、博士研究生导师。胡庆军，男，1982年生。天津电气科学研究院有限公司系统工程一公司副总经理。